В этой подборке собрано 10 реализаций математических задач, которые с легкостью решаются программно. Сможете ли решить все самостоятельно?
Часть математических задач, которые мы разобрали, могут быть достаточно простыми. Но в каждой из них найдутся элегантные математические приемы, реализованные в виде программного кода.
Кратчайшее расстояние между точкой и кругом
Дан радиус круга, координаты его центра и точка. Нужно найти кратчайшее расстояние между точкой и кругом.
Дано: x1 = 4, y1 = 6, x2 = 35, y2 = 42, r = 5 Результат: 42.5079 Дано: x1 = 0, y1 = 0, x2 = 5, y2 = 12, r = 3 Результат: 10
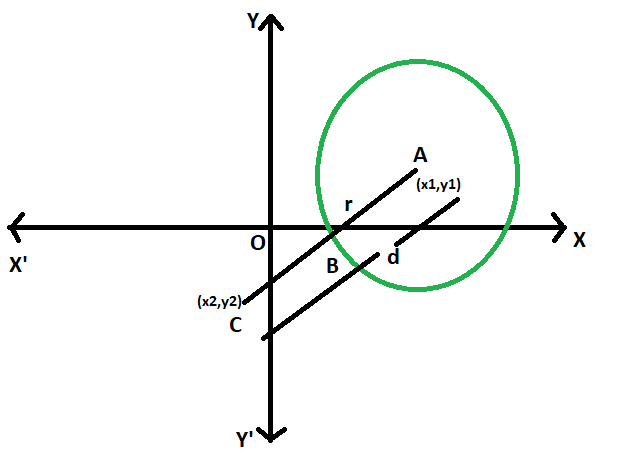
Обозначим радиус r. Координаты центра (x1, y1), точки (x2, y2). Пусть расстояние между точкой и кругом d. Тогда отрезок AC пересекает круг в точке B, кратчайшее расстояние отсюда будет равно отрезку BC, то есть (d-r). А d выражается как sqrt((x2 - x1)^2 - (y2 - y1)^2).
def dist(x1, y1, x2, y2, r):
result = ((x2-x1)**2 + (y2-y1)**2)**0.5 - r
return result
if __name__ == '__main__':
example = 4, 6, 35, 42, 5
print(dist(*example))
Кратчайшее расстояние от центра круга до хорды
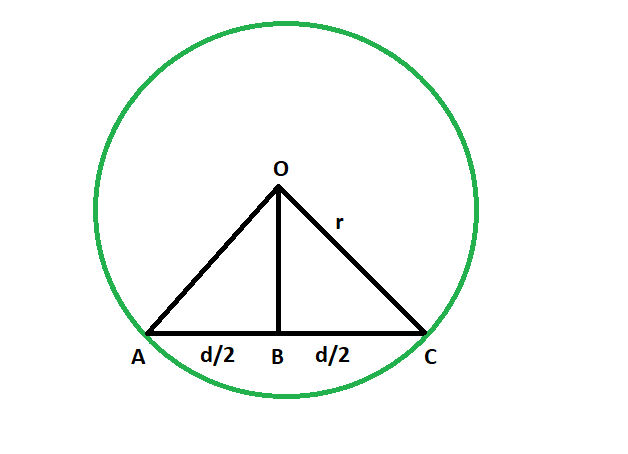
Дан радиус круга и длина его хорды. Нужно найти расстояние от центра круга до дуги.
Вход: r = 4, d = 3 Результат: 3.7081 Вход: r = 9.8, d = 7.3 Результат: 9.09492
def dist(radius, chord):
result = (radius**2 - chord**2/4)**0.5
return result
if __name__ == '__main__':
example = 4, 3
print(dist(*example))
Радиус круга через длину и ширину его дуги
Дана дуга с высотой и шириной. Нужно найти радиус этого круга.
Вход: d = 4, h = 1 Результат: радиус круга = 2.5 Вход: d = 14, h = 8 Результат: радиус круга = 7.0625
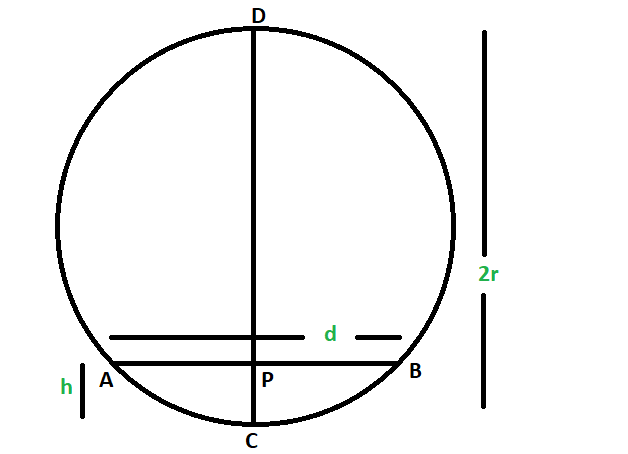
Обозначим радиус как r, а длину и ширину дуги – h и w соответственно. Тогда диаметр DC рассекает хорду AB на две половины, то есть на d/2. А хорда, в свою очередь, делит диаметр на отрезки h и 2r-h. Воспользовавшись теоремой о пересекающихся хордах, можно рассчитать радиус через равенство h*(2r-h) = (d/2)^2.
def radius(width, height):
result = width**2 / 8*height + height/2
return result
if __name__ == '__main__':
example = 4, 1
print(radius(*example))
Определить количество квадратов, которые пересекает линия
Задана линия через две точки: (x1, y1) и (x2, y2). Нужно определить, через сколько квадратов (размером 1 на 1) пройдет эта линия.
Вход: (x1 = 1, y1 = 1), (x2 = 4, y2 = 3) Результат: 4 (на рисунке ниже линия пересекает 4 квадрата) Вход: (x1 = 0, y1 = 0), (x2 = 2, y2 = 2) Результат: 2
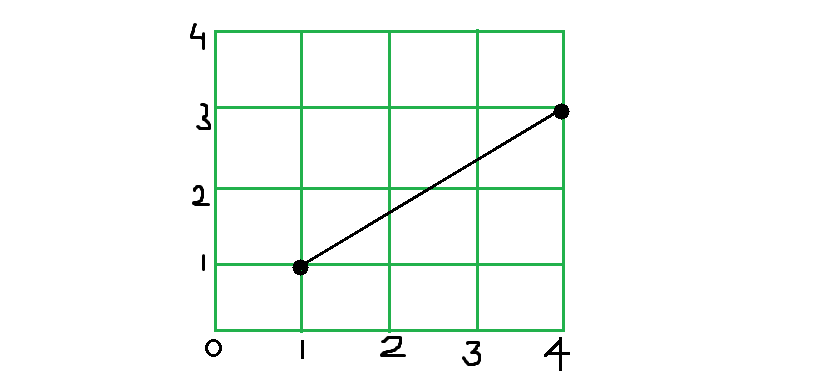
Линия образует прямоугольник, ширина и высота которого в квадратах – M и N соответственно (она является диагональю). Предположим, что M и N не имеют общего делителя, отличного от 1. Тогда линия пересечет M - 1 квадрат по горизонтали и N - 1 квадрат по вертикали (случай 1 и 2 на рисунке ниже). В сумме, учитывая начальный квадрат: 1+ (N-1) + (M-1) = N + M - 1.
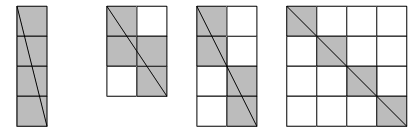
Допустим, N и M имеют наибольший общий делитель, отличный от 1. Обозначим его как q. Отсюда следует, что N/q и M/q не имеют общего делителя. Это значит, что мы можем разделить сетку на q меньших прямоугольников и считать их так же, как в первом случае: N/q + M/q - 1 для каждого. В общем случае: N + M - q. Это и есть конечная формула.
from math import gcd
def number_of_crossed_squares(x1, y1, x2, y2):
dx = abs(x2 - x1)
dy = abs(y2 - y1)
result = dx + dy - gcd(dx, dy) # gcd - встроенная функция поиска наибольшего общего делителя
return result
if __name__ == '__main__':
example = 1, 1, 4, 3
print(number_of_crossed_squares(*example))
Посчитать количество шагов из точки (0, 0) в точку (x, y) зигзагом
Даны координаты (x, y). Нужно посчитать количество шагов, которые нужно проделать из точки (0, 0) в точку с координатами.
Вход: x = 4, y = 4 Результат: 8 На рисунке ниже этот вариант разобран визуально Вход: x = 4, y = 3 Результат: 9 Вход: x = 2, y = 1 Результат: 5
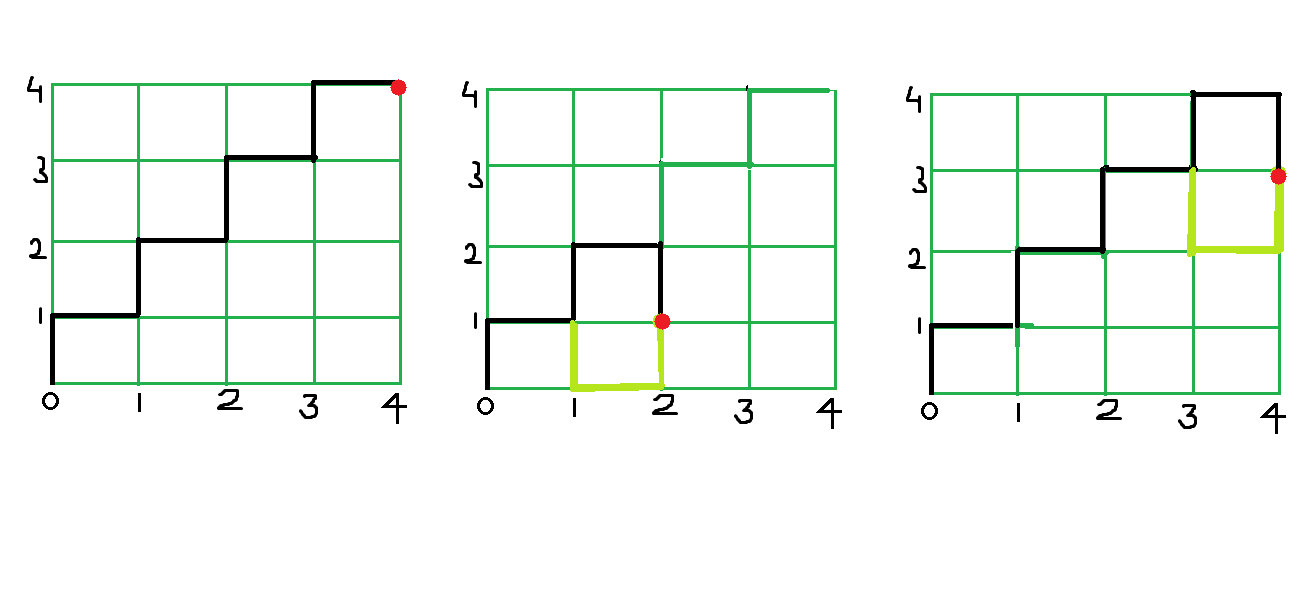Здесь два варианта:
-
- Если x меньше y, то ответ будет равен x + y + 2*((y-x)/2).
- Если x больше или равен y – x + y + 2*(((x-y)+1)/2).
def count_steps(x, y):
if x < y:
return x + y + 2 * ((y - x) // 2)
else:
return x + y + 2 * (((x - y) + 1) // 2)
if __name__ == '__main__':
x, y = 4, 3
print(count_steps(x, y))
Найти простое число палиндром, которое следует за данным
Дано положительное целое число N, такое, что 1 <= N <= 10^9. Найти самое маленькое простое число-палиндром, которое больше N. Из всех математических задач данной статьи, эта затрагивает самые красивые элементы математики: палиндромы и простые числа.
Вход: 8 Результат: 11 Вход: 7000000000 Результат: 10000500001
Простым и интуитивным решением будет идти по всем N+1 и делать проверки на простое число и палиндром. Но при решении подобных математических задач просто – не значит эффективно.
Предположим, что наше число R – искомое. Так как это палиндром, то первая половина его числа может представить его в 2 вариациях. Возьмем K как первую половину. Если K = 123, то R может быть и 123321, и 12321. Так что можно взять K до 10^5, составлять из этого числа палиндром R и проверять его, простое оно или нет.
import math
# Функция, которая проверяет, является ли число простым
def is_prime(number):
return number > 1 and all(number % divider for divider in range(2, int(math.sqrt(number)) + 1))
def next_prime_palindrome(n):
for k in range(1, 10**5+1):
# проверка на палиндром нечетной длины
s = str(k)
x = int(s + s[-2::-1]) # пример: s = '1234', x = int('1234321')
if x >= n and is_prime(x):
return x
# проверка на палиндром четной длины
s = str(k)
x = int(s + s[-1::-1]) # пример: s = '1234' to x = int('12344321')
if x >= n and is_prime(x):
return x
if __name__ == '__main__':
test = 7000000
print(next_prime_palindrome(test))
Количество пар чисел из N натуральных, чья сумма делится на K
Простым решением, наверное, будет цикл по всем парам и вычисление делимости их суммы на K. Так? Или же нет?
На самом деле можно использовать хеширование, которое заметно упростит задачу.
Вход: N = 10, K = 5 Результат: 9 Все пары, чья сумма делится на 5: (1, 4), (1, 9), (6, 4), (6, 9), (2, 3), (2, 8), (3, 7), (7, 8) и (5, 10) Вход: N = 7, K = 3 Результат: 7 Все пары, чья сумма делится на 3: (1, 2), (1, 5), (2, 4), (2, 7), (3, 6), (4, 5) и (5, 7).
def find_pair_count(n, k):
count = 0
# Создаём массив размером k
reminders = [0 for _ in range(k)]
# Первым элементом массива является количество натуральных чисел, которые при делении
# на K в остатке дают 0. Сам 0 при этом мы не считаем, так как это не натуральное число.
reminders[0] = n // k
# Заполняем массив количеством целых чисел, остаток от деления на K, который равен индексу
for i in range(1, k):
reminders[i] = (n - i) // k + 1
# Проверяем, является ли k четным
if k % 2 == 0:
# Считаем пары, где оба числа делятся на K
count += (reminders[0] * (reminders[0] - 1)) // 2
# Считаем пары, где первое число - остаток от деления, а второе - это разность K и этого остатка
for i in range(1, k // 2):
count += reminders[i] * reminders[k - i]
# Считаем пары, где оба остатка равны K / 2
count += (reminders[k // 2] * (reminders[k // 2] - 1)) // 2
else:
# Считаем пары, где оба числа делятся на K
count += (reminders[0] * (reminders[0] - 1)) // 2
# Считаем пары, где первое число - остаток от деления, а второе - это разность K и этого остатка
for i in range(1, k // 2 + 1):
count += reminders[i] * reminders[k - i]
return count
if __name__ == '__main__':
# Print the count of pairs
print(find_pair_count(10, 4))
Проверить, можно ли выразить число как сумму двух избыточных чисел
Число является избыточным, если сумма его положительных делителей, отличных от него самого, превышает это число.
Вход: N = 24 Результат: 12, 12 Вход: N = 5 Результат: -1 (невозможно)
from math import sqrt
def abundant(limit):
abundant_numbers_set = set()
for i in range(1, limit):
sum_of_divisors = 1
for j in range(2, int(sqrt(i)) + 1):
if i % j == 0:
sum_of_divisors += j
if i / j != j:
sum_of_divisors += i // j
if sum_of_divisors > i:
abundant_numbers_set.add(i)
return abundant_numbers_set
def is_sum_of_abundant(n):
v = abundant(n)
for i in range(1, n + 1):
if list(v).count(i) and list(v).count(n - i):
return True, i, n-i
return False
if __name__ == '__main__':
example = 24
print(is_sum_of_abundant(example))
Найти максимальный куб, который можно составить, убрав минимальное количество чисел из числа
Дано число N. Задача найти такой куб, который составляется из числа N путем удаления цифр.
Вход: 4125 Результат: 125 Объяснение: 125 = 5^3. Можно составить 125, убрав 4 из числа 4125 Вход: 876 Результат: 8 Объяснение: 8 = 2^3. Можно сформировать 8, убрав 7 и 6 из числа 876
import math
def perfect_cubes(limit):
cubes = list()
for i in range(1, math.ceil(limit ** (1. / 3.))):
cube = i ** 3
cubes.append(str(cube))
return cubes
def find_largest_cube(num):
cubes = perfect_cubes(num)
num = str(num)
cubes = cubes[::-1]
cubes_number = len(cubes)
# Цикл по всем кубам
for i in range(cubes_number):
current = cubes[i]
digits_count_in_cube = len(current)
index = 0
digits_count_in_number = len(str(num))
for j in range(digits_count_in_number):
# проверяем, что цифра в кубе совпадает с цифрой в числе
if num[j] == current[index]:
index += 1
if digits_count_in_cube == index:
return current
# Если цикл завершается, такого числа нет
return "Not Possible"
if __name__ == '__main__':
example = 4125
print(find_largest_cube(example))
Комментарии