Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.

В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.

Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.

Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.

Создание случайных чисел из семени

Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.

Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.

Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.

R(Input) -> Output

Начнём с того, что R - это простая функция, которая всего лишь прибавляет единицу.

R(x) = x + 1

Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, ... Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.

R(x) = x + c

Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, ... Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало - круг из чисел!

Числовой круг

Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.

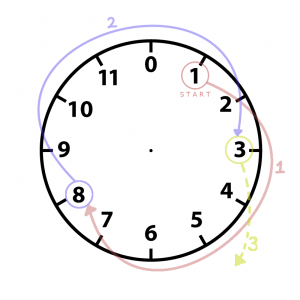
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.

Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.

Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.

R(x) = (x + c) % m

На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, ... что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.

Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.

До сих пор мы делали "прыжки" за счёт добавления, но что если использовать умножение? Умножим х на константу a.

R(x) = (ax + c) % m

Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:

1. (а - 1) должно делиться на все простые множители m
2. (а - 1) должно делиться на 4, если m делится на 4

Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.

Выбор семени

Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.

Еще один способ - это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.

Конечный результат

Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:

x(n) = (a * x(n - 1) + c) % m

Где начальное значение х - это семя, а - множитель, с - константа, m - оператор остатка от деления.

То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.

В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.

Заключительные замечания

Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.

Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.

На этом всё, спасибо что прочитали!

Оригинал статьи