В предисловии любого учебника по матанализу написано, что математический анализ:
- Является одним из основных направлений математики.
- Изучает функции и их свойства, и то, как они изменяются на протяжении времени.
- Состоит из двух основных разделов – дифференциального и интегрального исчисления.
Этих пояснений явно недостаточно для того, чтобы заинтересовать студентов, и потому авторы иногда еще добавляют, что матанализ широко применяется в научных, финансовых и инженерных вычислениях:
- Дифференциальное исчисление изучает производные функций, которые описывают, как быстро меняется значение функции в зависимости от ее входных параметров. Применяется для решения задач, связанных с оптимизацией, моделированием физических процессов, анализом данных, и так далее.
- Интегральное исчисление изучает интегралы функций, которые описывают, какие значения функции накапливаются на протяжении времени. Используется для решения задач, связанных с подсчетом площадей, объемов, масс, анализом вероятностей.
Если матанализ изучается в отрыве от практики (не на инженерном факультете), связь между абстрактными вычислениями и решением прикладных задач, скорее всего, останется неясной: в явлениях и событиях окружающего мира сложно узнать функции из учебника, и наоборот – функции в учебнике не напоминают явно какие-то определенные объекты и процессы из реальной жизни. В результате складывается впечатление, что матанализ – не только сложная, но еще и максимально абстрактная тема.
Однако матанализ действительно применяется для решения самых приземленных, повседневных, практических задач, и в нем гораздо проще разобраться, если понять, как именно используется в реальной жизни, в нашем случае – в разработке ПО.
Математический анализ в программировании
На самом базовом уровне, общем для всех направлений программирования, матанализ используется для оценки, оптимизации и адаптивной настройки алгоритмов. С помощью анализа сложности можно:
- Оценить время выполнения алгоритма. Так, алгоритм сортировки сложности O(n log n) будет более эффективным, чем алгоритм сложностью O(n^2), когда размер данных увеличивается в разы.
- Определить способы оптимизации алгоритма – к примеру, анализ может показать, что данные должны быть отсортированы перед обработкой, или что оптимальная скорость работы программы достигается при использовании определенной структуры данных – скажем, хэш-таблицы вместо списка.
- Создать адаптивный алгоритм, который, возможно, будет изменять количество потоков выполнения в зависимости от количества доступных ядер процессора или автоматически выбирать наилучшую структуру для работы с определенным набором данных.
Помимо этих и многих других общих задач, матанализ позволяет решать конкретные, специфические проблемы в различных сферах разработки.
Машинное обучение и искусственный интеллект
Здесь с помощью матанализа создают и оптимизируют модели, оценивают градиенты и решают дифференциальные уравнения:
- Оптимизация. Модели машинного обучения часто оптимизируют с помощью градиентного спуска. Цель такой оптимизации – найти набор параметров модели, которые минимизируют определенную функцию потерь.
- Оценка градиентов. В алгоритме обратного распространения, который используется для обучения нейронных сетей, градиенты функции потерь относительно весов и смещений сети вычисляются с помощью цепного правила.
- Решение дифференциальных уравнений. Многие задачи в машинном обучении и ИИ связаны с решением дифференциальных уравнений, которые описывают скорость изменения системы во времени. Решение этих уравнений позволяет моделировать широкий спектр физических и биологических систем – от распространения болезней до поведения финансовых рынков.
Data science и анализ данных
В этой сфере тоже не обойтись без математического анализа – он используется в разработке алгоритмов регрессии, классификации и кластеризации данных. Вот всего несколько примеров того, как разные аспекты матанализа позволяют решать прикладные задачи:
- Производные – помогают понять, как функция изменяется в зависимости от входных данных.
- Интегралы – позволяют вычислить все накопленные изменения функции.
- Многомерное исчисление – применяется для анализа функций многих переменных, что важно для понимания сложных наборов данных.
- Оптимизация – позволяет найти минимум или максимум функции, или, другими словами – наилучшее решение проблемы.
- Дифференциальные уравнения – как уже упоминалось выше, помогают моделировать и прогнозировать сложные события и процессы.
Финансовое ПО
Вот несколько примеров, как математический анализ используется в финансовом ПО:
- Моделирование финансовых процессов. С помощью матанализа можно создавать модели, которые описывают любые финансовые процессы – изменения котировок, ставок по кредитам, валютных курсов и так далее. Такие модели используют для прогнозирования динамики цен, оценки рисков и определения оптимальных стратегий инвестирования.
- Анализ рисков. Матанализ и матстатистика позволяют предсказывать вероятность возникновения различных финансово-экономических событий – изменений котировок акций и курсов валют, обвалы фондового рынка и т.п.
- Определение оптимальных стратегий инвестирования. Матанализ поможет максимизировать прибыль и одновременно минимизировать риски путем распределения портфеля между различными активами.
- Анализ эффективности. Математический анализ позволяет оценить эффективность различных инвестиционных стратегий и портфелей. Для этого используется анализ доходности, волатильности и других параметров, которые позволяют установить, какие стратегии и портфели являются наиболее эффективными.
Научный, медицинский и инженерный софт
Математический анализ здесь используется в нескольких целях:
- Моделирование и симуляция. С помощью матанализа создают математические модели различных объектов, процессов и систем. Эти модели затем используются для симуляции и анализа поведения объектов и процессов. Например, в инженерном ПО моделирование может использоваться для определения прочности конструкций или для моделирования процессов теплопередачи. В научном ПО моделирование используют для изучения физических закономерностей и процессов в природе.
- Численные методы. Матанализ применяют для разработки и реализации численных методов, которые используются для решения математических задач на компьютере. Например, численные методы могут использоваться для решения дифференциальных уравнений и оптимизации функций.
- Обработка сигналов. При помощи матанализа анализируют и обрабатывают сигналы из самых разных источников – от показаний датчиков и звука до изображений и видео. Это позволяет создавать ПО для распознавания образов, анализа речи или обработки сигналов с медицинских приборов.
- Оптимизация. Математический анализ используется для нахождения наилучших решений различных задач – от оптимизации производственных процессов до оптимизации параметров моделей.
Разработка игр
Как уже упоминалось выше, матанализ позволяет моделировать и симулировать сложные явления, процессы и поведение объектов. По этим причинам матанализ необходим в геймдеве – здесь он:
- Обеспечивает реалистичное поведение объектов в игровом мире. Например, помогает определить скорость и ускорение объектов в зависимости от сил, действующих на них, позволяет вычислить момент столкновения объектов, моделирует поведение веществ в зависимости от их плотности.
- Повышает реалистичность графики – позволяет определить перспективу и проекцию объектов на экране, используется для расчета теней, направления освещения и определения геометрических форм объектов.
- Оптимизирует производительность – ускоряет работу алгоритмов рендеринга, уменьшает количество полигонов в моделях объектов.
В матанализе не разбираюсь, что делать?
Есть три способа решить эту проблему:
- Изучить и прорешать пару хороших книг по матанализу.
- Воспользоваться подходящей математической библиотекой.
- Пройти интенсивный курс, где быстро и доступно дадут всю необходимую базу для конкретной сферы разработки.
Лучшие учебники по матанализу
К сожалению, на русском языке практически не издают книги, посвященные применению матанализа в конкретных сферах разработки. Но хорошие и понятные книги, которые подходят для самостоятельного изучения матанализа в целом – конечно же, есть. В первую очередь это «Математический анализ» В.А. Зорича. Главные плюсы этого двухтомника – доступный язык и последовательная, хорошо продуманная подача материала. Автор умело объясняет сложные концепции и выстраивает структуру изложения материала так, чтобы читатель погружался в матанализ плавно, не испытывая необходимости прояснить ту или иную тему с помощью дополнительных пособий. Результат – фундаментальная база знаний обо всех аспектах матанализа.
Следующие три автора – Б. П. Демидович, Г. М. Фихтенгольц и Л. Д. Кудрявцев – признанные классики жанра. Под редакцией Б. П. Демидовича изданы самые исчерпывающие сборники задач:
- «Сборник задач и упражнений по математическому анализу»
- «Задачи и упражнения по математическому анализу для втузов»
Двухтомник Г. М. Фихтенгольца «Основы математического анализа» уделяет особое внимание прикладному использованию матанализа в физике, механике и технике.
Монументальный трехтомник Л. Д. Кудрявцева «Курс математического анализа» подробно рассматривает все аспекты классического и современного матанализа:
- Дифференциальное и интегральное исчисление функций одной переменной.
- Теория рядов, дифференциальное и интегральное исчисления функций многих переменных, теория дифференцируемых отображений, элементы дифференциальной геометрии.
- Элементы гармонического анализа.
Математические библиотеки
Во многих случаях для использования методов матанализа в приложении достаточно самого базового понимания концепций – большую часть работы возьмет на себя математическая библиотека. В экосистеме Python есть несколько замечательных библиотек:
- SciPy – используется для инженерных и научных расчетов.
- NumPy – бесплатная альтернатива MATLAB.
- SymPy – применяется для символьных вычислений.
- PyDSTool – мощный инструмент для моделирования и анализа динамических систем.
- SymEngine – супербыстрая C++ библиотека, которая легко интегрируется с Python и используется для символьных вычислений.
Продемонстрируем возможности библиотек NumPy и SciPy на примере системы Лотки-Вольтерры, которая моделирует динамику популяций хищников и жертв. Начальные условия x(0) = 10 и y(0) = 5 задают количество жертв и хищников соответственно. Параметры a, b, c и d определяют взаимодействие популяций:
- a – коэффициент естественного прироста жертв;
- b – коэффициент смертности жертв от хищников;
- c – коэффициент смертности хищников;
- d – отношение рождаемости хищников к числу съеденных жертв;
- t_max – максимальное время моделирования.
Первое решение задачи использует библиотеки NumPy и SciPy. Функция lotka_volterra задает систему дифференциальных уравнений. Затем задаются начальные условия, параметры и временной интервал для решения системы. Функция odeint решает систему дифференциальных уравнений и возвращает значения популяций жертв и хищников на каждом шаге времени:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# уравнения системы Лотки-Вольтерры
def lotka_volterra(xy, t, a, b, c, d):
x, y = xy
dx_dt = a * x - b * x * y
dy_dt = -c * y + d * x * y
return [dx_dt, dy_dt]
# начальные размеры популяций
init = [10, 5]
# параметры системы
a, b, c, d = 1, 0.1, 1.5, 0.075
# временные границы
t_max = 50
t = np.linspace(0, t_max, 1000)
# решаем систему уравнений
sol = odeint(lotka_volterra, init, t, args=(a, b, c, d))
# выводим график
plt.plot(t, sol[:, 0], label='Жертвы')
plt.plot(t, sol[:, 1], label='Хищники')
plt.legend()
plt.xlabel('Время')
plt.ylabel('Популяция')
plt.show()
Результаты моделирования отображаются на графике, который показывает изменение популяции жертв и хищников в зависимости от времени:
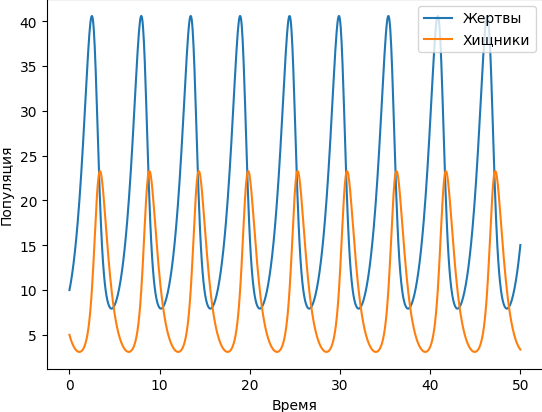
Во втором решении математические библиотеки не используются, и система уравнений решается методом Эйлера:
import matplotlib.pyplot as plt
# функция для решения системы Лотки-Вольтерры методом Эйлера
def solve_lv(init, a, b, c, d, dt, t_max):
# инициализация переменных
t_list = [0]
x_list = [init[0]]
y_list = [init[1]]
# цикл для вычисления решения
while t_list[-1] < t_max:
x_n = x_list[-1] + dt * (a * x_list[-1] - b * x_list[-1] * y_list[-1])
y_n = y_list[-1] + dt * (-c * y_list[-1] + d * x_list[-1] * y_list[-1])
t_n = t_list[-1] + dt
x_list.append(x_n)
y_list.append(y_n)
t_list.append(t_n)
return t_list, x_list, y_list
# начальные размеры популяций
init = [10, 5]
# параметры системы
a, b, c, d = 1, 0.1, 1.5, 0.075
# временные границы
t_max = 50
dt = 0.001
# решаем систему уравнений
t, x, y = solve_lv(init, a, b, c, d, dt, t_max)
# выводим график
plt.plot(t, x, label='Жертвы')
plt.plot(t, y, label='Хищники')
plt.legend()
plt.xlabel('Время')
plt.ylabel('Популяция')
plt.show()
Результат получается практически таким же:
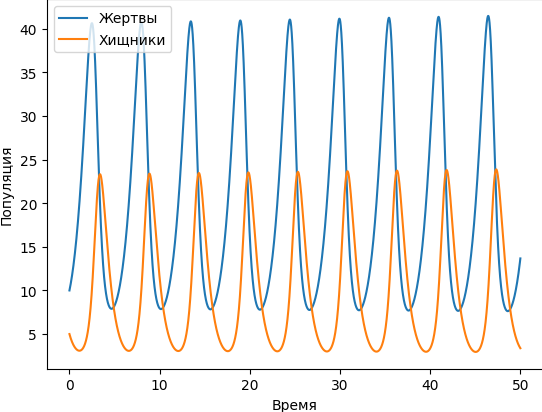
Курсы
Последняя (и самая эффективная!) опция – хороший курс, нацеленный на использование математического анализа в конкретной сфере разработки. Матанализ вполне реально освоить самостоятельно, но для этого нужны время, усилия и серьезная мотивация. Если нужно быстро подготовиться к прохождению ИТ-курса, который требует солидной базы по матанализу, проще записаться на интенсивную программу, где уже учтена специфика отрасли, а материал подается в эффективном, компактном и доступном формате – как курсе Библиотеки программиста «Математика для Data Science».


Что вам непонятно в матанализе? :)