Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.
Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.
Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.
Здесь и пригодится знание преобразования Фурье.
Что такое звук в математическом смысле?
Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.
Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.
Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.
Запишем определение:
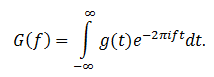
Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.
Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?
Геометрическая интерпретация преобразования Фурье
Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.
В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.
1. Наматываем сигнал
Давайте начнём с самого простого случая. Рассмотрим гармонический сигнал, совершающий 3 колебания в секунду (f0 = 3с-1):
g(t) = 1 + cos (6πt).
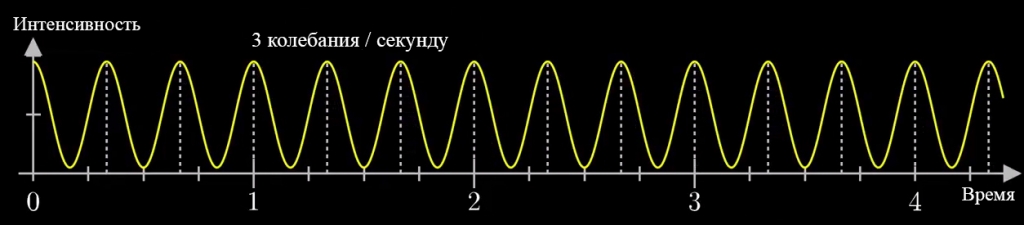
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.
Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения fВ = 0.5 об/с.
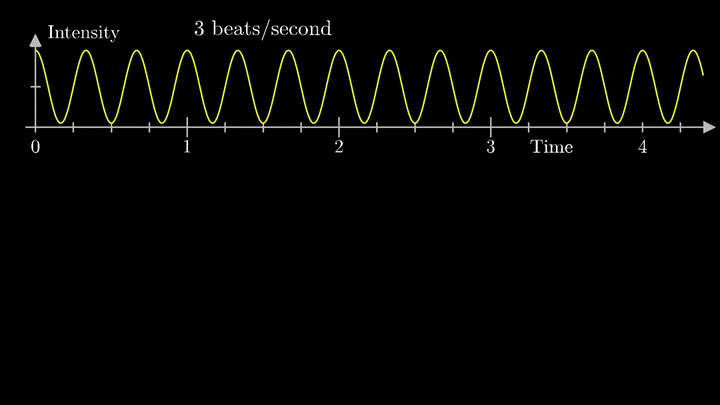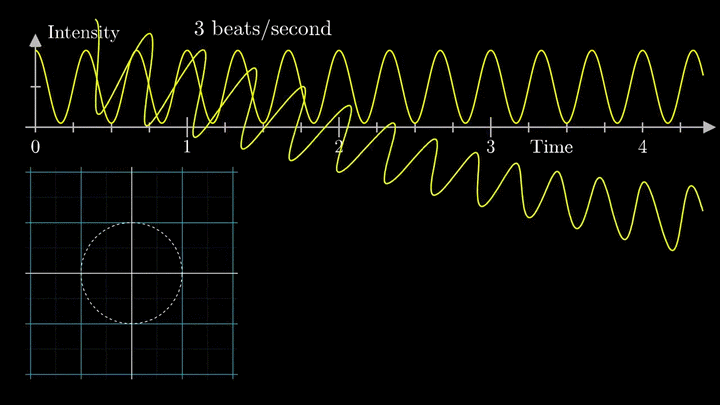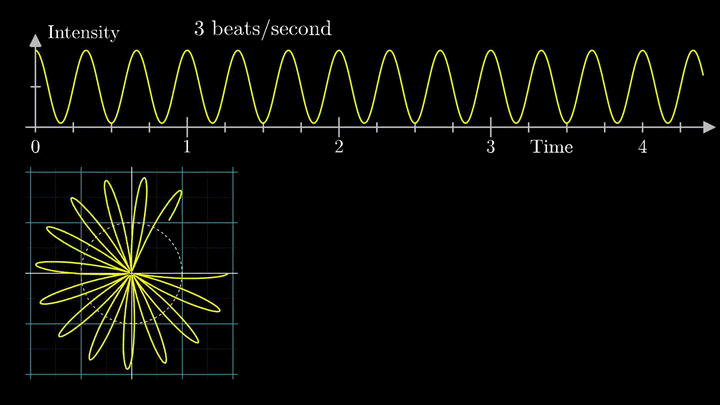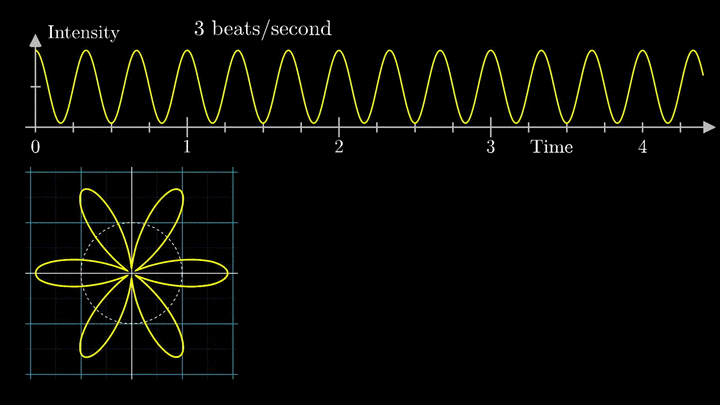
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная "намотка" сливается с началом координат, а при приближении к максимумам – отклоняется.
Пока выглядит не особо информативно, не так ли?
А теперь увеличим частоты намотки.
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения fВ = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.
2. Ищем центр масс
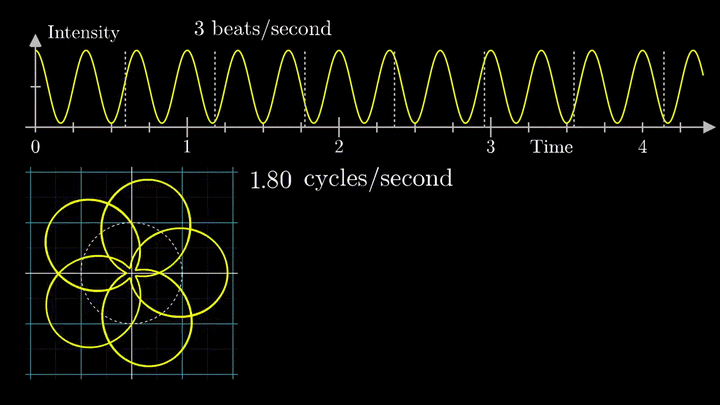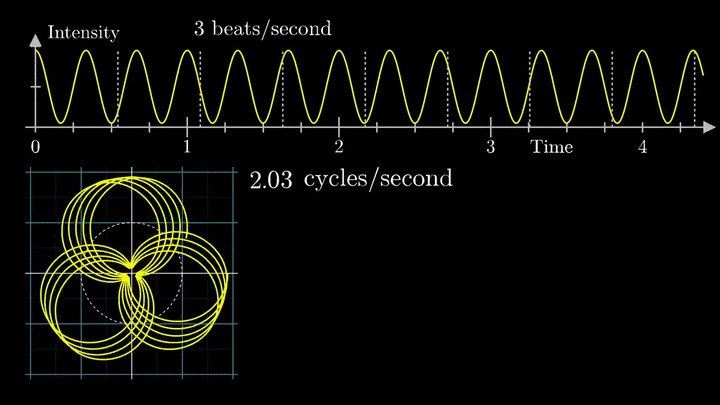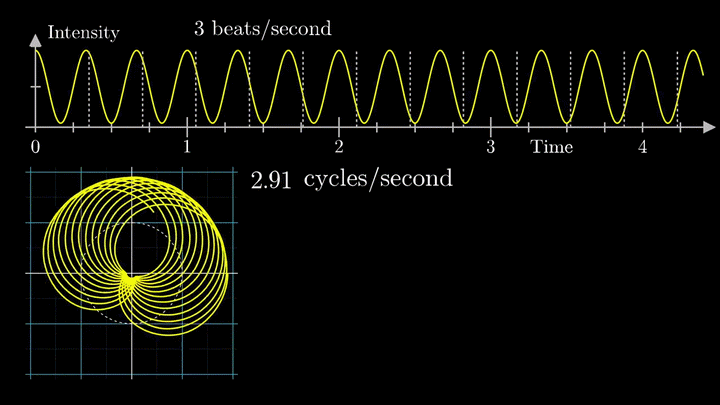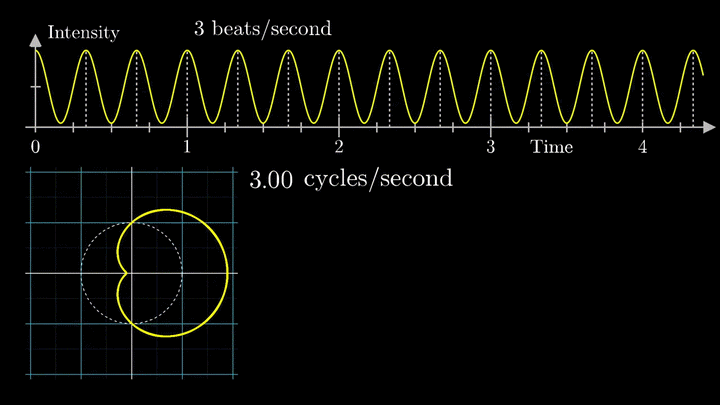
Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).
Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.
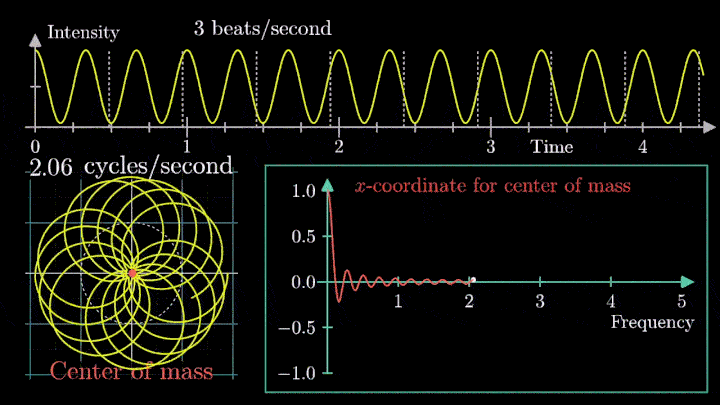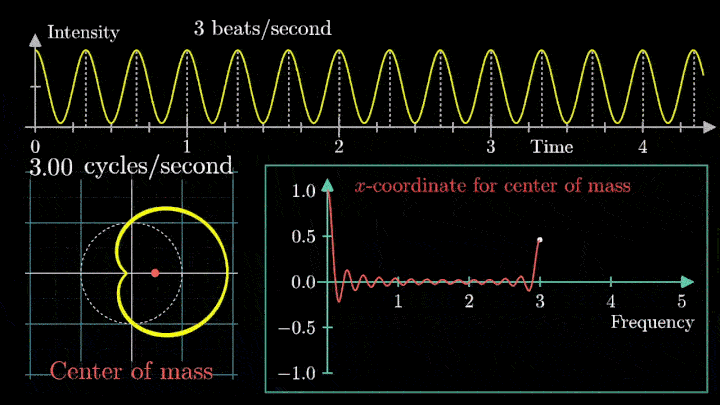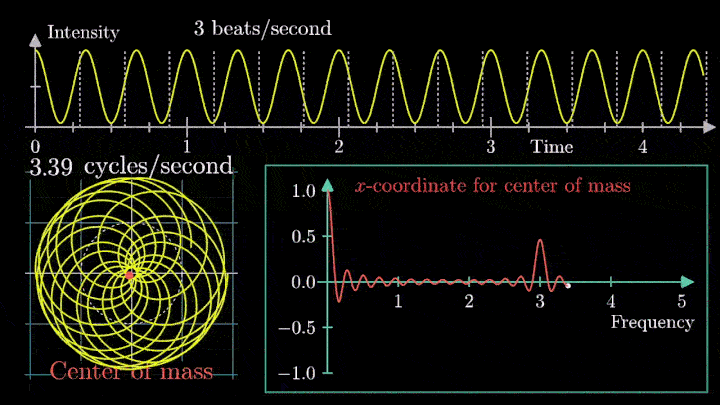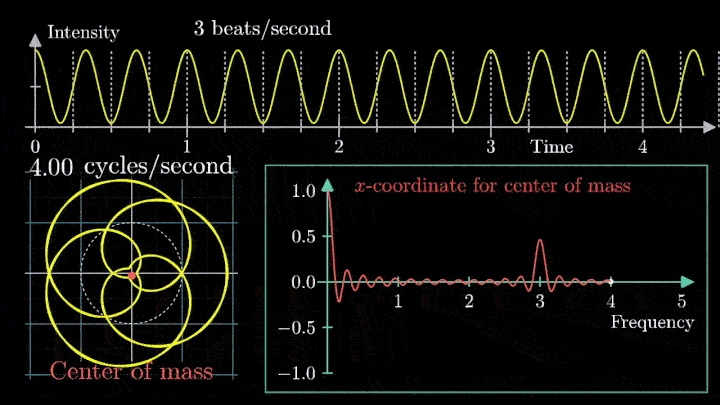
Мы видим два пика: в точках fВ = 0 об/с и fВ = 3 об/с. На основании такого поведения центра масс уже можно судить о частоте исходного сигнала (он колеблется с f = 3с-1).
Тогда что означает всплеск на низких частотах?
3. Анализируем влияние смещения
Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.
При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.
Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.
Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.
Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.
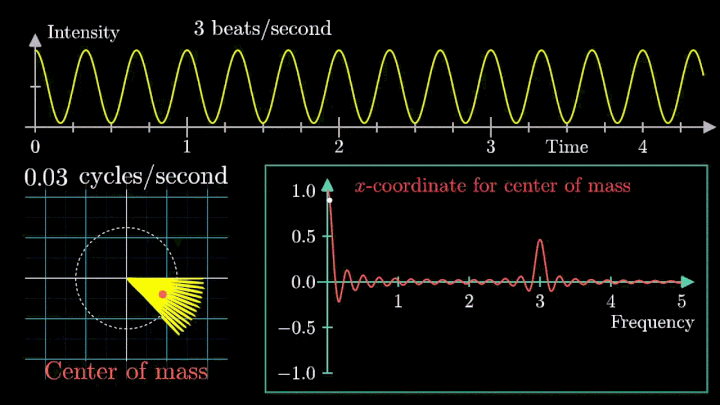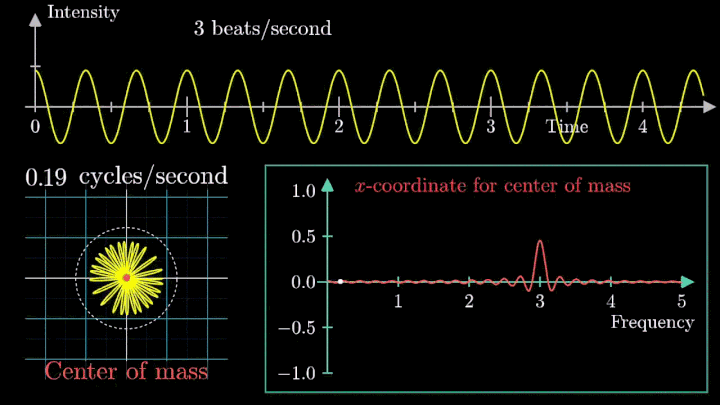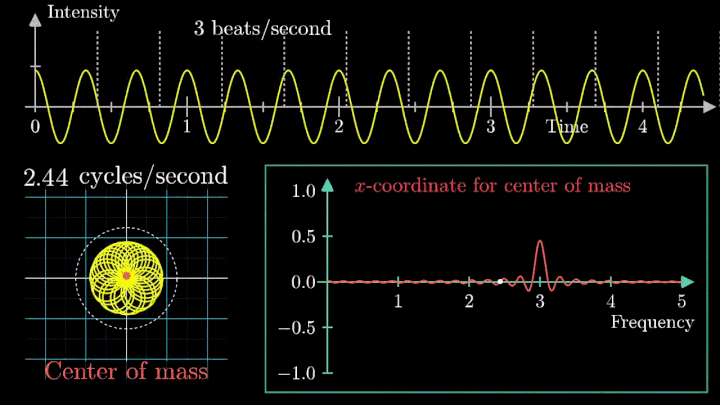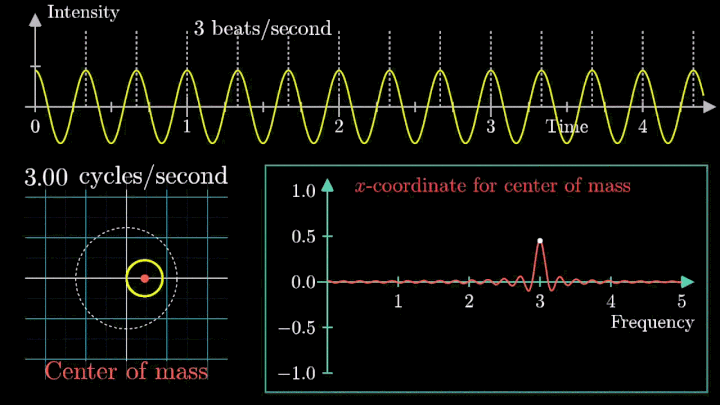
Таким образом, на графике остался только один резкий скачок.
Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.
4. Выделяем частоты полигармонического сигнала
Теперь рассмотрим сумму двух гармонических сигналов с частотой колебаний f1 = 2 с-1 и f2 = 3 с-1. Проделаем с ней те же операции – «намотаем» возле начала координат, и, меняя частоту вращения, построим график х-координаты центра масс.
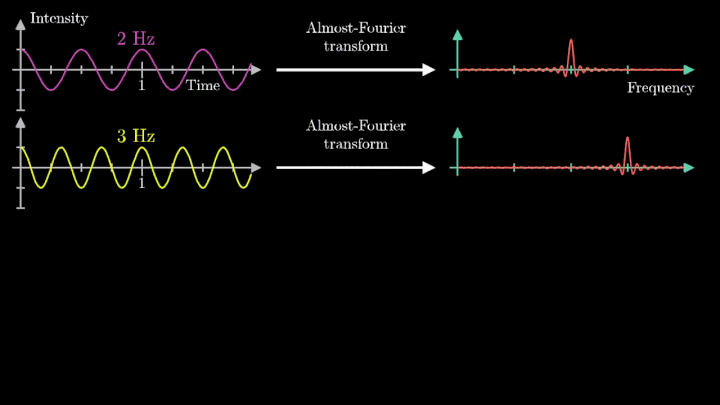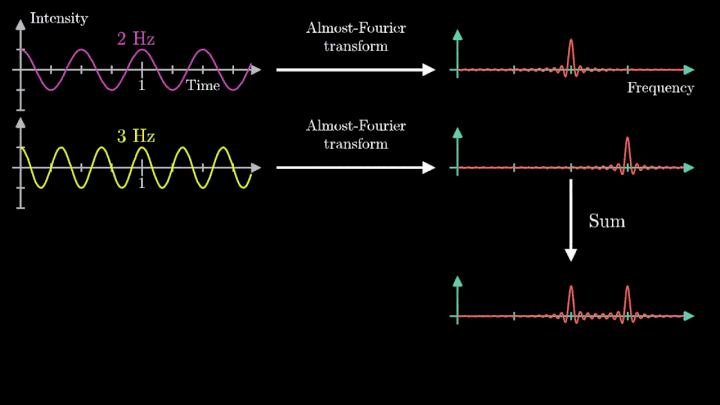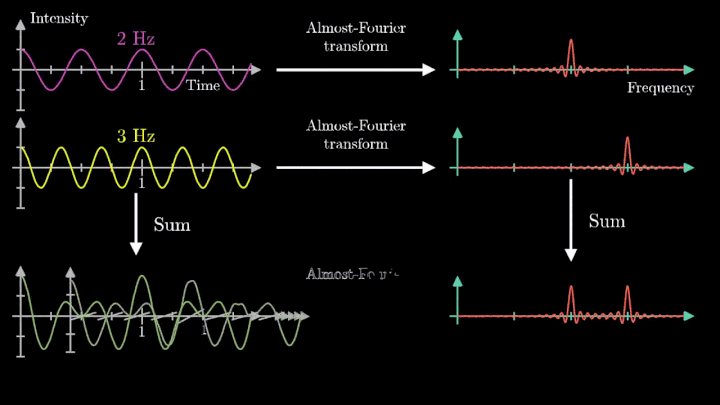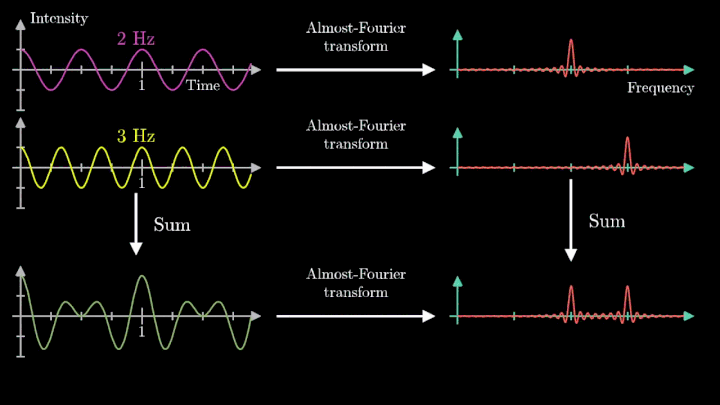
Мы наблюдаем два пика в точках fВ = 2 об/с и fВ = 3 об/с, что соответствует частотному составу исходной суммы.
Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.
Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.
Вывод преобразования Фурье
В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:
eiφ=cos(φ)+i·sin(φ).
Геометрически это соотношение означает, что при любом φ точка eiφ на комплексной плоскости лежит на единичной окружности.
Построим радиус-вектор eiφ при разных значениях φ.
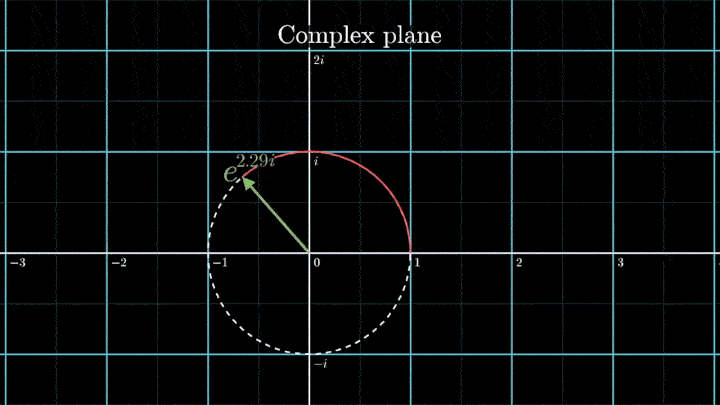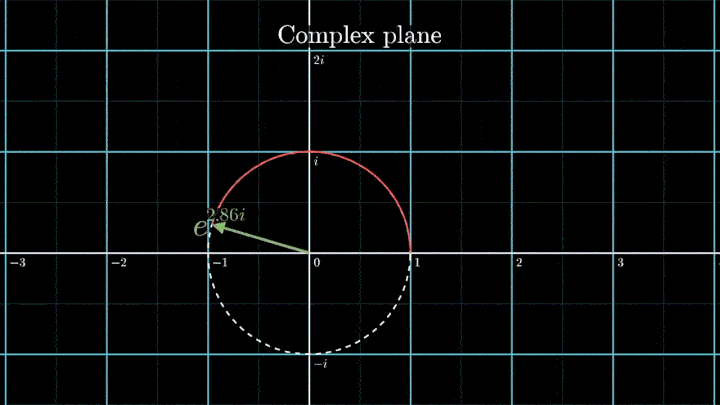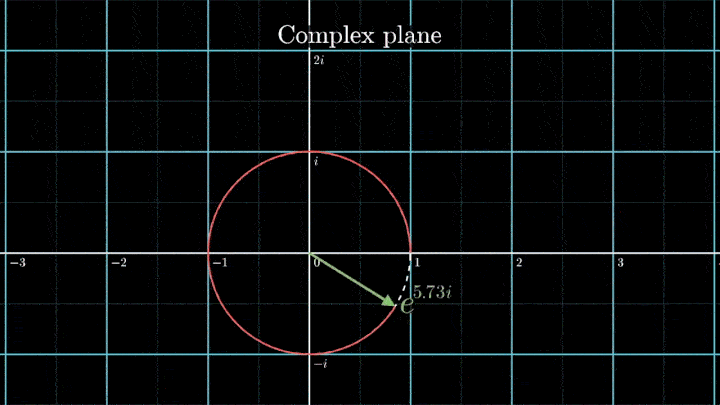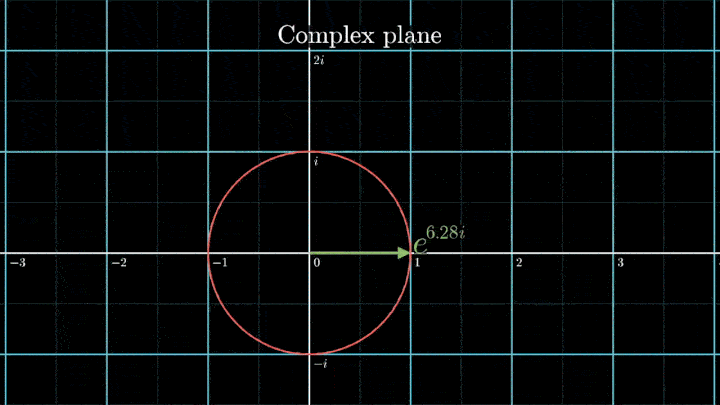
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.
Тогда намотка сигнала g(t) описывается как g(t)e-2πift.
Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:
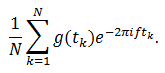
Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:
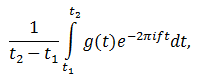
где t1 и t2 – границы интервала, на котором рассматривается сигнал.
Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.
Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.
Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.
Применение преобразования Фурье для фильтрации
Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.
При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.
После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.



Комментарии