📱🧮 Думаешь, каждый может сделать крутой калькулятор? Как Android обошел iOS в создании идеального калькулятора

На первый взгляд, нет ничего проще, чем разработка программного калькулятора: это один из стандартных мини-проектов для всех начинающих программистов. Но, оказывается, даже профессиональные разработчики не всегда пишут калькуляторы правильно. У iOS-калькулятора есть проблемы с точностью – он некорректно вычисляет значение выражений. К примеру, результат (10^100) + 1 − (10^100) должен быть равен 1, но калькулятор считает, что 0:

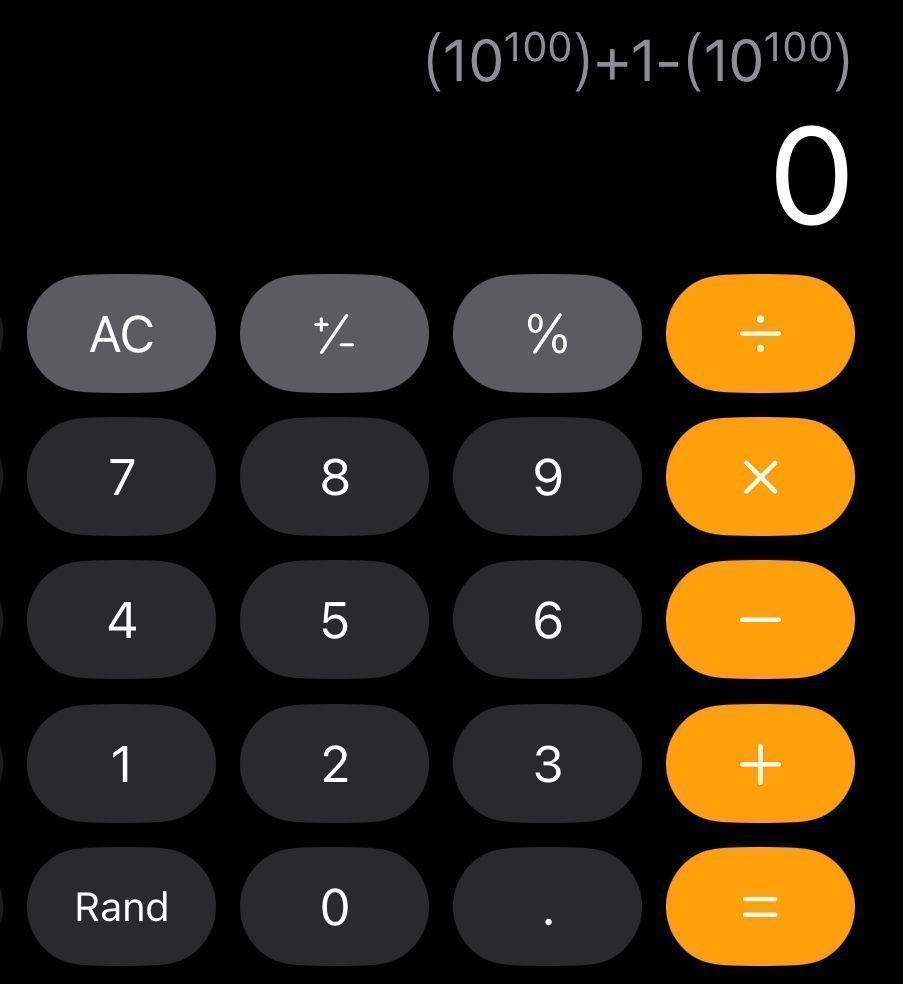
А калькулятор Android, напротив, выдает правильный результат:

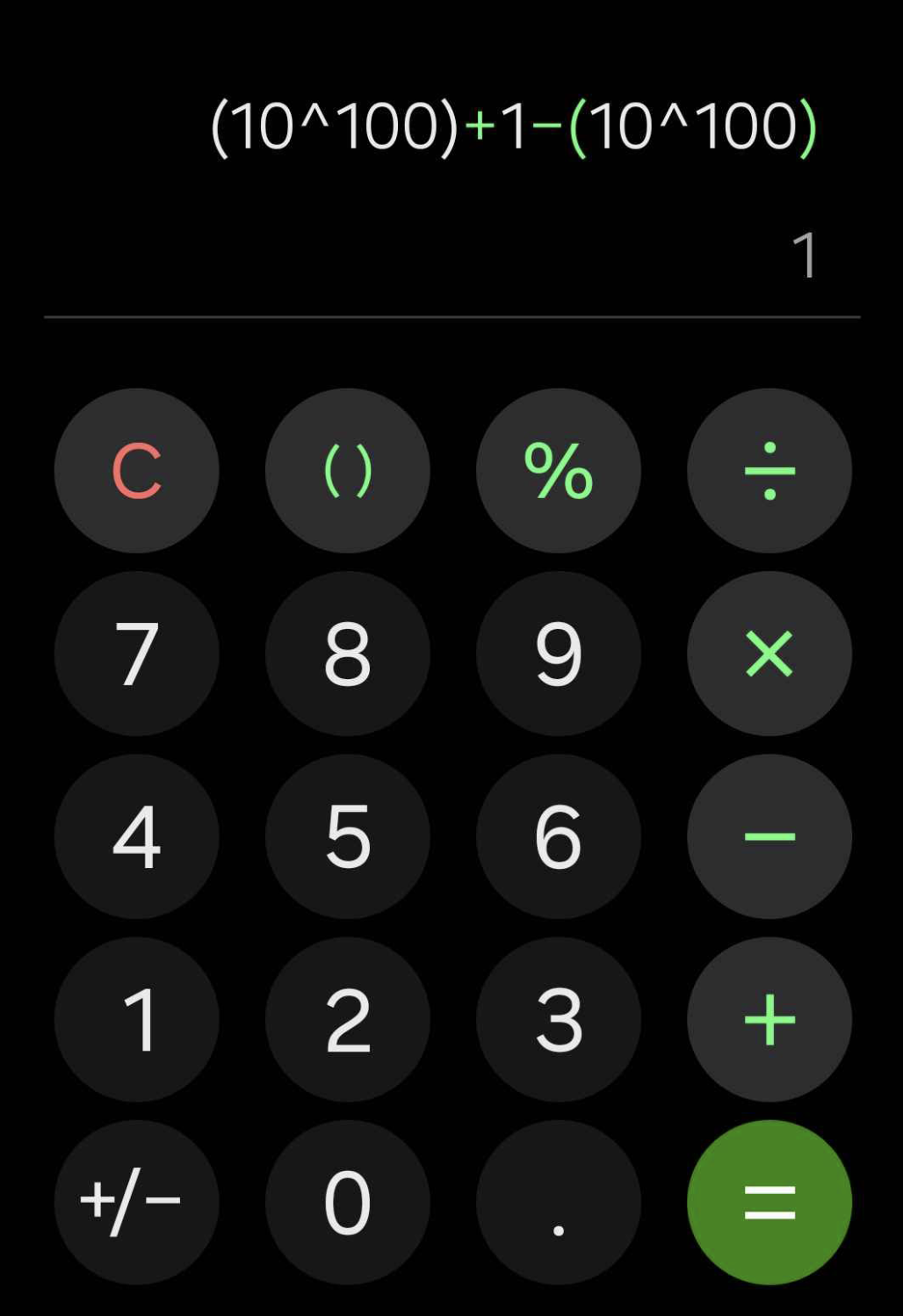
История того, как разработчикам Android удалось сделать правильный калькулятор – настоящий триллер: реализацию этого проекта пришлось поручить одному из ведущих C/C++ инженеров.

Почему так сложно сделать точный калькулятор

Ханс-Юрген Бём известен разработкой сборщика мусора для C/C++. В 2014 году компания Google наняла Бёма из-за его выдающейся экспертизы в области управления памятью и параллельного программирования – он возглавил важнейшую работу по определению семантики разделяемых переменных в C++. А потом ему дали по-настоящему сложную задачу – разработку правильного калькулятора. В процессе Бём и его команда столкнулись со множеством неожиданных проблем.

Проблема 1: числа с плавающей запятой

Если вы складываете 0,1 и 0,2, то ожидаете получить 0,3, верно?

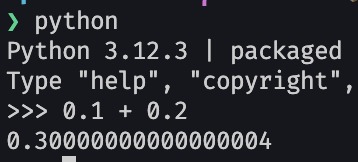
Дело в том, что компьютер работает с числами с плавающей запятой. Этот формат похож на то, как мы записываем очень большие или очень маленькие числа в научной нотации, но с одним важным отличием: компьютер может использовать только определенное количество двоичных цифр для хранения числа. Это создает неожиданную проблему: некоторые числа, которые нам кажутся простыми, компьютер не может представить точно. Например:

• Число 0,3 в двоичной системе превращается в бесконечную периодическую дробь.
• Большие числа, скажем, 10¹⁰⁰, просто не помещаются в отведенное пространство памяти.

Чтобы давать правильные ответы на математические выражения, калькулятор должен уметь представлять числа. Oднако почти все числа невозможно точно выразить в формате IEEE с плавающей запятой – даже простые операции требуют специального подхода для получения точного результата:

Проблема 2: большие числа

В большинстве языков программирования обычные числовые типы (например, int для целых чисел) имеют фиксированный размер в памяти:

• 2 байта – обычно для short (от -32 768 до 32 767)
• 4 байта – обычно для int (от -2 147 483 648 до 2 147 483 647)

Это значит, что они могут хранить числа только в определенном диапазоне, и соответственно, не обеспечивают нужную точность вычислений. Многие проблемы с точностью можно решить, используя большие числа – они не имеют ограничений по размеру и занимают столько памяти, сколько нужно, увеличиваясь по мере роста числа:

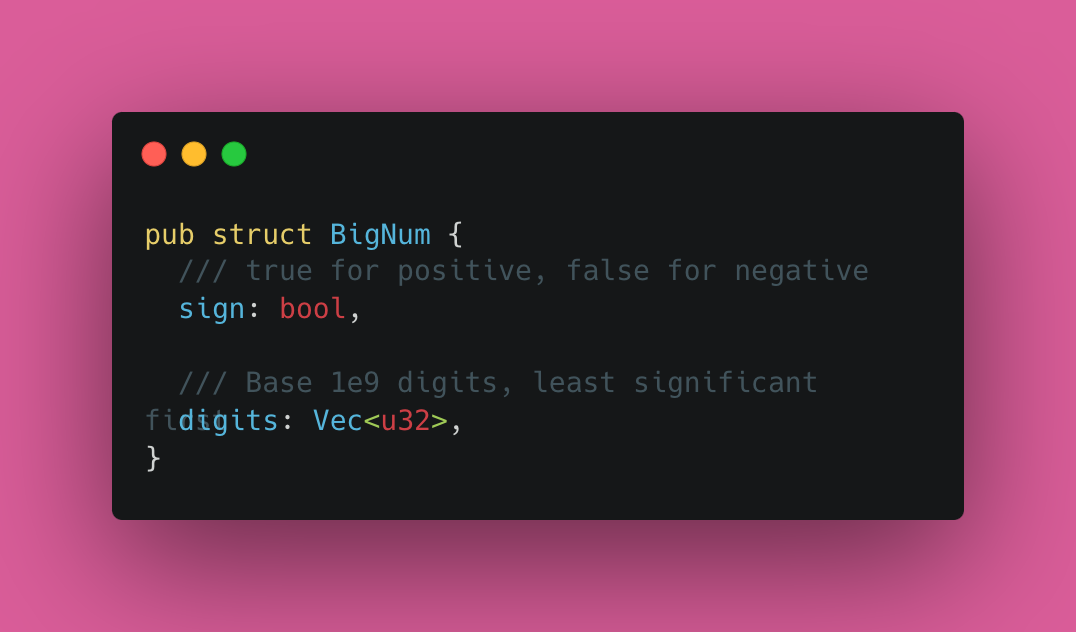
Для работы с дробями можно использовать большие числа и для числителя, так и для знаменателя. Операции сложения, вычитания, умножения и деления будут выполняться точно, потому что дробь можно всегда сократить или представить в виде числителя и знаменателя без округлений:

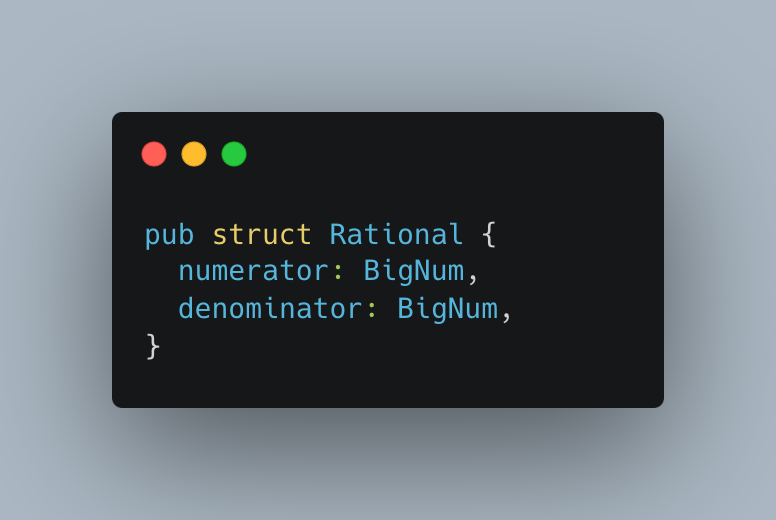
Но что делать с иррациональными числами? Тут возникает проблема. Даже если у нас есть дроби с бесконечной точностью, невозможно представить, например:

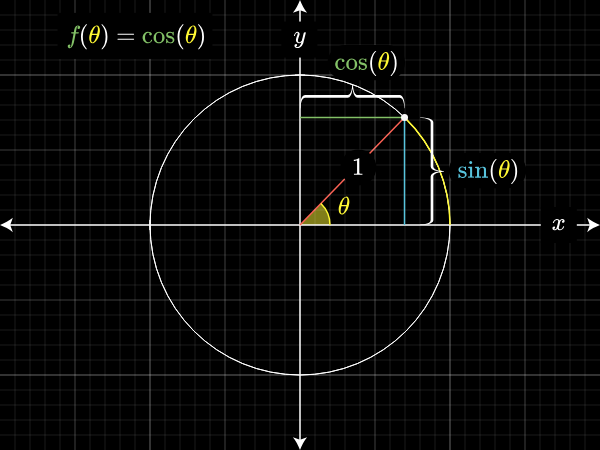
• π (отношение длины окружности к диаметру);
• √2 (длину диагонали квадрата со стороной 1).

Оба числа — иррациональны, у них нет точного дробного представления.

Проблема 3: алгебраическое представление чисел

Вместо того, чтобы хранить число как дробь, можно задать уравнение, решением которого будет нужное число. Например, x² − 2 = 0 для √2 (дополнительно указываем, что берем положительный корень). Арифметические операции с такими числами выглядят довольно сложно, например:

• Для сложения нужно создать новый многочлен, корень которого будет суммой исходных чисел.
• Для умножения применяется техника композиции многочленов или результант (математический инструмент для поиска многочлена общего корня).

Но есть подвох: этот подход работает только для алгебраических чисел, которые можно описать уравнением с целочисленными коэффициентами. Но что делать с π или е? Такие числа называются трансцендентными, их нельзя описать с помощью подобных уравнений.

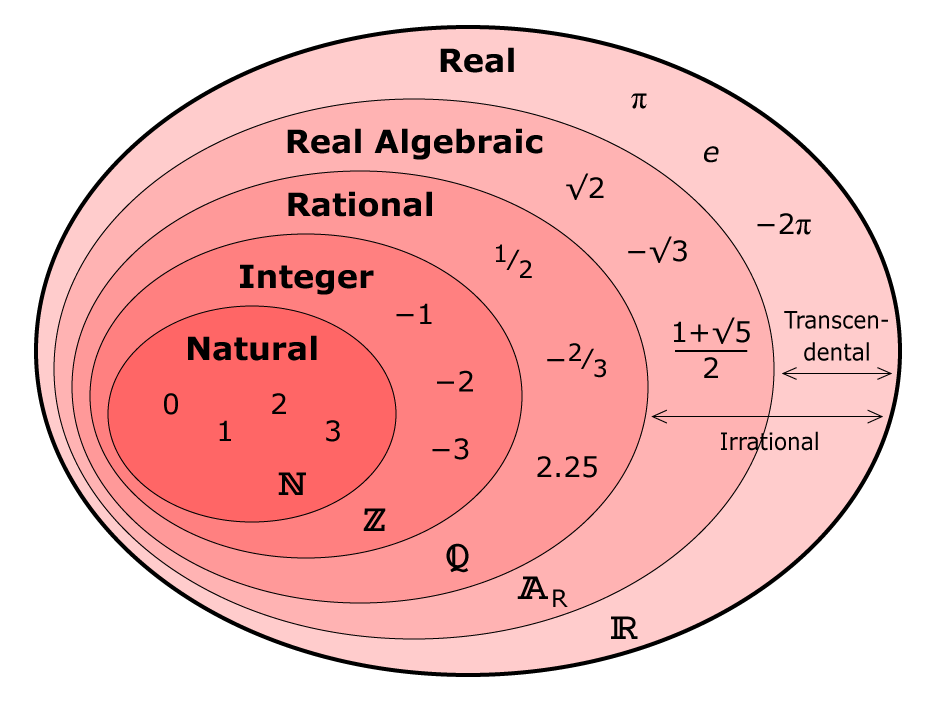
Возможное решение: конструктивные вещественные числа и рекурсивная арифметика

Итак, разработчики правильного калькулятора отбросили описанные выше тривиальные подходы, потому что:

• Целые числа поддерживают бесконечно большие числа, но только целые.
• Рациональные числа гарантируют точность дробей, но не покрывают иррациональные числа.
• Алгебраические числа, выраженные через уравнения, не могут точно представить π или е.

Следующим шагом стали конструктивные вещественные числа. Это числа, которые мы можем вычислять с любой заданной точностью. Давайте разберем на примере числа π:

• Мы не можем записать все десятичные знаки π, их бесконечно много.
• Но если нам нужно число, отличающееся от π не более чем на 0,01, можно использовать 3,14.
• 3,14 находится в пределах 0,01 от истинного значения π, поэтому это допустимый ответ.

Теперь рассмотрим более сложный пример – найти 2π с точностью 0,01:

• Нужно умножить π на 2.
• При умножении на 2 погрешность тоже умножается на 2.
• Значит, нам нужно найти π с точностью 0,005 (потому что 0,005 × 2 = 0,01).
• Берем 3,141 (оно отличается от π менее чем на 0,005).
• Умножаем 3,141 × 2 = 6,282.
• Получаем ответ, который гарантированно отличается от 2π не более чем на 0,01.

В рекурсивной вещественной арифметике каждое число – это функция, которая:

• Принимает на вход рациональное число (это желаемая точность).
• Возвращает рациональное число (это приближение).
• Гарантирует, что возвращаемое число отличается от истинного значения не больше, чем на заданную точность.

Проблема с рекурсивной вещественной арифметикой

Основное преимущество рекурсивной вещественной арифметики (RRA) – простота использования: вы просто указываете, какая точность нужна в конечном результате, а система сама рекурсивно определяет, с какой точностью нужно выполнять все промежуточные вычисления. Можно спокойно работать с иррациональными числами. Наверняка разработчики на этом остановились? А вот и нет. Дело в том, что приближенный характер вычислений RRA обеспечивает нужную точность, но портит пользовательский опыт: в качестве значения выражения 1 – 1 или sin(π) юзер увидит в калькуляторе не ожидаемый простой 0, а 0,0000000000000.

С другой стороны, e^(-1000) – очень маленькое число, но не 0. Если пользователь действительно получит такое число в качестве правильного результата, он должен иметь возможность прокрутить результат, чтобы увидеть ненулевые цифры.

Очевидно, что при создании калькулятора нужно как-то решать эту проблему и показывать точные значения там, где они есть, вместо приближенных. Однако решение этой проблемы связано со сравнением чисел, а эта задача в RRA принципиально нерешаема в случае с одинаковыми числами:

• Когда числа разные (если мы сравниваем, скажем 3,14 и 3,15), можно вычислять их с возрастающей точностью. В какой-то момент алгоритм увидит, что они точно разные, и сравнение завершится успешно.
• Но если числа одинаковые (когда мы сравниваем результат 1 – 1 и 0), алгоритм вычисляет разницу с точностью 0,1 → числа похожи; с точностью 0,01 → все еще похожи; с точностью 0,001 → опять похожи... И так будет продолжаться бесконечно: алгоритм никогда не сможет с уверенностью определить, что эти числа равны.

На этом этапе Бём и его коллеги пришли к важному выводу: чтобы решать практические задачи, вовсе не обязательно работать со всеми конструктивными вещественными числами. Достаточно ограничиться только теми числами, которые можно получить с помощью операций, доступных на калькуляторе:

• Арифметические операции – сложение, вычитание, умножение, деление и извлечение квадратного корня.
• Тригонометрические функции – синус (sin), косинус (cos), тангенс (tan) и их обратные функции (арксинус, арккосинус, арктангенс).
• Показательные и логарифмические функции – экспонента (exp) и натуральный логарифм (ln).

Полный набор конструктивных вещественных чисел бесконечно огромен. Но если ограничиться только теми числами, которые можно получить через указанные функции, множество станет намного меньше и управляемее. И, на самом деле, эта задача уже была решена в 1994 году:

Задача сводится к вопросу: «Равно ли нулю некоторое выражение, состоящее из элементарных констант?» Чтобы получить ответ, применяют представленный в работе алгоритм. Если он завершится, ответ будет абсолютно точен – а завершается он всегда, кроме одного очень редкого случая, связанного с так называемой гипотезой Шанюэля. Это одна из важнейших нерешенных гипотез в теории чисел. Она касается связи между экспоненциальными и логарифмическими числами. Никто пока не смог ни доказать ее, ни найти контрпример.

Однако решение, предложенное Ричардсоном и Фитчем, имеет один недостаток – оно очень медленное. К примеру, чтобы определить с помощью их алгоритма, что число 1 не равно 1 – e^(-e^1000), понадобилось бы больше шагов, чем атомов во Вселенной!

Гениальная идея: комбинация двух систем

Напомню, что изначально Бём и его коллеги хотели определить равенство конструктивных вещественных чисел, но это оказалось невыполнимо. После ограничения множества доступными на калькуляторе операциями задача стала решаемой, но это решение было чудовищно медленным. И тогда разработчики подумали: а обязательно ли всегда показывать идеально точное число? Если ответ – ровно 0, пусть будет 0,000000…, это не так уж страшно, пользователи переживут. Главное – не показывать 0 там, где на самом деле нужно 0.0000001. Таким образом, можно использовать консервативный алгоритм, который:

• Быстро скажет: «Это точно не ноль» или «Возможно, ноль, но нужно уточнить».
• Избежит ошибок там, где важна точность.

Для этого нужно было как-то скомбинировать оба подхода так, чтобы использовать их преимущества:

1. Рациональная арифметика:

• Всегда дает точные результаты.
• Но не может представить иррациональные числа (π, e и т. д.)

2. Рекурсивная вещественная арифметика:

• Может работать с любым конструктивным вещественным числом, включая π, √2 и т. д.
• Но не может дать идеально точный результат – только приближенный.

При совместном использовании все решается просто:

• Если пользователь делает обычные вычисления – хватит рациональной арифметики.
• Если же во вводе появляется что-то сложное (π, е, √2 и т. д.) – нужно подключить RRA.

Символьное представление известных чисел

Осталось решить проблему с представлением чисел. Сначала разработчики планировали представлять любое число как произведение рационального числа на RRA-число, но оказалось, что в этом случае точность пропадает:

И тогда они подумали: а нужно ли всегда использовать RRA, если число известно заранее?

Пример с π:

• RRA может дать приближение: «Хочешь π с точностью до 0,001? Получи 3,141».
• Но если мы уже знаем, что это π, почему бы не просто оставить его как символ «π», вместо бесконечного приближения?

Это называется символьным представлением – мы храним число как знак или формулу, а не бесконечное приближение:

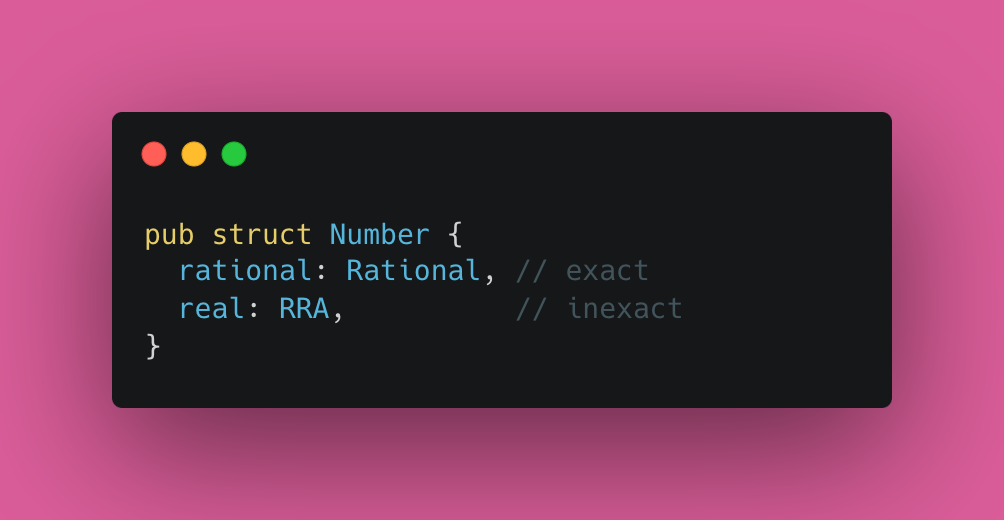
Эту идею разработчики решили использовать не только для π, но и для других известных чисел и функций (√arg, eᵃʳᵍ, ln(arg), log₁₀(arg), sin(πarg), tan(πarg) и т. д., где arg всегда является рациональным числом). Теперь любое число они записывали как Рациональное число × Вещественное число, причем вещественное число могло быть двух типов:

• Символьное число (π, е, √2).
• RRA-число (если точного представления нет, используем RRA).

Как это работает на примерах:

• (1 × π) + (3 × π). Здесь оба слагаемых – это π, представленные символьно. Значит, можно просто сложить рациональные коэффициенты: 1 + 3 = 4 и получить 4π.
• (1 × π) + (3 × √2). Здесь складывать разные символы π и √2 нельзя, придется использовать RRA для приближенного результата.

Итог

Разработчики Android-калькулятора придумали гениально простое и максимально эффективное решение. Это золотая середина между точностью, скоростью и простотой:

• Результаты всех расчетов – всегда точные.
• Показываются только нужные цифры, без лишних нулей.

Их метод достигает 99% качества результата, который дала бы сложнейшая компьютерная алгебраическая система, но при этом реализовать и поддерживать его – в 100 раз проще.

Математика в Data Science: от базовых концепций до реальных задач

Знаете ли вы, что даже создание точного калькулятора требует глубокого понимания математики? А ведь это только верхушка айсберга в мире Data Science.

Почему математика критически важна:

• Работа с числами с плавающей запятой требует понимания погрешностей вычислений
• Большие данные нуждаются в специальных подходах к обработке
• Алгебраические представления и конструктивные числа — основа точных вычислений
• Без математического фундамента невозможно создавать эффективные алгоритмы

Наш курс от преподавателей ВМК МГУ поможет:

• Разобраться в тонкостях математических вычислений
• Освоить работу с разными типами данных
• Понять основы оптимизации алгоритмов
• Подготовиться к решению реальных задач в Data Science