🔢💡🌍 Математика в реальной жизни: 17 революционных концепций, изменивших мир

История науки полна прорывных идей, и некоторые из них оказали поистине фундаментальное влияние на развитие цивилизации: одни заложили основы механики и физики, другие изменили представления о случайности, информации и хаосе. Давайте разберемся, какие математические идеи стали краеугольными камнями научного прогресса.

1. Теорема Пифагора

Считается, что первое строгое доказательство соотношения между сторонами прямоугольного треугольника a² + b² = c² было сделано школой античного философа Пифагора в VI веке до н. э. Однако многие исторические источники говорят о том, что в том или ином виде соотношение было известно задолго до этого доказательства. Например, вавилонские глиняные таблички, датируемые 1800 г. до н. э., уже содержат примеры «пифагоровых троек» – чисел, удовлетворяющих уравнению (3-4-5, 5-12-13 и т.д.)

Как теорема используется в реальной жизни:

• При строительстве пирамид египтяне использовали веревки с узлами, чтобы измерять прямые углы. Они знали, что если сделать отрезки длиной 3, 4 и 5 единиц и натянуть их, получится идеальный прямой угол. Это обеспечивало ровные основания для пирамид.
• Современная навигация, в том числе GPS, основана на точных измерениях расстояний между спутниками и объектами на Земле. Для расчета положения устройства используются треугольники.
• В играх теорему Пифагора используют для вычисления расстояния между двумя объектами.
• Компьютерные томографы и МРТ сканеры создают изображение внутренностей человека с разных углов. Чтобы преобразовать плоские снимки в трехмерные модели, используются сложные математические алгоритмы, в основе которых лежит наша знаменитая теорема.
• Когда астронавты «Аполлона-11» высаживались на Луну, расчеты траектории их посадочного модуля учитывали форму поверхности Луны и расстояние до Земли. Пифагорова теорема помогала в расчетах углов спуска и траектории посадки.

💡Интересный факт

Теорему Пифагора доказали множеством различных способов – от геометрических построений до сложных алгебраических выкладок. Один из самых элегантных методов придумал президент США Джеймс Гарфилд в 1876 году – его доказательство использует свойства трапеции.

2. Логарифмы

В 1614 году шотландский математик Джон Непер опубликовал краткое описание логарифмов и их свойств. Логарифмы совершили настоящую революцию в вычислениях – до их появления математикам и астрономам приходилось тратить часы на сложные умножения и деления огромных чисел. Логарифмы позволили им свести эти операции к простому сложению и вычитанию.

Как логарифмы используются в реальной жизни:

• В 1624 году Кеплер опубликовал свой собственный вариант логарифмических таблиц. В то время он работал над вычислениями, связанными с орбитами планет. Раньше это занимало месяцы, но благодаря логарифмам он смог быстро обработать данные датского астронома Тихо Браге. В результате Кеплер открыл законы движения планет, ставшие основой для гравитационной теории Ньютона.
• До появления логарифмов морякам приходилось вручную вычислять координаты своего местоположения по звездам. С логарифмами расчеты стали проще и быстрее, а точность навигации повысилась.
• Во время Второй мировой войны инженеры и артиллеристы применяли логарифмы для расчетов траекторий снарядов. К примеру, британцы с помощью логарифмических вычислений создали радиолокационные системы, которые помогли выиграть Битву за Британию.
• В наши дни логарифмы используются в алгоритмах сжатия изображений и звука (JPEG, MP3), в машинном обучении, в ранжировании страниц (Google PageRank), в генетике и анализе биологических процессов (экспоненциальный рост бактерий, вирусов и т.д.)

💡Интересный факт

Наряду с первыми компьютерами в 1960-х инженеры NASA пользовались логарифмическими линейками. Именно с их помощью рассчитали траекторию полета и посадки «Аполлона-11» на Луну.

3. Производная функции

Формула производной была выведена Исааком Ньютоном в 1666 году, а независимо от него – Готфридом Лейбницем в 1675 году. Это открытие стало основой математического анализа, без которого невозможно представить современную науку и технологии.

Где применяют производные:

• Ньютон открыл закон всемирного тяготения благодаря производным. Он понял, что движение Луны вокруг Земли – это постоянное изменение скорости и направления, что можно описать через производные. Сегодня та же математика помогает рассчитывать орбиты спутников и траектории космических кораблей.
• Инженеры используют производные, чтобы анализировать нагрузки и деформации конструкций. Например, при проектировании сверхвысотного небоскреба Бурдж-Халифа (828 м) учитывались изменения силы ветра, и благодаря производным архитекторы смогли создать устойчивый дизайн.
• Производные используются в медицине, – например, в кардиологии для анализа изменения частоты сердечных сокращений, а в эндокринологии для оценки темпов изменения уровня инсулина у диабетиков.
• Современные нейросети учатся за счет градиентного спуска – метода, основанного на производных.

💡Интересный факт

Во время Великой лондонской чумы и столь же Великого лондонского пожара (1665-1666) Ньютон уехал из Кембриджа в родное поместье. Там, в одиночестве, он придумал свою теорию производных и открыл закон всемирного тяготения. Позже он назвал этот период своей жизни Annus Mirabilis – «год чудес».

Математика для дата-сайентистов: разбираемся без лишней воды

Proglib Academy Преподаватели ВМК МГУ собрали все, что реально нужно знать по математике в Data Science — никакой лишней теории, только то, что спрашивают на собеседованиях и используют в работе.

Что внутри:

• Матан — разберемся, зачем он вообще нужен в машинном обучении
• Линейная алгебра — перестанете бояться матриц и научитесь ими пользоваться
• Комбинаторика — считаем сложные штуки просто
• Теорвер и статистика — без этого в данных как без рук
• Машинное обучение на практике — применяем все изученное

Почему стоит попробовать:

• Те же задачи, что дают на входе в ШАД Яндекса
• Научитесь не тупить перед большими датасетами
• Поймете, как работают алгоритмы, а не просто будете их вызывать
• Можно задавать вопросы людям, которые реально в теме

4. Закон всемирного тяготения

В 1687 году Исаак Ньютон опубликовал фундаментальную работу «Математические начала натуральной философии», в которой сформулировал закон всемирного тяготения и три закона движения, ставшие основой классической механики. Ученый объяснил, почему Луна вращается вокруг Земли, почему яблоко падает на землю и почему Солнце удерживает планеты на своих орбитах.

До Ньютона никто не мог связать земные и космические силы одним законом: к примеру, немецкий астроном Иоганн Кеплер вывел законы движения планет, но он не знал, почему они так движутся. Ньютон доказал, что орбиты планет объясняются гравитацией.

Хотя теория Ньютона работает в большинстве случаев, она не объясняла, например, аномалию орбиты Меркурия. В 1915 году Эйнштейн усовершенствовал понимание гравитации, создав Общую теорию относительности, в которой гравитация – это не просто сила, а искривление пространства-времени.

Несмотря на теорию Эйнштейна, закон Ньютона до сих пор используется для расчета большинства орбит – от спутников GPS до миссий на Марс. К примеру, в 1957 году СССР запустил первый спутник «Спутник-1», рассчитав его траекторию по формулам Ньютона, а инженеры NASA использовали формулы Ньютона, чтобы высадить астронавтов на Луну (миссия «Аполлон-11» в 1969 году).

💡Интересные факты:

• Благодаря этому закону в 1846 году француз Урбен Леверье предсказал существование Нептуна: eго вычисления показали, что орбита Урана отклоняется от нормы из-за неизвестной планеты.
• История о том, что Ньютон открыл закон, когда увидел падающее яблоко, долгое время считалась легендой. Казалось логичным, что он не получил озарения мгновенно, но задумался: если яблоко падает вниз, значит, Земля притягивает его. Но почему тогда Луна не падает на Землю? Очевидно же, что гравитация действует на любом расстоянии, только сила уменьшается с квадратом расстояния. Однако в 2010 году ученые из Королевского общества нашли записи друга Ньютона, Уильяма Стакли, в которых подтверждается история про яблоко!

5. Волновое уравнение

До XVIII века никто не понимал, почему звук, свет и даже волны на воде ведут себя так, как мы их наблюдаем. Волновое уравнение, выведенное Жаном д’Аламбером в 1746 году, стало первой универсальной математической моделью, объясняющей распространение волн – от звуковых и световых до радиоволн и колебаний струн.

Как волновое уравнение применяется в реальной жизни:

• Каждый музыкальный инструмент создает звуковые волны, которые можно описать с помощью уравнения д’Аламбера. Например, в скрипке, фортепиано или гитаре струны колеблются, создавая звуковые волны в воздухе.
• Джеймс Клерк Максвелл расширил волновое уравнение для электромагнитных волн, доказав, что свет – это тоже волна. В итоге это открытие привело к созданию радиосвязи и телевидения.
• Все современные технологии, работающие с сигналами и радиоволнами – от Wi-Fi до 5G – используют принципы волнового уравнения.
• Волновое уравнение используется для предсказания цунами и волн в океане. Например, после землетрясения ученые могут рассчитать, когда и где волна достигнет берега. В 2004 году волновое уравнение помогло ученым спрогнозировать распространение разрушительного цунами в Индийском океане.

💡Интересные факты:

• Ваш смартфон передает и принимает радиоволны, которые подчиняются уравнению д’Аламбера. Без этой формулы не было бы мобильной связи.
• На основе волнового уравнения ученые разработали цифровую обработку звука, что позволило создать MP3-формат и современные аудиофильтры.

6. Мнимая единица

Мнимая единица – обычно комплексное число, квадрат которого равен −1. Формула i2 = -1 была выведена Леонардом Эйлером в 1750 году и долгое время считалась бесполезной: квадрат любого реального числа положителен, а тут вдруг –1! Однако со временем оказалось, что без мнимых чисел невозможно объяснить электричество, квантовую механику и даже компьютерную графику.

Как мнимая единица применяется на практике:

• В XIX веке Николай Тесла и Чарльз Стейнмец доказали, что переменный ток удобно описывать с помощью комплексных чисел (которые включают мнимую единицу i).
• Передача сигналов (радио, Wi-Fi, мобильная связь) основана на гармонических колебаниях, которые удобно описывать комплексными числами.
• В фундаментальных уравнениях квантовой механики – например, в уравнении Шредингера – используется i, потому что квантовые волновые функции ведут себя как комплексные числа.
• Комплексные числа помогают преобразовывать сигналы и вращать объекты в 3D. Когда ты играешь в игры или смотришь анимационные фильмы, ты видишь результат работы i.

💡Интересные факты:

• Все составные части энергоснабжающих систем – от розеток до мощных электростанций – рассчитаны с использованием комплексных чисел. Без этого электрические сети были бы менее эффективными.
• Без i не было бы квантовых компьютеров, которые сегодня разрабатывают Google и IBM

7. Теорема Эйлера для многогранников

Формула V – E + F = 2, представленная Леонардом Эйлером в 1751 году, показывает удивительную связь между количеством вершин (V), ребер (E) и граней (F) любого выпуклого многогранника. Эйлерову формулу можно назвать универсальным законом геометрии: oна работает для кубов, пирамид, додекаэдров и многих других фигур. Применяют ее в самых разных областях, от архитектуры до космологии.

Как используется теорема Эйлера для многогранников:

• Когда архитекторы проектируют здания с необычными формами, они используют принципы многогранников. Например, купола, мосты и даже современные небоскребы можно анализировать с помощью этой формулы.
• Многие молекулы, например фуллерены (молекулы углерода, похожие на футбольный мяч), имеют форму многогранников. Эйлерова формула помогает химикам предсказывать, какие структуры будут стабильными.
• В современной физике используется топология – наука о формах пространства, где Эйлерова формула играет ключевую роль. Например, ученые исследуют форму Вселенной, применяя этот принцип к моделям пространства-времени.
• Все 3D-модели в фильмах и видеоиграх состоят из многогранников (обычно треугольников). Графические движки используют формулу Эйлера, чтобы строить сложные объекты и рассчитывать их физику. Если у 3D-модели нарушена формула Эйлера (например, есть ошибка в ребрах или вершинах), она будет неправильно рендериться.

💡Интересные факты:

• В 1985 году ученые открыли молекулу фуллерена C60, которая идеально соответствует уравнению Эйлера.
• Купол Пантеона в Риме и знаменитый «Эдем» в Великобритании построены на основе многогранных структур, которые подчиняются формуле Эйлера.
• В 2003 году данные спутника WMAP показали, что форма Вселенной может быть додекаэдрической (многогранной), а это значит, что она тоже подчиняется формуле Эйлера.

8. Нормальное распределение

Во многих процессах, где есть случайность, числа подчиняются нормальному распределению. Например, рост людей, ошибки измерений, уровень IQ, давление, шум в радиосигналах – все это подчиняется закону Гаусса. К примеру:

• В любом виде спорта большинство результатов близки к среднему значению, а только единицы достигают экстремальных показателей (олимпийские рекорды). Если построить график всех пробежек на 100 метров среди спортсменов, он будет похож на колокол Гаусса.
• Если взять миллион случайных людей и измерить их рост, график получится колоколообразной формы – и он будет точно соответствовать этой формуле.

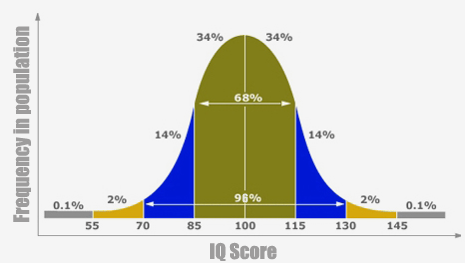
Формула была выведена Карлом Фридрихом Гауссом в 1810 году. Он заметил, что ошибки измерений астрономических объектов подчиняются этой закономерности. В дальнейшем оказалось, что формула нормального распределения отлично описывает хаос мира – от биологии до фондового рынка. Наш рост, оценки в школе, спортивные достижения, сигналы в смартфонах и даже ошибки ученых – все подчиняется этому закону.

Где мы встречаем нормальное распределение в жизни:

• Генетические особенности (рост, вес и даже уровень интеллекта) распределены по гауссовой кривой. Например, средний рост мужчин в мире – около 175 см, и большинство отклонений от этого значения предсказуемы с помощью формулы нормального распределения.
• Изменения цен на акции часто моделируются гауссовым распределением. Оно помогает трейдерам предсказывать вероятность резких скачков и падений цен.
• Помехи в радиосвязи описываются гауссовым распределением – это помогло инженерам в разработке Wi-Fi, 5G и спутниковой связи.

💡Интересные факты:

• Портрет Гаусса и кривая распределения украшали немецкие 10-марковые купюры в 80-х годах.

• В 2008 году кризис на Уолл-стрит был вызван тем, что финансисты неправильно применяли нормальное распределение к редким событиям (кризисам).

9. Преобразование Фурье

Формула Жозефа Фурье (1822) утверждает, что любой сложный сигнал можно представить как сумму простых синусоидальных волн. Возьмем, к примеру, музыку: любая песня состоит из низких, средних и высоких частот. Ухо их не разделяет, но преобразование Фурье способно разложить звуковой поток и показать отдельные ноты и их громкость. Если взять звук пианино и построить его спектр с помощью преобразования Фурье, мы увидим отдельные пики, соответствующие нотам.

Где применяется преобразование Фурье:

• MP3-сжатие и аудиофильтры работают с преобразованием Фурье. Именно оно помогает отделить басы от вокала и создавать эффекты, такие как авто-тюн.
• Wi-Fi сигнал кодируется и декодируется через преобразование Фурье, чтобы минимизировать потери информации. Без этой формулы интернет работал бы в 1000 раз медленнее, а радиосвязь была бы невозможна.
• Цифровые камеры применяют быстрое преобразование Фурье для сжатия изображения и устранения шумов.
• Магнитно-резонансная томография (МРТ) использует преобразование Фурье, чтобы из электромагнитных сигналов в теле создать точное изображение органов.
• Землетрясения вызывают сложные колебания земной коры, но с помощью преобразования Фурье можно выделить опасные частоты и предсказать разрушительные толчки.

💡Интересные факты:

• Если бы не преобразование Фурье, не было бы MP3, JPEG, МРТ, Wi-Fi и мобильной связи.
• Spotify и Shazam используют преобразование Фурье, чтобы узнавать песни по короткому фрагменту.

10. Уравнение Навье-Стокса

Это одно из основополагающих уравнений в механике жидкостей и газа: его применяют в аэродинамике, метеорологии, гидродинамике и моделировании климата.

Несмотря на свою кажущуюся простоту, уравнение является чрезвычайно сложным для аналитического решения, особенно в трехмерных ситуациях с турбулентными потоками.

Как используют уравнение Навье-Стокса:

• В аэродинамике уравнение Навье-Стокса позволяет моделировать и предсказывать поведение воздушных потоков вокруг летательных аппаратов, что важно для оптимизации их формы и повышения их эффективности. Например, при проектировании самолетов используется для анализа турбулентности, сопротивления и подъема.
• В метеорологии уравнение применяется для предсказания движения атмосферных потоков, что важно для составления прогноза погоды, изучения климатических изменений и моделирования глобальных погодных явлений (циклоны и антициклоны).
• В гидродинамике уравнение используется для описания течений жидкостей в инженерных задачах (проектирование трубопроводов, судов, водоемов и других систем), где важны характеристики движения жидкости.

💡Интересный факт

На данный момент еще не существует общего решения уравнений Навье-Стокса для всех возможных случаев, и для многих практических задач используются численные методы (например, метод конечных элементов или метод конечных разностей).

11. Уравнения Максвелла

Уравнения Максвелла, сформулированные в середине 19 века, описывают, как взаимодействуют электрические и магнитные поля. Они показывают, что эти поля не существуют изолированно, а всегда взаимосвязаны. Эти четыре уравнения объединяют явления электричества и магнетизма в одну теорию электромагнетизма, объясняя, как электрические поля создают магнитные поля и наоборот, как магнитные поля могут индуцировать электрические:

• Электрическое поле возникает вокруг электрических зарядов и может быть изменено изменениями в распределении зарядов.
• Магнитное поле возникает вокруг движущихся зарядов (токов) и изменяется с изменением тока или изменяющегося во времени электрического поля

Эти взаимодействия лежат в основе множества современных технологий, от радиоволн до оптики и беспроводной связи:

• Уравнения Максвелла описывают распространение электромагнитных волн, что является основой для всех современных технологий, использующих электрические и магнитные поля (радиосвязь, телевидение, мобильная связь и Wi-Fi).
• Электромагнитные волны, как описано в уравнениях Максвелла, являются основой для понимания света. Максвелл предсказал, что свет — это видимость электромагнитных волн, и его волновая природа была подтверждена позже.
• Уравнения Максвелла сыграли важную роль в развитии теории квантовой электродинамики (QED), которая описывает взаимодействия между светом (фотонами) и материей. QED является основой для понимания многих процессов в атомной и субатомной физике.
• Генерация и передача электричества на основе принципов электромагнитной индукции, как это описано в уравнениях Максвелла, являются основой для работы электростанций и трансформаторов.

Уравнения Максвелла можно выразить через четыре основных уравнения:

• Закон Гаусса (для электрического поля) – говорит о том, что поток электрического поля через замкнутую поверхность пропорционален суммарному электрическому заряду внутри этой поверхности.
• Закон Гаусса для магнитного поля – указывает, что магнитные поля не имеют источников или стоков, как электрические поля. То есть, магнитные поля всегда замкнуты: линии магнитного поля всегда образуют замкнутые контуры, и не существует магнитных монополей (отдельных северных или южных магнитных полюсов, в отличие от электрических зарядов).
• Закон индукции Фарадея – описывает, как изменяющееся во времени магнитное поле создает электрическое поле. Это явление лежит в основе работы генераторов и трансформаторов и является фундаментом для принципа электромагнитной индукции.
• Теорема о циркуляции магнитного поля (закон Ампера – Максвелла) – связывает магнитное поле с электрическим током и изменением электрического поля. Он описывает, как токи и изменяющиеся электрические поля создают магнитные поля.

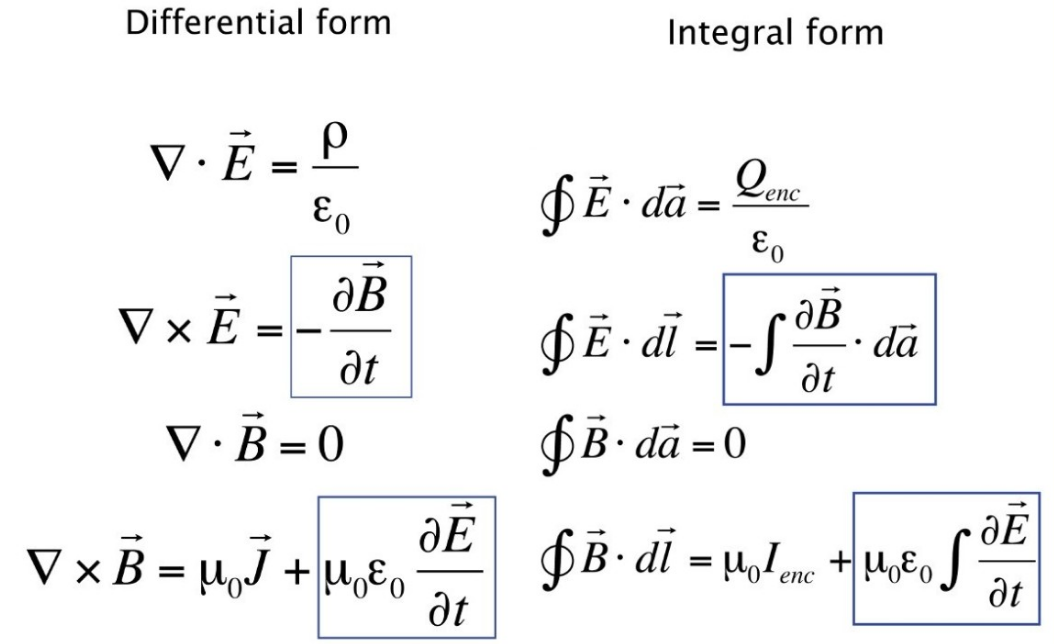
💡Интересный факт

Уравнения Максвелла оказали огромное влияние на развитие физики и технологий и стали краеугольным камнем для множества современных научных и инженерных дисциплин, включая электронику, радиотехнику, оптику и квантовую электродинамику.

12. Второй закон термодинамики

Это один из основополагающих законов физики, который играет важную роль в понимании процессов, происходящих во Вселенной, от простых физических явлений до сложных биологических и космологических процессов:

• В космологии второй закон термодинамики важен для объяснения конечности процессов, происходящих во Вселенной. Например, тепловая смерть Вселенной — гипотеза, согласно которой, если Вселенная продолжит расширяться, она может достичь состояния, в котором все объекты находятся в тепловом равновесии, и никакие полезные процессы не смогут происходить. Это будет максимальное состояние энтропии.
• В биологии второй закон объясняет, почему живые организмы должны поддерживать упорядоченность внутри себя (низкую энтропию), используя внешнюю энергию (например, пищу или свет). Организмы поддерживают порядок, но только за счет увеличения энтропии в окружающей среде.
• Применение второго закона критично в различных областях инженерии, таких как создание тепловых машин, холодильников и двигателей. В этих устройствах всегда существует некоторая потеря энергии (в виде тепла), что ограничивает их эффективность.

💡Интересный факт

Этот закон объясняет, почему природа стремится к состоянию максимального беспорядка или равновесия, и почему энергия всегда будет распределяться от более концентрированных областей к более рассеянным.

13. Эквивалентность массы и энергии

E = mc² – одна из самых известных формул в истории науки. Это уравнение, предложенное Альбертом Эйнштейном в 1905 году как часть его работы над специальной теорией относительности, показывает, что масса и энергия — это две формы одной и той же сущности, и каждая может быть превращена в другую. Это означает, что вся материя обладает потенциальной энергией, которую можно высвободить, если объект будет преобразован в чистую энергию.

Энергия, которую содержит объект, пропорциональна его массе, а коэффициент пропорциональности c² — это квадрат скорости света. Скорость света в вакууме является чрезвычайно большой величиной (299 792 458 м/с в секунду), поэтому даже относительно небольшая масса может быть преобразована в огромное количество энергии.

Как эквивалентность массы и энергии используется в реальной жизни:

• В процессе ядерной реакции (происходящей при взрыве ядерного оружия или при работе мирного ядерного реактора) масса атомного ядра превращается в огромную энергию в соответствии с уравнением Эйнштейна.
• В медицине это уравнение применяют в методах визуализации, например, в позитронно-эмиссионной томографии (ПЭТ), где античастицы (позитроны) встречаются с электронами, и в процессе их аннигиляции высвобождается энергия.
• До появления теории относительности ученые не могли объяснить, как звезды излучают энергию на протяжении миллиардов лет. Благодаря уравнению Эйнштейна стало понятно, что звезды не просто горят как топливо, а высвобождают энергию через ядерные реакции, где часть массы превращается в энергию.
• Уравнение Эйнштейна оказало огромное влияние на развитие астрофизики, особенно в области понимания энерговыделяющих процессов в космосе, гамма-всплесков, образования нейтронных звезд и черных дыр.

💡Интересные факты:

• В звездах, таких как наше Солнце, водород превращается в гелий в результате термоядерного синтеза, сопровождаемого высвобождением энергии согласно уравнению Эйнштейна.
• Когда массивная звезда исчерпывает свое ядерное топливо, она может взорваться как сверхновая. В ходе этого процесса часть массы звезды превращается в энергию (по E = mc²), высвобождая колоссальные количества энергии, которые могут превзойти светимость всей галактики.
• После взрыва сверхновой остается нейтронная звезда или черная дыра. В этих объектах вещество сжато до экстремальных плотностей, и преобразование массы в энергию играет ключевую роль в их формировании.
• В аккреционных дисках черных дыр материя падает внутрь и выделяет огромное количество энергии, что также объясняется формулой Эйнштейна.

14. Уравнение Шредингера

Это основное уравнение квантовой механики, которое описывает поведение микроскопических частиц, таких как электроны, атомы и молекулы. Оно является краеугольным камнем в квантовой теории и открывает новые горизонты для понимания мира на наноуровне, где классическая физика перестает работать.

Уравнение Шредингера, опубликованное в 1926 году, является описанием динамики квантовых систем. В отличие от классической механики, где объекты имеют определенные положения и скорости в каждый момент времени, в квантовой механике состояние частицы описывается не четко определенными значениями, а вероятностями:

• Волновая функция Ψ. Является центральным объектом квантовой механики. Волновая функция описывает вероятностное распределение всех возможных состояний системы в пространстве. Например, для электрона в атоме волновая функция дает вероятность нахождения электрона в определенной точке пространства.
• Гамильтониан H. Этот оператор связан с общей энергией системы и действует на волновую функцию. Он включает в себя как кинетическую энергию (связанную с движением частиц), так и потенциальную энергию (в зависимости от внешних сил, действующих на систему).

Где и как применяется уравнение Шредингера:

• Уравнение Шредингера позволило глубже понять строение атома. Например, квантовая теория атомов водорода, описанная этим уравнением, показала, что электроны существуют не как частицы, движущиеся по определенным орбитам, а как распределенные по вероятностным облакам. Эта теория объясняет спектры излучения атомов, что стало основой для развития квантовой химии.
• В квантовой химии уравнение Шредингера применяется для вычисления свойств молекул, таких как энергия, стабильность и структура. Это позволяет моделировать молекулы на атомарном уровне, что используется, например, в разработке новых лекарств и материалов.
• В теории квантовых компьютеров уравнение Шредингера описывает эволюцию квантовых битов (кубитов), которые могут быть в суперпозиции состояний. Это позволяет квантовым компьютерам выполнять определенные вычисления намного быстрее, чем классические компьютеры.
• В нанотехнологиях уравнение Шредингера используется для изучения поведения материалов на наноуровне, где квантовые эффекты, такие как туннелирование или квантовая суперпозиция, играют важную роль. Например, понимание того, как электроны ведут себя в наноразмерных структурах, помогает создавать более эффективные транзисторы и другие устройства.
• Квантовое туннелирование, когда частица проходит через потенциальный барьер, который в классической механике она не может преодолеть, объясняется с помощью уравнения Шредингера. Это явление используется в таких технологиях, как сканирующая туннельная микроскопия, которая позволяет «видеть» поверхности на атомарном уровне.

💡Интересные факты:

• Уравнение Шредингера изменило наше понимание мира на микроскопическом уровне. Оно не только объяснило странные и контринтуитивные явления квантовой механики, такие как суперпозиция состояний и туннелирование, но и стало основой для многих технологий, которые используются в современной науке и промышленности.
• Шредингер предложил знаменитую мысленную задачу — «Кот Шредингера», чтобы подчеркнуть странность квантового мира, где система может быть в нескольких состояниях одновременно.

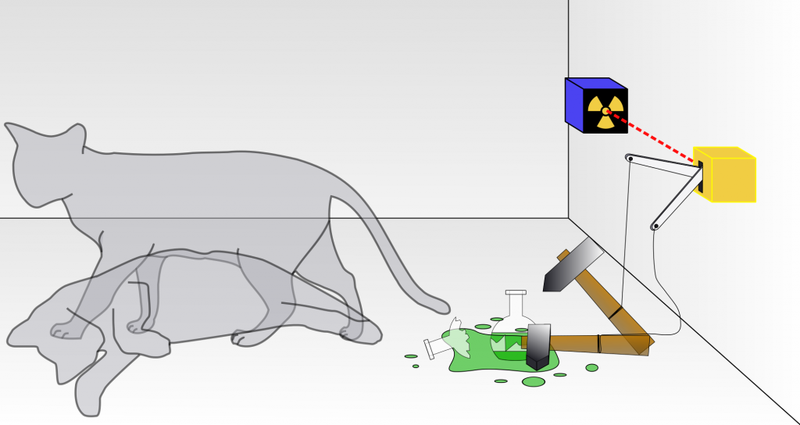
• Важность уравнения не ограничивается только физикой, так как оно также привело к революционным изменениям в философии науки, в том числе в понимании природы реальности, наблюдения и вероятности.

15. Теория информации

Формула, опубликованная Клодом Шенноном в работе «Математическая теория связи» в 1948 году, дала математическое определение понятию информации и установила основы для многих технологий, включая сжатие данных, криптографию, кодирование и передачу информации по каналам связи.

Эта формула описывает количество информации или энтропию, которую можно ожидать от случайного источника, генерирующего символы (например, буквы, цифры, события). Чем выше энтропия, тем больше неопределенности или неожиданности содержит источник:

• Если вероятности всех событий одинаковы, энтропия будет максимальной, потому что каждое событие максимально непредсказуемо.
• Если одно событие имеет вероятность 1, а все остальные имеют вероятность 0, энтропия равна нулю, потому что результат можно предсказать с полной уверенностью.

Где и как применяется теория информации:

• Формула Шеннона используется в сжатии данных (например, в алгоритмах код Хаффмана или Лемпеля-Зива-Вэлча). Если для каждого символа в сообщении вероятность появления этого символа известна, можно создать оптимальные коды для каждого символа, минимизируя количество битов, необходимых для передачи сообщения. Чем выше энтропия, тем более эффективное сжатие данных нужно для того, чтобы сохранить информацию, не теряя данных.
• В криптографии формула Шеннона используется для оценки безопасности криптосистемы. Чем выше энтропия ключа шифрования, тем сложнее будет предсказать или подобрать этот ключ с помощью криптоанализа. Например, если криптографическая система использует ключ, который обладает высокой энтропией, то вероятность его взлома становится чрезвычайно низкой.
• В теории передачи информации Шеннон установил основополагающее понятие, называемое пределом Шеннона. Это максимальная скорость передачи информации (или канальная пропускная способность), при которой информация может быть передана без ошибок через канал связи. Энтропия в этом контексте позволяет вычислить максимальную информацию, которую можно передать по каналу с ограниченной пропускной способностью.
• Перекрестная функция потерь, основанная на теории информации, используется для обучения нейросетей.
• Шенноновская энтропия применяется для анализа генетической информации и прогнозирования мутаций в генетике, и для изучения передачи сигналов между нейронами в нейробиологии.

💡Интересный факт

Благодаря формуле Шеннона мы получили математическое обоснование для изучения и оптимизации процессов передачи информации — фундаментальной основы развития технологий в цифровую эпоху.

16. Теория хаоса

Формула теории хаоса, которую Роберт Мэй представил в 1975 году, описывает эволюцию переменной x (например, численности популяции), которая изменяется на каждом шаге времени в зависимости от предыдущего значения x_t. Величина k – это параметр, который контролирует скорость роста популяции или динамику системы.

Чувствительность к начальным условиям и нелинейность взаимодействий приводит к тому, что системы могут развиваться по непредсказуемым траекториям, несмотря на наличие четких математических законов. Это явление имеет огромное значение в научных исследованиях, поскольку хаотическое поведение можно наблюдать в биологии, экономике, метеорологии и других дисциплинах:

• В биологии теория хаоса используется для описания популяционной динамики. Простая модель популяции с помощью уравнения логистического роста позволяет моделировать как может изменяться численность популяции животных или растений, например, в зависимости от доступных ресурсов. При определенных значениях параметров популяция может колебаться или даже вымереть.
• В прогнозировании погоды используется теория хаоса, так как атмосферные явления зависят от множества факторов, которые могут быть чрезвычайно чувствительны к начальным условиям. Это приводит к тому, что долгосрочные прогнозы погоды (например, на месяцы вперед) становятся невозможными.
• В экономике теория хаоса помогает моделировать поведение рынков и цен, которые могут быть подвержены нестабильности и непредсказуемым колебаниям. Например, изменения в спросе и предложении могут вызвать цепную реакцию, которая приведет к хаотичным изменениям на финансовых рынках.
• В климатологических моделях теории хаоса используются для прогнозирования изменений климата, включая глобальное потепление. Модели климата могут показать, как небольшие изменения в одной части системы могут повлиять на климатические условия в глобальном масштабе.

💡Интересный факт

Состояние системы может сильно изменяться в зависимости от начальных условий. Это явление хорошо известно в теории хаоса и называется эффектом бабочки, когда маленькие изменения на начальных этапах могут привести к кардинально различным результатам в будущем.

17. Модель Блэка-Шоулза

Модель Блэка-Шоулза — это формула, с помощью которой можно рассчитать справедливую цену опциона (финансового инструмента, дающего право купить или продать актив в будущем по заранее оговоренной цене). Эта модель произвела революцию в финансовой математике и принесла авторам Нобелевскую премию по экономике в 1997 году (правда, сам Фишер Блэк не дожил до награждения).

До появления этой модели трейдеры оценивали опционы интуитивно. Блэк и Шоулз дали рынку точный математический инструмент, который позволил управлять рисками и строить сложные финансовые стратегии. Благодаря этой модели:

• Появились деривативы как полноценный рынок.
• Хедж-фонды и инвестиционные банки начали активно использовать опционы.
• Волатильность стала ключевой характеристикой финансовых инструментов.

Чтобы уравнение работало, авторы ввели несколько важных допущений:

• Рынки идеальны — нет налогов, комиссий, и не бывает резких скачков цен.
• Нет арбитража — невозможно гарантированно зарабатывать без риска.
• Процентные ставки и волатильность фиксированы — не меняются во времени.
• Акции следуют геометрическому броуновскому движению — их цены изменяются случайно, но с предсказуемым средним ростом и волатильностью.

Эти предположения, конечно, далеки от реальности. Но, несмотря на допущения и ограничения, модель Блэка-Шоулза по-прежнему остается основой современного рынка деривативов. Это один из тех редких случаев, когда чистая математика изменила мир реальных денег.

💡Интересные факты:

• Хотя модель очень полезна, она не учитывает резкие скачки цен и рыночные паники. Например, 19 октября 1987 года произошел «Черный понедельник» — крах фондового рынка, когда цены упали так быстро, что модель Блэка-Шоулза перестала работать.
• В 1998 году хедж-фонд LTCM, который активно применял сложные стратегии, основанные на модели, потерпел крах, едва не обрушив мировую финансовую систему. Это показало, что реальный рынок сложнее, чем идеальная математическая модель.

В заключение

Каждая из представленных в нашей статье семнадцати концепций стала прорывом в человеческом познании и открыла новые горизонты в науке и технологиях. История каждого уравнения — это история человеческого гения, преодолевающего границы известного. Эти формулы не только описывают реальный мир: они позволяют нам преобразовывать его, создавая все — от небоскребов до квантовых компьютеров, от финансовых инструментов до космических кораблей.