Думаете, математика поможет решить все задачи и вопросы? А вот и нет! Смотрите, как она не справляется с толкованием некоторых вещей.

Даже математика не в силах объяснить отдельные невероятные явления. Предпочитаю называть эти вещи «Абракадаброй математики». В разработке тоже встречаются подобные загадки.
Изложенная информация будет наиболее интересна фронтендерам и заядлым любителям математики ;)
Любимое число
Давайте посмотрим на один такой трюк. Предположим, что вы учитесь в классе с численностью не менее 25 студентов, а я преподаватель. Даю каждому чистый лист бумаги и прошу написать цифру от 0 до 9 включительно. Когда вы справитесь и свернёте листок, соберу бумаги. Само собой, я не в курсе, что вы придумали. Тем не менее гарантирую, что буду знать число, которое встречается чаще других в ответах аудитории.
Теперь утверждаю, что большинство студентов выбрали цифру 7. Если учащийся придёт, посмотрит все листки и проверит, то скажет: «Вы правы! Но как?»
К сожалению, нет никакого объяснения такой закономерности, хотя она железная. Большинство людей всегда делают выбор в пользу цифры 7. Я мог сыграть в эту игру свыше 100 раз, и никогда бы не ошибся.
О данном фокусе мне рассказал один любимый профессор, Али Несин, 10 лет назад. Чтобы попробовать трюк, соблюдайте некоторые условия. Перво-наперво нужно как минимум 25 человек. В противном случае будет рискованно. Вы подумаете, что речь идёт о вероятности, но на самом деле это не так. Поскольку в задании 10 цифр, вероятность выбора любой составляет 1/10 для каждого учащегося. Итак, математическое толкование не работает здесь. Думаю, что это объясняется физиологией или социологией.
Красота
А также математика не способна истолковать другую чрезвычайно занимательную вещь. Здесь 4 разных прямоугольника. Спросите людей, какой красивее, и 70–80% выберут зелёный.
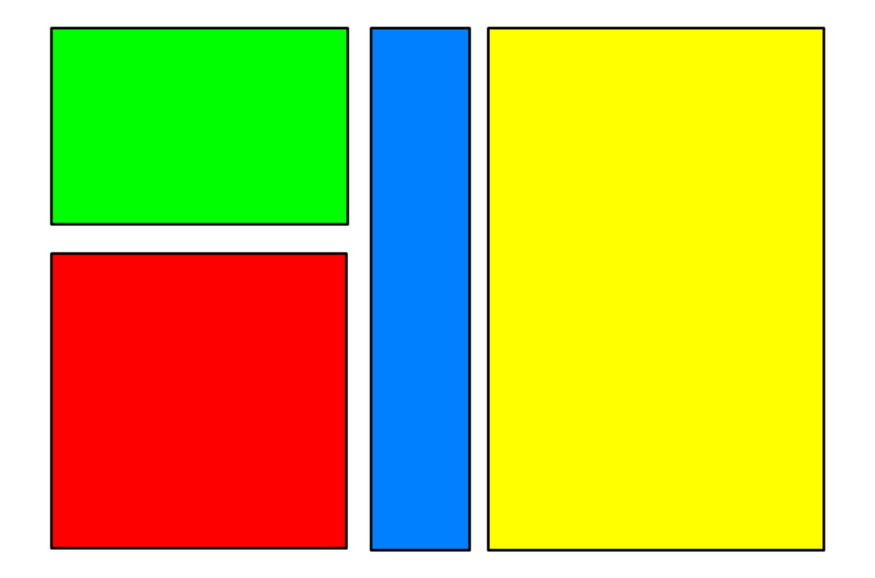
При этом не получится объяснить положение с использованием только математики, потому что в ней нет определения красоты, и этот факт математически непостижим. Впрочем, маркетологи использовали данную информацию вовсю. Когда поняли, что основная масса людей предпочитает определённый дизайн.
Спустя много лет мы так и не нашли ответ, почему люди выбирают число 7, но академик Адриан Беджан разобрался в причине выбора зелёного прямоугольника. Профессор обнаружил, что «человеческий глаз способен интерпретировать изображение на основе золотого сечения быстрее, чем любое другое».Таким образом, благодаря гармоничному делению прямоугольник зелёного цвета и выглядит красивее остальных фигур.
Вероятно, вы слышали об Евклиде. Этот математик написал книгу под названием «Элементы». Однозначно рекомендую вам купить том. В труде Евклид определил золотое сечение следующим образом:
Разделите прямую линию в крайнем и среднем отношении так, чтобы целая линия относилась к большему отрезку, как больший к меньшему.

Другими словами, Евклид говорил: на отрезке стоит точка, назовём её золотой, которая идеально разделяет линию. Он утверждал уверенно, но также и правдиво.
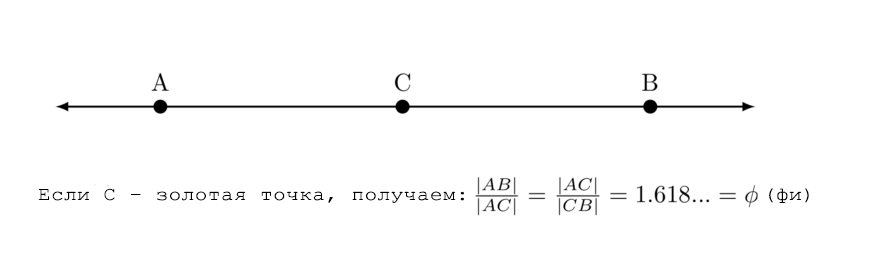
Теперь говорим математически, когда провели отрезок |AB|, и между A и B – точка C, то получаем соотношения |AB|/|AC| и |AC|/|BC|. Тогда равенство этих двух соотношений будет золотым сечением, 1,618…, φ (фи). Фи (/ faɪ /; заглавные Φ, строчные φ).
Уверен, что эта специальная пропорция вызывает море любопытства, и вам не терпится узнать, как Евклид получил значение золотого сечения? Давайте попробуем понять вместе.
Предположим что: длина |AC| = x и длина |CB| = y. Тогда
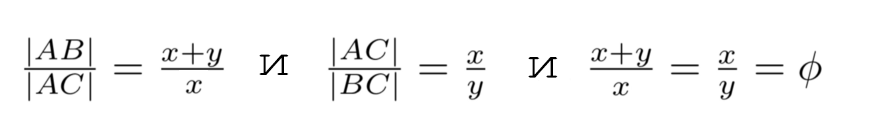
То есть если найдём значение x/y, то получим и величину φ, и это выведет нас на квадратное уравнение. Перемножим накрест – (x + y) на y и x на x – и получим: x² = xy + y² Затем перенесём переменные в одну сторону, и в этот раз результат будет такой: x² – xy + y² = 0 Напоминание: наша цель найти x/y. Итак, если разделить все члены на y², то получим:
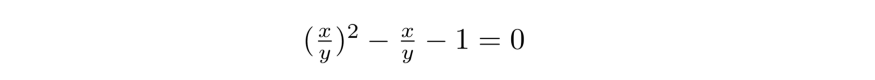
Когда определите (x/y) = φ, увидите: φ² – φ – 1 = 0. Здесь вспомните квадратичную формулу. Квадратичная формула: Пусть a, b и c – действительные числа. Решением ax² + bx + c = 0 будет:
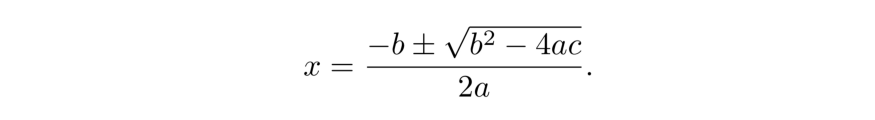
Квадратичная формула гласит, что произведение корней нашего уравнения (с/а) составляет –1. Таким образом, одно произведение корней отрицательно, а другое положительно. В то же время определение золотого сечения говорит: φ – неотрицательная величина. Значит, выбираем вариант со знаком «плюс». Теперь получится решить уравнение.
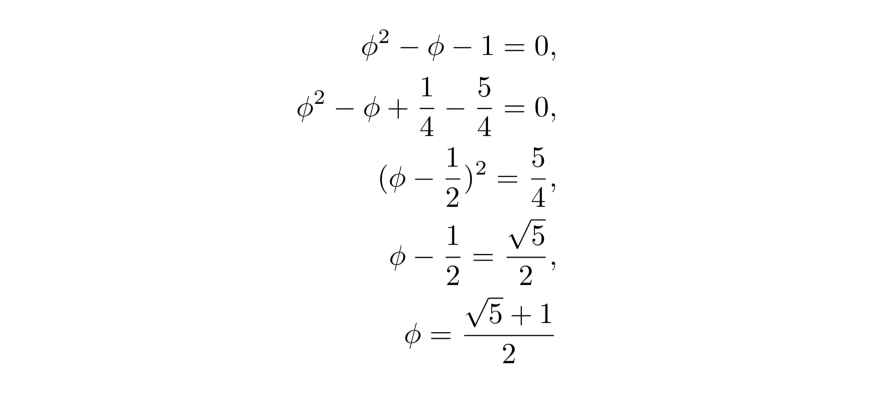
Пока что работали над отрезком. До сих пор готовимся показать, почему люди выбирают зелёный прямоугольник выше и на каком основании Евклид назвал его золотым.
Когда вернёмся к нашему отрезку |AB| с точкой C, согнём его в золотой точке C, то получим прямой угол. Теперь построим прямоугольник. Он будет золотым, потому что длины сторон равны x и y, и как уже показали, x/y представляет собой золотое сечение φ.
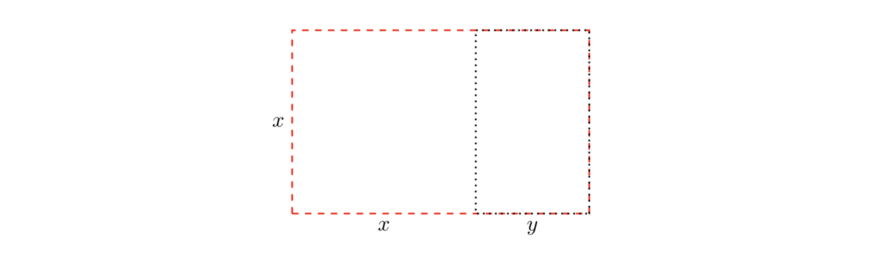
Золотой прямоугольник отличает свойство, которого нет ни у одного прямоугольника. В чём исключительность: если вырезать из него квадратную часть, оставшийся прямоугольник также золотой. Пусть это будет вам в качестве упражнения!
Непревзойдённый треугольник
Это ещё куда ни шло. Теперь попробуем другую задачу. Например, найти золотой треугольник, если такой существует.
Сначала решим, какой тип нужен для работы. Помните, когда удаляем квадратную часть из золотого прямоугольника, по-прежнему остаётся золотой прямоугольник. Нужно то же свойство для треугольников. Думаю, очевидно, что равносторонний не подходит, потому как при вырезании равностороннего треугольника из равностороннего треугольника остальная часть не будет такой же фигурой.
Тем не менее порадую тем, что возьмём равнобедренный треугольник. Шаги понятны. Берём его, а затем вырежем ещё один равнобедренный треугольник из нашего исходного, и проверим, будет ли оставшийся похож на первоначальный или нет. Если да, сделаем попытку назвать его золотым. А попробуем, потому что следующим шагом будет поиск соотношения сторон, равного золотому сечению.
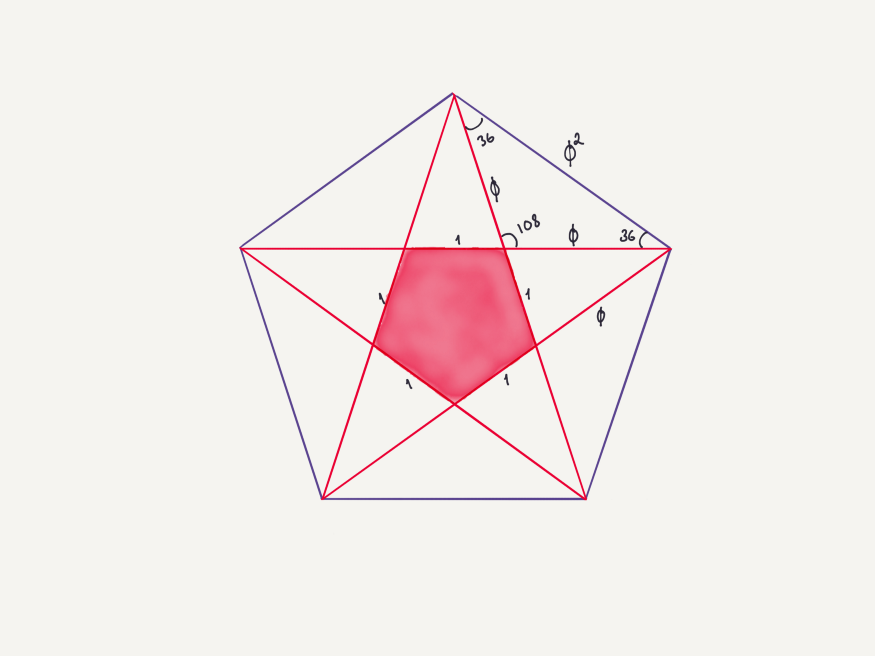
Начнём с равнобедренного треугольника ABC с углами при основании величиной 2α. Затем рисуем линию от точки B к стороне |AC|, чтобы получить два равнобедренных треугольника ABD и BCD. Результат захватывает: углы при основании треугольника BCD также равны 2α, а такие же углы у ABD – α, потому что сумма двух внутренних углов даёт внешний. Таким образом, углы треугольника ABC – α, 2α, 2α. Получаем 5α = 180 и α = 36.
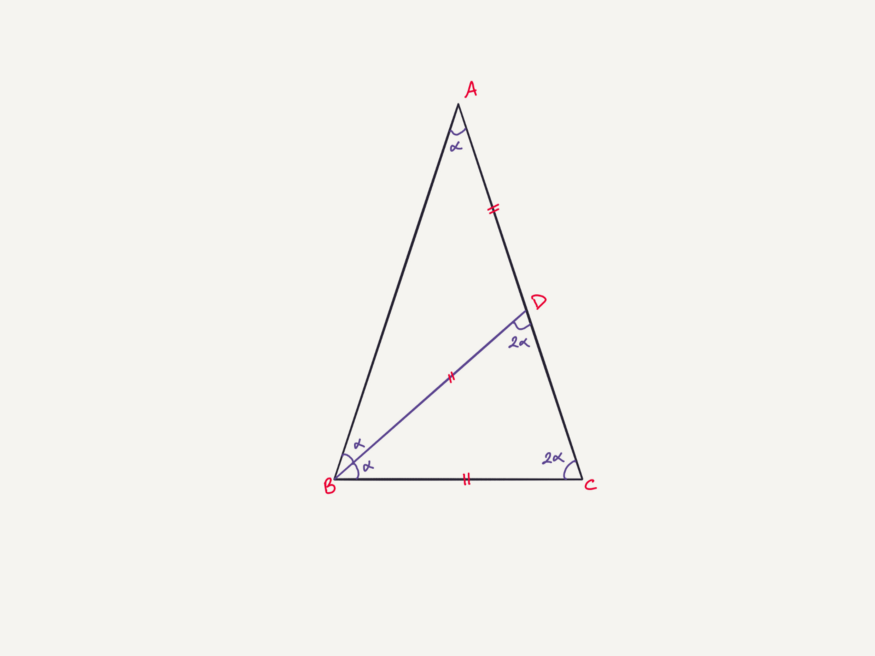
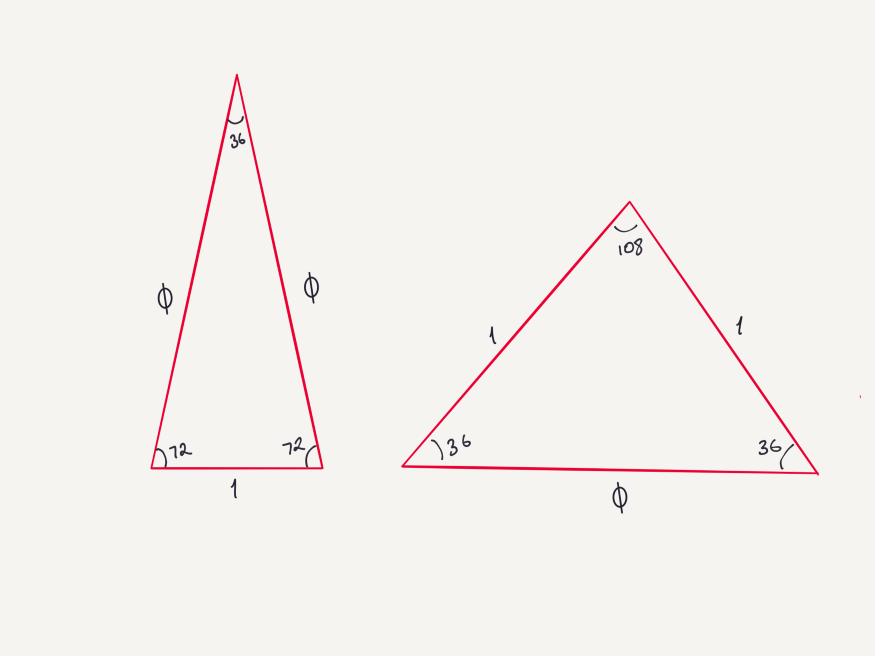
И вот мы нашли крайне специфический треугольник с верхним углом 36 и углами при основании 72.
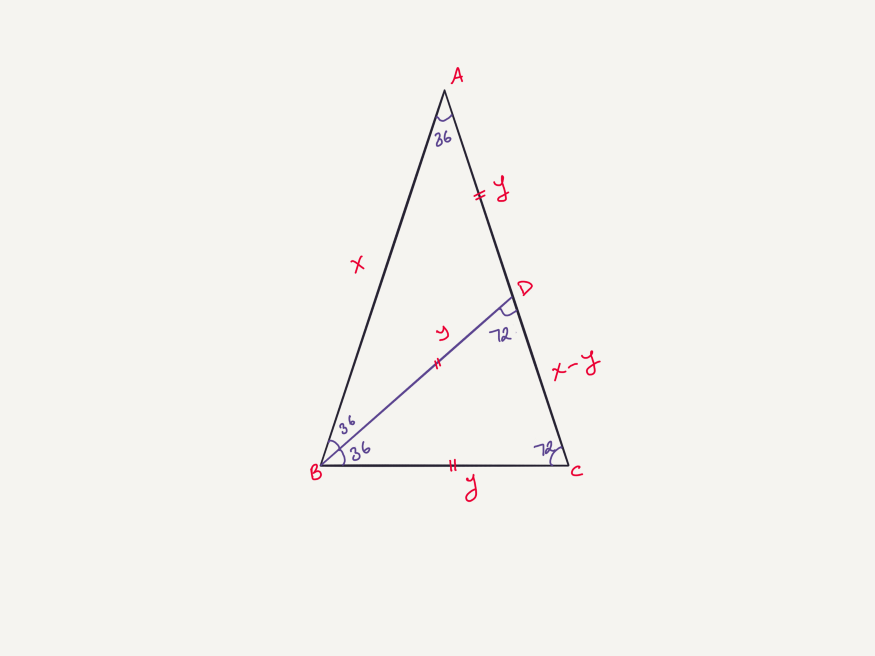
Для второго шага проверьте соотношение длин фигуры. Говоря |AB| = |AC| = x и |BC| = y, получим: |AD| = |BD| = y и |CD| = x – у И цель – найти x/у = φ или нет. Из подобия находим:
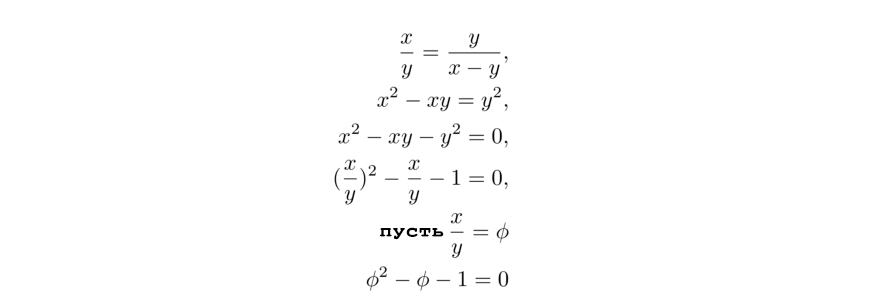
Как видите, получаем то же квадратное уравнение в конце. Таким образом, треугольник с углами 36–72–72 заслуживает названия «золотой». Кстати, когда продолжите углубляться, вы увидите, что 108–36–36 – также золотой треугольник. Эта информация будет полезна при работе с пятиугольником.
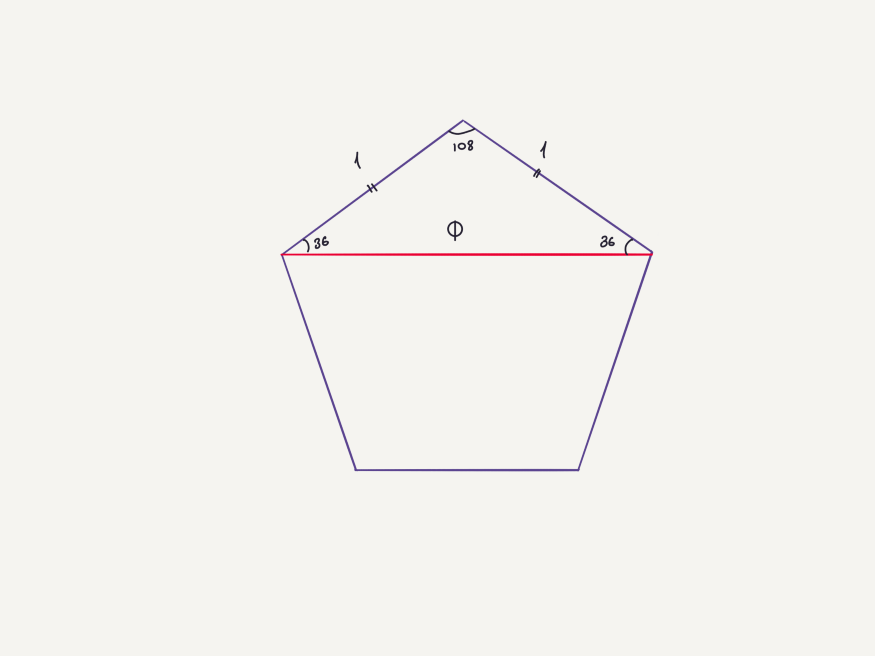
Исключительный пятиугольник
Рассмотрим другой пример. Изобразите пятиугольник, каково соотношение между длинами его диагонали и стороны? Если вы нарисуете диагональ с любого края, то получите золотой треугольник, потому что углы будут 108, 36 и 36. Итак, когда длина одной стороны пятиугольника равна 1, то длина диагонали равняется φ.
Мы решили сложный вопрос без математики. Когда не знаем о золотом сечении, приходится справляться с кучей линий, квадратными уравнениями и подобным.
Исследуйте ещё один пример. Нарисуйте все диагонали пятиугольника и получите несравненный результат. Посередине будет меньший пятиугольник, и каждый видимый треугольник окажется золотым.
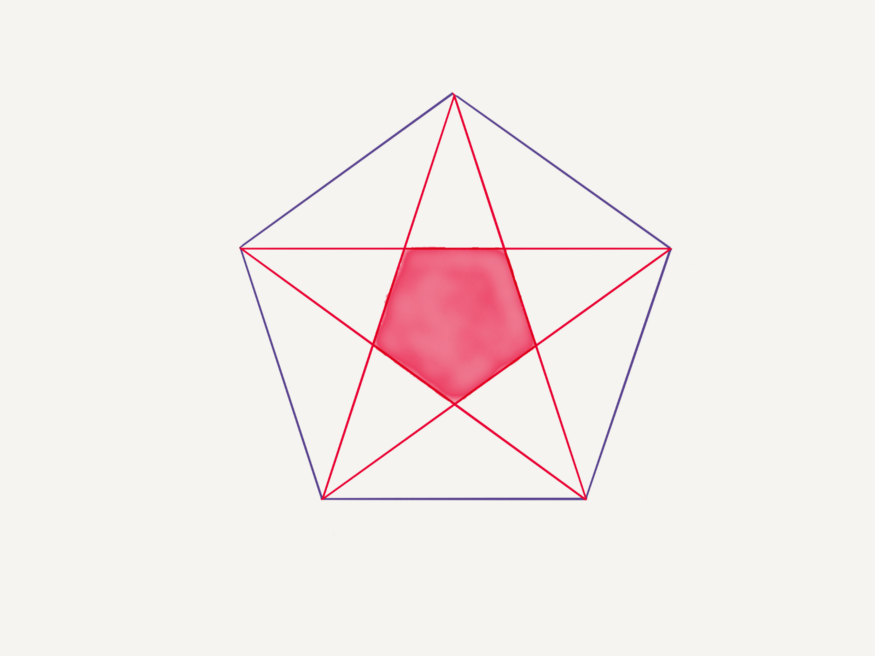
Вот вопрос: каково соотношение площади маленького пятиугольника к площади большого? Это легко решить, когда примем одну сторону небольшого пятиугольника за 1. Тогда длина другой стороны маленьких треугольников будет φ. И то же отношение подскажет, что длина основания треугольника равна φ². Теперь поможет подобие. Коэффициент подобия составляет 1/φ², а соотношение площадей будет 1/φ⁴.
Удивительное качество φ
А также отметим ещё одно отличительное свойство φ. Вернитесь и вспомните квадратное уравнение φ.
φ² – φ – 1 = 0, так что это даст: φ² = φ + 1
φ – единственное число, квадрат которого равен сумме самого себя и 1. Нет такого действительного числа, чтобы при добавлении к нему 1 вы увидели квадрат этого числа. И что любопытно, получаем такое:
φ² = 1φ + 1 φ³ = 2φ + 1 φ⁴ = 3φ + 2 φ⁵ = 5φ + 3 φ⁶ = 8φ + 5 ...
Вот примечательные постоянные числа. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… Они не случайные, а происходят из ряда Фибоначчи, где каждый член – сумма двух предыдущих.
Связь между последовательностью Фибоначчи и золотой пропорцией беспрецедентна. Отношение двух идущих друг за другом чисел из ряда приобретает золотое сечение через некоторое время. Вы получите эту пропорцию из каждой цифры, когда возьмёте большое число из последовательности.
Например, 5/3 = 1,666... 8/5 = 1,6 13/8 = 1,61... 21/13 = 1,618...
Продолжайте вычислять и получите новое число с φ.
Данная информация полезна, потому что помогает легко найти sin 18 или cos 36 без калькулятора. Это тоже упражнение для вас!



Комментарии