Иллюстративный видеокурс математического анализа через понятную анимацию визуализирует образы интегралов, пределов и производных.
В продолжение серии обзоров иллюстративных видеокурсов по математике, сделанных выпускником Стэнфорда Грантом Сандерсоном, в этой статье дается обзор курса математического анализа. Так же, как и в случае с линейной алгеброй, этот курс не содержит строгих доказательств, но позволяет представить образы, которые обычно сложно представить наглядно при прохождении классического курса математического анализа в институте. Рассмотрение любых моделей, основанных на малых приращениях, полезно иллюстрировать анимацией, а не статичными изображениями. Некоторые идеи, дающиеся обычно в алгебраической терминологии, в этом видеокурсе описываются более наглядно.
Курс состоит из 10 видеоуроков по 15-20 минут каждый. В качестве бонуса мы приложили видеоурок того же автора по преобразованию Фурье, к которому редакция proglib.io подготовила русские субтитры.
1. Введение курса. Основы математического анализа
https://www.youtube.com/watch?v=WUvTyaaNkzM
В вводном видео к иллюстративному курсу по математическом анализу дается обзор десяти уроков, из которых состоит курс, а также рассматривается одна из классических геометрических задач: нахождение выражения для определения площади круга радиуса R. Показывается, как известная из школьного курса геометрии формула S = πR2 может быть выведена из соображений симметричного разбиения круга на множество вложенных друг в друга колец.
Иллюстрируется один из основных подходов математического анализа: сложная проблема может быть представлена как сумма множества малых, легко определяемых значений. Такой подход позволяет, как это подтверждают следующие примеры, определить площадь под графиком любой функции. В заключение даются предварительные соображения об Основной теореме анализа.
2. Парадокс производной
https://www.youtube.com/watch?v=9vKqVkMQHKk
Во втором уроке вводится понятие производной как мгновенного изменения функции относительно ее аргумента. На множестве примеров визуализируется классическое рассмотрение движения автомобиля и его скорости как производной функции пройденного пути.
Рассматривается сложность вопроса мгновенной скорости – ведь для определения скорости необходимы две точки, пусть и расположенные максимально близко по времени. Умаляя разницу между этими точками до бесконечно малой величины, можно найти значение производной, описывающей наклон графика в этой точке по отношению к оси аргумента. Поясняется запись вида ds/dt. Рассматривается парадокс: можно ли считать движущимся объект в нулевой момент времени, относительно которого начинается движение?
3. Формулы производных через геометрические соображения
https://www.youtube.com/watch?v=S0_qX4VJhMQ
После предыдущего видео возникает вопрос: как вычислять производные для функций общего вида? У тех же, кто проходил курс математического анализа, может возникнуть вопрос посложнее: почему основное время практических занятий тратится на рассмотрение абстрактных функций вместо той же задачи о вычислении скорости реального объекта.
Полиномиальные, тригонометрические и показательные функции лежат в основе физических моделей, описывающих физический мир. Задача этого видео – дать представление о производных при помощи рассмотрения малых приращений функций x2 и x3 как приращений площадей и объемов.
Результаты рассуждений распространяются на полиномы более высоких степеней, и выводится общая формула определения производной степенной функции. Объясняется, как соотносятся геометрический и алгебраический подход. Геометрический подход позволяет представить аналогичным образом производные функций 1/x, sin(θ).
4. Визуализация дифференцирования сложных функций
https://www.youtube.com/watch?v=YG15m2VwSjA
В этом видео последовательно иллюстрируются правила взятия производных от суммы и произведения двух функций, а также процедура дифференцирования сложных функций, когда одна функция «вложена» в другую. В качестве примеров складываемых, перемножаемых и вложенных друг в друга функций рассматриваются sin(x) и x2.
5. Производные показательных функций
https://www.youtube.com/watch?v=m2MIpDrF7Es
В пятом видеоуроке иллюстрируется процедура взятия производных от показательных функций вида ax и ex. На примере роста популяции в зависимости от времени, описываемого выражением 2t, показывается, что скорость нарастания популяции пропорциональна самой функции.
Объясняется, почему коэффициент пропорциональности представляет собой натуральный логарифм от основания, и почему производная экспоненты равна самой экспоненте. Для этого достаточно лишь применить известные правила работы с показательными функциями. В заключение видео показывается пара примеров из физики и финансов, описываемых в терминах простейших дифференциальных уравнений, решениями которых являются экспоненциальные функции.
6. Производная функции, заданной неявно
https://www.youtube.com/watch?v=qb40J4N1fa4
Особо трудным моментом для детального понимания обычно является взятие производных от неявно заданных функций. Иллюстрация начинается с рассмотрения записи выражения линии, описывающей окружность x2 + y2 = 52. В этом случае производная находится обычно несколько механистически и напоминает взятие производной функции нескольких переменных.
Чтобы объяснить используемую процедуру, автор переходит к физическому примеру со скользящей относительно стены наклонной лестницей длиной 5 м. Такой подход позволяет лучше прочувствовать понятие производной для той же функции.
Та же задача решается на примере нахождения производной для sin(x)⋅y2 = x. В конце видео объясняется, как, пользуясь той же методологией выделения dy и dx, доказать, что производная натурального логарифма ln(x) это 1/x.
7. Пределы
https://www.youtube.com/watch?v=kfF40MiS7zA
Подспудно до этого при описании производных уже было задействовано понятие предела. В этом же видеоуроке гораздо лучше иллюстрируются такие аспекты:
- формальное определение производной;
- определение предела в терминах ε и δ;
- правило Лопиталя.
При описании терминологии ε и δ иллюстрируются причины требований к непрерывности функции и трудности, связанные с функциями, имеющими разрыв. Объясняются сложности взятия производных у функций, подобных sin(x)/x, и разрешения соответствующих неопределенностей.
8. Интегрирование и Основная теорема анализа
https://www.youtube.com/watch?v=rfG8ce4nNh0&t
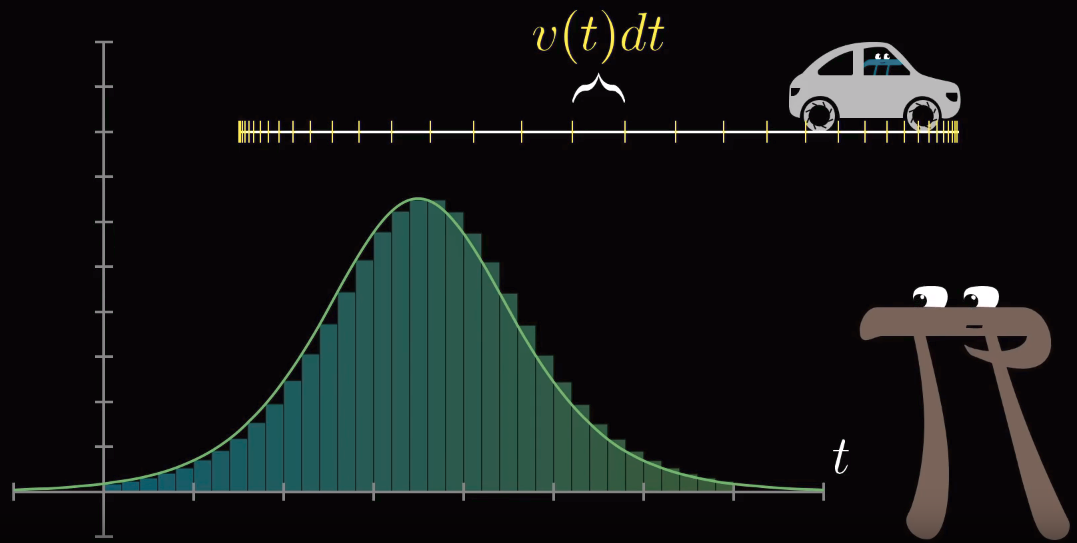
Можно ли узнать пройденный машиной путь только по наблюдениям спидометра? Эта задача обратна задаче о производной, обсуждавшейся во втором уроке видеокурса. Случай постоянной скорости становится основой для приближения переменной скорости как множества малых временных интервалов с различными скоростями. В результате вводится понятие интеграла.
Показывается, как интуитивным образом, представляя интеграл как «антипроизводную», можно найти первообразные функций. В конце видео рассказывается о важности учета не только самих площадей, но и их «знака» – того, как интегрируемые площади под функцией расположены относительно оси ординат.
9. Связь между площадью и наклоном
https://www.youtube.com/watch?v=FnJqaIESC2s
В девятом видеоуроке на примере гармонической функции рассматривается определение среднего значения функции на заданном интервале при помощи интегрирования. Выводится соответствующее выражение. Через площадь и наклон графиков тригонометрических функций показывается, как геометрически соотносятся понятия интеграла и производной. В видео также соотнесены понятия среднего значения функции и арифметического среднего.
10. Предварительные замечания. Производные высших порядков
https://www.youtube.com/watch?v=BLkz5LGWihw
Перед рассказом о ряде Тейлора необходимо поговорить о производных высших порядков, то есть производных от производных. В этом видео иллюстрируется процесс многократного дифференцирования различных зависимостей. Приводятся принятые обозначения таких дифференциалов. В примере с движением автомобиля вторая производная от дистанции по времени соответствует ускорению автомобиля.
10. Ряд Тейлора
https://www.youtube.com/watch?v=3d6DsjIBzJ4
Представление функции при помощи математического ряда степенных функций позволяет найти ее удобную аппроксимацию, ускоряющую вычисления с наперед заданной точностью, определяемой числом слагаемых такого ряда.
Начав с задачи представления гармонического движения маятника при помощи аппроксимации cos(θ) ≈ 1 – 1/2 θ2, автор иллюстрирует, как это решение можно было бы найти через подбор соответствующего полинома.
Рассматривается вопрос точности аппроксимации и то, как она повышается следующими членами ряда. Поясняется причина возникновения факториалов в формуле Тейлора и изменение формулы при разложении функции в ряд в смещенной точке.
Рассматриваются примеры разложений различных функций сложной функции в нескольких точках. Дается геометрическая иллюстрация аппроксимации функций несколькими первыми членами ряда. В завершение видео на примере разложения в ряд натурального логарифма затрагивается понятие круга сходимости (radius of convergence).
Бонус. Преобразование Фурье
https://www.youtube.com/watch?v=spUNpyF58BY
В качестве бонуса к представленному видеокурсу мы добавили урок о преобразовании Фурье, которое часто рассматривается в курсе математического анализа в институтах. Это преобразование основано на интегрировании комплексной переменной.
В данном видео дается оригинальная идея описания преобразования Фурье через построение особой математической машины, позволяющей разложить протяженный во времени сигнал по «чистым» одночастотным гармоническим функциям.
Для удобства восприятия сложного материала к этому видео редакция proglib.io подготовила русские субтитры.



Комментарии