☕ Хеш-таблицы в Java: секреты производительности

Всем привет! Меня зовут Миша Рокс, я – разработчик в Яндексе, и сегодня мы глубже погрузимся в одну из основных и базовых структур данных любого языка – хеш-таблицу. Конкретно – мы посмотрим на проблемы, которые возникают при имплементации этой структуры данных, когда сложность добавления или удаления из нее не O(1), а линейная, и какие потенциальные атаки можно провести на эту структуру данных (и как их избегают в современных языках программирования на примере Java).

Как работает хеш-таблица

В общем идейном случае, хеш-таблица – это 2D-структура данных. Ее можно представить как List<List<X>>, где X – это ваш тип данных. Внешний List – изначально фиксированной длины, и раздувается, и сужается в зависимости от условия, привязанного к общему количеству элементов во всей хеш-таблице (схоже с тем, как динамический массив увеличивается и уменьшается в размере в зависимости от количества элементов в нём).

Внешний List состоит из Внутренних List-ов, которые называются «Бакетами» (вёдрами по-русски :D), и каждый из бакетов – это просто коллекция типа X, например, список.

Когда вы вызываете .add(x) на хеш-таблице, внутренности имплементации считают hashcode от переданного x (а в случае Джавы – это происходит с помощью дёрганья метода .hashcode на объекте, поэтому и рекомендуют этот метод переопределять), относительно этого хешкода будет выбран конкретный бакет, и переданный элемент x будет добавлен в этот бакет (если бакеты – листы, то просто будет .add в конец листа).

Далее, когда вы хотите найти элемент в хеш-таблице, вы делаете .get(x) (или contains, или containsKey, т. д.), и хеш-таблица берет хешкод от x, определяет бакет, в котором этот элемент будет искать (т. к. когда элемент клали, бакет определялся по хешкоду, и требуемое свойство хеш-функции – это что для одного и того же x хешкод должен быть одним и тем же), и после получения бакета, ищет этот элемент в нём (в случае бакета – динамического массива – просто проходится по всем элементам и делает .equals. И поэтому в Джаве советуют переопределять .equals – потому что дефолтная имплементация .equals сравнивает объекты через == (то есть по значению ссылки), и два объекта с равными полями но разными ссылками не будут ==).

В этом алгоритме возникает понятная проблема – если:

1. Кол-во бакетов изначально задано константно (назовем это число C)
2. При добавлении 1.000.000.000 элементов, в лучшем случае максимальное количество элементов в каждом массиве будет 1.000.000.000 / C – если все элементы равномерно распределены по C бакетам, а в худшем – вообще все элементы попадут в один бакет, и там будет 1.000.000.000 элементов!
3. При поиске элемента в таких бакетах, worst-case сценарий в первом случае будет 1.000.000.000 / C операций, а во втором – вообще 1.000.000.000 операций! Это совсем не константная сложность, она прямо растёт с кол-вом элементов во всей хеш-таблице!

Но нам надо как-то гарантировать, что сложность будет константной (или хотя бы максимально приблизиться к таким гарантиям, потому что сейчас у нас Time Complexity гарантировано линейная). Этого можно достичь, расширяя внешний List – то есть, увеличивая количество бакетов.

Пусть изначально C == 10, тогда самый простой алгоритм (который не используется на практике, но имеет право на жизнь) – это увеличивать количество бакетов в 2 раза каждый раз, когда суммарное количество элементов во всей хеш-таблице достигнет C * K, где К – это тоже некая константа. При наличии «хорошей хеш-функции», которая условно говоря равномерно распределит значения .hashcode % C между всеми значениями [0; C-1], то в каждом бакете, ожидается, будет приблизительно K элементов.

Важный аспект – когда происходит увеличение количества бакетов с 10 до 20 (в этом примере мы делаем x2 бакетов), мы не можем просто оставить уже ныне имеющиеся элементы в бакетах [0, 9], потому что до «расширения» у каждого из элементов бакет определялся по функции hashcode % 10 (т. к. хешкод – это обычно значение, не ограниченное сверху, то оно может быть много больше 10, например, у какого-то из объектов функция могла быть 2523542345 % 10), а теперь C стало равно 20, и для тех же объектов значения hashcode % 10 не будут равны значениям hashcode % 20. То есть все элементы, которые уже есть во всей хеш-таблице, надо «перелить» из внешнего List-а размером 10 во внешний List размером 20.

Так как добавление одного элемента – это подсчёт хеш-кода (const Time Complexity) + добавление в бакет (если бакеты – листы – const Time Complexity), и элементов в хеш-таблице N, то вся операция «перелива» – это (const + const) * N, то есть – линейная Time Complexity относительно общего количества элементов в хеш-таблице. При добавлении еще x2 элементов в хеш-таблицу, ее еще раз надо будет раздувать, но если посмотреть на суммарное количество операций, требующихся на добавление элементов + раздувание при M-раздуваниях, будет видно, что общее количество операций = const * N, где N – это общее количество элементов в хеш-таблице, и в среднем на одно добавление требуется const операций. «Среднее количество операций over N runs» – называется Амортизационным анализом. То есть добавление в хеш-таблицу – это const Time Complexity по Амортизационному Анализу, но O(N) по ассимптотическому worst-case scenario анализу, потому что в худшем случае надо перелить N элементов.

Соответственно, если мы удаляем элементы из хеш-таблицы, надо ее обратно сдуть, например, с 20 до 10, если количество элементов стало намного меньше C * K, чтобы более оптимально использовать место внешнего List-а. Но вы уже видите проблему с этим подходом в случае нашего x2 алгоритма?) Можно найти такой «граничный» элемент, добавляя который хеш-таблица будет раздуваться, а убирая который – будет сдуваться, и каждый такой .add и .remove будет O(N) операцией, и если в хеш-таблице уже 1.000.000.000 элементов, это очень сильно ударит по перформансу программы.

Бороться с этим можно несколькими путями, один из них – делать разные «граничные числа сдувания и раздувания» так, чтобы между числом сдувания (меньшим числом) и числом раздувания для нынешнего размера внешнего Листа N, было (С / const) элементов, например, если у нас сейчас 400 бакетов в хеш-таблице (С == 400), K == 10, то есть Total элементов в хеш-таблице == 4000, чтобы граница раздутия была при 4200, а сдутия – при 3800. Когда бакетов будет 800, пусть граница раздутия будет при 8400, а сдутия – 7600, тогда худший вариант – за C операций добавления / удаления будет выполняться N * const суммарное количество операций, тогда каждая операция будет в среднем стоить K действий, а K == const, как вы помните.

Другой способ бороться с этим – это то, как сделано в дефолтных имплементациях хеш-таблиц в Java – это просто не сдувать внешний List вообще никогда. То есть если вы заполните HashSet 1.000.000.000 элементов в Java, а потом удалите все элементы, у вас останется огромный внешний List, без элементов во внутренних листах (вместо листов будут null, но внешний List будет огромным)

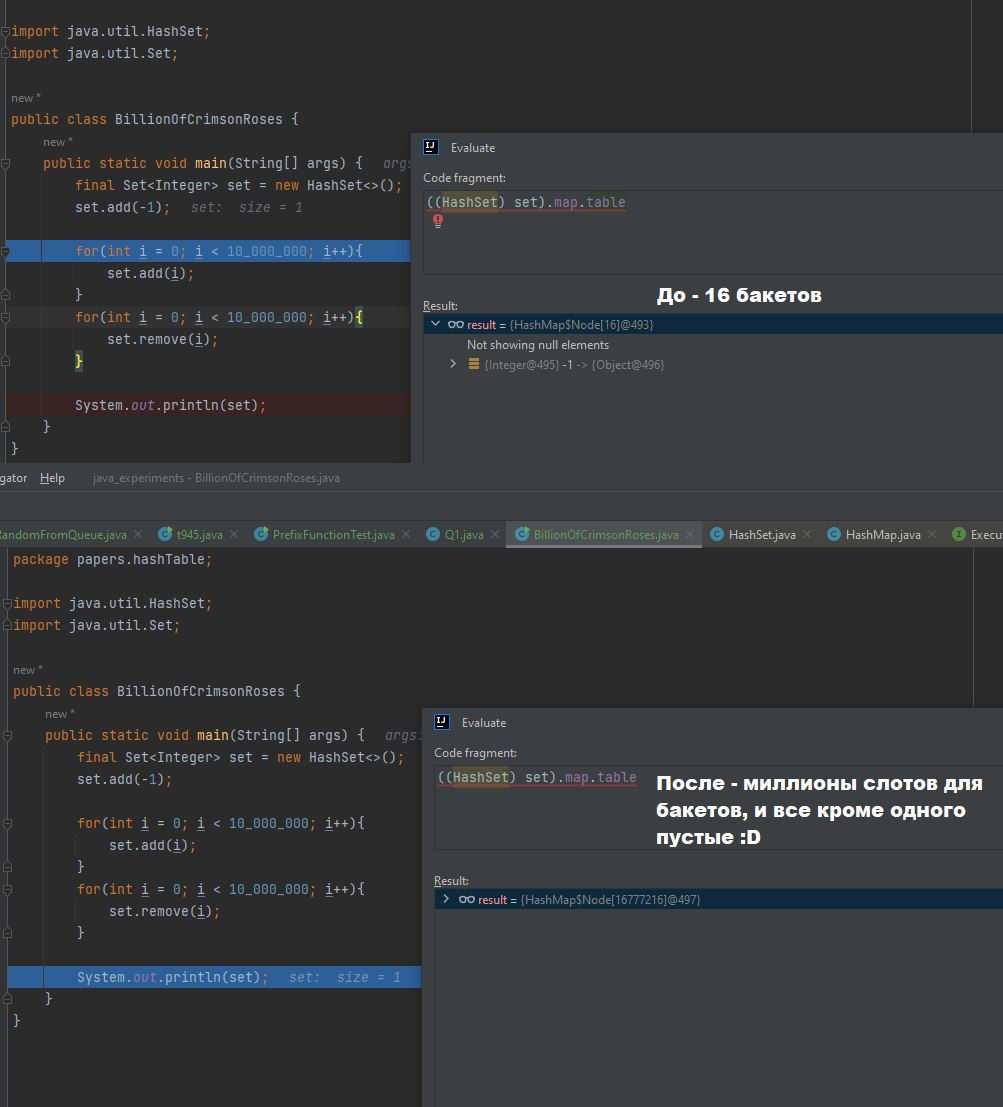
Вот так вот, люди, Оверрайдить equals и hashcode не обязательно, но если собираетесь класть ваш объект в структуру, использующую хеш, то это нужно, чтобы вы свой объект вообще могли из нее достать потом))

Лайк, шер, сабскрайб)