Изучение алгоритмов сортировки на языке Java поможет не изобретать велосипеды и быстро выскочить на лесенку карьерного роста.

Задействование алгоритмов сортировки поможет нам упорядочить массивы Java. Для понимания: сортировка чисел от наименьшего к большему или наоборот, а также лексикографический порядок – это примеры алгоритмов сортировки, способные упорядочить Java строки и числа

Сортировка пузырьком

Слышали о сортировке пузырьком? Его популярность обусловлена простотой, наглядностью и, конечно, названием.

Алгоритм просматривает массив и сравнивает каждую пару соседних элементов. Когда он встречает пару элементов, расположенных не по порядку, происходит замена двух элементов местами.

Остается вопрос: как узнать, что все элементы упорядочены? В этом случае очередная итерация пройдет без замены соседних элементов.

Вот шаги для сортировки массива чисел от наименьшего к большему:

• 4 2 1 5 3: два первых элемента расположены в массиве в неверном порядке. Меняем их.
• 2 4 1 5 3: вторая пара элементов тоже «не в порядке». Меняем и их.
• 2 1 4 5 3: а эти два элемента в верном порядке (4 < 5), поэтому оставляем как есть.
• 2 1 4 5 3: очередная замена.
• 2 1 4 3 5: результат после одной итерации.

Для полной сортировки нужен еще один шаг. Третья итерация пройдет уже без замены. Так вы поймете, что массив отсортирован.

Но причём тут пузырьки? Посмотрите снова на пример, и вы увидите, что алгоритм как бы смещается вправо. По этому поведению элементов в массиве и возникла аналогия с «пузырьками», всплывающими на «поверхность».

Реализация

Функция входит в цикл while, в котором проходит весь массив и меняет элементы местами при необходимости.

Массив в алгоритме считается отсортированным. При первой замене доказывается обратное и запускается еще одна итерация.

Цикл останавливается, когда все пары элементов в массиве пропускаются без замен:

public static void bubbleSort(int[] array) {  
    boolean sorted = false;
    int temp;
    while(!sorted) {
        sorted = true;
        for (int i = 0; i < array.length - 1; i++) {
            if (array[i] > array[i+1]) {
                temp = array[i];
                array[i] = array[i+1];
                array[i+1] = temp;
                sorted = false;
            }
        }
    }
}

Будьте осторожны с формулировкой условия замены!

Например, при условии a[i] >= a[i+1] алгоритм войдет в бесконечный цикл, потому что для равных элементов это условие остается true: отсюда следует бесконечная замена

Временная сложность

Рассмотрим наихудший сценарий. Вот в чем вопрос: сколько итераций нужно для сортировки всего массива? Пример:

5 4 3 2 1

При первой итерации 5 «всплывает на поверхность», при этом остальные элементы остаются в порядке убывания. Если вы хотите получить отсортированный массив, придется делать по одной итерации для каждого элемента, кроме 1, и еще одну итерацию для проверки, что в сумме составляет 5 итераций.

Расширьте это утверждение для массива из n элементов, и получите n итераций. В коде это означает, что цикл while будет запускаться максимум n раз.

Каждая n-ая итерация по всему массиву (цикл for в коде) означает, что временная сложность в наихудшем случае будет равна O(n ^ 2).

Сортировка вставками

Этот алгоритм разделяет оригинальный массив на сортированный и несортированный подмассивы.

Длина сортированной части равна 1 в начале и соответствует первому (левому) элементу в массиве. После этого остается итерировать массив и расширять отсортированную часть массива одним элементом с каждой новой итерацией.

После расширения новый элемент помещается на свое место в отсортированном подмассиве. Это происходит путём сдвига всех элементов вправо, пока не встретится элемент, который не нужно двигать.

В приведенном ниже массиве жирная часть отсортирована в порядке возрастания. Посмотрите что произойдет в этом случае:

• 3 5 7 8 4 2 1 9 6: выбираем 4 и помним, что это элемент, который нужно вставить. 8 > 4, поэтому сдвигаем.
• 3 5 7 x 8 2 1 9 6: здесь x – нерешающее значение, так как элемент будет перезаписан (на 4, если это подходящее место, или на 7, если смещение). 7 > 4, поэтому сдвигаемся.
• 3 5 x 7 8 2 1 9 6
• 3 x 5 7 8 2 1 9 6
• 3 4 5 7 8 2 1 9 6

Теперь вы видите, что отсортированная часть дополнилась элементом. Каждая следующая итерация делает то же самое, и к концу вы получите отсортированный массив!

Реализация

public static void insertionSort(int[] array) {  
    for (int i = 1; i < array.length; i++) {
        int current = array[i];
        int j = i - 1;
        while(j >= 0 && current < array[j]) {
            array[j+1] = array[j];
            j--;
        }
         // в этой точке мы вышли, так что j так же -1 
         // или в первом элементе, где текущий >= a[j]
        array[j+1] = current;
    }
}

Временная сложность

Вернемся к худшему сценарию – к массиву, отсортированному в убывающем порядке.

В этом случае каждая итерация сдвигает отсортированный массив на единицу O(n). Придется делать это для каждого элемента в каждом массиве, что приведет к сложности равной O(n ^ 2).

Сортировка выбором

Сортировка выбором тоже разделяет массив на сортированный и несортированный подмассивы. Но на этот раз сортированный подмассив формируется вставкой минимального элемента не отсортированного подмассива в конец сортированного, заменой:

• 3 5 1 2 4
• 1 5 3 2 4
• 1 2 3 5 4
• 1 2 3 5 4
• 1 2 3 4 5
• 1 2 3 4 5

Реализация

В каждой итерации вы предполагаете, что первый неотсортированный элемент минимален и итерируете по всем оставшимся элементам в поисках меньшего.

После нахождения текущего минимума неотсортированной части массива вы меняете его местами с первым элементом, и он уже часть отсортированного массива:

public static void selectionSort(int[] array) {  
    for (int i = 0; i < array.length; i++) {
        int min = array[i];
        int minId = i;
        for (int j = i+1; j < array.length; j++) {
            if (array[j] < min) {
                min = array[j];
                minId = j;
            }
        }
        // замена
        int temp = array[i];
        array[i] = min;
        array[minId] = temp;
    }
}

Временная сложность

При поиске минимума для длины массива проверяются все элементы, поэтому сложность равна O(n). Поиск минимума для каждого элемента массива равен O(n^2).

Сортировка слиянием

Сортировка слиянием эффективнее, чем примеры алгоритмов сортировки, представленные выше, благодаря использованию рекурсии и подходу «разделяй и властвуй».

Массив делится на два подмассива, а затем происходит:

1. Сортировка левой половины массива (рекурсивно)
2. Сортировка правой половины массива (рекурсивно)
3. Слияние

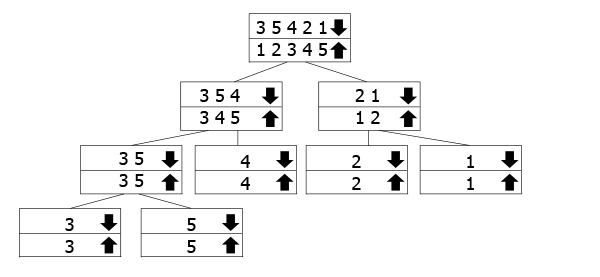
На схеме показана работа рекурсивных вызовов. Для массивов, отмеченных стрелкой вниз, вызывается функция. Во время слияния возвращаются массивы со стрелкой вверх. Всё просто: мы следуем за стрелкой вниз к нижней части дерева, а затем возвращаемся и объединяем.

В примере массив 3 5 4 2 1 делится на 3 5 4 и 2 1 и так далее. При достижении «дна» начинается объединение и сортировка.

Реализация

В главную функцию передаются left и right – индексы подмассивов для сортировки, крайние слева и справа. Изначально они имеют значения 0 и array.length-1, в зависимости от реализации.

Основа нашей рекурсии гарантирует, что мы выйдем, когда закончим, или когда left и right встретятся друг с другом. Мы находим среднюю точку mid и рекурсивно сортируем подмассивы слева и справа от середины, в итоге объединяя наши решения.

Возможно, вы вспомните дерево и спросите: почему мы не передаем два меньших массива? Ответ прост: это не нужно и вызовет огромное потребление памяти для очень длинных массивов.

Достаточно следовать индексам не нарушая логики дерева рекурсии:

public static void mergeSort(int[] array, int left, int right) {  
    if (right <= left) return;
    int mid = (left+right)/2;
    mergeSort(array, left, mid);
    mergeSort(array, mid+1, right);
    merge(array, left, mid, right);
}

Для сортировки двух подмассивов в один нужно вычислить их длину и создать временные массивы, в которые будем копировать. Так можно свободно изменять главный массив.

После копирования мы проходим по результирующему массиву и назначаем текущий минимум. Помните, что наши подмассивы отсортированы? Теперь нужно просто выбрать наименьший из двух элементов, которые еще не были выбраны, и двигать итератор для этого массива вперед:

 void merge(int[] array, int left, int mid, int right) {
    // вычисляем длину
    int lengthLeft = mid - left + 1;
    int lengthRight = right - mid;

    // создаем временные подмассивы
    int leftArray[] = new int [lengthLeft];
    int rightArray[] = new int [lengthRight];

    // копируем отсортированные массивы во временные
    for (int i = 0; i < lengthLeft; i++)
        leftArray[i] = array[left+i];
    for (int i = 0; i < lengthRight; i++)
        rightArray[i] = array[mid+i+1];

    // итераторы содержат текущий индекс временного подмассива
    int leftIndex = 0;
    int rightIndex = 0;

    // копируем из leftArray и rightArray обратно в массив  
    for (int i = left; i < right + 1; i++) {
        // если остаются нескопированные элементы в R и L, копируем минимальный
        if (leftIndex < lengthLeft && rightIndex < lengthRight) {
            if (leftArray[leftIndex] < rightArray[rightIndex]) {
                array[i] = leftArray[leftIndex];
                leftIndex++;
            }
            else {
                array[i] = rightArray[rightIndex];
                rightIndex++;
            }
        }
        // если все элементы были скопированы из rightArray, скопировать остальные из leftArray
        else if (leftIndex < lengthLeft) {
            array[i] = leftArray[leftIndex];
            leftIndex++;
        }
        // если все элементы были скопированы из leftArray, скопировать остальные из rightArray
        else if (rightIndex < lengthRight) {
            array[i] = rightArray[rightIndex];
            rightIndex++;
        }
    }
}

Временная сложность

Хотите легко рассчитывать рекурсивные реализации алгоритмов сортировки? Приготовьтесь к математике :)

Для вычисления временной сложности нам понадобится основная теорема о рекуррентных соотношениях. Временную сложность рекурсивных алгоритмов сортировки можно описать следующим уравнением:

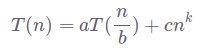
Здесь a – это количество меньших рекурсивных вызовов, на которые мы делим проблему, а b указывает на входную величину рекурсивных вызовов.

Остальная часть уравнения – это сложность слияния всех решений в одно конечное. Упомянутая теорема решит все за вас:

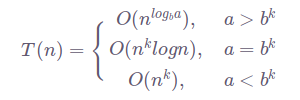
Если T(n) – это время выполнения алгоритма для сортировки массива длинной n, сортировка слиянием запустится дважды для массивов длиной вполовину от оригинального.

Так, если a=2, b=2, шаг слияния занимает O(n) памяти при k=1. Это означает, что уравнение для сортировки слиянием будет выглядеть так:

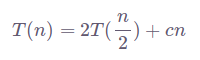
Примените теорему, и вы увидите, что в нашем случае a=b^k, ибо 2=2^1. Значит, сложность равна O(nlog n), и это лучшая временная сложность для алгоритма сортировки. Доказано, что массив не может быть отсортирован быстрее, чем O(nlog n).

Пирамидальная сортировка

Для понимания работы пирамидального алгоритма сортировки нужно понять структуру, на которой он основан – пирамиду.

Пирамида или двоичная куча – это дерево, в котором каждый узел состоит в отношениях с дочерними узлами. Добавление нового узла начинается с левой позиции нижнего неполного уровня.

По мере движения вниз по дереву значения уменьшаются (min-heap) или увеличиваются (max-heap). Смотрите пример max-heap:

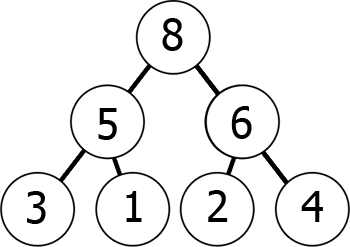
А теперь представим пирамиду в виде массива:

8 5 6 3 1 2 4

Чтение графа сверху вниз здесь представлено слева направо. Мы добились того, что позиция дочернего элемента по отношению к k-ому элементу в массиве – 2\*k+1 и 2\*k+2 (при условии, что индексация начинается с 0). Проверьте сами!

И наоборот, для k-го элемента дочерняя позиция всегда равна (k-1)/2.

С этими знаниями вы сделаете max-heap из любого массива! Для этого проверьте каждый элемент на условие, что каждый из его дочерних элементов имеет меньшее значение.

Условие верно? Тогда меняйте местами один из дочерних элементов с родительским и повторяйте рекурсию с новым родительским элементом (он может всё ещё быть больше другого дочернего).

• 6 1 8 3 5 2 4: оба дочерних меньше родительского, оставляем как есть.
• 6 1 8 3 5 2 4: 5 > 1, поэтому меняем их. Теперь рекурсивно проверяем 5.
• 6 5 8 3 1 2 4: оба дочерних меньше 5, поэтому пропускаем.
• 6 5 8 3 1 2 4: 8 > 6, поэтому меняем их.
• 8 5 6 3 1 2 4: мы получили пирамиду, изображенную выше!

Вы научились строить пирамиду из массива, все остальное гораздо проще! Поменяйте местами корень пирамиды с концом массива, и сократите массив на единицу.

Постройте кучу из сокращенного массива и повторяйте процесс:

• 8 5 6 3 1 2 4
• 4 5 6 3 1 2 8: замена
• 6 5 4 3 1 2 8: сортировка
• 2 5 4 3 1 6 8: замена
• 5 2 4 2 1 6 8: сортировка
• 1 2 4 2 5 6 8: замена

И так далее. Видите закономерность?

Реализация

static void heapify(int[] array, int length, int i) {  
    int leftChild = 2*i+1;
    int rightChild = 2*i+2;
    int largest = i;

    // если левый дочерний больше родительского
    if (leftChild < length && array[leftChild] > array[largest]) {
        largest = leftChild;
    }

    // если правый дочерний больше родительского
    if (rightChild < length && array[rightChild] > array[largest]) {
        largest = rightChild;
    }

    // если должна произойти замена
    if (largest != i) {
        int temp = array[i];
        array[i] = array[largest];
        array[largest] = temp;
        heapify(array, length, largest);
    }
}

public static void heapSort(int[] array) {  
    if (array.length == 0) return;

    // Строим кучу
    int length = array.length;
    // проходим от первого без ответвлений к корню
    for (int i = length / 2-1; i >= 0; i--)
        heapify(array, length, i);

    for (int i = length-1; i >= 0; i--) {
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;

        heapify(array, i, 0);
    }
}

Временная сложность

Посмотрите на функцию heapify() – кажется, что все делается за O(1), верно? Но нет же: все портит рекурсивный вызов!

Готовы посчитать, сколько вызовов нужно в наихудшем сценарии? В худшем случае рекурсивный вызов дойдет до самой вершины пирамиды прыжками к родителям каждого узла в отношении i/2. Всего потребуется log n прыжков до вершины, значит, сложность равна O(log n).

Это ещё не всё!

В связи с циклами for, которые итерируют весь массив, сложность heapSort() равна O(n). Это дает нам суммарную сложность пирамидальной сортировки O(nlog n).

Быстрая сортировка

На этом участнике нашего топа мы закончим разбирать примеры алгоритмов сортировки.

Перед вами очередной алгоритм техники «разделяй и властвуй». Он выбирает один элемент массива в качестве стержня и сортирует остальные элементы вокруг (меньшие элементы налево, большие направо).

Так соблюдается правильная позиция самого «стержня». Затем алгоритм рекурсивно повторяет сортировку для правой и левой частей.

Реализация

static int partition(int[] array, int begin, int end) {  
    int pivot = end;

    int counter = begin;
    for (int i = begin; i < end; i++) {
        if (array[i] < array[pivot]) {
            int temp = array[counter];
            array[counter] = array[i];
            array[i] = temp;
            counter++;
        }
    }
    int temp = array[pivot];
    array[pivot] = array[counter];
    array[counter] = temp;

    return counter;
}

public static void quickSort(int[] array, int begin, int end) {  
    if (end <= begin) return;
    int pivot = partition(array, begin, end);
    quickSort(array, begin, pivot-1);
    quickSort(array, pivot+1, end);
}

Временная сложность

Временную сложность алгоритма быстрой сортировки можно описать следующим уравнением:

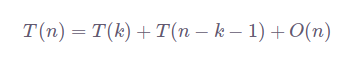
В наихудшем сценарии наибольший и наименьший элементы всегда выбираются в качестве стержня. Тогда уравнение приобретает вид:

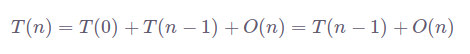
Получается O(n^2).

На фоне алгоритмов сортировки со сложностью O(nlog n), выглядит не очень :(

На практике быстрая сортировка применяется широко. Судите сами: у алгоритма очень хорошее среднее время запуска, также равное O(nlog n), он эффективен для больших потоков ввода. И на этом преимущества не заканчиваются!

Алгоритм не занимает дополнительного пространства, вся сортировка происходит «на месте», отсутствуют затратные вызовы распределения, из-за чего его часто предпочитают сортировке слиянием.

На этом всё! Не пропустите книги по Java, среди которых Алгоритмы на Java – Роберт Седжвик, Кевин Уэйн – полезная книга для дальнейшего погружения в тему.

Источник

Понятны принципы алгоритмов сортировки? Продолжайте покорять язык программирования Java:

• 6 алгоритмов поиска на Java: от простого к сложному
• Java 12 и всё, что должен знать Java-программист