🍺📊 Какая связь между пивом и t-распределением? Рассказывает Кирилл Дубовиков из компании «Синимекс»

Автор: Кирилл Дубовиков, Директор по анализу данных и машинному обучению компании «Синимекс».

Нормальное распределение

Представим, что нам нужно исследовать рост людей в городе. Мы выходим на улицу и начинаем измерять рост случайных прохожих. (Некоторые из них могут вызвать полицию, но это же все ради науки!)

Нам нужно провести немного разведочного анализа данных как порядочным data scientist’ам. Но под рукой нет статистических инструментов, таких как язык R, поэтому мы просто берем и строим гистограмму из людей.

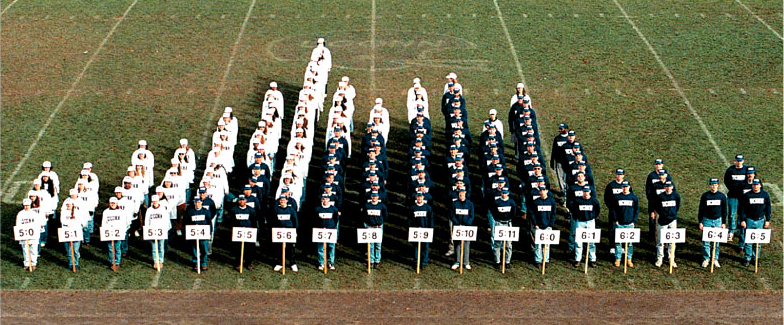
Мы видим самое важное распределение вероятности, с которым когда-либо нужно будет иметь дело — распределение Гаусса. Благодаря центральной предельной теореме, его можно обнаружить во множестве реальных процессов нашего мира. Распределение Гаусса встречается настолько часто, что его также называют нормальным распределением.

Центральная предельная теорема гласит, что среднее арифметическое достаточно большого числа случайных переменных величин имеет нормальное распределение. Сами эти величины могут изначально иметь любое распределение, но их сумма (по мере приближения количества этих величин к ∞) будет иметь вид нормального распределения.

Функция плотности распределения Гаусса представлена ниже:

Эта формула выглядит пугающе, но математически с ней удобно работать. Если вам интересно, как она выводится, можете почитать об этом здесь. Как видно, у этого распределения есть два параметра:

• µ (математическое ожидание)
• σ (стандартное отклонение).

Математическое ожидание µ определяет математическое ожидание случайной величины с нормальным распределением. Дисперсия σ² определяет меру разброса возможных значений.

Из-за вездесущего присутствия в реальных данных нормальное распределение часто используется в машинном обучении. Оно широко используется в различных алгоритмах, к примеру:

• Подразумевается, что ошибки в линейных моделях имеют нормальное распределение.
• Гауссовские процессы предполагают, что значения функции в рамках модели имеют нормальное распределение.
• Смешанные гауссовские модели позволяют моделировать сложные распределения, используя несколько «простых» нормальных распределений.
• Нормальное распределение является одним из основных компонентов в вариационных автокодировщиках.

По ссылке представлено интерактивное демо Гауссова распределения:

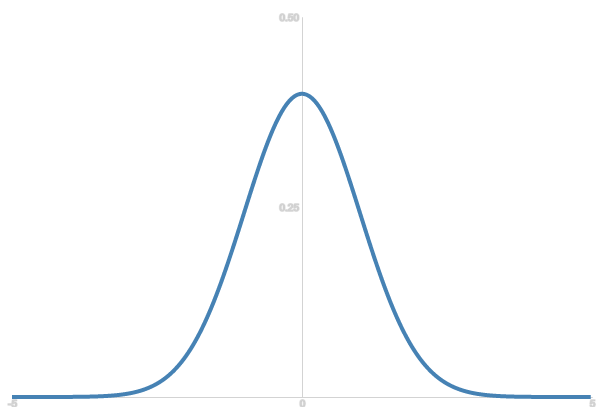
t-распределение Стьюдента

Что если бы мы захотели моделировать данные по Гауссову распределению, но истинная величина дисперсии σ² была бы нам не известна? Такая проблема возникает, когда выборка маленькая и стандартное отклонение (σ) невозможно оценить с достаточной точностью.

Уильям Госсет столкнулся с этой проблемой, оценивая качество пива Guinness. Он эмпирическим образом вывел формулу для случайной переменной, имеющей t-распределение.

Для начала, допустим у нас есть ряд значений x, …, xn, которые были получены путем выборки из нормального распределения N(µ, σ²).

Мы не знаем величину истинной дисперсии, но мы можем примерно оценить ее, рассчитав выборочное среднее и дисперсию:

Тогда случайная переменная

будет иметь t-распределение с числом степеней свободы n-1 , где n это число элементов в выборке.

Эта формула похожа на трансформацию нормального распределения в стандартное нормальное (это условное название нормального распределения, где математическое ожидание равно 0, а дисперсия – 1):

Мы не знаем, чему равна истинная дисперсия для всей генеральной совокупности, поэтому мы вынуждены заменить ее на выборочное стандартное отклонение.

Это распределение лежит в основе научного метода, который называется t-тест. Он был впервые использован в компании Guinness для оценки качества их пива.

Уильям Госсет опубликовал результаты своего исследования под псевдонимом Стьюдент, так как в Guinness волновались о том, что конкуренты узнают о методике использования t-теста для контроля качества своей продукции.

Метод, обнаруженный Госсетом, впоследствии был доработан знаменитым статистиком Рональдом Фишером. Фишер считается родоначальником частотного подхода к статистике.

Пощупать t-распределение в интерактивном режиме можно по ссылке.

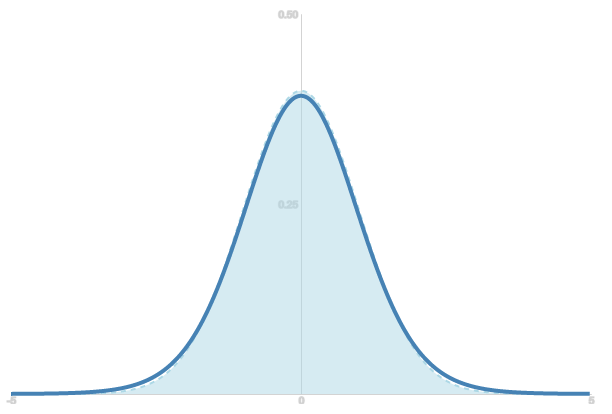
Как вы можете видеть, t-распределение приближается к нормальному на больших числах степеней свободы. Это происходит, потому что выборочное среднее приближается к истинному среднему по мере того, как размер выборки приближается к бесконечности. А «толстые» хвосты t-распределения компенсируют состояние неопределенности при работе с выборкой малого размера.

Логично задать вопрос: «Чему равна плотность распределения вероятностей t-распределения? Как мы можем вывести её?» Это непростая задача с точки зрения математики, но в основе её лежит достаточно понятная мысль.

Предположим, что мы хотим узнать плотность распределения вероятностей нормальной переменной X ~ N(0, σ). Но без прямой зависимости от стандартного отклонения σ.

Для того, чтобы избавиться от σ, нам нужно будет сделать ряд предположений. Давайте считать саму σ случайной переменной, и предположим, что она следует Гамма-распределению. Гамма-распределение позволяет описать одной формулой целое семейство различных распределений, из-за чего оказывается удобным инструментом в таких случаях.

Таким образом, X представляет собой смесь двух непрерывных вероятностных распределений – нормального и Гамма. После этого мы исключаем путем интегрирования σ и получаем формулу плотности распределения вероятности для t-распределения.

Заключение

Распределения Гаусса и Стьюдента относятся к важнейшим непрерывным вероятностным распределениям в статистике и машинном обучении.

T-распределение может использоваться взамен Гауссова в случае, когда дисперсия генеральной совокупности не известна, или для выборок малых размеров. Оба эти распределения тесно связаны между собой.

Спасибо, что прочитали эту статью. Надеюсь, вы открыли для себя что-то новое или освежили свои знания.