В этом руководстве мы научимся применять простейшие трансформации изображений в приложениях на языке C#. Для этого реализуем в коде базовые концепции линейной алгебры: умножение матриц, скалярное произведение векторов и применение матриц трансформации к пикселям. Дочитав статью, вы будете знать, как повернуть, растянуть, отразить и перекрасить картинку прямо из кода на C#.
Умножение матриц
Матричное умножение – довольно незамысловатая операция. Реализуем функцию умножения матриц в коде. Если вам не хватает знаний линейной алгебры, наглядное представление можно получить из нашей публикации. Для начала создадим C#-класс Matrices и его основной метод Multiply:
public static double[,] Multiply(double[,] matrix1, double[,] matrix2) {
// кэшируем размеры матриц для лучшей производительности
var matrix1Rows = matrix1.GetLength(0);
var matrix1Cols = matrix1.GetLength(1);
var matrix2Rows = matrix2.GetLength(0);
var matrix2Cols = matrix2.GetLength(1);
// проверяем, совместимы ли матрицы
if (matrix1Cols != matrix2Rows)
throw new InvalidOperationException
("Матрицы не совместимы. Число столбцов первой матрицы должно быть равно числу строк второй матрицы");
// создаем пустую результирующую матрицу нужного размера
double[,] product = new double[matrix1Rows, matrix2Cols];
// заполняем результирующую матрицу
// цикл по каждому ряду первой матрицы
for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) {
// цикл по каждому столбцу второй матрицы
for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) {
// вычисляем скалярное произведение двух векторов
for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) {
product[matrix1_row, matrix2_col] +=
matrix1[matrix1_row, matrix1_col] *
matrix2[matrix1_col, matrix2_col];
}
}
}
return product;
}
Мы начинаем с определения размеров обеих матриц с помощью метода Array.GetLength(). Записываем полученные результаты в переменные, чтобы не пришлось их заново вычислять. Далее убеждаемся, что полученные матрицы в принципе можно перемножить: число столбцов первой матрицы должно равняться количеству строк второй, иначе выбрасываем исключение.
На следующем шаге создаем заготовку выходной матрицы нужного размера. Наконец, нужно заполнить каждую ячейку матрицы-произведения. Для этого последовательно умножаем каждый ряд первой матрицы на каждый столбец второй. По сути, каждый ряд и каждая колонка – это вектор, скалярное произведение которых дает нам соответствующий элемент итоговой матрицы.
Трансформации
Теперь можно использовать алгоритм умножения для того, чтобы создать матрицу трансформации изображения. Эту матрицу затем нужно последовательно применить к каждой точке изображения (X, Y) или к ее цвету (ARGB). В результате мы получим новое – трансформированное – изображение.
Начнем с определения абстрактного интерфейса трансформации IImageTransformation с двумя членами: методом CreateTransformationMatrix() и булевым свойством IsColorTransformation.
public interface IImageTransformation {
double[,] CreateTransformationMatrix();
bool IsColorTransformation { get; }
}
Теперь разберемся, что нужно сделать с пикселями исходного изображения, чтобы применить к нему ту или иную трансформацию.
Вращение
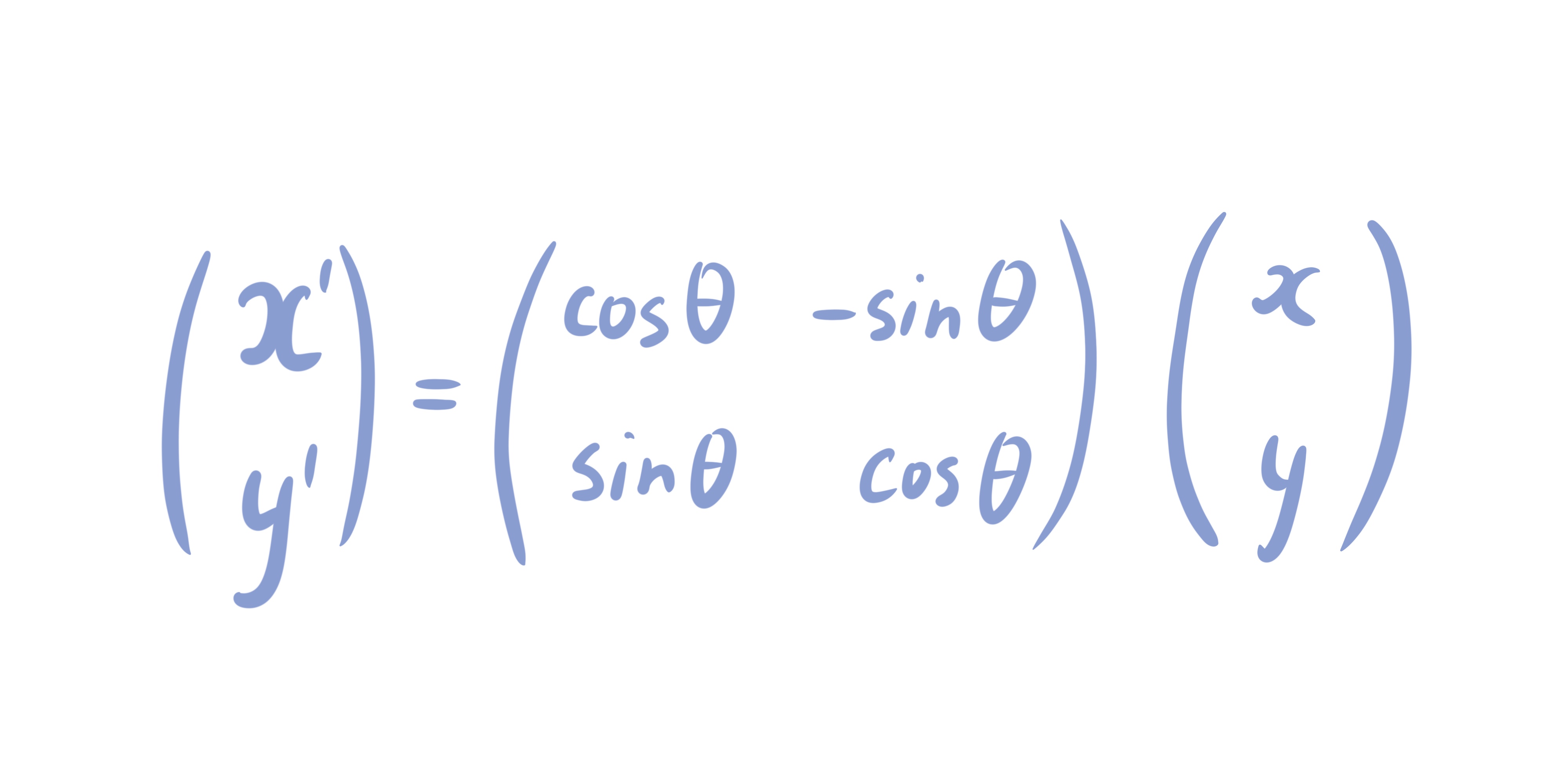
На основе приведенной выше матрицы поворота напишем класс, отвечающий за вращение:
public class RotationImageTransformation : IImageTransformation {
public double AngleDegrees { get; set; }
public double AngleRadians {
get { return DegreesToRadians(AngleDegrees); }
set { AngleDegrees = RadiansToDegrees(value); }
}
public bool IsColorTransformation { get { return false; } }
public static double DegreesToRadians(double degree)
{ return degree * Math.PI / 180; }
public static double RadiansToDegrees(double radians)
{ return radians / Math.PI * 180; }
public double[,] CreateTransformationMatrix() {
double[,] matrix = new double[2, 2];
matrix[0, 0] = Math.Cos(AngleRadians);
matrix[1, 0] = Math.Sin(AngleRadians);
matrix[0, 1] = -1 * Math.Sin(AngleRadians);
matrix[1, 1] = Math.Cos(AngleRadians);
return matrix;
}
public RotationImageTransformation() { }
public RotationImageTransformation(double angleDegree) {
this.AngleDegrees = angleDegree;
}
}
Функции Sin() и Cos() принимают углы в радианах, поэтому мы добавили две дополнительные функции для конвертации градусов в радианы и обратно, чтобы упростить взаимодействие для конечного пользователя класса.
Объяснение матрицы вращения вокруг точки доступно изложено в статье 2D Rotation about a point.
Растягивание/Масштабирование
Вторая популярная трансформация – масштабирование по определенному коэффициенту. Она работает путем простого умножения нужных координат (X/Y) на коэффициент масштабирования по соответствующей оси (xk, ytk). Напишем класс для этой трансформации в 2D-пространстве:
public class StretchImageTransformation : IImageTransformation {
public double HorizontalStretch { get; set; }
public double VerticalStretch { get; set; }
public bool IsColorTransformation { get { return false; } }
public double[,] CreateTransformationMatrix() {
// создаем единичную матрицу 2х2
double[,] matrix = Matrices.CreateIdentityMatrix(2);
matrix[0, 0] += HorizontalStretch;
matrix[1, 1] += VerticalStretch;
return matrix;
}
public StretchImageTransformation() { }
public StretchImageTransformation(double horizStretch, double vertStretch) {
this.HorizontalStretch = horizStretch;
this.VerticalStretch = vertStretch;
}
}
Единичная матрица
Следующий код использует единичную матрицу – такую, у которой по диагонали единицы, а остальные элементы нулевые. Она не приводит ни к каким изменениям исходного изображения и нужна лишь в качестве основы для удобного построения матрицы трансформации.
public static double[,] CreateIdentityMatrix(int length) {
double[,] matrix = new double[length, length];
for (int i = 0, j = 0; i < length; i++, j++)
matrix[i, j] = 1;
return matrix;
}
Добавьте этот метод в класс Matrices.
Отражение
Третья трансформация, с которой мы будем работать – отражение. Она выполняется за счет изменения знака X и Y – соответственно вектор переворачивается по вертикальной или горизонтальной оси. Класс для применения этой матрицы выглядит так:
public class FlipImageTransformation : IImageTransformation {
public bool FlipHorizontally { get; set; }
public bool FlipVertically { get; set; }
public bool IsColorTransformation { get { return false; } }
public double[,] CreateTransformationMatrix() {
// создаем единичную матрицу 2х2
double[,] matrix = Matrices.CreateIdentityMatrix(2);
if (FlipHorizontally)
matrix[0, 0] *= -1;
if (FlipVertically)
matrix[1, 1] *= -1;
return matrix;
}
public FlipImageTransformation() { }
public FlipImageTransformation(bool flipHoriz, bool flipVert) {
this.FlipHorizontally = flipHoriz;
this.FlipVertically = flipVert;
}
}
Преобразование цвета
Последняя трансформация, которую мы рассмотрим, – изменение цветовой плотности. Она предусматривает применение разных коэффициентов к компонентам цвета (красный, зеленый, синий и альфа-канал). Например, если требуется сделать изображение на 50% прозрачным, нужно умножить значение альфа-канала на 0.5. Чтобы удалить полностью красный цвет, нужно умножить его на 0, и так далее.
public class DensityImageTransformation : IImageTransformation {
public double AlphaDensity { get; set; }
public double RedDensity { get; set; }
public double GreenDensity { get; set; }
public double BlueDensity { get; set; }
public bool IsColorTransformation { get { return true; } }
public double[,] CreateTransformationMatrix() {
// identity matrix
double[,] matrix = new double[,]{
{ AlphaDensity, 0, 0, 0},
{ 0, RedDensity, 0, 0},
{ 0, 0, GreenDensity, 0},
{ 0, 0, 0, BlueDensity},
};
return matrix;
}
public DensityImageTransformation() { }
public DensityImageTransformation(double alphaDensity,
double redDensity,
double greenDensity,
double blueDensity) {
this.AlphaDensity = alphaDensity;
this.RedDensity = redDensity;
this.GreenDensity = greenDensity;
this.BlueDensity = blueDensity;
}
}
Собираем всё вместе
Теперь нужно лишь собрать из отдельных трансформаций целый инструмент. Создадим класс ImageTransformer, отвечающий за преобразование изображения и добаим в него следующие методы:
struct PointColor
{
public int X { get; set; }
public int Y { get; set; }
public Color Color { get; set; }
public PointColor(int X, int Y, Color Color)
{
this.X = X;
this.Y = Y;
this.Color = Color;
}
}
///
/// Применяет трансформации к файлу изображения
///
public static Bitmap Apply(string file, IImageTransformation[] transformations) {
using (Bitmap bmp = (Bitmap)Bitmap.FromFile(file)) {
return Apply(bmp, transformations);
}
}
///
/// Применяет трансформации к bitmap-объекту
///
public static Bitmap Apply(Bitmap bmp, IImageTransformation[] transformations) {
// определение массива для хранения данных нового изображения
PointColor[] points = new PointColor[bmp.Width * bmp.Height];
// разделение преобразований на пространственные и цветовые
var pointTransformations =
transformations.Where(s => s.IsColorTransformation == false).ToArray();
var colorTransformations =
transformations.Where(s => s.IsColorTransformation == true).ToArray();
// создание матриц трансформации
double[,] pointTransMatrix =
CreateTransformationMatrix(pointTransformations, 2); // x, y
double[,] colorTransMatrix =
CreateTransformationMatrix(colorTransformations, 4); // a, r, g, b
// сохранение координат для последующей настройки
int minX = 0, minY = 0;
int maxX = 0, maxY = 0;
// перебор точек и применение трансформаций
int idx = 0;
for (int x = 0; x < bmp.Width; x++) { // ряд за рядом
for (int y = 0; y < bmp.Height; y++) { // колонка за колонкой
// применение пространственных трансформаций
var product =
Matrices.Multiply(pointTransMatrix, new double[,] { { x }, { y } });
var newX = (int)product[0, 0];
var newY = (int)product[1, 0];
// обновление координат
minX = Math.Min(minX, newX);
minY = Math.Min(minY, newY);
maxX = Math.Max(maxX, newX);
maxY = Math.Max(maxY, newY);
// применение трансформаций цвета
Color clr = bmp.GetPixel(x, y); // текущий цвет
var colorProduct = Matrices.Multiply(
colorTransMatrix,
new double[,] { { clr.A }, { clr.R }, { clr.G }, { clr.B } });
clr = Color.FromArgb(
GetValidColorComponent(colorProduct[0, 0]),
GetValidColorComponent(colorProduct[1, 0]),
GetValidColorComponent(colorProduct[2, 0]),
GetValidColorComponent(colorProduct[3, 0])
); // новый цвет
// сохранение новых данных пикселя
points[idx] = new PointColor() {
X = newX,
Y = newY,
Color = clr
};
idx++;
}
}
// ширина и высота растра после трансформаций
var width = maxX - minX + 1;
var height = maxY - minY + 1;
// новое изображение
var img = new Bitmap(width, height);
foreach (var pnt in points)
img.SetPixel(
pnt.X - minX,
pnt.Y - minY,
pnt.Color);
return img;
}
///
/// Возвращает цвет от 0 до 255
///
private static byte GetValidColorComponent(double c) {
c = Math.Max(byte.MinValue, c);
c = Math.Min(byte.MaxValue, c);
return (byte)c;
}
///
/// Объединяет преобразования в единую матрицу трансформации
///
private static double[,] CreateTransformationMatrix
(IImageTransformation[] vectorTransformations, int dimensions) {
double[,] vectorTransMatrix =
Matrices.CreateIdentityMatrix(dimensions);
// перемножает матрицы трансформации
foreach (var trans in vectorTransformations)
vectorTransMatrix =
Matrices.Multiply(vectorTransMatrix, trans.CreateTransformationMatrix());
return vectorTransMatrix;
}
Мы начали с определения двух перегрузок функции Apply. Одна из них принимает первым параметром имя файла изображения, а другая – bitmap-объект. вторым аргументом передается список трансформаций, которые нужно применить.
Внутри Apply() преобразования разделяются на 2 группы:
- манипулирующие положением точек (
XиY); - манипулирующие цветом.
Для каждой группы объединяем трансформации в единую матрицу с помощью функции CreateTransformationMatrix().
Затем сканируем изображение и применяем преобразования к точкам и цветам соответственно. Обратите внимание, мы добавили проверку на то, что преобразованные значения каналов находятся в допустимом диапазоне.
После применения трансформаций данные сохраняются в массиве для последующего использования.
В процессе сканирования мы отслеживаем минимальные и максимальные координаты. Это нужно, чтобы установить новый размер изображения, который может отличаться от исходного после применения изменений.
Наконец, создаем bitmap-объект с новыми данными изображения.
Создание клиента
Клиентская часть приложения очень простая. Вот так выглядит форма для ввода данных:
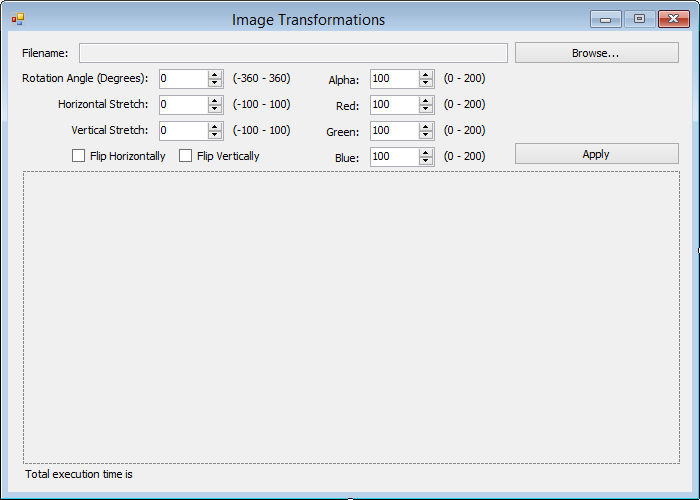
Взглянем на управляющий ей код:
private string _file;
private Stopwatch _stopwatch;
public ImageTransformationsForm() {
InitializeComponent();
}
private void BrowseButton_Click(object sender, EventArgs e) {
string file = OpenFile();
if (file != null) {
this.FileTextBox.Text = file;
_file = file;
}
}
public static string OpenFile() {
OpenFileDialog dlg = new OpenFileDialog();
dlg.CheckFileExists = true;
if (dlg.ShowDialog() == DialogResult.OK)
return dlg.FileName;
return null;
}
private void ApplyButton_Click(object sender, EventArgs e) {
if (_file == null)
return;
DisposePreviousImage();
RotationImageTransformation rotation =
new RotationImageTransformation((double)this.AngleNumericUpDown.Value);
StretchImageTransformation stretch =
new StretchImageTransformation(
(double)this.HorizStretchNumericUpDown.Value / 100,
(double)this.VertStretchNumericUpDown.Value / 100);
FlipImageTransformation flip =
new FlipImageTransformation(this.FlipHorizontalCheckBox.Checked, this.FlipVerticalCheckBox.Checked);
DensityImageTransformation density =
new DensityImageTransformation(
(double)this.AlphaNumericUpDown.Value / 100,
(double)this.RedNumericUpDown.Value / 100,
(double)this.GreenNumericUpDown.Value / 100,
(double)this.BlueNumericUpDown.Value / 100
);
StartStopwatch();
var bmp = ImageTransformer.Apply(_file,
new IImageTransformation[] { rotation, stretch, flip, density });
StopStopwatch();
this.ImagePictureBox.Image = bmp;
}
private void StartStopwatch() {
if (_stopwatch == null)
_stopwatch = new Stopwatch();
else
_stopwatch.Reset();
_stopwatch.Start();
}
private void StopStopwatch() {
_stopwatch.Stop();
this.ExecutionTimeLabel.Text = $"Total execution time is {_stopwatch.ElapsedMilliseconds} milliseconds";
}
private void DisposePreviousImage() {
if (this.ImagePictureBox.Image != null) {
var tmpImg = this.ImagePictureBox.Image;
this.ImagePictureBox.Image = null;
tmpImg.Dispose();
}
}
Единственное, что следует отметить, – это хорошая практика вызова Dispose() на disposable-объектах для лучшей производительности.
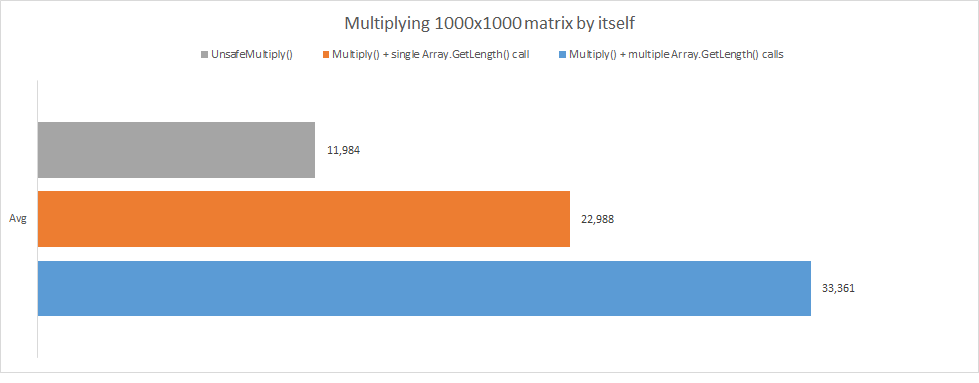
Анализ производительности
В основном методе Multiply() вызов метода Array.GetLength() оказывает большое влияние на производительность. В этом можно убедиться, сравнив скорость выполнения кода с многократным вызовом GetLength и с кэшированием результатов единственного вызова – они отличаются почти в 2 раза!
Еще один способ повысить производительность Multiply() – использовать небезопасный код, получив прямой доступ к содержимому массива:
public static double[,] MultiplyUnsafe(double[,] matrix1, double[,] matrix2) {
// кэшируем размеры матриц для лучшей производительности
var matrix1Rows = matrix1.GetLength(0);
var matrix1Cols = matrix1.GetLength(1);
var matrix2Rows = matrix2.GetLength(0);
var matrix2Cols = matrix2.GetLength(1);
// проверяем, совместимы ли матрицы
if (matrix1Cols != matrix2Rows)
throw new InvalidOperationException
("Матрицы не совместимы. Число столбцов первой матрицы должно быть равно числу строк второй матрицы");
// создаем пустую результирующую матрицу нужного размера
double[,] product = new double[matrix1Rows, matrix2Cols];
unsafe
{
// закрепляем указатели на матрицы
fixed (
double* pProduct = product,
pMatrix1 = matrix1,
pMatrix2 = matrix2) {
int i = 0;
// цикл по каждому ряду первой матрицы
for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) {
// цикл по каждому столбцу второй матрицы
for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) {
/// вычисляем скалярное произведение двух векторов
for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) {
var val1 = *(pMatrix1 + (matrix1Rows * matrix1_row) + matrix1_col);
var val2 = *(pMatrix2 + (matrix2Cols * matrix1_col) + matrix2_col);
*(pProduct + i) += val1 * val2;
}
i++;
}
}
}
}
return product;
}
Небезопасный код не будет компилироваться, если вы не разрешите эту опцию в меню Проект -> Свойства -> Сборка.
Теперь вы можете запустить приложение и убедиться, что все операции трансформаций работают. Готовый код проекта можно найти в этом репозитории.



Комментарии