🤖 Метод k-ближайших соседей (k-nearest neighbour)

• В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны.
• В случае использования метода для регрессии, объекту присваивается среднее значение по k ближайшим к нему объектам, значения которых уже известны.
  

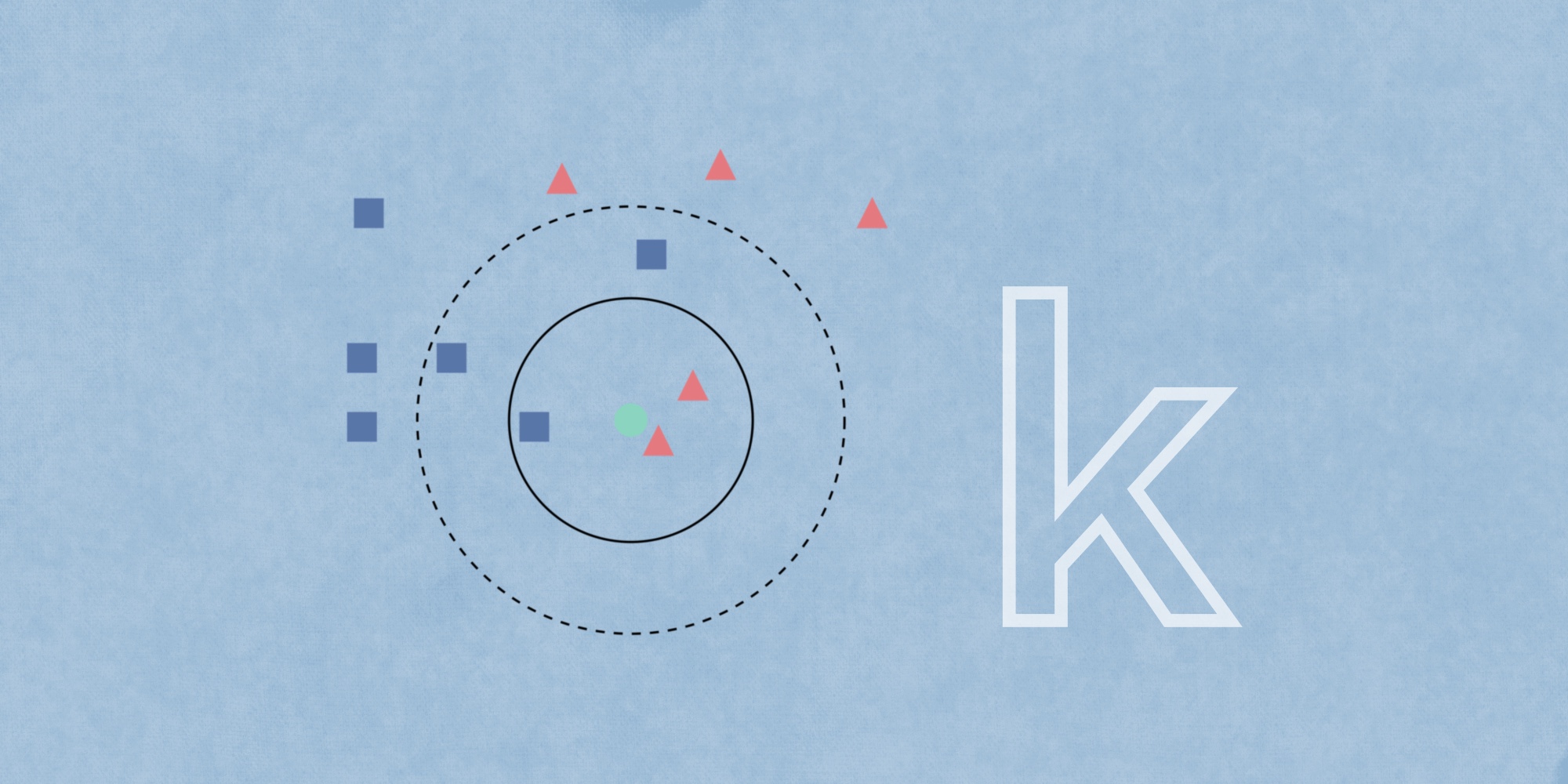
Пример классификации k-ближайших соседей.

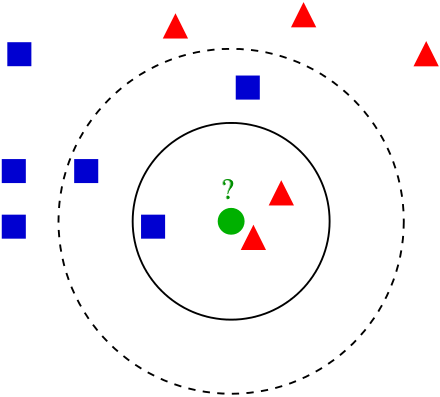
• У нас есть тестовый образец в виде зеленого круга. Синие квадраты мы обозначим как класс 1, красные треугольники – класс 2.
• Зеленый круг должен быть классифицирован как класс 1 или класс 2. Если рассматриваемая нами область является малым кругом, то объект классифицируется как 2-й класс, потому что внутри данного круга 2 треугольника и только 1 квадрат.
  
• Если мы рассматриваем большой круг (с пунктиром), то круг будет классифицирован как 1-й класс, так как внутри круга 3 квадрата в противовес 2 треугольникам.
  

Теоретическая составляющая алгоритма k-NN

Помимо простого объяснения, необходимо понимание основных математических составляющих алгоритма k-ближайших соседей.

• Евклидова метрика (евклидово расстояние, или же Euclidean distance) – метрика в евклидовом пространстве, расстояние между двумя точками евклидова пространства, вычисляемое по теореме Пифагора. Проще говоря, это наименьшее возможное расстояние между точками A и B. Хотя евклидово расстояние полезно для малых измерений, оно не работает для больших измерений и для категориальных переменных. Недостатком евклидова расстояния является то, что оно игнорирует сходство между атрибутами. Каждый из них рассматривается как полностью отличный от всех остальных.

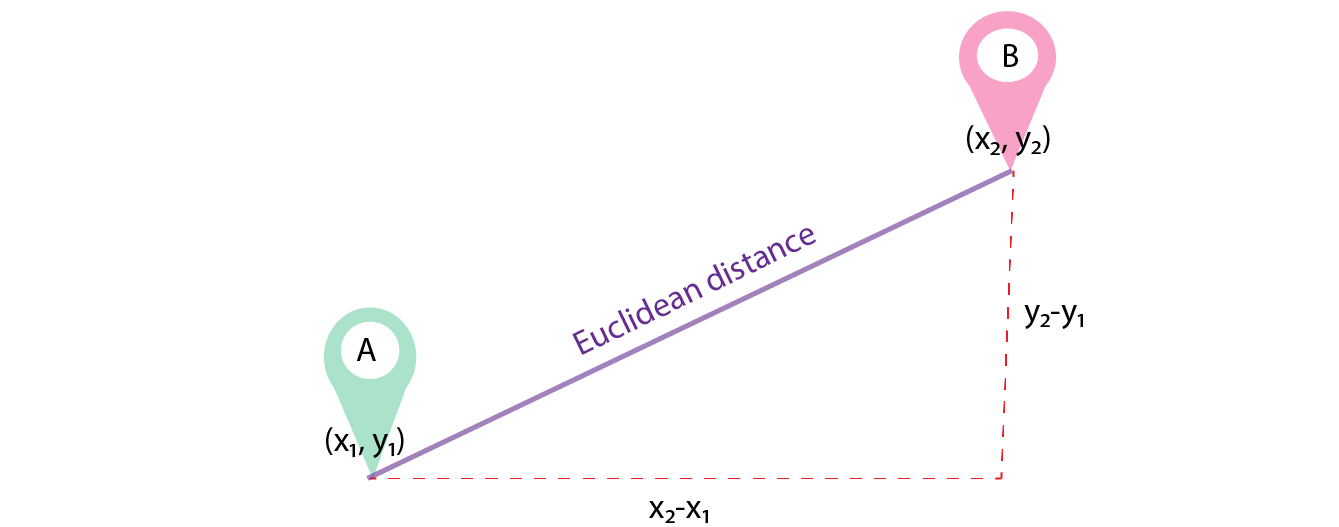
Формула вычисления Евклидова расстояния:

• Другой важной составляющей метода является нормализация. Разные атрибуты обычно обладают разным диапазоном представленных значений в выборке. К примеру, атрибут А представлен в диапазоне от 0.01 до 0.05, а атрибут Б представлен в диапазоне от 500 до 1000). В таком случае значения дистанции могут сильно зависеть от атрибутов с бо́льшими диапазонами. Поэтому данные в большинстве случаев проходят через нормализацию. При кластерном анализе есть два основных способа нормализации данных: MinMax-нормализация и Z-нормализация.

MinMax-нормализация осуществляется следующим образом:

в данном случае все значения будут находиться в диапазоне от 0 до 1; дискретные бинарные значения определяются как 0 и 1.

Z-нормализация:

где σ – среднеквадратичное отклонение. В данном случае большинство значений попадает в диапазон.

Каков порядок действий?

• Загрузите ваши данные.
  
• Инициализируйте k путем выбора оптимального числа соседей.
  
• Для каждого образца в данных:
  

1. Вычислите расстояние между примером запроса и текущим примером из данных.
   
2. Добавьте индекс образца в упорядоченную коллекцию, как и его расстояние.
   

• Отсортируйте упорядоченную коллекцию расстояний и индексов от наименьшего до наибольшего, в порядке возрастания.
• Выберите первые k записей из отсортированной коллекции.
  
• Возьмите метки выбранных k записей.
  
• Если у вас задача регрессии, верните среднее значение выбранных ранее k меток.
  
• Если у вас задача классификации, верните наиболее часто встречающееся значение выбранных ранее меток k.
  

Реализация на языке Python

Набор данных состоит из 15 столбцов, таких как sex (пол), fare (плата за проезд), p_class (класс каюты), family_size (размер семьи), и т. д. Главным признаком, который мы и должны предсказать в соревновании, является survived (выжил пассажир или нет).

Дополнительный анализ показал, что находящиеся в браке люди имеют больший шанс на то, чтобы быть спасенными с корабля. Поэтому были добавлены еще 4 столбца, переименованные из Name (Имя), которые обозначают мужчин и женщин в зависимости от того, были они женаты или нет (Mr, Mrs, Mister, Miss).

Чтобы наглядно продемонстрировать функциональность k-NN для предсказания выживания пассажира, мы рассматриваем только два признака: age (возраст), fare (плата за проезд).

        # Загружаем данные
train_df = pd.read_csv('/kaggle/input/titanic/train_data.csv') 
# Избавляемся от двух столбцов без нужной информации
train_df = train_df.drop(columns=['Unnamed: 0', 'PassengerId']) 
from sklearn.neighbors import KNeighborsClassifier 
predictors = ['Age', 'Fare'] 
outcome = 'Survived' 

new_record = train_df.loc[0:0, predictors] 
X = train_df.loc[1:, predictors] 
y = train_df.loc[1:, outcome] 

kNN = KNeighborsClassifier(n_neighbors=20) 
kNN.fit(X, y) 
kNN.predict(new_record)
print(kNN.predict_proba(new_record)) 

#[результат/вывод]: [[0.7 0.3]]
    

Здесь вероятность выживания составляет 0.3 – 30%.

Далее мы настраиваем алгоритм k-NN на поиск и использование 20 ближайших соседей, чтобы оценить состояние пассажира. Для наглядности выводим 20 первых соседей новой записи с помощью импортированного метода kneighbors. Реализация выглядит следующим образом:

        nbrs = knn.kneighbors(new_record)
maxDistance = np.max(nbrs[0][0])

fig, ax = plt.subplots(figsize=(10, 8))
sns.scatterplot(x = 'Age', y = 'Fare', style = 'Survived', 
                hue='Survived', data=train_df, alpha=0.3, ax=ax)
sns.scatterplot(x = 'Age', y = 'Fare', style = 'Survived', 
                hue = 'Survived', 
                data = pd.concat([train_df.loc[0:0, :], train_df.loc[nbrs[1][0] + 1,:]]), 
                ax = ax, legend=False)
ellipse = Ellipse(xy = new_record.values[0], 
                  width = 2 * maxDistance, height = 2 * maxDistance,
                  edgecolor = 'black', fc = 'None', lw = 1)
ax.add_patch(ellipse)
ax.set_xlim(.25, .29)
ax.set_ylim(0, .03)

plt.tight_layout()
plt.show()
    

Результат работы кода:

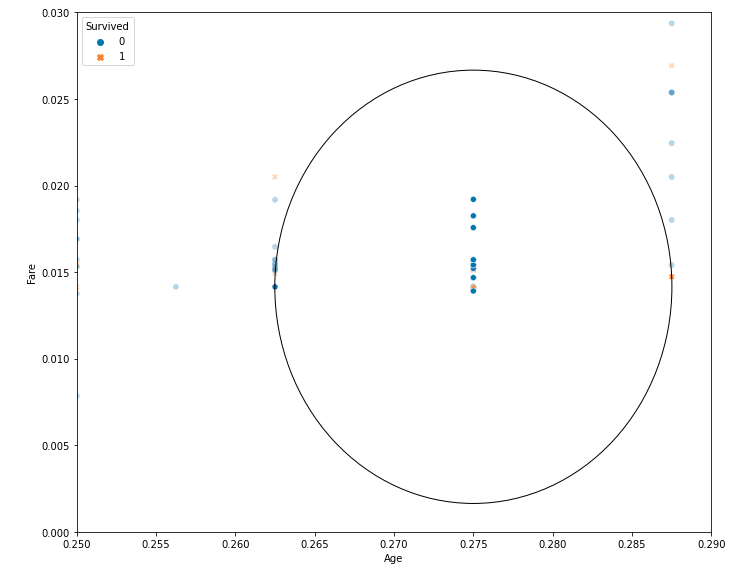
Как видите, на графике показаны 20 ближайших соседей, 14 из которых связаны с теми, кто не выжил (вероятность 0,7 – 70%), а 6 связаны с выжившими (вероятность 0,3 – 30%).

Мы можем просмотреть первые 20 ближайших соседей для заданных параметров при помощью следующего кода:

        nbrs = knn.kneighbors(new_record)
nbr_df = pd.DataFrame({'Age': X.iloc[nbrs[1][0], 0], 
                         'Fare': X.iloc[nbrs[1][0], 1],
                         'Survived': y.iloc[nbrs[1][0]]})
nbr_df
    

Результатом будет таким:

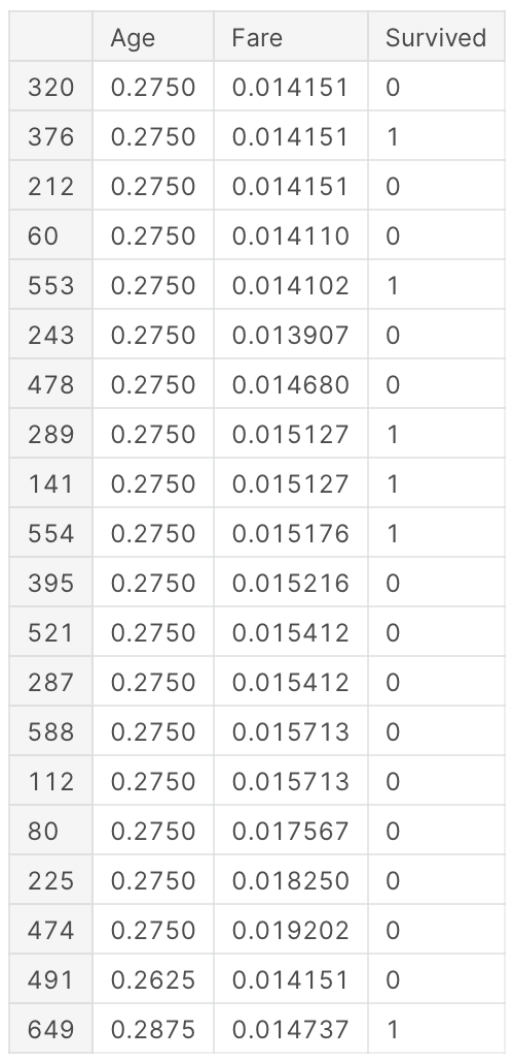
Выбор Оптимального значения для k-NN

Не существует конкретного способа определить наилучшее значение для k, поэтому нам нужно попробовать несколько значений, чтобы найти лучшее из них. Но чаще всего наиболее предпочтительным значением для k является 5:

• Низкое значение k, например, 1 или 2, может привести к эффекту недообучения модели.
• Высокое значение k на первый взгляд выглядит приемлемо, однако возможны трудности с производительностью модели, а также повышается риск переобучения.
  

Преимущества и Недостатки

Преимущества:

• Алгоритм прост и легко реализуем.

• Не чувствителен к выбросам.

• Нет необходимости строить модель, настраивать несколько параметров или делать дополнительные допущения.

• Алгоритм универсален. Его можно использовать для обоих типов задач: классификации и регрессии.

Недостатки:

• Алгоритм работает значительно медленнее при увеличении объема выборки, предикторов или независимых переменных.

• Из аргумента выше следуют большие вычислительные затраты во время выполнения.

• Всегда нужно определять оптимальное значение k.

В заключение

Метод k-ближайших соседей (k-nearest neighbors) – это простой алгоритм машинного обучения с учителем, который можно использовать для решения задач классификации и регрессии. Он прост в реализации и понимании, но имеет существенный недостаток – значительное замедление работы, когда объем данных растет.

Хочу освоить алгоритмы и структуры данных, но сложно разобраться самостоятельно. Что делать?

Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:

• изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
• научитесь применять алгоритмы и структуры данных при разработке программ;
• подготовитесь к техническому собеседованию и продвинутой разработке.

Курс подходит как junior, так и middle-разработчикам.