Задача 1: Газон
Перед коттеджем Ивана Ивановича есть газон – его можно считать плоскостью, на которой в каждой точке с целыми координатами растет один пучок травы. Однажды владелец купил новую газонокосилку, и в качестве тест-драйва подстриг прямоугольный участок газона. Стороны этого участка параллельны осям координат, а две противоположные вершины расположены в точках (x1, y1) и (x2, y2). При этом пучки травы, находящиеся на границе этого прямоугольника, также были подстрижены. После стрижки владелец установил на газоне поливальную установку. Она находится в точке с координатами (x3, y3) и имеет радиус действия r. Таким образом, установка начала поливать все пучки, расстояние, от которых до точки (x3, y3) не превышает r. Напишите программу, которая поможет Ивану Ивановичу определить, сколько пучков травы оказалось и подстрижено, и полито.

Формат входных данных
- В первой строке содержатся четыре целых числа x1, x2, y1, y2 (−100000 ≤ х1 < х2 ≤ 100000, −100000 ≤ y1 < y2 ≤ 100000).
- Вторая строка содержит три целых числа x3, y3, r (−100000 ≤ x3, y3 ≤ 100000, 1 ≤ r ≤ 100000.
Формат выходных данных
Целое число (количество подстриженных и политых пучков травы).
Пример ввода:
0 0 5 4
4 0 3
Вывод:
14
Решение
Сначала прямые, на которых расположены пучки травы, нужно разделить на группы в зависимости от их положения относительно осей абсцисс и ординат. Затем для каждой группы находим пересечение этих прямых с окружностью − областью, которую орошает поливальная установка. Если такие точки пересечения существуют, подсчитать количество постриженных и политых пучков травы для них можно с помощью простой операции − нахождения целой части числа. После этого все полученные числа складываются, и полученный результат будет ответом на задачу.
Время работы такого решения равно O(r), то есть оно пропорционально радиусу окружности (области полива) и не зависит от количества пучков травы или прямых.
Первый вариант решения – краткий:
from math import sqrt
def get_overlap(x, left, right):
return max(0, min(right, x) - max(left, x) + 1)
x1, y1, x2, y2 = map(int, input().split())
x3, y3, r = map(int, input().split())
count = 0
for y in range(y3 - r, y3 + r + 1):
for x in range(x3 - r, x3 + r + 1):
if sqrt((x - x3)**2 + (y - y3)**2) <= r:
count += get_overlap(x, x1, x2) * get_overlap(y, y1, y2)
print(count)
Второй вариант – быстрый:
from math import sqrt
def kol(x: int, z1: int, z2: int) -> int:
min = y1
max = y2
if x < x1 or x > x2 or z1 > y2 or z2 < y1:
return 0
else:
min = y1
if z1 > y1:
min = z1
max = y2
if z2 < y2:
max = z2
return max - min + 1
x1, y1, x2, y2 = map(int, input().split())
x3, y3, r = map(int, input().split())
count = kol(x3, y3 - r, y3 + r)
y = r
for x in range(1, r):
while sqrt(x**2 + y**2) > sqrt(r**2):
y -= 1
count += kol(x3 + x, y3 - y, y3 + y) + kol(x3 - x, y3 - y, y3 + y)
count += kol(x3 + r, y3, y3) + kol(x3 - r, y3, y3)
print(count)
Задача 2: Оптимальная стратегия
Два пирата придумали новую игру: выложили на стол в ряд все пиастры, и договорились, что во время очередного хода игрок может взять 1 монету либо справа, либо слева. Игра заканчивается, когда все монеты разобраны.
Оба пирата стремятся выиграть, и поэтому они будут брать монеты в соответствии с оптимальной стратегией. Разница между жадным алгоритмом и оптимальной стратегией выглядит так:
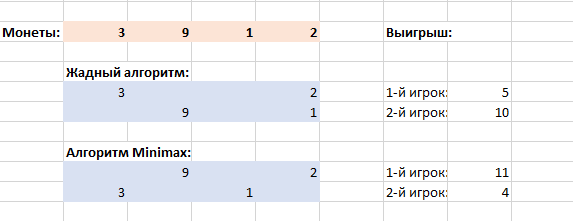
Напишите программу для определения победителя и суммы его выигрыша при условии, что оба участника играют оптимально, а монеты имеют разное достоинство.
Примеры ввода и вывода:
8
2 1 8 4 9 2 4 9
Победил 1-й игрок, сумма выигрыша: 28
6
8 8 8 8 8 8
Ничья: игроки выиграли по 24
2 1 3 2 9 1 2 3 1
Победил 2-й игрок, сумма выигрыша: 9
Решение
Эту задачу можно решить двумя способами.
Способ 1 – рекурсия с мемоизацией
Во время хода у каждого игрока есть две опции:
1. Взять монету Ci слева – тогда оппонент выберет монету Ci+1 или Cj. При этом каждый игрок стремится сделать выбор, который оставить противника с минимальной прибылью, то есть игрок может забрать монету Ci + min(function(i+2, j), function(i+1, j-1) ) где [i+2,j] – диапазон монет, доступных игроку, если противник выберет монету Ci+1, a[i+1,j-1] – монеты, доступные игроку в том случае, если оппонент возьмет монету справа, Cj.
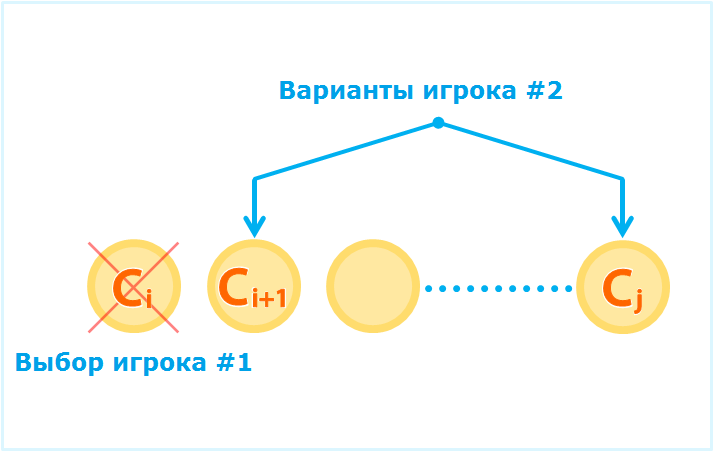
2. Взять монету Cj справа – в этом случае противник выберет либо Ci слева, либо Cj-1 справа. Чтобы оставить противника с минимальной прибылью, игрок возьмет монету, соответствующую условию Cj + min(function(i+1, j-1), function(i, j-2) ), где [i,j-2] – монеты, доступные пользователю, если противник выберет монету справа, а [i+1,j-1] – монеты, доступные при выборе Ci.
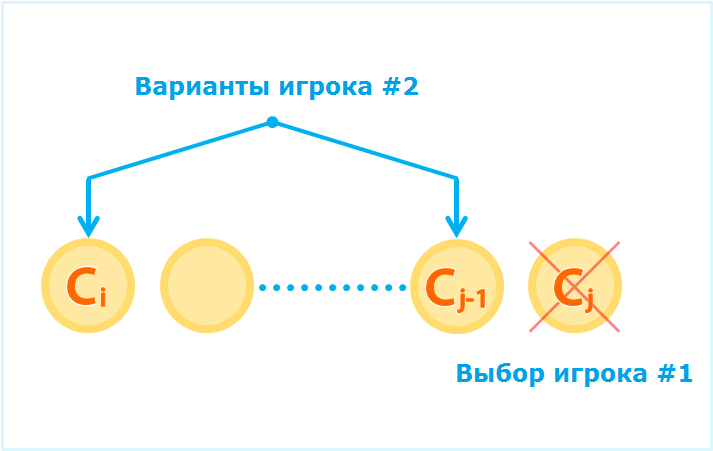
Таким образом, рекурсивный случай выглядит так:
function(i, j) = max(Ci + min(function(i+2, j), function(i+1, j-1) ),
Cj + min(function(i+1, j-1), function(i, j-2) ))
Граничные случаи:
function(i, j) = Ci, если j == i
function(i, j) = max(Ci, Cj), еслиj == i + 1
Код решения с рекурсией:
def winner_is(coins, n):
memo_dict = {}
def options(i, j):
if i > j or i >= n or j < 0:
return 0
k = (i, j)
if k in memo_dict:
return memo_dict[k]
opt1 = coins[i] + min(options(i + 2, j), options(i + 1, j - 1))
opt2 = coins[j] + min(options(i + 1, j - 1), options(i, j - 2))
memo_dict[k] = max(opt1, opt2)
return memo_dict[k]
return options(0, n - 1)
n = int(input())
coins = list(map(int, input().split()))
result = winner_is(coins, n)
if result > (sum(coins) - result):
print(f'Победил 1-й игрок, сумма выигрыша: {result}')
elif result < (sum(coins) - result):
print(f'Победил 2-й игрок, сумма выигрыша: {result}')
else:
print(f'Ничья: игроки выиграли по {result}')
Способ 2 – динамическое программирование
Алгоритм решения:
Нужно создать матрицу размера n x n.
В цикле рассматриваются элементы i и j на всех возможных позициях. Элементы разделены определенным количеством других элементов – дистанцией. В зависимости от результатов сравнения присваиваем значения переменным x, y, z:
- если i+2 <=j, то x равно matrix[i+2][j], в противном случае x = 0;
- если i+1 <=j-1, то y = matrix[i+1][j-1] , в противном случае y = 0;
- если i <= j-2, то z = matrix[i][j-2] , в противном случае z = 0.
Присваиваем matrix[i][j] максимальное значение из двух выражений – coins[i] + min(x, y) и coins[j] + min(y, z). Ответ – в matrix[0][n – 1].
Код решения с динамическим программированием:
def winner_is(coins, n):
matrix = [[0 for i in range(n)] for i in range(n)]
for distance in range(n):
for j in range(distance, n):
i = j - distance
x = 0
if i + 2 <= j:
x = matrix[i + 2][j]
y = 0
if i + 1 <= j - 1:
y = matrix[i + 1][j - 1]
z = 0
if i <= j - 2:
z = matrix[i][j - 2]
matrix[i][j] = max(coins[i] + min(x, y), coins[j] + min(y, z))
return matrix[0][n - 1]
n = int(input())
coins = list(map(int, input().split()))
result = winner_is(coins, n)
if result > (sum(coins) - result):
print(f'Победил 1-й игрок, сумма выигрыша: {result}')
elif result < (sum(coins) - result):
print(f'Победил 2-й игрок, сумма выигрыша: {result}')
else:
print(f'Ничья: игроки выиграли по {result}')
Задача 3. Эскалатор
Станция метрополитена оснащена эскалатором. Пусть N человек бегут вниз по эскалатору, причем i-й пробегает одну ступеньку за ti секунд. Техника безопасности на эскалаторе запрещает «обгоны», то есть если человек A в процессе бега догнал человека B, который бежит с более низкой скоростью, то далее, до конца эскалатора, человек A бежит со скоростью человека B. Однако ступени эскалатора таковы, что на них может помещаться несколько человек одновременно.
Напишите программу, которая поможет работникам станции рассчитать, когда закончит свой бег по эскалатору каждый бегущий человек.
Формат входных данных
В первой строке программа получает число N (1 ≤ N ≤ 105). В последующих строках перечислены пары чисел ti, wi(1 ≤ ti, wi ≤ 106) – время пробега одной ступени и количество ступеней до конца эскалатора для i-того человека.
Формат выходных данных
Время в секундах, через которое i-й человек сойдет с эскалатора.
Пример ввода:
3
2 10
3 11
1 12
Вывод:
20
33
33
Решение
- Создаем массив order из индексов [0..n-1] для хранения порядка отсортированных людей.
- Вызываем быструю сортировку qs, которая сортирует людей по скорости, записывая индексы отсортированных людей в массив order.
- После сортировки для каждого человека вычисляем максимум из его собственного времени выхода и времени выхода предыдущего человека (учитывая, что обгонять нельзя).
В итоге мы получаем время для каждого человека с учетом правил эскалатора:
import random
n = int(input())
times = []
speeds = []
for i in range(n):
a, b = map(int, input().split())
times.append(a)
speeds.append(b)
order = list(range(n))
res = [a * b for a, b in zip(times, speeds)]
def qs(l, r):
if l >= r:
return
i = l
j = r
x = speeds[order[random.randint(l, r-1)]]
while i <= j:
while speeds[order[i]] < x:
i += 1
while speeds[order[j]] > x:
j -= 1
if i <= j:
order[i], order[j] = order[j], order[i]
i += 1
j -= 1
qs(l, j)
qs(i, r)
qs(0, n-1)
for i in range(1, n):
res[order[i]] = max(res[order[i]], res[order[i-1]])
for x in res:
print(x)
Задача 4: Вырубка деревьев
Фермер решил вырубить некоторые деревья, растущие перед его домом. Деревья перед домом посажены в ряд, всего там растет n деревьев, расстояния между соседними деревьями одинаковы. После вырубки перед домом должно остаться m деревьев, и расстояния между соседними деревьями должны быть одинаковыми. Помогите фермеру выяснить, сколько существует способов вырубки деревьев.
Требуется написать программу, которая по заданным числам n и m определит, сколько существует способов вырубки некоторых из n деревьев так, чтобы после вырубки осталось m деревьев, и соседние деревья находились на равном расстоянии друг от друга. Так, например, выглядят варианты для m = 5 и n = 3:
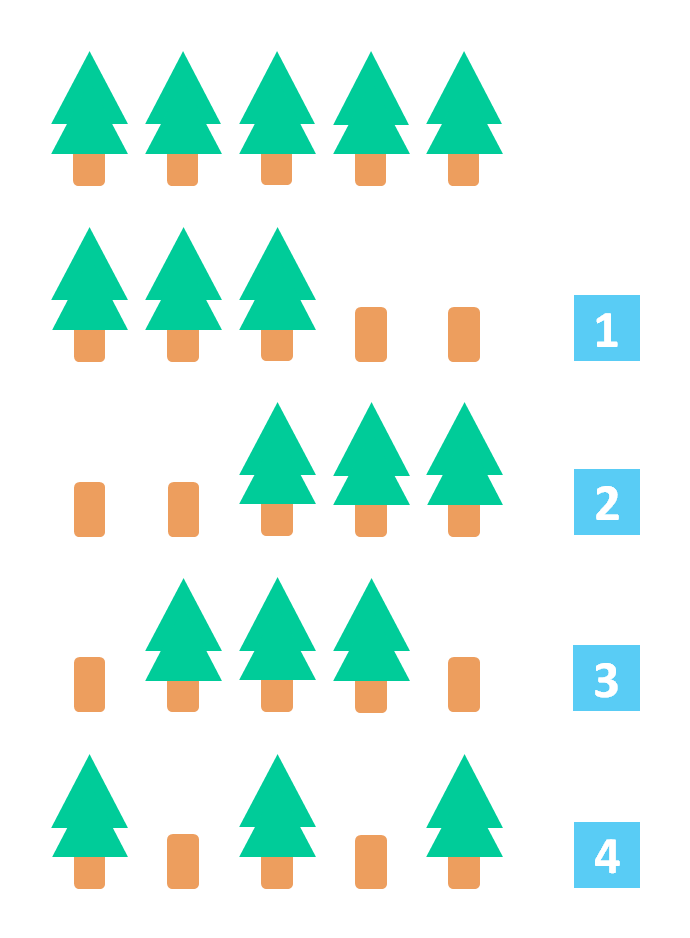
Пример ввода:
125 25
Вывод:
265
Решение
Обозначим расстояние между деревьями после вырубки d. Тогда существует n – d х (m – 1) – m + 1 способов вырубить деревья. Чтобы найти все варианты, нужно просуммировать способы по всем d. Кроме того, нужно учесть 2 частных случая – когда количество оставшихся после вырубки деревьев равно 0 или 1.
Вариант решения 1:
n, m = list(map(int, input().split()))
trees = 0
if m == 0:
trees = 1
elif m == 1:
trees = n
else:
for d in range(1, n):
trees += (n - d) // (m - 1)
print(trees)
Вариант решения 2:
n, m = map(int, input().split())
trees = 0
if m == 0:
trees = 1
elif m == 1:
trees = n
else:
for d in range(1, (n - 1) // (m - 1) + 1):
trees += n - (m - 1) * d
print(trees)
Задача 5. Симпатичные узоры
Мастер-плиточник выкладывает на полу размером m x n узоры из черных и белых плиток размером 1 х 1 метр. Проблема в том, что каждый новый клиент хочет, чтобы узор был уникальным, и не повторял предыдущие заказы мастера. Кроме того, узор должен быть симпатичным. Узор является симпатичным, если в нем нигде не встречается квадрата 2×2 метра, полностью покрытого плитками одного цвета.Это пример симпатичных узоров:
А на этой картинке – образцы несимпатичных:

Напишите программу, которая определит, сколько заказов сможет выполнить мастер при заданных ограничениях.
Решение:
Задача сводится к подсчету числа способов разбиения множества из n элементов на m непересекающихся подмножеств, и решается с помощью динамического программирования.
Основная идея:
Каждое подмножество кодируется битовой маской длины n бит. Если i-й бит установлен в 1, значит i-й элемент входит в это подмножество.
В adj_mask[prv][cur] хранится информация о том, совместимы ли подмножества prv и cur (то есть не пересекаются ли они). Это проверяется заранее для всех пар подмножеств.
Для каждого числа подмножеств k от 1 до m, мы заполняем массив dp[k][mask] – число способов разбиений на k подмножеств, где последнее подмножество имеет битовую маску mask.
Переход от k-1 подмножеств к k происходит с помощью adj_mask:
dp[k][cur] += dp[k-1][prv], если подмножества prv и cur совместимы.
В итоге ответом служит сумма по всем битовым маскам в dp[m-1][mask].
Таким образом, методом динамического программирования подсчитывается число разбиений заданного множества на m подмножеств.
max_height = 5
max_mask = (1 << max_height) - 1
def get_bit(num, bit):
return num & (1 << bit) != 0
def precalc_matrix(adj_mask, n):
for prv in range(max_mask + 1):
for cur in range(max_mask + 1):
is_comp = True
for bit in range(n - 1):
sum = get_bit(prv, bit) + get_bit(prv, bit + 1) + get_bit(cur, bit) + get_bit(cur, bit + 1)
if sum == 0 or sum == 4:
is_comp = False
break
adj_mask[prv][cur] = is_comp
def solve(dp, adj_mask, mask):
for mask in range(mask + 1):
dp[0][mask] = 1
for k in range(1, m):
for prv in range(mask + 1):
for cur in range(mask + 1):
if adj_mask[prv][cur]:
dp[k][cur] += dp[k - 1][prv]
n, m = map(int, input().split())
if n > m:
n, m = m, n
mask = (1 << n) - 1
adj_mask = [[False] * (max_mask + 1) for _ in range(max_mask + 1)]
dp = [[0] * (max_mask + 1) for _ in range(35)]
precalc_matrix(adj_mask, n)
solve(dp, adj_mask, mask)
print(sum(dp[m - 1]))



Комментарии