Что же за зверь такой, эти числовые последовательности?

Говоря формальным языком, под последовательностью понимается отображение из множества натуральных чисел во множество произвольной природы. Фактически мы перенумеровываем элементы некоторого множества. В курсе математического анализа наиболее важными являются числовые последовательности, т.е. «перенумерация» некоторого подмножества из множества вещественных чисел. Если говорить сухим математическим языком, такое соотношение записывается следующим образом:

Для наглядности мы проиллюстрируем на следующем примере:

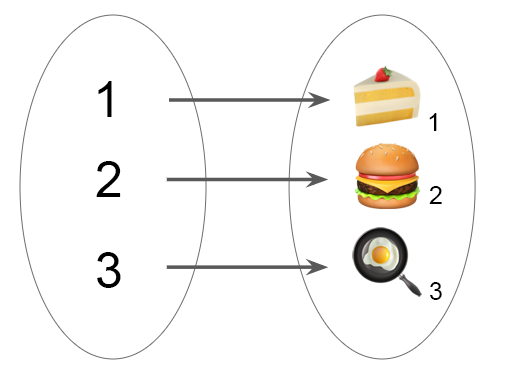
Зачем я должен об этом знать?

Важнейшим понятием из теории числовых последовательностей является понятие предела. Для чего же в программировании может быть использован предел числовой последовательности? Давайте рассмотрим пример поиска логарифма.

Машина изначально умела только делать логические операции с числами, записанными в двоичной системе счисления, затем ее научили делать простейшие арифметические операции, но когда дело дошло до поиска значение «более сложных» функций, таких как логарифм, в дело пошли числовые последовательности, а именно последовательности сумм рядов, которые позволяют с той или иной точностью понять, чему же равен логарифм того или иного числа. А логарифм, в свою очередь, используется, к примеру, в нейросетях.

Но об этом чуть позже.

Как же нам определить предел последовательности?

Как же определяется предел числовой последовательности? Математическим языком это записывается следующим образом:

Число a является пределом числовой последовательности X_n , если выполняется следующие условие:

Звучит сложно для восприятия, не правда ли?

Давайте рассмотрим визуализацию сходящейся числовой последовательности, которая выглядит следующим образом

Чтобы было нагляднее понимать это определение, можно представить, что ε — это ширина трубки, которую мы можем уменьшать сколько угодно, в любом случае найдется такое N, начиная с которого все, что справа от него, будет находиться в этой трубке.

Здесь изображена конкретная ε - трубка, но видно, что каково бы ни было число ε > 0, всегда найдется N, от него зависящий, что начиная с этого номера значения последовательности x_n отличаются от 1 не более чем на ε.

Рассмотрим еще примеры

Между тем расходящиеся числовые последовательности встречаются намного чаще. Давайте домножим рассмотренную выше последовательность на «переключатель» (-1)ⁿ. Получаем последовательность:

Вот ее визуализация:

У этой последовательности есть две точки «накопления» её элементов – «1» и «-1». Мы видим, что, например, для ε = 0,1 (см. чертёж) мы никогда не найдем такого N, что все точки последовательности, начиная с некоторого номера, будут попадать в интервал (a - ε; a + ε), где a -- произвольно заданное число. Все четные элементы попадают в верхнюю ε - окрестность, а все нечетные в нижнюю. Предела у этой последовательности нет.

Рассмотрим более хитрые примеры расходящихся числовых последовательностей. Изобразим, например:

У этой последовательности 5 точек накопления ее элементов (также известных, как частичные пределы).

Можно рассмотреть эту же последовательность, изображенную в виде точек. По оси абсцисс отложены номера элементов:

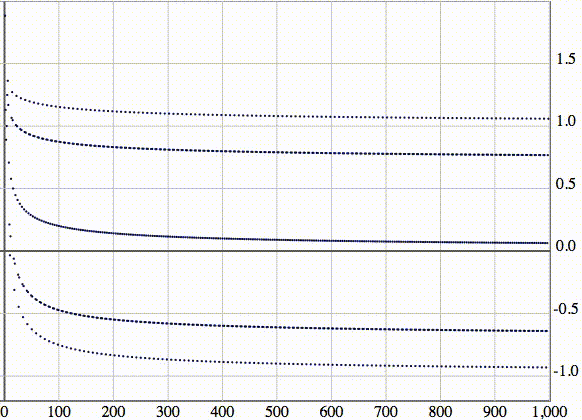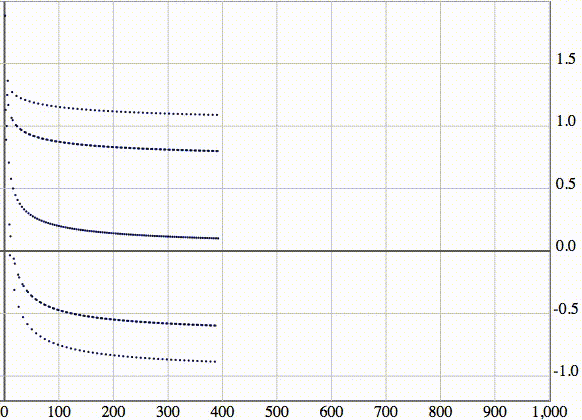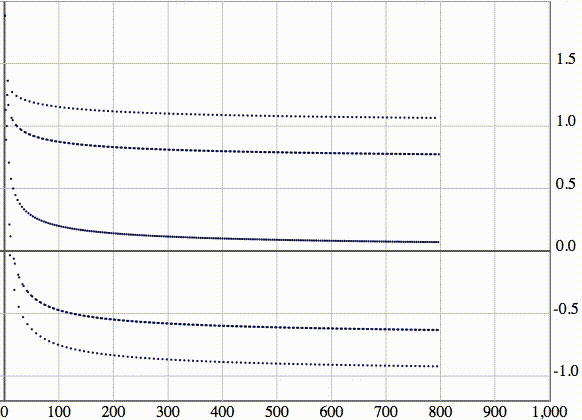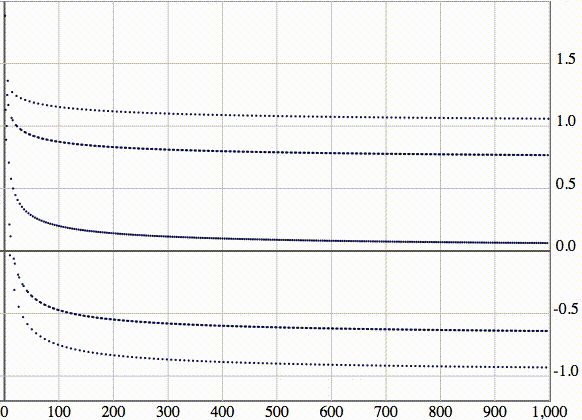
Рассмотрим последовательность с бесконечным числом точек накопления элементов (частичных пределов).

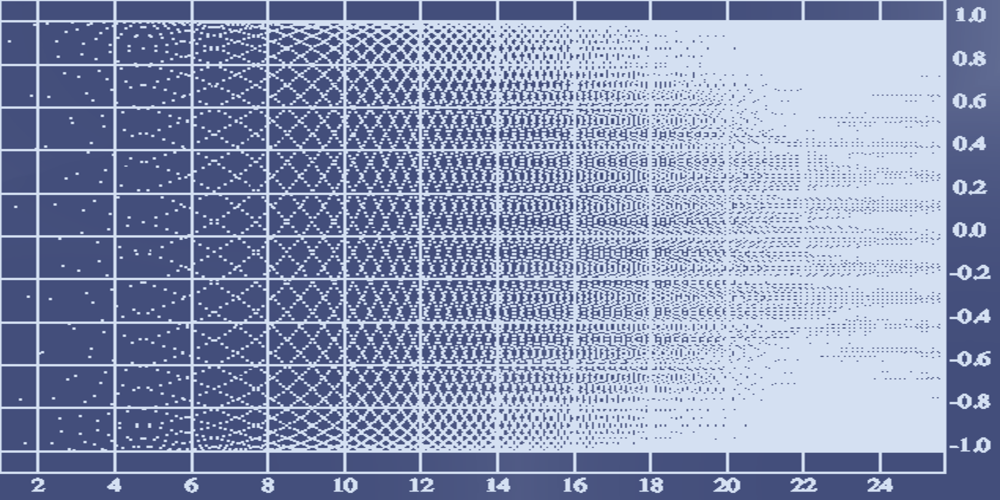
Как видно на визуализации, множество ее частичных пределов представляет из себя весь отрезок от -1 до 1:

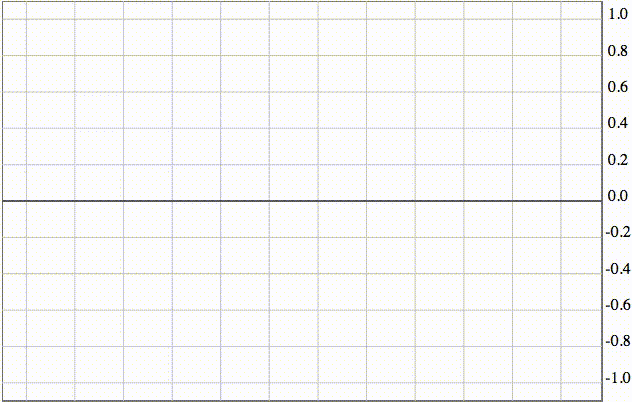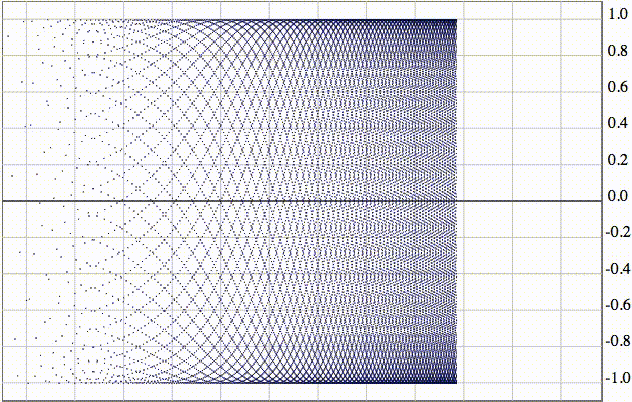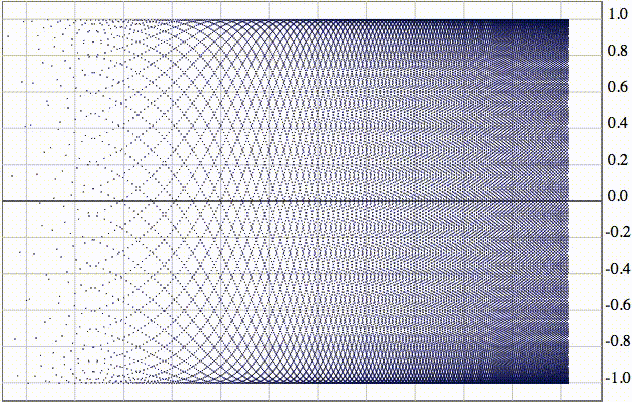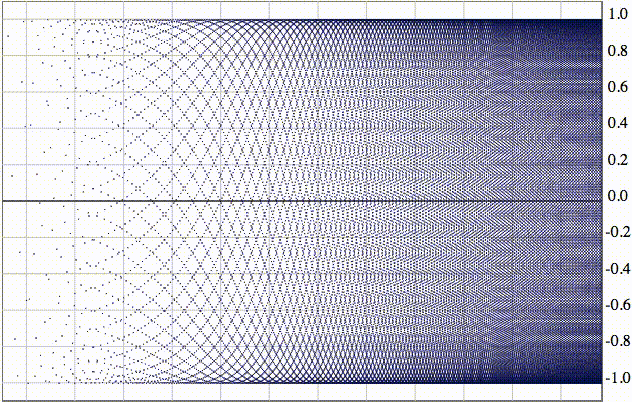
На анимации изображена логарифмическая шкала на 50 тысяч элементов.

Если рассмотреть эту последовательность в виде вертикальных отрезков, они плотно заполнят весь отрезок от -1 до 1.

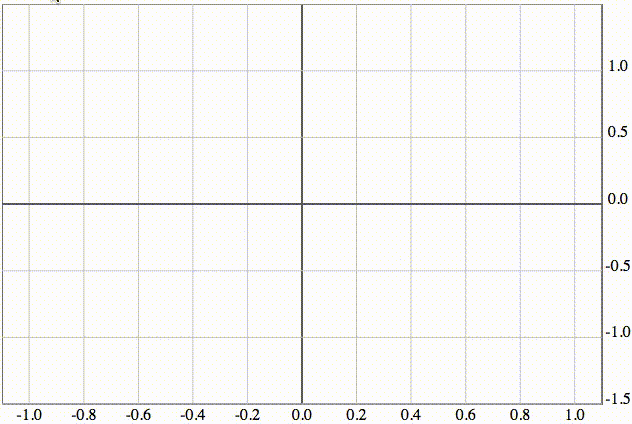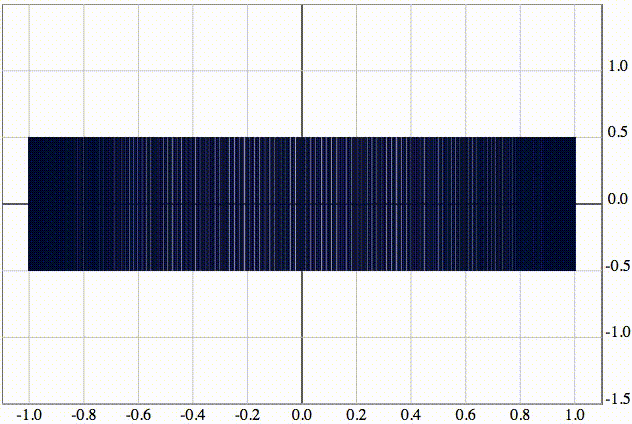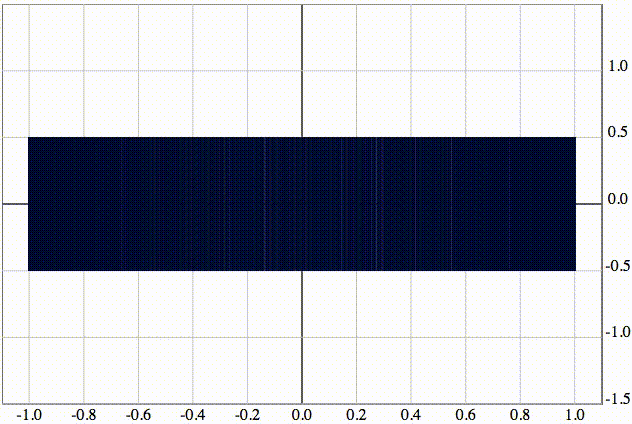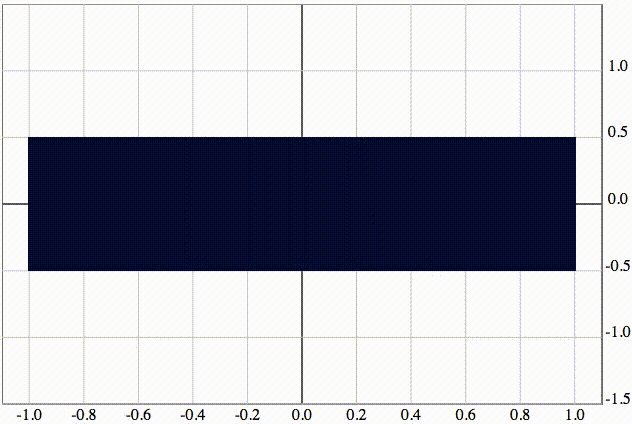
Изобразим числовую последовательность, включающую в себя все рациональные числа от 0 до 1. Множество ее частичных пределов представляет собой отрезок [0; 1].

Ее визуализация в логарифмической шкале будет выглядеть следующим образом:

Далее рассмотрим визуализации числовых последовательностей, сходящихся к числу  e :

Может быть, многие из вас знают, что последовательность s_n сходится к числу e гораздо быстрее, но насколько быстрее – представить не очень просто. В этом нам тоже помогут анимации. Давайте изобразим обе эти последовательности на одном графике:

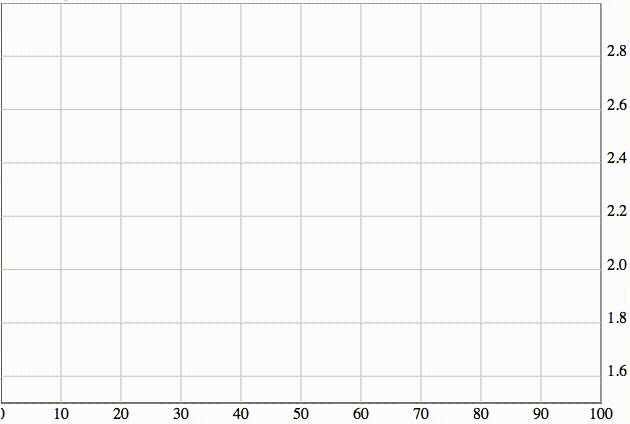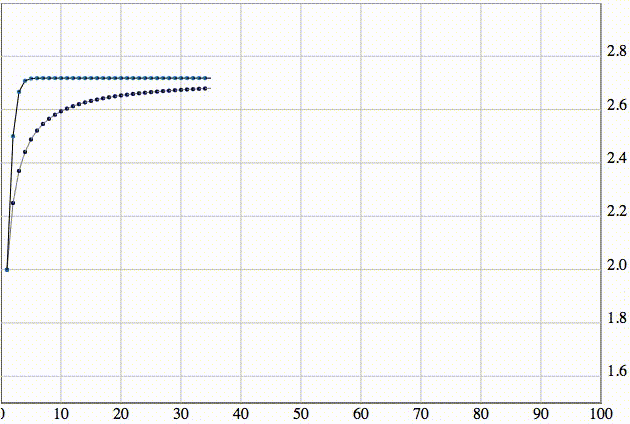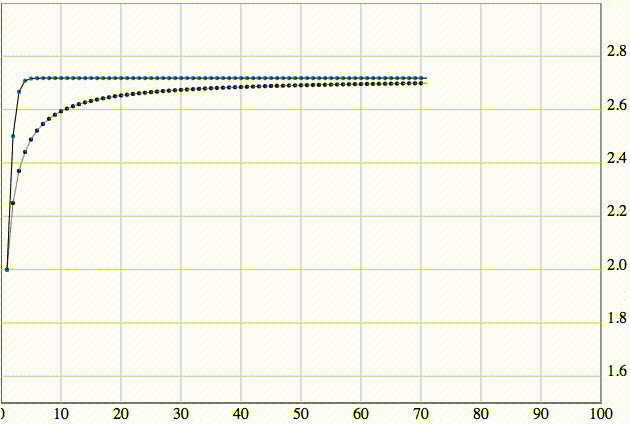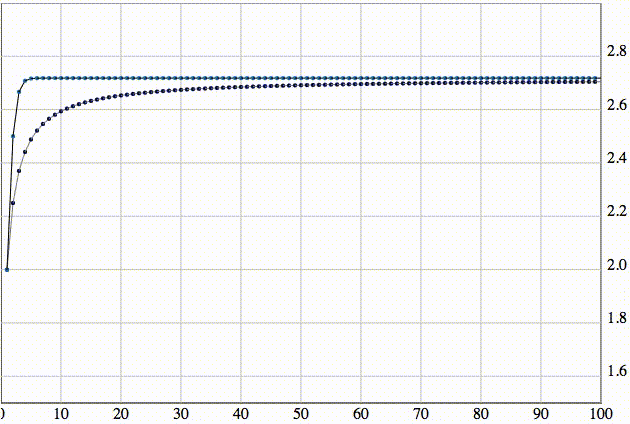
Зачем может пригодиться число e? В математике оно всплывает крайне часто, например, для поиска факториала.

И на десерт

В заключение рассмотрим последовательность, частичными пределами которой являются все дроби вида:

На графике она будет выглядеть следующим образом:

И в вертикальных отрезках:

Видно, что точка 0 тоже является частичным пределом.

                                                                        Продолжение следует...

Если вас заинтересовало наше иллюстративное объяснение темы числовых последовательностей, вы можете также посмотреть иллюстративный курс по математическому анализу.

Выражаем большую признательность за работу Алексею Никитину и Алексею Карпову.