Задача о прогуливающихся джентльменах

Эта задача – шестой эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую головоломку о Времени великих учёных. Головоломки публикуются по субботам и средам.

Задача о прогуливающихся джентельменах

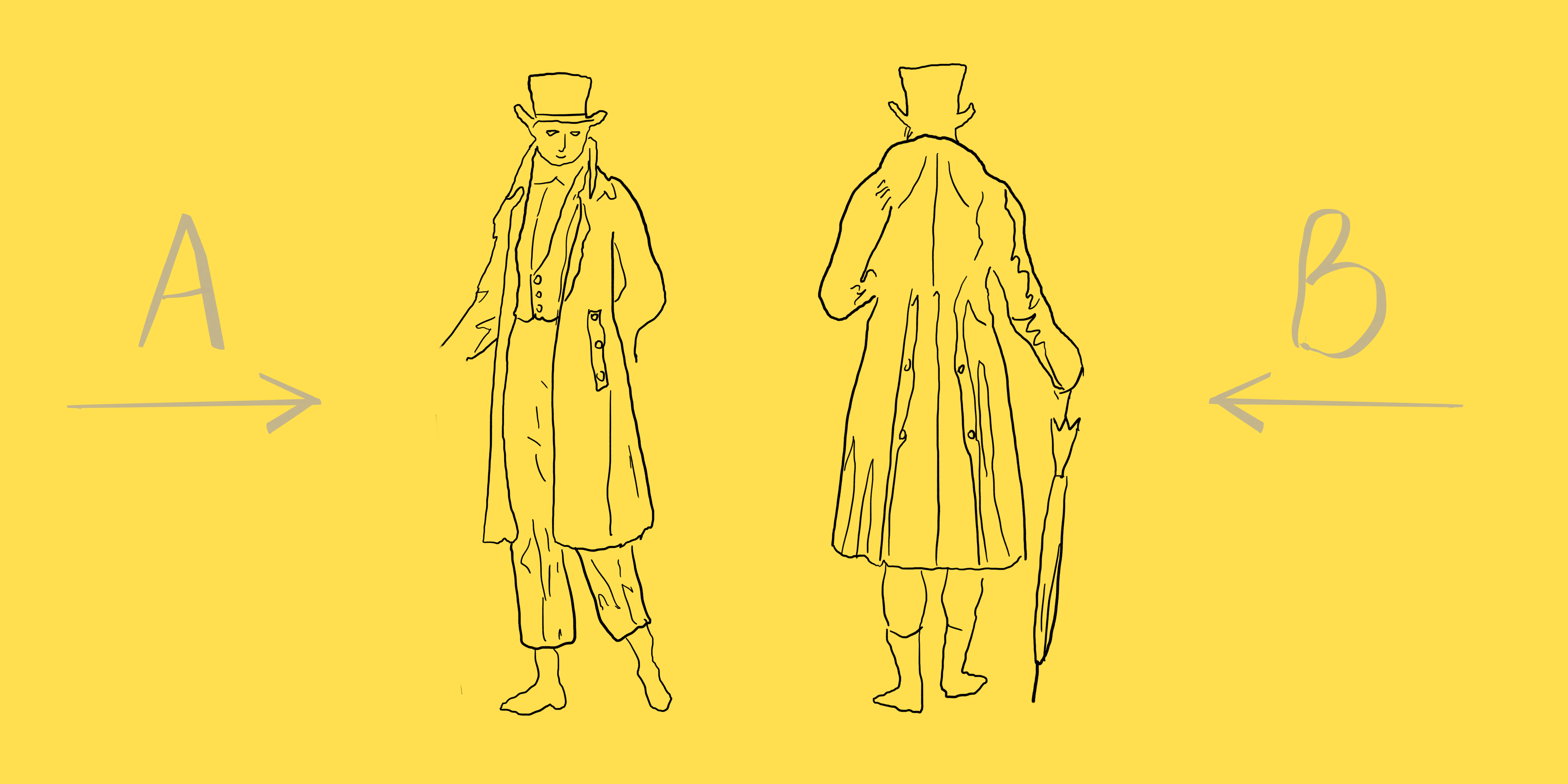
Два джентльмена одновременно начали прогулку из пунктов A и B, чтобы завершить её, соответственно, в пунктах B и A. В каждый момент времени скорости джентльменов равны по величине. Между A и B 1000 метров, через каждые 100 метров от главной аллеи отходят боковые тупиковые аллеи длиной 100 метров. Поравнявшись с боковой аллеей, джентльмен может пройти по ней туда-обратно либо её проигнорировать. Неизбежна ли встреча джентльменов?

Идеи и ответы можно обсудить в комментариях. Первого читателя, указавшего правильное решение, мы выделим при публикации следующей задачи (см. пример ниже).

Ответ и новая задача.

Решение задачи о Времени великих учёных

В общем виде проблема может быть сформулирована следующим образом. Задано n интервалов (b₁, d₁), ... , (b_n, d_n). В нашем случае b_i, d_i – даты рождения и смерти i-го человека в указателе (1 ≤ i ≤ n). Нужно найти интервал, который является пересечением наибольшего количества данных интервалов.

Последнее условие указывает на то, что все интервалы открыты, то есть не включают их конечные точки. Если di = bj, закрывающая скобка i-го интервала предшествует открывающей скобке j-го интервала. Если несколько интервалов имеют одну и ту же открывающую скобку, она должна учитываться для каждого из этих интервалов, то же самое верно для совпадающих закрывающих скобок.

Полезно визуализировать интервалы, изображённые на реальной временно́й шкале, как это сделано ниже на рисунке. Последовательность круглых скобок содержит ключ к эффективному решению проблемы. При сканировании последовательности слева направо число персон увеличивается на 1 на каждой открывающей скобке и уменьшается на 1 на закрывающей.

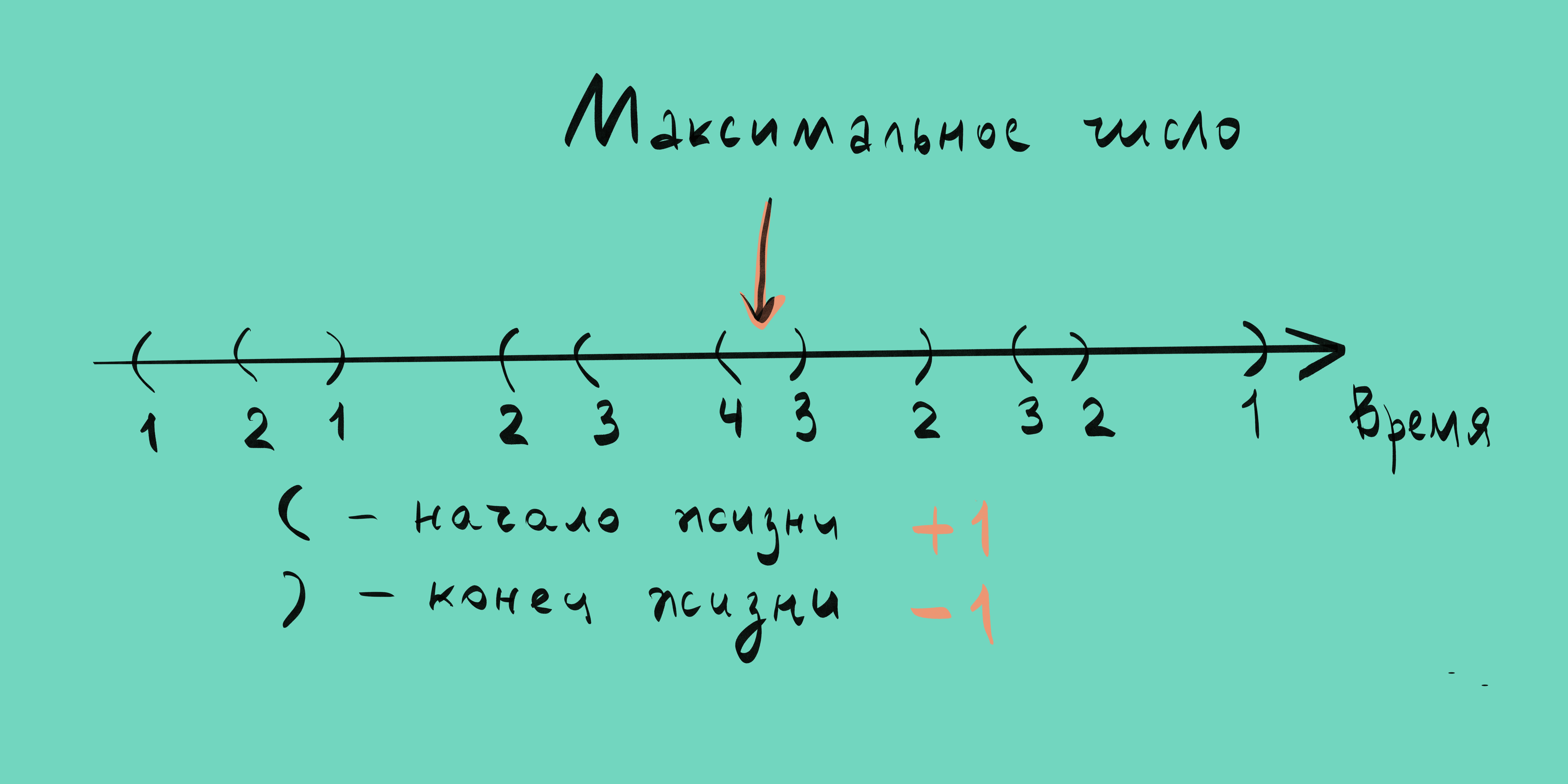
Таким образом, искомый интервал лежит между открывающей скобкой с максимальным значением счётчика и следующей за ней закрывающей скобкой.

К правильному ходу решения головоломки первым подобрался Тима Рейзин:

Данную задачу можно решить с помощью дерева отрезков с обновлением на отрезке. Для каждого ученого будем пробавляться единицу на интервала рождение – смерть. Потом найдём максимум во всем массиве. Легко реализовать, чтоб при поиске максимума также возвращался интервал максимума. Что же к последнему предложению, то можно создать в массиве две ячейки – для начала и конца года, в каждую из которых соответственно можно записывать начала и конца жизней, если они были в этом году. Ответом на задачу будет отрезок, на котором находится максимум.