Каждый Data Scientist знает, что фундаментальные знания статистики необходимы для успеха в его профессии. Поэтому мы прошерстили Интернет и нашли сорок вопросов по статистике, задаваемых аналитикам данных на собеседовании.
1. Как оценить статистическую значимость анализа?
Для оценки статистической значимости нужно провести проверку гипотезы. Сначала определяют нулевую и альтернативную гипотезы. Затем рассчитывают p – вероятность получения наблюдаемых результатов, если нулевая гипотеза верна. Наконец, устанавливают уровень значимости alpha. Если p < alpha, нулевая гипотеза отвергается – иными словами, анализ является статистически значимым.
2. Приведите три примера распределений с длинным хвостом. Почему они важны в задачах классификации и регрессии?

Три практических примера: степенной закон, закон Парето и продажи продуктов (например, продукты-бестселлеры против обычных).
При решении задач классификации и регрессии важно не забывать о распределении с длинным хвостом, поскольку редко встречающиеся значения составляют существенную часть выборки. Это влияет на выбор метода обработки выбросов. Кроме того, некоторые методики машинного обучения предполагают, что данные распределены нормально.
3. Что такое центральная предельная теорема, и почему она важна?
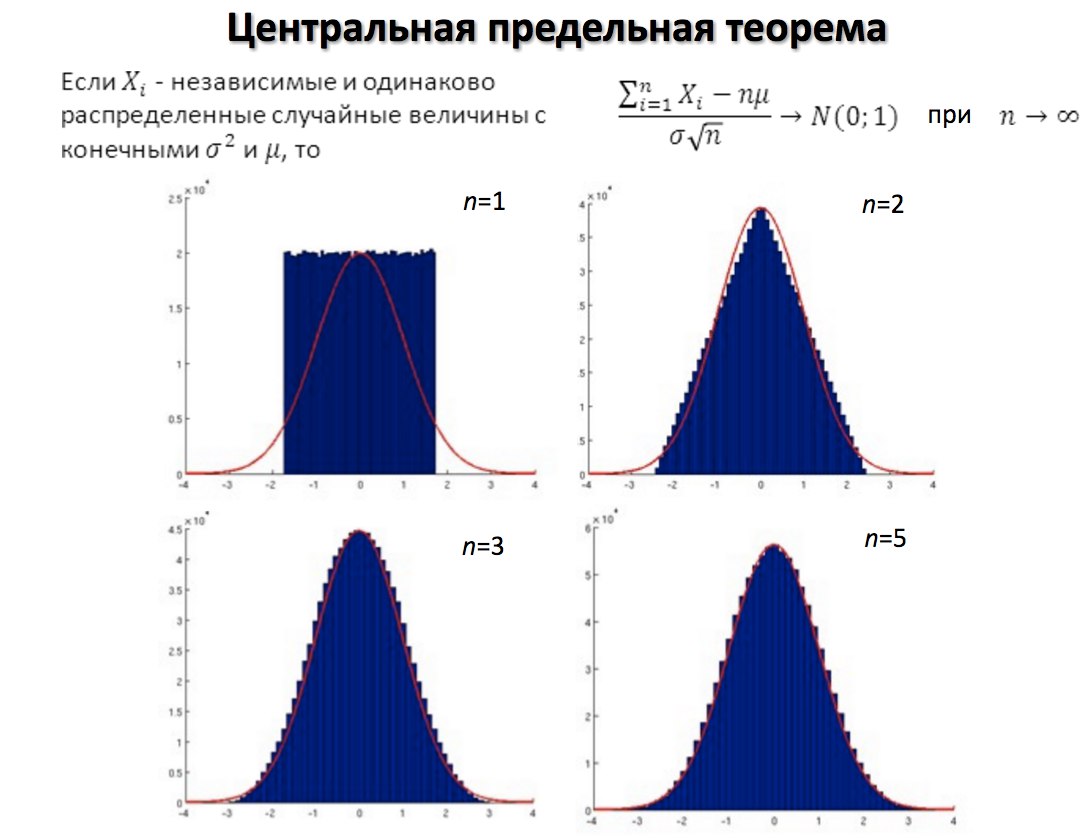
Центральная предельная теорема (ЦПТ) говорит о том, что сумма достаточно большого количества слабо зависимых случайных величин с примерно одинаковыми масштабами имеет распределение, близкое к нормальному.
Центральная предельная теорема важна, поскольку она используется при проверке гипотез и расчете доверительных интервалов.
4. Что такое статистическая мощность?
Статистическая мощность – это мощность бинарной гипотезы, то есть вероятность отклонения нулевой гипотезы, если альтернативная гипотеза верна.
5. Что такое ошибка отбора (в отношении данных), и почему она важна? Как предварительная обработка данных может ухудшить ситуацию?
Ошибка отбора – это выбор для анализа людей, групп или данных методом, не обеспечивающим должную рандомизацию, в результате чего выборка не является репрезентативной.
Существуют следующие виды ошибок отбора:
- ошибка выборки: выборка, полученная не в результате случайного отбора.
- интервал времени: выбор особого интервала времени, поддерживающего желаемый вывод – например, исследование продаж перед Рождеством.
- воздействие: включает клиническую уязвимость, протопатическую ошибку и ошибку показателей (подробнее см. здесь).
- ошибка данных: выборочное представление фактов, избирательный подход, выборочное цитирование.
- ошибка истощения: включает «ошибку выжившего», когда в анализ включаются только те, кто «пережил» длительный процесс и «ошибку неудачников», когда в анализ включаются только те, кто потерпел неудачу.
Обработка пропущенных данных может усилить влияние ошибок отбора. Например, если вы заменяете значения null на средние значения, вы добавляете в данные ошибку, поскольку считаете, что данные не имеют такого разброса, который они могут иметь на самом деле.
6. Дайте простой пример того, как постановка экспериментов может помочь ответить на вопрос о поведении. Как экспериментальные данные контрастируют с данными наблюдений?
Данные наблюдений получаются от исследования наблюдений, когда мы наблюдаем значения нескольких переменных и определяем, есть ли между ними корреляция.
Экспериментальные данные получаются от исследования экспериментов, когда мы контролируем некоторые переменные и сохраняем их значения неизменными, определяя их влияние на результат.

Вот пример постановки эксперимента: разбейте группу на две части. Контрольная группа живет, как обычно. Тестовую группу просят выпивать по бокалу вина каждый вечер на протяжении 30 дней. После этого можно исследовать, как вино влияет на сон.
7. Является ли подстановка средних значений вместо пропусков допустимым? Почему?
Подстановка средних значений – это метод замены пропусков в наборе данных средними значениями соответствующих признаков.
Как правило, подстановка средних значений – плохой метод, поскольку он не принимает во внимание корреляцию между признаками.
Например, у нас есть таблица с данными о возрасте и уровне физической формы, и для 80-летнего человека уровень физической формы пропущен. Если мы возьмем средний уровень физической формы для всех возрастов от 15 до 80 лет, очевидно, что наш 80-летний получит более высокий уровень, чем имеет на самом деле.
Кроме того, подстановка средних значений уменьшает дисперсию данных и повышает уровень ошибок. Это приводит к менее точной модели и более узким доверительным интервалам.
8. Что такое выброс и внутренняя ошибка? Объясните, как их обнаружить, и что бы вы делали, если нашли их в наборе данных?
Выброс (англ. outlier) – это значение в данных, существенно отличающееся от прочих наблюдений.
В зависимости от причины выбросов, они могут быть плохими с точки зрения машинного обучения, поскольку ухудшают точность модели. Если выброс вызван ошибкой измерения, важно удалить его из набора данных. Есть пара способов обнаружения выбросов.
1) Z-оценка/стандартные отклонения: если мы знаем, что 99.7% данных в наборе лежат в пределах тройного стандартного отклонения, мы можем найти элементы данных, выходящие за эти пределы. Точно так же, мы можем рассчитать z-оценку каждого элемента, и если она равна +/- 3, это выброс.
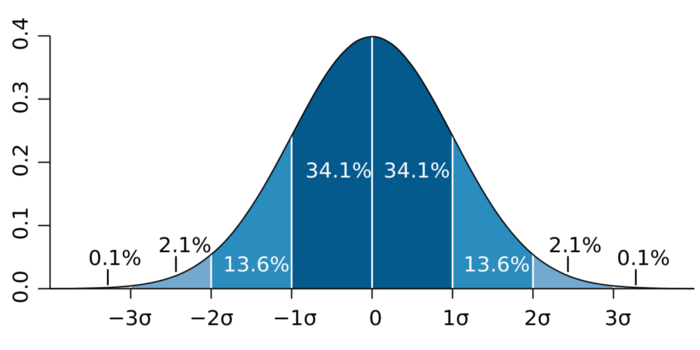
2) Межквартильное расстояние (Inter-Quartile Range, IQR) – концепция, положенная в основу ящиков с усами (box plots), которую также можно использовать для нахождения выбросов. МКР – это расстояние между 3-м и 1-м квартилями. После его расчета можно считать значение выбросом, если оно меньше Q1-1.5*IQR или больше Q3+1.5*IQR. Это составляет примерно 2.7 стандартных отклонений.
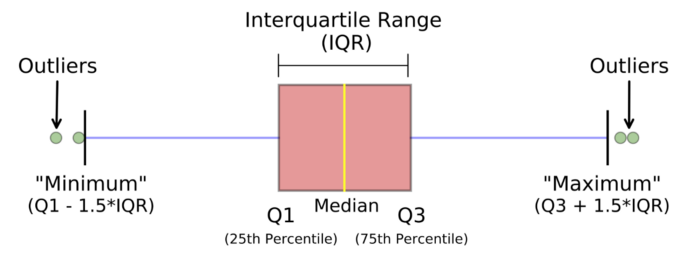
Другие методы включают кластеризацию DBScan, Лес Изоляции и устойчивый случайно-обрубленный лес.
Внутренняя ошибка (inlier) – это наблюдение, лежащее в пределах общего набора данных, но необычное либо ошибочное. Поскольку оно находится там же, где остальные данные, его труднее идентифицировать, чем выброс. Внутренние ошибки обычно можно просто удалить из набора данных.
9. Как вы обрабатываете пропуски? Какие методы подстановки вы рекомендуете?
Существует несколько способов обработки пропущенных данных:
- удаление строк с пропущенными данными;
- подстановка среднего значения, медианы или моды;
- присваивание уникального значения;
- предсказание пропущенных значений;
- использование алгоритма, допускающего пропуски – например, случайный лес.
Лучший метод – удалить строки с пропусками, поскольку это гарантирует, что мы не добавим никаких ошибок или сдвигов, и, в конечном счете, получим точную и надежную модель. Однако, этот метод можно использовать лишь в тех случаях, когда данных много, а процент пропусков невысок.
10. Есть данные о длительности звонков в колл-центр. Разработайте план кодирования и анализа этих данных. Приведите пример, как может выглядеть распределение этих данных. Как бы вы могли проверить, хотя бы графически, подтверждаются ли ваши ожидания?
Чтобы очистить, исследовать и представить данные, я бы провел EDA – Exploratory Data Analysis (разведочный анализ данных). В процессе EDA я бы построил гистограмму длительности звонков, чтобы увидеть их распределение.
Можно предположить, что длительность звонков следует логнормальному распределению. Длительность звонка не может быть отрицательной, так что нижнее значение равно 0. На другом конце гистограммы будет небольшое количество очень длинных звонков.
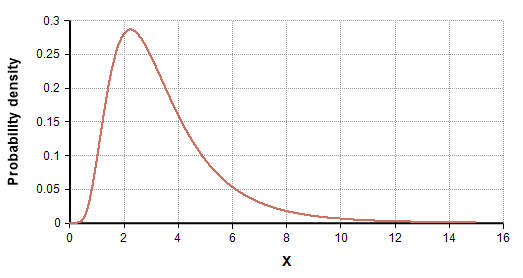
Чтобы подтвердить, распределена длительность звонков логнормально или нет, мы могли бы использовать график КК (QQPlot).
11. Расскажите, какой обычно бывает разница между административным набором данных и данными, полученными в результате эксперимента? Какие проблемы обычно встречаются в административных данных? Как экспериментальные данные позволяют справиться с этими проблемами, и какие проблемы они могут принести?
Административные наборы данных – это обычно наборы, используемые правительством или иными организациями для нужд, не связанных со статистикой.
Административные данные обычно больше, и их дешевле получить, чем экспериментальные данные. Вместе с тем, административные наборы данных часто не содержат всех данных, которые могут понадобиться, и могут храниться в неудобном формате. В них также встречаются ошибки и пропуски.
12. Вы составляете отчет по объему загруженного пользователями контента, и обнаруживаете пик загрузок в октябре – причем это пик загрузки изображений. Что могло послужить причиной этого, и как бы вы проверили свою догадку?
Есть несколько потенциальных причин пика загрузки изображений.
- В октябре могла появиться новая возможность, завоевавшая популярность пользователей. Например, возможность создания фотоальбомов.
- Возможно, до октября процесс загрузки изображений не был понятен пользователям, но именно в октябре это изменилось.
- В социальных сетях могло появиться вирусное движение, включающее загрузку фотографий, которое продолжалось весь октябрь.
- Возможно, люди публиковали свои фотографии в костюмах для Хэллоуина.
Метод проверки зависит от причины пика, но для тестирования правильности догадки используется проверка гипотез.
13. Вы летите в Казань, и хотите решить, стоит ли брать зонт. Вы звоните трем случайным казанцам и спрашиваете, идет ли дождь. Каждый из них говорит правду с вероятностью 2/3, а с вероятностью 1/3 обманывает вас. Все трое говорят, что дождь идет. Какова вероятность, что он идет на самом деле?
Поскольку последнее предложение фактически спрашивает: «какова вероятность A при условии, что верно B?», можно сразу сказать, что здесь нужна теорема Байеса. Нам потребуется информация о вероятности дождя в Казани в произвольный день, не связанный с полетом Допустим, она равна 25%.
P(A) = вероятность дождя = 25%
P(B) = вероятность, что все три казанца говорят, что идет дождь.
P(A|B) = вероятность дождя, при условии, что все трое говорят, что он идет.
P(B|A) = вероятность, что все трое говорят, что идет дождь, при условии, что он действительно идет = (2/3)3=8/27.
Шаг 1. Находим P(B)
Формулу Байеса P(A|B) = P(B|A) * P(A) / P(B) можно переписать в виде
P(B) = P(B|A) * P(A) + P(B| не А) * P(не A)
P(B) = (2/3)3*0.25 + (1/3)3*0.75 = 0.25*8/27 + 0.75*1/27.
Шаг 2. Находим P(A|B)
P(A|B) = 0.25*(8/27) / (0.25*8/27 + 0.75*1/27) = 8 / (8+3) = 8/11.
Таким образом, если все три казанца говорят, что идет дождь, то он действительно идет с вероятностью 8/11.
14. В первой коробке 12 черных и 12 красных карт, а во второй – 24 черных и 24 красных. Если вытянуть две случайные карты из одной коробки, для какой коробки вероятность вытянуть две карты одного цвета будет выше?
Вероятность вытянуть две карты одного цвета выше для второй коробки, содержащей по 24 карты каждого цвета.
Если мы вытянули, например, красную карту из первой коробки, там останется 11 красных карт и 12 черных, то есть вероятность вытянуть вторую красную карту будет 11 / (11+12) = 11/23.
Во второй коробке после вытягивания первой карты останется 23 карты того же цвета и 24 карты другого, то есть вероятность вытянуть вторую карту того же цвета будет 23 /(23+24) = 23/47.
Поскольку 23/47 > 11/23, вероятность вытянуть две карты одного цвета из коробки, в которой больше карт, выше.
15. Что такое подъем (lift), ключевые показатели эффективности (KPI), робастность, обучение модели, планирование эксперимента, правило 80/20?
Подъем (lift) – мера качества предсказаний модели по сравнению с моделью, выбирающей результат случайным образом. Иными словами, подъем определяет, насколько модель лучше, чем отсутствие какой-либо модели.
Ключевые показатели эффективности (KPI): измеримые метрики, показывающие, насколько хорошо компания добивается бизнес-целей. Например, это процент ошибок.
Под робастностью обычно понимают способность модели работать в сложных условиях (например, с данными, содержащими пропуски и выбросы), и оставаться эффективной.
Обучение модели – настройка внутренних параметров модели, чтобы добиться меньших ошибок на обучающем наборе данных.
Планирование эксперимента (design of experiment, DOE) – подготовка задач для описания и объяснения изменений информации, которые предположительно должны отражать поведение переменной. Фактически, эксперимент пытается предсказать результат, основываясь на изменении одного или более входных параметров – независимых переменных.
Правило 80/20 (закон Парето) гласит, что 80% эффекта получается от 20% случаев. Например, 80% продаж приходится на 20% клиентов.
16. Дайте определение понятиям «обеспечение качества» и «шесть сигм».
Обеспечение качества (Quality Assurance, QA) – действия или набор действий, направленных на поддержание желаемого уровня качества, минимизацию ошибок и дефектов.
Шесть сигм – вид методологии обеспечения качества, включающий набор техник и инструментов, улучшающих процесс. Процесс «шесть сигм» – тот, в котором 99.99966% результатов не имеют дефектов.
17. Приведите пример данных, распределение которых не Гауссово и не логнормальное.
- Любые категориальные данные не будут иметь ни гауссова, ни логнормального распределения.
- Экспоненциальные распределения. Например, количество времени, которое продержится автомобильный аккумулятор или время до следующего землетрясения.
18. Что такое RCA (root cause analysis)? Как отличить причину от корреляции? Приведите примеры.
Анализ причин (root cause analysis, RCA) – метод решения задач, используемый для выявления причин некоторого явления.
Корреляция измеряет уровень зависимости между двумя переменными, от -1 до 1. Причинно-следственная связь – это когда первое событие вызывает второе. Причинно-следственные связи учитывают только прямые зависимости, тогда как корреляция – и косвенные зависимости.
Провести анализ причинно-следственных связей можно с помощью проверки гипотез или A/B тестирования.
19. Приведите пример, когда медиана лучше описывает данные, чем среднее значение.
Когда в данных значительное количество выбросов в положительную или отрицательную сторону, медиана искажается не так сильно, как среднее значение.
20. Вы бросаете два шестигранных кубика. Какова вероятность, что сумма выпавших значений будет равна 4? А 8?
Выбросить 4 можно тремя комбинациями: (1+3, 2+2, 3+1). Поскольку всего комбинаций 36, P(4) = 3/36 = 1/12.
Выбросить 8 можно пятью комбинациями: (2+6, 3+5, 4+4, 5+3, 6+2). P(8) = 5/36.
21. Что такое Закон больших чисел?
Закон больших чисел – это теорема, согласно которой при увеличении количества испытаний среднее значение будет приближаться к ожидаемому.
Например, после 100 тыс. бросков правильной монеты процент выпавших гербов будет ближе к 50%, чем после 100 бросков.
22. Как рассчитать необходимый размер выборки?
Для определения желаемого размера выборки можно использовать формулу предельной ошибки (margin of error):
- t или z – значение t/z, использованное при расчете доверительного интервала.
- S - стандартное отклонение выборки.
23. Какие ошибки вы можете внести, когда делаете выборку?
- Ошибка выборки: неслучайный выбор включаемых в выборку объектов.
- Ошибка недостаточности: для анализа берется слишком мало наблюдений.
- Ошибка выжившего: игнорирование наблюдений, не прошедших через весь процесс получения данных.
24. Как уменьшить количество ошибок выборки?
Два простых метода – это рандомизация, при которой наблюдения выбираются случайным образом, и случайная выборка, при которой каждое наблюдение имеет равный шанс попасть в выборку.
25. Что такое вмешивающиеся переменные?
Вмешивающаяся переменная – это переменная, влияющая как на зависимую переменную, так и на независимую. Она создает мнимую ассоциацию – математическую связь, в которой задействовано несколько переменных, не имеющих причинно-следственных связей друг с другом.
26. Что такое A/B тестирование?
A/B тестирование – это метод проверки гипотез по двум выборкам для одной и той же переменной, контрольной и тестовой. Широко применяется для улучшения обслуживания пользователей и в маркетинге.
27. Уровень заражений в больнице, превышающий 1 заражение на 100 человеко-дней, считается высоким. В некоторой больнице было 10 заражений за последние 1787 человеко-дней. Вычислите P-значение верного одностороннего теста, чтобы определить, высок ли уровень заражений в этой больнице.
Поскольку мы анализируем количество событий (заражений), произошедших за определенный интервал времени, нужно использовать распределение Пуассона:
Нуль-гипотеза: 1 заражение на 100 человеко-дней или меньше
Альтернативная гипотеза: больше 1 заражения на 100 человеко-дней.
k (фактическое) = 10 заражений.
Лямбда (теоретическое) = 1/100 * 1787.
P = 0.032372 или 3.2372% (можно рассчитать с помощью using.poisson() в Excel, ppois в R или scipy.stats.poisson в Python)
Поскольку значение P меньше альфы (при уровне значимости 5%), мы отвергаем нулевую гипотезу, и делаем вывод, что больница не соответствует стандарту.
28. Вы бросаете несимметричную монету (вероятность герба=0.8) пять раз. Какова вероятность, что выпадет минимум три герба?
Для ответа на этот вопрос используем общую формулу биномиальной вероятности:
В нашей задаче p = 0.8, n=5, k=3, 4, 5.
P(3 или больше гербов) = P(3 герба) + P(4 герба) + P(5 гербов) = 0.94 или 94%.
29. Случайная величина X распределена нормально со средним значением 1020 и стандартным отклонением 50. Вычислите P(X>1200).
Используем Excel: p = 1-norm.dist(1200, 1020, 50, true). Получаем p=0.000159.
30. Пусть количество пассажиров на автобусной станции имеет распределение Пуассона со средним значением 2.5 в час. Какова вероятность, что за 4 часа появится не более трех человек?
x=3, а среднее значение за 4 часа = 2.5*4=10.
Используем Excel: p=poisson.dist(3, 10, true), и получаем p=0.010336.
31. Тест на ВИЧ имеет чувствительность 99.7% и специфичность 98.5%. Пациент из окружения с распространенностью заболевания 0.1% получил положительный результат теста. Какова точность теста (то есть, вероятность, что он ВИЧ-позитивен)?
Точность теста = PV+= (0.001*0.997)/[(0.001*0.997)+((1–0.001)*(1–0.985))] = 0.0624 или 6.24%.
Более подробно об этом уравнении можно прочитать здесь.
32. Вы баллотируетесь на пост, и ваш социолог опросил 100 избирателей, 60 из которых сказали, что собираются голосовать за вас. Можете ли вы быть уверены в победе?
- Примем для простоты, что у вас только один соперник.
- Также примем, что желаемый доверительный интервал составляет 95%. Это даст нам z-оценку 1.96.
В нашей задаче p = 0.6, z = 1.96, n = 100, что дает доверительный интервал [50.4, 69.6].
Таким образом, при доверительном интервале 95% вы можете расслабиться, только если ничего не имеете против победы с минимальным перевесом. В противном случае придется добиться 61 голоса из 100 опрошенных, чтобы не беспокоиться.
33. Счетчик Гейгера записывает 100 радиоактивных распадов за 5 минут. Найдите приблизительный 95% интервал для количества распадов в час.
- Поскольку это задача на распределение Пуассона, среднее = лямбда = дисперсия, что также означает, что стандартное отклонение = квадратному корню из среднего.
- Доверительный интервал 95% соответствует z-оценке 1.96.
- Одно стандартное отклонение = 10.
То есть, доверительный интервал равен 100 +/- 19.6 = [964.8, 1435.2].
34. Количество убийств в Шотландии упало со 115 до 99. Является ли это изменение значимым?
Эта задача аналогична предыдущей – зесь тоже используется распределение Пуассона. Доверительный интервал равен 115 +/- 21.45 = [93.55, 136.45]. Поскольку 99 находится в этом доверительном интервале, мы можем сделать вывод, что это изменение не является значимым.
35. Рассмотрим эпидемию инфлюэнцы для гетеросексуальных семей с двумя родителями. Предположим, что вероятность заражения хотя бы одного родителя 17%. Вероятность заражения отца 12%, а заражения обоих родителей – 6%. Какова вероятность заражения матери?
Используем общее правило сложения вероятностей:
P(мать или отец) = P(мать) + P(отец) – P(мать и отец)
P(мать) = P(мать или отец) + P(мать и отец) – P(отец) = 0.17 + 0.06 – 0.12 = 0.11
36. Предположим, что диастолическое кровяное давление мужчин от 35 до 44 распределено нормально со средним значением 80 (мм. рт. столба) и стандартным отклонением 10. Чему примерно равна вероятность того, что давление случайного мужчины меньше 70?
Поскольку 70 – это одно стандартное отклонение вниз от среднего значения, нужно взять площадь Гауссова распределения до минус одного стандартного отклонения: 2.3 + 13.6 = 15.9%.
37. Выборка 9 человек из интересующей нас популяции выявила средний объем мозга = 1100 куб.см. со стандартным отклоненим 30 куб.см. Каким будет 95% Т-доверительный интервал Стьюдента для среднего объема мозга в этой популяции?
Используем формулу доверительного интервала для выборки:
Учитывая уровень доверительности 95% и количество степеней свободы, равное 8, t-оценка = 2.306.
Доверительный интервал = 1100 +/- 2.306*(30/3) = [1076.94, 1123.06].
38. Девять испытуемых получали диетические пилюли на протяжении 6 недель. Средняя потеря веса составила -2 кг. Каким должно быть стандартное отклонение потери веса, чтобы верхняя граница 95% Т-доверительного интервала была равна 0?
Верхняя граница = среднее + t-оценка * (стандартное отклонение / квадратный корень из размера выборки).
0 = -2 + 2.306*(s/3)
2 = 2.306 * s / 3
s = 2.601903
Таким образом, стандартное отклонение должно быть примерно 2.60, чтобы Т-доверительный интервал заканчивался в нуле.
39. Для тестирования новой и старой систем сортировки пациентов неотложной помощи исследователи выбрали 20 ночей и случайным образом назначили новую систему сортировки на 10 из них, в остальных оставив старую. Они рассчитали среднее время ожидания (СВО) доктора для каждой ночи. Для новой системы СВО = 3 часа с отклонением 0.60, тогда как для старой было 5 часов с отклонением 0.68. Оцените 95% доверительный интервал для разницы в среднем СВО между системами. Считайте дисперсию постоянной.
Воспользуемся формулой нахождения доверительного интервала для двух независимых выборок (используем t-таблицу для n1+n2-2 степеней свободы):
Доверительный интервал – это среднее +/- t-оценка * стандартную ошибку.
Среднее значение = новое среднее – старое среднее = 3-5 = -2.
t-оценка равна 2.101, учитывая 18 степеней свободы (20-2) и 95% доверительный интервал.
Стандартная ошибка = sqrt(0.62*9+0.682*9)/(10+10–2)) * sqrt(1/10+1/10) = 0.352. Доверительный интервал = [-2.75, -1.25].
40. Для дальнейшего тестирования системы сортировки пациентов администраторы выбрали 200 ночей и случайным образом назначили новую систему на 100 из них, оставив старую для 100 остальных. Они посчитали среднее время ожидания (СВО) каждой ночи – для новой системы 4 часа со стандартным отклонением 0.5, а для старой – 6 часов со стандартным отклонением 2 часа. Рассмотрите гипотезу о сокращении времени ожидания при новой системе. Что предполагает 95% независимый групповой доверительный интервал с неравными дисперсиями для этой гипотезы? (Поскольку измерений на группу так много, просто используйте Z-квантиль вместо T).
Предположим мы вычитаем в порядке «Новая система – Старая система». Используем формулу доверительных интервалов для двух независимых выборок и Z-таблицу для стандартного нормального распределения:
среднее значение = новое среднее – старое среднее = 4-6 = -2
z-оценка = 1.96 для доверительного интервала 95%
Стандартная ошибка = sqrt((0.52*99+0.22*99)/(100+100–2)) * sqrt(1/100+1/100) = 0.205061.
Нижняя граница = -2–1.96*0.205061 = -2.40192
Верхняя граница = -2+1.96*0.205061 = -1.59808
Доверительный интервал равен [-2.40192, -1.59808]




Пишите в комментариях, если что-то нужно пояснить подробнее 👇🏻