Глазурь
Кондитер украшает огромный торт, покрывая прямоугольную поверхность разноцветной глазурью. Для приготовления глазури он смешивает сахарную пудру с лимонным и черничным соком в разных пропорциях, чтобы получить три оттенка синего цвета: светлый, средний и насыщенный. Эти цвета обозначаются числами: 0 для светлого, 1 для среднего и 2 для насыщенного синего.
Чтобы получить красивый узор, он разделяет поверхность торта на вертикальные полосы шириной A1, A2, ..., An сантиметров и горизонтальные полосы высоты B1, B2, ..., Bn сантиметров. В результате полосы делят поверхность торта на n × n прямоугольников. Пересечение вертикальной полосы i и горизонтальной полосы j имеет цветовой номер (i + j) mod 3 для всех 1 ≤ i, j ≤ n:
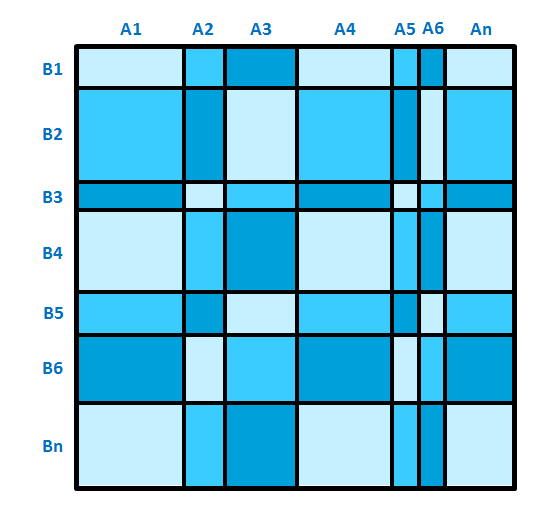
Помогите кондитеру определить площадь каждого из трех цветов в квадратных сантиметрах. Программа получает на вход целое положительное число n, и две строки, в которых перечисляется ширина и высота полос.
Пример ввода
7
6 2 4 5 1 1 4
2 5 1 4 2 3 4
Вывод
155 131 197
Решение
Наша цель – найти решение, которое работает за время O(n) или O(n log n) в худшем случае. Первое, что приходит в голову – перебрать все ячейки сетки n x n и посчитать площадь каждого цвета отдельно. Однако это решение займет слишком много времени, так как количество операций растет пропорционально квадрату n.
Более оптимальный подход
Если мы поменяем столбцы или строки местами, то общая площадь каждого цвета останется прежней. Например, если мы переместим столбец целиком, то темно-синие ячейки просто переместятся вместе со столбцом, не изменяя их общей площади.
Следовательно, достаточно рассмотреть случай n = 3. Тогда мы можем просто посчитать площади каждого цвета, суммируя ячейки с одинаковым остатком от деления суммы индексов строки i и столбца j на 3. Например:
- A3k (светло-синий): сумма площадей ячеек, где (i + j) дает остаток 0 при делении на 3
- A3k+1 (средний синий): сумма площадей ячеек, где (i + j) дает остаток 1 при делении на 3
- A3k+2 (насыщенный синий): сумма площадей ячеек, где (i + j) дает остаток 2 при делении на 3
Таким образом, мы можем найти площадь каждого цвета, просмотрев только сетку 3 x 3. Единственная сложность – нужно правильно учитывать цвета при суммировании площадей:
def read_ints():
return list(map(int, input().split()))
def cat(l):
return tuple(sum(l[n::3]) for n in [1, 2, 0])
input()
A = cat(read_ints())
B = cat(read_ints())
print(
f"{B[2] * A[0] + B[0] * A[2] + B[1] * A[1]} "
f"{B[2] * A[1] + B[0] * A[0] + B[1] * A[2]} "
f"{B[2] * A[2] + B[0] * A[1] + B[1] * A[0]}"
)
Учитесь программировать на Python в удобном темпе!
Вы хотите начать карьеру в IT или повысить свои навыки программирования? Наш курс идеально подходит как для новичков, так и для начинающих разработчиков!
💡 Что вас ждет на курсе
- 32 урока практических занятий.
- 4 проекта для личного портфолио: бот для Telegram, парсинг веб-страниц, генератор безопасных паролей, калькулятор для ипотеки.
- 90 часов практики и 15 часов теории.
- Работа в PyCharm и Jupyter Notebook.
- Обратная связь от опытных преподавателей.
👨🏫 Преподаватели
- Роман Булгаков — эксперт с 5-летним стажем, готовит школьников и студентов к олимпиадам по информатике.
- Артур Сапрыкин — Ex-Data Scientist ПАО «Мегафон», работал с крупными проектами по обработке естественного языка и анализом аудио.
📅 Начало курса в любое время! Учитесь в удобном для вас темпе на платформе CoreApp.
Вид на море
При застройке набережной строительная компания расположила здания в неправильном порядке. В результате многие дома не имеют вида на море:
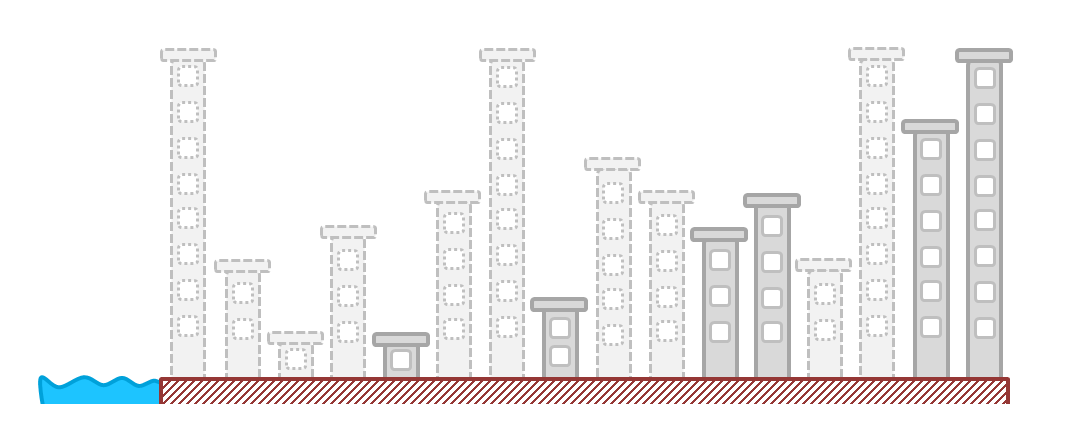
Власти города решили снести все здания, перекрывающие вид на море. Напишите программу, которая получает на вход список, в котором перечисляется количество этажей каждого здания, и возвращает список зданий, которые останутся после сноса.
Пример ввода
7 1 4 3 5 9 3
Вывод
1 3 5 9
Решение
Задача сводится к поиску наибольшей увеличивающейся подпоследовательности. Сложность этого алгоритма составляет O(n log m), где n – размер входного массива x, а m – размер самой длинной возрастающей подпоследовательности.
Основные идеи решения:
- Для каждого индекса i мы добавляем элемент x_i к самой длинной возрастающей подпоследовательности, которая строится на основе префикса x_1, ..., x_{i-1}.
- Чтобы найти оптимальное решение, мы будем рассматривать множество всех возможных подпоследовательностей префикса x_1, ..., x_{i-1}. Две важных характеристики каждой подпоследовательности y – это ее длина и последний элемент.
- Мы будем хранить только недоминируемые подпоследовательности, то есть те, которые не меньше по длине и не больше по последнему элементу, чем другие подпоследовательности той же длины. Это позволит нам избежать хранения избыточной информации.
- Для эффективного хранения недоминируемых подпоследовательностей мы будем использовать массив b, где b[k] – последний элемент самой длинной подпоследовательности длины k. Этот массив будет строго возрастающим.
- Когда мы рассматриваем очередной элемент x_i, то ищем, в какую из недоминируемых подпоследовательностей можно добавить x_i, чтобы получить новую, более длинную подпоследовательность. Это можно сделать за O(log m) с помощью бинарного поиска.
- Для хранения самих подпоследовательностей мы используем связанные списки, представленные с помощью двух массивов: h (хранит индексы элементов в x) и p (хранит индексы предыдущих элементов в списке).
from bisect import bisect_left
def demolish(x):
n = len(x)
p = [None] * n # Индексы предыдущих элементов
h = [None] # Индексы элементов, образующих возрастающую подпоследовательность
b = [float('-inf')] # Значения элементов, образующих возрастающую подпоследовательность
for i in range(n):
if x[i] > b[-1]: # Если текущий элемент больше последнего в b, добавляем его в конец
p[i] = h[-1]
h.append(i)
b.append(x[i])
else: # В противном случае используем бинарный поиск для нахождения позиции вставки
k = bisect_left(b, x[i])
h[k] = i
b[k] = x[i]
p[i] = h[k - 1]
# Извлекаем решение в обратном порядке
q = h[-1]
s = []
while q is not None:
s.append(x[q])
q = p[q]
return s[::-1] # Возвращаем решение в прямом порядке
arr = list(map(int, input().split()))
print(*demolish(arr))
Цукаты
Вася очень любит цукаты, но терпеть не может пироги. Однако цукаты можно получить только вместе с куском пирога, который они украшают. Какой наименьший кусок пирога должен отрезать Вася, чтобы получить хотя бы одному из всех видов цукатов?
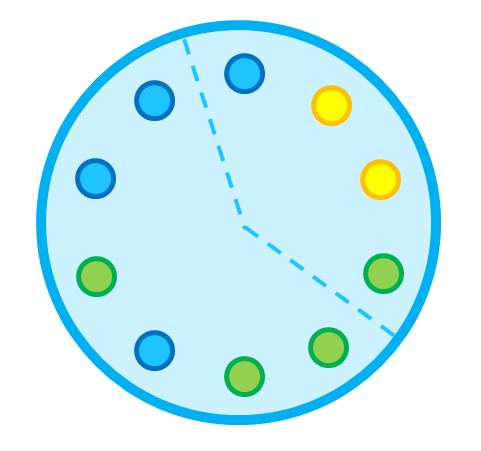
Цукаты обозначаются буквами английского алфавита. Программа сначала получает строку с буквами, а затем целое число – нужное количество разновидностей цукатов.
Пример ввода
a b b c c c a c a a
3
Вывод
(0, 4)
Решение
Это вариант популярной на собеседованиях задачи по подсчету элементов в каждом окне размера k. В нашем случае решение должно определять диапазон куска, в который входит хотя бы один экземпляр из заданного количества видов цукатов. Решение имеет временную сложность O(n), где n – длина входной строки, так как оно проходит по строке один раз, используя скользящее окно:
def window(x, k):
n = len(x)
i = j = 0
freq = [0] * 26
distinct = 0
min_len = float('inf')
min_window = None
while j < n:
if distinct < k:
if freq[ord(x[j]) - ord('a')] == 0:
distinct += 1
freq[ord(x[j]) - ord('a')] += 1
j += 1
while distinct == k and i < n:
if j - i < min_len:
min_len = j - i
min_window = (i, j)
freq[ord(x[i]) - ord('a')] -= 1
if freq[ord(x[i]) - ord('a')] == 0:
distinct -= 1
i += 1
return min_window if min_window else None
x = input().split()
k = int(input())
print(window(x, k))
Спутниковые антенны
Бесконечная береговая линия определяется как ось x. Море находится выше оси x, а суша – ниже. В море расположены небольшие острова, которые можно считать точками с координатами x и y. Зеленые спутниковые антенны, расположенные на берегу, могут покрывать дистанцию d. Необходимо написать программу, которая в первой строке получает дистанцию d и число островов n, а во второй – n наборов координат островов, и определяет минимальное необходимое количество антенн для покрытия всех островов:
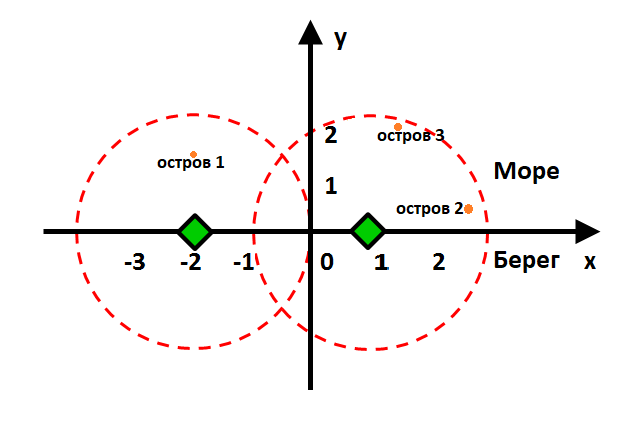
Пример ввода
3 2
1 2
-3 1
2 1
Вывод
2
Решение
Воспользуемся подходом, который лежит в основе алгоритма заметающей прямой. Основная идея состоит в том, чтобы проходить линию от левого края до правого по плоскости, обрабатывая события, которые происходят при пересечении этой линии с объектами на плоскости. Сложность решения составляет O(n log n):
def installations(islands, d):
# Сортируем острова по координате x
islands.sort(key=lambda x: x[0])
# Список для хранения самой правой координаты x, покрытой каждой антенной
sats = []
for x, y in islands:
# Если остров не покрыт последней антенной, размещаем новую
if not sats or sats[-1] < x:
sats.append(x + d) # Размещаем антенну на координате x острова + расстояние покрытия
else:
# Обновляем самую правую координату x, покрытую последней антенной
sats[-1] = max(sats[-1], x + d)
# Количество антенн равно длине списка sats
return len(sats)
n, d = [int(_) for _ in input().split()]
islands = [list(map(int, input().split())) for _ in range(n)]
print(installations(islands, d))
Самый длинный палиндром
Напишите программу, которая получает на вход строку, содержащую один или более палиндромов, и определяющую самый длинный из них. Если в строке содержатся несколько палиндромов одинаковой длины – вывести любой из них. Пробелов и знаков препинания в строке нет.
Пример ввода
аннаахматовалешанаполкеклопанашел
Вывод
лешанаполкеклопанашел
Решение
Эту задачу можно решить за квадратичное время с наивным алгоритмом и за O(n log n) с помощью массивов суффиксов. Более эффективный подход предлагает алгоритм Манакера, разработанный в 1975 году.
Ключевая идея алгоритма – использовать симметрию палиндромов, чтобы эффективно вычислять длины максимальных палиндромов, центрированных на каждом символе входной строки.
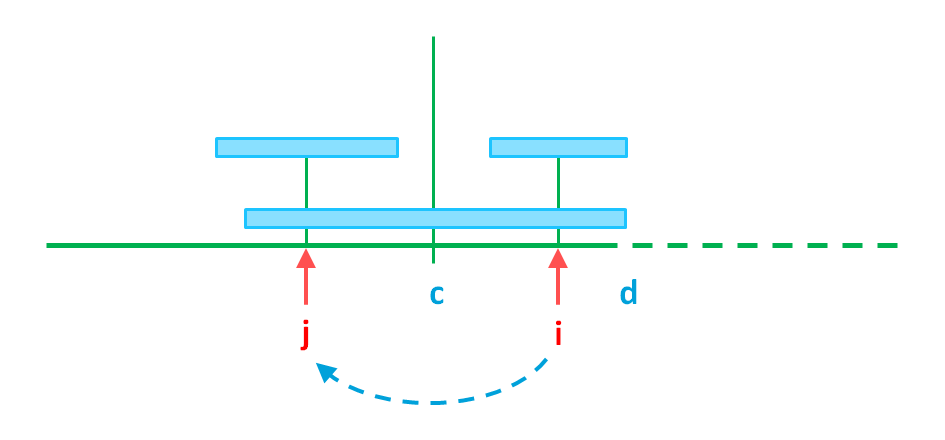
Предположим, что есть палиндром, центрированный на c, радиуса d – c, где d – максимальный такой индекс. Пусть j – зеркальное отражение i относительно c.
Из симметрии следует, что палиндром, центрированный на j, радиуса p[j], должен быть равен слову, центрированному на i, по крайней мере, до радиуса d – i. Следовательно, p[j] является нижней границей для значения p[i].
Это значит, что мы можем начать вычисление p[i] с p[j] и двигаться вправо, сравнивая символы, пока они совпадают. Это позволяет вычислить p[i] за линейное время, так как мы используем информацию, полученную при вычислении предыдущих значений p:
Основные этапы решения:
- Преобразуем входную строку s, вставляя разделитель # вокруг каждого символа и добавляя ограничители ^ и $ по краям строки. Например, abc преобразуется в ^#a#b#c#$. Пусть полученная строка называется t.
- Это позволяет обрабатывать одинаковым образом палиндромы как четной, так и нечетной длины.
- Заметим, что при этом преобразовании каждый палиндром начинается и заканчивается с разделителя #. Таким образом, два конца палиндрома имеют индексы с одной и той же четностью, что упрощает преобразование решения для строки t в решение для исходной строки s.
- Ограничители ^ и $ избавляют от необходимости рассматривать граничные случаи.
def manacher(s):
# Преобразуем исходную строку s в строку t
# с добавлением разделителей # и ограничителей ^ и $
t = "^#" + "#".join(s) + "#$"
n = len(t)
# Массив p, где p[i] будет хранить
# длину максимального палиндрома, центрированного в i-м символе
p = [0] * n
# center - индекс центра последнего найденного палиндрома
# right - индекс правой границы последнего найденного палиндрома
center = right = 0
# Вычислим длины максимальных палиндромов
for i in range(1, n - 1):
# Если i находится внутри последнего найденного палиндрома,
# то можем использовать симметрию для нахождения p[i]
if i <= right:
mirror = 2 * center - i
p[i] = min(right - i, p[mirror])
# Расширяем палиндром, центрированный в i-м символе
while t[i + p[i] + 1] == t[i - p[i] - 1]:
p[i] += 1
# Обновляем center и right, если необходимо
if i + p[i] > right:
center = i
right = i + p[i]
# Находим самый длинный палиндром
max_len, max_center = max((p[i], i) for i in range(1, n - 1))
start = (max_center - max_len) // 2
end = start + max_len
# Возвращаем границы самого длинного палиндрома в исходной строке s
return start, end
s = input()
result = manacher(s)
print(s[result[0]:result[1]])
Другие задачи
Решаем 5 олимпиадных задач на Python: используем битовую маску для выбора симпатичных узоров, находим оптимальную стратегию игры, подсчитываем варианты вырубки деревьев, и выясняем, за сколько секунд можно пробежать по эскалатору.
Подготовка к собеседованию по Python: составляем анонимку, проверяем гипотезу Коллатца, решаем судоку, разрабатываем кэш для операций над ISBN и вычисляем интервалы занятости.
Решаем 5 интересных задач: проверяем двоичные деревья на симметричность, вычисляем расстояние Дамерау-Левенштейна и оцениваем сложность алгоритмов.



Комментарии