В начале 17 века математик и астроном по имени Эдмунд Гантер столкнулся с исключительной астрономической задачей. Вычисление движения планет и предсказание затмений требовали больше чем просто интуиции — были необходимы знания сложных логарифмических и тригонометрических уравнений. Поэтому, как и любой другой опытный изобретатель, Гантер решил построить их с нуля! Он создал аналоговое вычислительное устройство, которое впоследствии стало известно как логарифмическая линейка.
Будучи прямоугольным деревянным блоком длиной в 30 сантиметров, логарифмическая линейка состоит из двух частей: фиксированной рамы и подвижной части. На раме есть неподвижные логарифмические шкалы и подвижная шкала. Чтобы использовать такую линейку, нужно понимать базовые принципы логарифмов и как сопоставить шкалы для умножения, деления и других математических операций. Надо было сдвинуть подвижную часть для сопоставления чисел, прочесть результат и учесть расположение десятичной точки.

Примерно через 300 лет, в 1961 году, Bell Punch Company представила первый настольный калькулятор, ANITA Mk VII. В течение следующей пары десятилетий электронные калькуляторы стали более сложными. Задачи, ранее требовавшие длинных вычислений, претерпели заметное снижение необходимого на их выполнение рабочего времени, что позволило работникам сфокусироваться на более аналитических и креативных аспектах их работы. В результате современный электронный калькулятор не только изменил рабочие роли, но также проложил дорогу для больших возможностей решения различных задач.
Калькулятор стал прорывом в выполнении математических операций. Что насчёт языка?
Подумайте о том, как вы составляете предложения. Для начала необходима идея. Затем надо знать какие-то слова (словарный запас). Потом стоит уметь соединять их в правильные предложения (грамматика).

Мы довольно последовательно производили слова 50 000 лет назад, как раз, когда современный человек впервые придумал язык.
Справедливо будет сказать, что когда речь идёт о формировании предложений, мы всё ещё находимся в Гюнтеровской эре использования логарифмической линейки!
Если задуматься, использование подходящих лексикона и грамматики — это просто следование правилам. Правилам языка.
Это похоже на математику. Она полна правил. Вот почему я могу быть уверен в том, что 1+1=2, и в том, как работают калькуляторы!
Что нам нужно, так это калькулятор, но для слов!
Да, разные языки следуют разным правилам, но эти правила должны выполняться, чтобы языки были понятны. Очевидная разница между языками и математикой состоит в том, что в математике есть однозначные ответы, в то время как количество подходящих слов, которые можно вставить в предложение, может быть огромным.
Попробуйте закончить предложение: Я съел _________. Представьте возможные слова, которыми можно его продолжить. В английском примерно 1 миллион слов. Многие из них можно использовать здесь, но точно не все.
Ответ «чёрную дыру» будет эквивалентом заявления, что 2+2=5. Ответ «яблока» также будет неверным. Почему? Из-за грамматики!

В последние месяцы Большие Языковые Модели (LLM) захватили мир. Некоторые называют их прорывом в обработке естественного языка, а другие видят в них начало новой эры искусственного интеллекта (ИИ).
LLM оказались особенно хороши в образовании текста похожего на человеческий, поднимая планку для языковых приложений с ИИ. С учётом широкой базы знаний и контекстуального понимания LLM можно применять в различных сферах начиная от переводов и генерации контента и заканчивая виртуальными помощниками и чатботами поддержки клиентов.
Вопрос: настал ли такой же переломный момент с LLM, какой был в 1960-х с электронным калькулятором?
Прежде чем ответить на это, разберём, как работают LLM. Они основаны на трансформерах, которые используются для вычисления и определения, какие слова лучше всего подойдут предложению. Чтобы построить мощную нейронную сеть-трансформер, необходимо обучить её на огромном количестве текстовых данных. Вот почему подход «предположить следующее слово/токен» так хорошо работает: обучающие данные легко достать. На вход LLM берёт всю цепочку слов и определяет, какое слово с наибольшей вероятностью будет дальше. Чтобы изучить, что скорее всего будет дальше, LLM прочёсывают всю Википедию в качестве разминки, прежде чем перейти на книги, а потом и весь интернет.
Ранее мы установили, что язык содержит правила и паттерны. Модель косвенно учит эти правила, перебирая все эти предложения, чтобы спрогнозировать следующее слово.
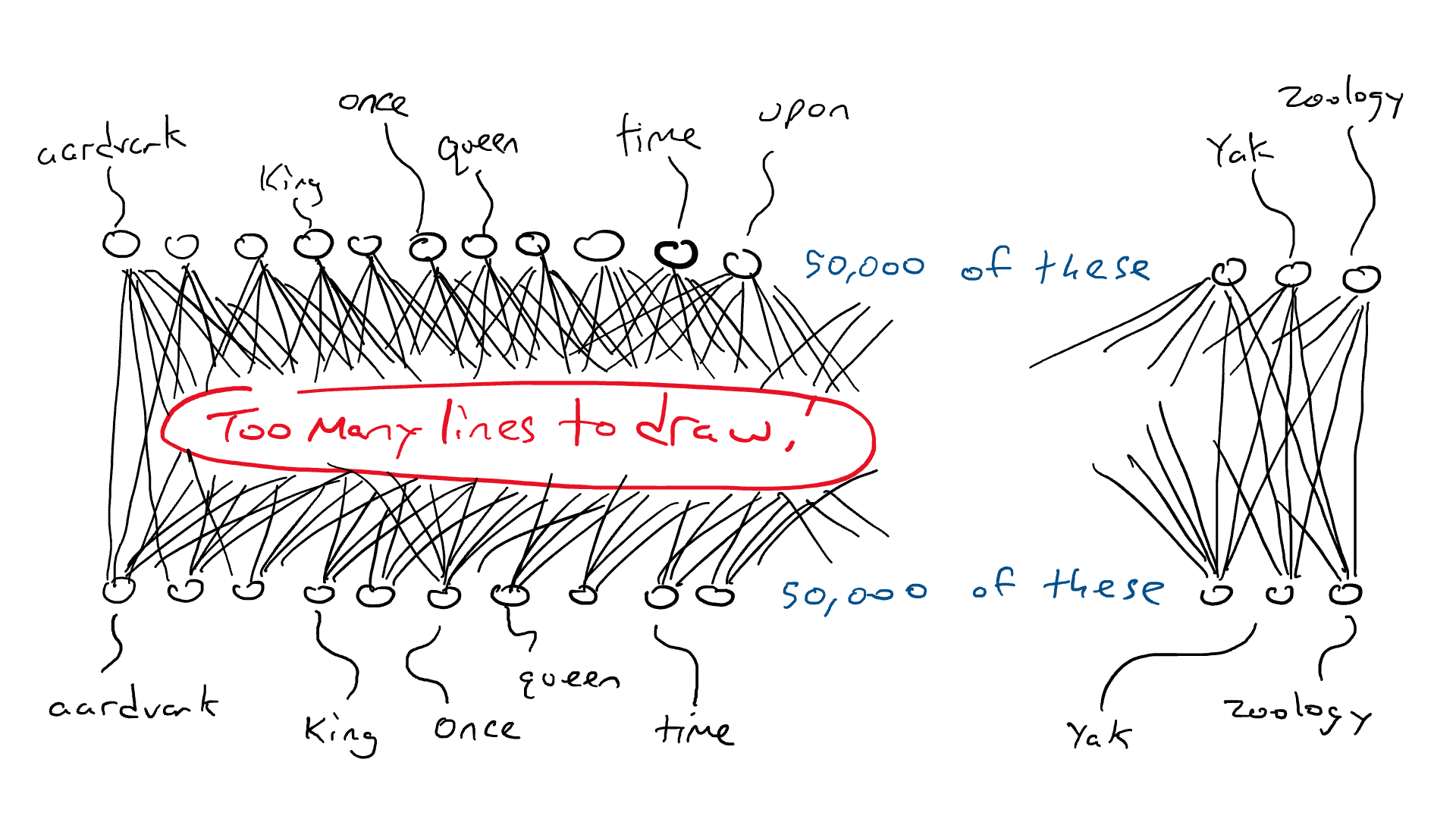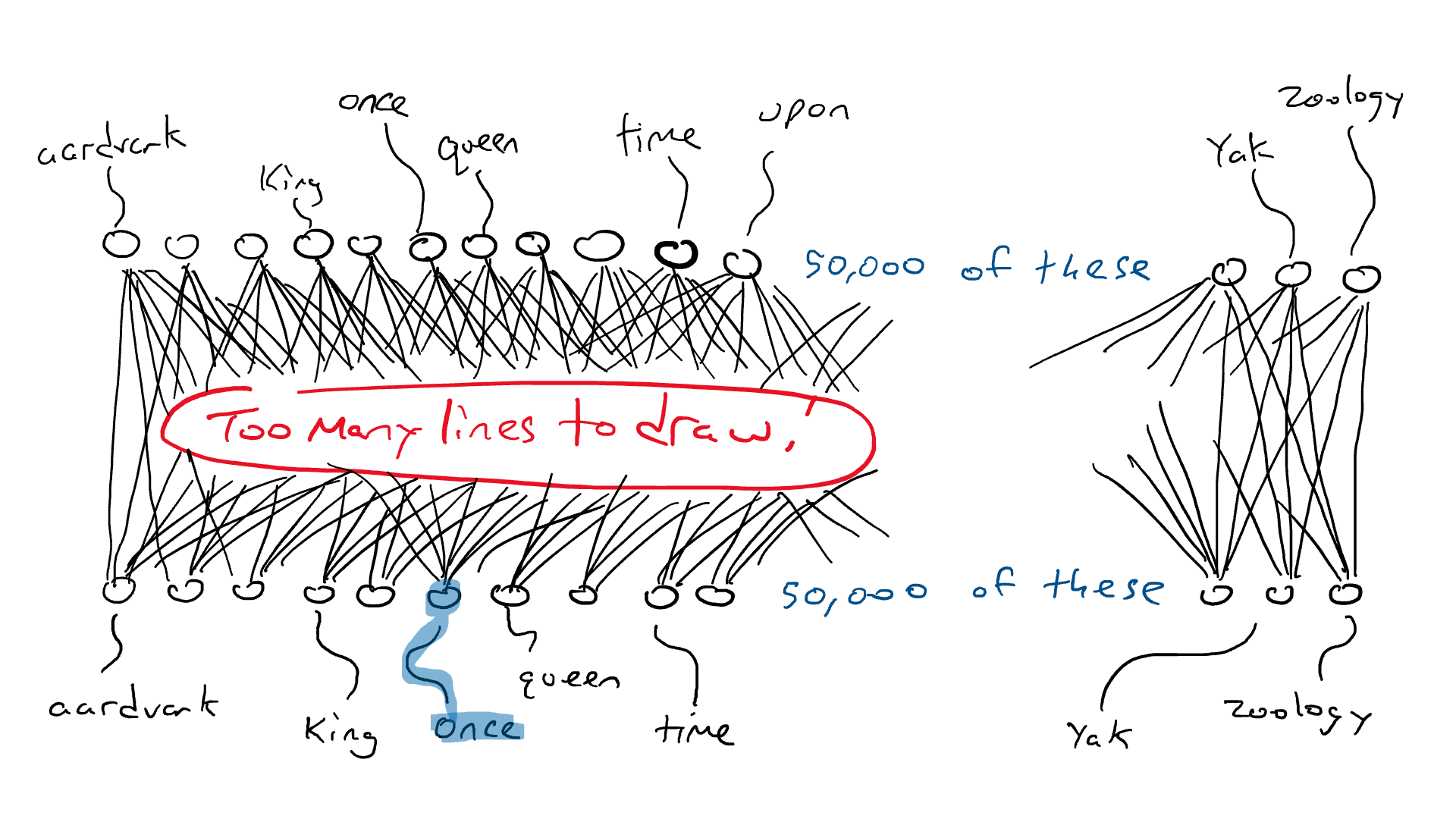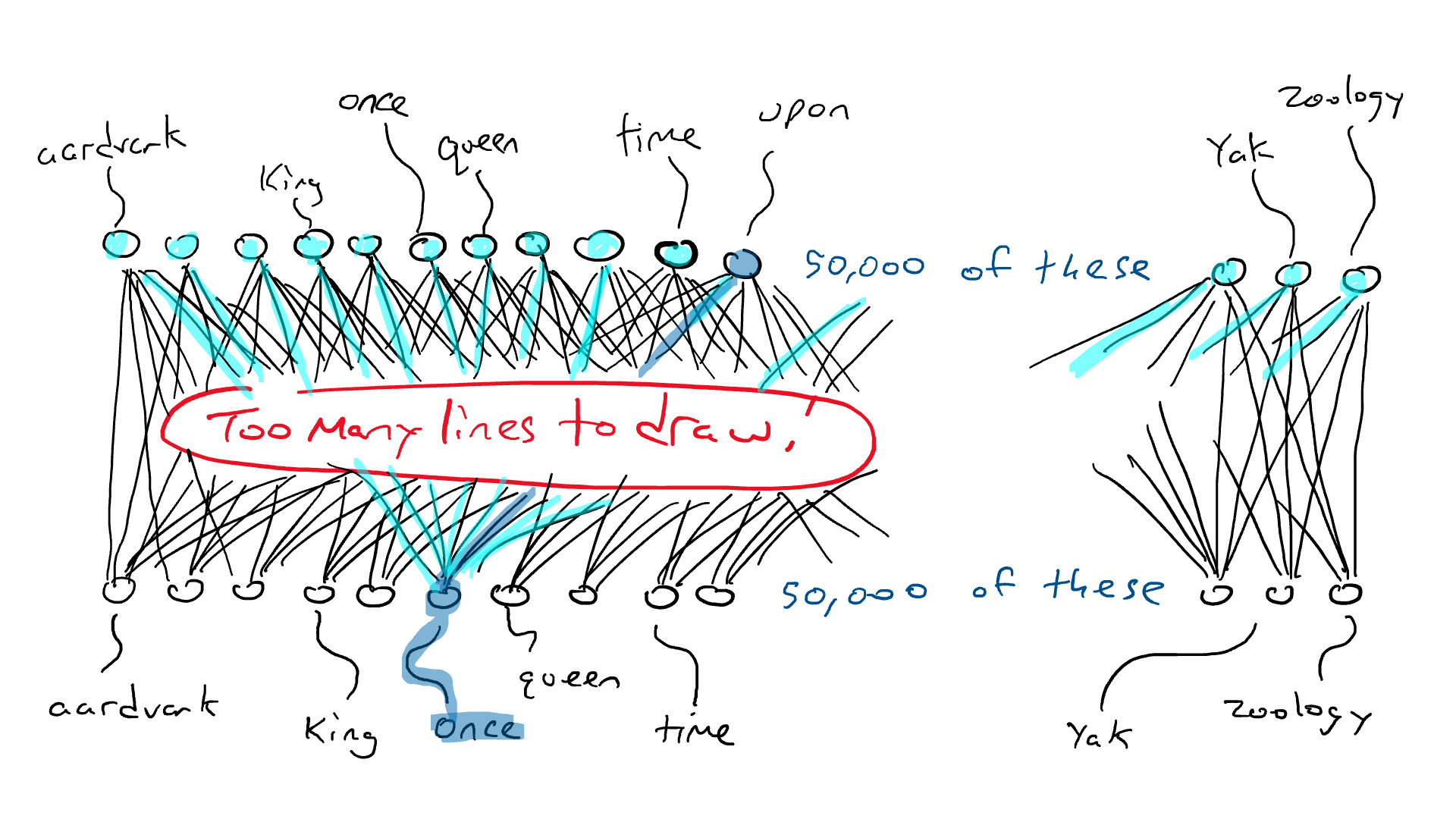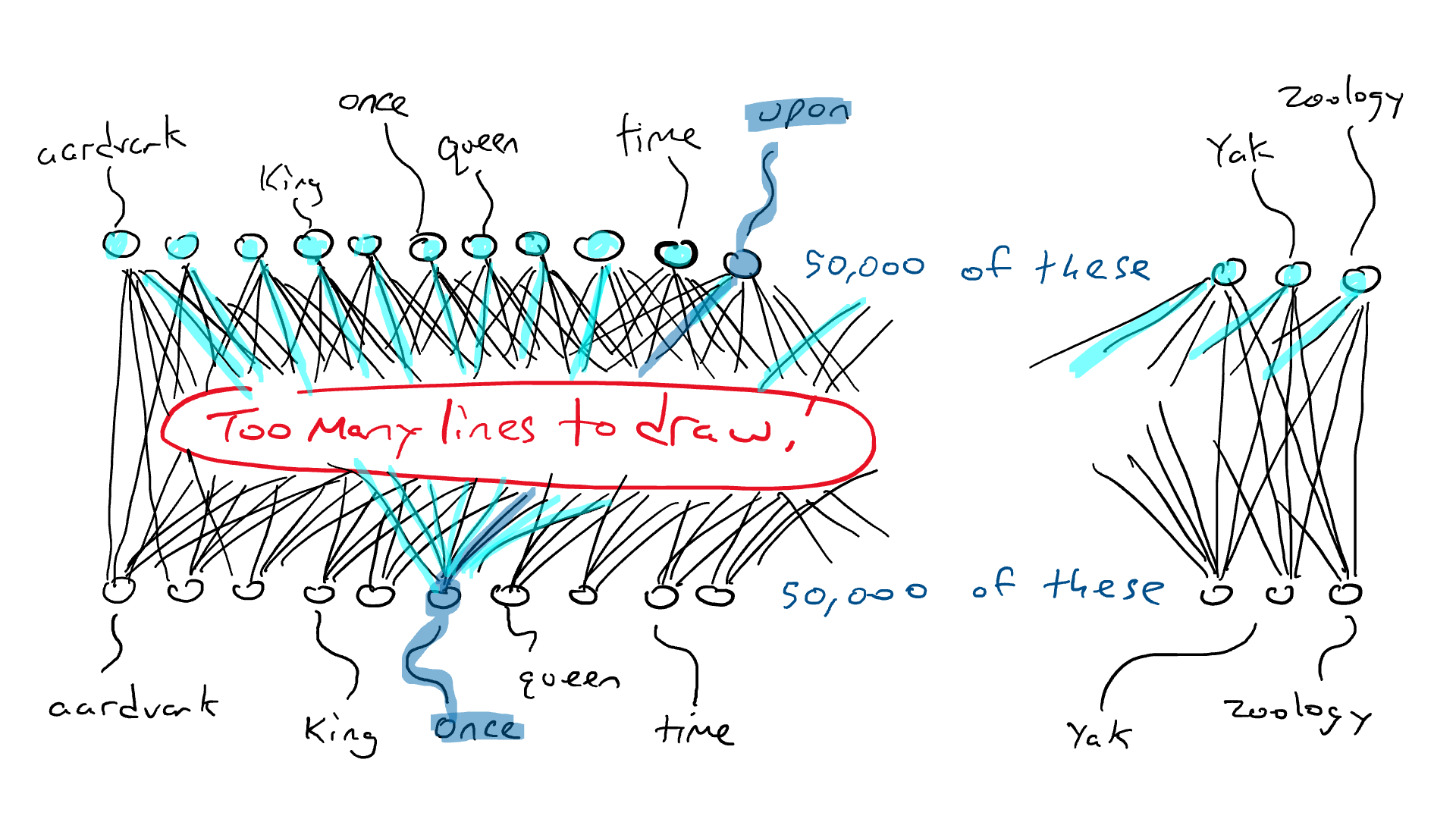
После существительного во множественном числе с большой вероятностью последует глагол с окончанием «и». В том же духе, при чтении Шекспира повышаются шансы увидеть слова по типу «дабы» и «посему».
Во время обучения модель учит эти языковые паттерны, постепенно становясь экспертом!
Но достаточно ли этого? Достаточно ли изучения языковых правил?

Язык запутан — одно слово принимает множество значений в зависимости от контекста.
Поэтому — механизм самовнимания. Простыми словами, самовнимание — это техника, которая используется LLM для понимания закономерностей между различными словами в предложении или тексте. Как мы обращаем внимание на разные части истории, чтобы понять её, так и самовнимание позволяет LLM придать большее значение определённым словам в процессе обработки информации. Так модель лучше понимает общий смысл и контекст текста, а не вслепую предугадывает слово на основании лишь языковых правил.

Если LLM — это калькуляторы слов, просто предугадывающие следующее слово, то как они отвечают на все мои вопросы?
Когда вы просите Большую Языковую Модель сделать что-то умное, и она работает, то высока вероятность того, что она уже видела тысячи примеров выполнения этого задания. И даже если вы придумаете что-либо уникальное, например:
«Напиши мне стихотворение о том, как косатка ест курицу»
Amidst the waves, a sight unseen, An orca hunts, swift and keen, In ocean’s realm, the dance begins, As a chicken’s fate, the orca wins. With mighty jaws, it strikes the prey, Feathers float, adrift away, In nature’s way, a tale is spun, Where life and death become as one.
Довольно неплохо, да? Благодаря своему механизму самовнимания, модель может успешно смешать и сопоставить подходящую информацию, чтобы создать правдоподобный и связный ответ.
Во время процесса обучения LLM учатся распознавать паттерны, ассоциации и отношения между словами и фразами. В результате этого экстенсивного обучения и регуляции LLM могут показывать эмердживные свойства, такие как умение переводить тексты, реферировать, отвечать на вопросы и даже практиковать креативное письмо. Эти умения выходят за рамки того, что было явно запрограммировано в модель.
Большие Языковые Модели разумны?
Электронный калькулятор существует уже более шести десятилетий. Сам инструмент развивался семимильными шагами, но никогда не считался разумным. Почему?
Калькулятор никогда не подвергался тесту Тьюринга, потому что он общается не тем же языком, что и люди, а только языком математики. С другой стороны, LLM генерируют человеческий язык. Весь их процесс обучения завязан на подражании ему. Поэтому не удивительно, что они могут «вступить в диалог с человеком и быть от него неотличимыми».
Сложно сказать, что LLM «разумны», потому что нет точной договорённости о значении разума. Определить, разумно ли что-либо, можно по тому, делает ли это что-то интересные, полезные и не очень очевидные вещи. LLM входят в эту категорию. Тем не менее я полностью несогласен с этой точкой зрения.
Я определяю разумность как способность расширить границы знаний.
На момент написания данной статьи машина, обученная определять следующие токены/слова, всё ещё не способна расширить эти границы.
Что она может, так это интерполировать на основе тренировочных данных. Нет явного понимания логики, как нет и дерева знаний. Как следствие, такая машина никогда не сможет придумать выдающиеся идеи или испытать момент прозрения. Она всегда будет давать точные, но довольно обычные ответы.

Так что это значит для людей?
Мы должны относиться к LLM скорее как к калькулятору для слов. Никогда не делегируйте всё своё мышление языковой модели.
В то же время, так как эти модели становятся всё лучше, можно начать чувствовать себя всё более подавленными и незначительными. Решением такой проблемы является постоянный интерес к идеям по виду не связанным между собой. Идеям, которые на первый взгляд кажутся бессвязными, но начинают иметь смысл с учётом нашего взаимодействия с окружающим миром. Надо жить на краю знаний, создавая и сопоставляя новые факты.
При таком раскладе все виды технологий, будь то калькулятор или большая языковая модель, станут инструментами, а не экзистенциальной угрозой.





Комментарии