Что такое дифференцируемость?
Однажды восприняв теорию эволюции, вы начинаете видеть природу с позиций конкуренции и выживания. Вы понимаете, почему микробы становятся резистентными к лекарственным препаратам (выживание наиболее приспособленных). Или, например, почему нас тянет к сладкой и жирной пище (поощрение природой потребления высококалорийных продуктов на случай дефицита).
Аналогичным образом изучение математического анализа подобно просветлению. В школьном курсе мы изучаем приведенные ниже формулы в различных разделах геометрии, получаем их как данность. Но разве они не связаны каким-то образом? Математический анализ показывает, что одно следует из другого. Сегодня мы будем двигаться относительно приведенного изображения справа налево. Как бы расщепляя природу объектов, подменяя их более простыми сущностями, дифференцируя.
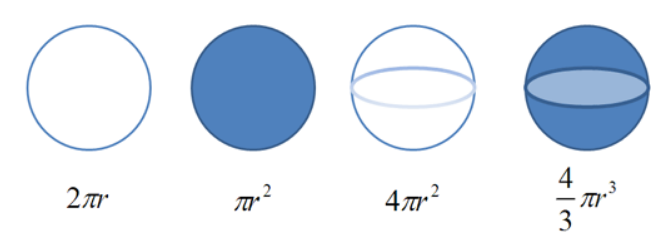
Понятие «дифференцируемость» лежит в основании математического анализа. Изначально этот курс так и назывался: интегральное и дифференциальное исчисление. Что подразумевают математики, когда говорят, что функция дифференцируема в точке?
В учебниках по математическому анализу даётся следующее определение (не пугайтесь, далее мы будем излагать мысли более простым языком). Функция f дифференцируема в точке x, если её приращение в этой точке представимо в виде:
Здесь A – постоянная, не зависящая от приращения аргумента Δx. Обозначение
соответствует бесконечно малой функция более высокого порядка, чем Δx.
Далее в учебниках доказывается, что для дифференцируемости функции f в точке x необходимо и достаточно существование в этой точке предела.
который называется производной функции f в точке x .
Потом обычно устанавливаются правила дифференцирования, арифметические свойства, доказываются основные теоремы дифференциального исчисления и т.п.
Однако за этим нагромождением нередко пропадает основная идея понятия дифференцируемости. Если функция y = f(x) дифференцируема в точке x и вычислимо значение f(x+ Δx), то ее можно представить в виде линейной функции y = AΔx + B, с "хорошей степенью точности".
Перейдем к примерам
Рассмотрим примеры различных функций. Исходя из обозначенной главной идеи, будем задаваться при рассмотрении каждой зависимости вопросом: можно ли представить исследуемую функцию f(x) в виде прямой линии вблизи точек x? Обсудим, что именно мы под этим подразумеваем, на ряде конкретных примеров.
Синусоидальная функция
Начнем с простой степенной функции – синусоидальная функция f(x) = sin*x.
Здесь и далее на анимациях сверху изображается график исследуемой функции на заданном отрезке (сплошная линия), а также хорда (оранжевый пунктир), соединяющая точки зависимости, соответствующие концам выбранного числового отрезка.
Одновременно снизу строится функция модуля разности между исходной функцией и описывающей хорду линейной зависимостью.
Синусоидальная функция дифференцируема на всей числовой прямой. На gif-изображении ниже можно видеть, что после нескольких приближений к точке x=0 график функции сливается с хордой, превращаясь в прямую линию. Соответствующая разность с каждой итерацией на всем выбранном отрезке становится все ближе к нулю. Эта ситуация соответствует устремлению приращения к нулю.
Модуль гармонической функции
Существует бесконечное число примеров, когда подобного приближения указанной разности к нулю представить нельзя. То есть нельзя говорить и о дифференцируемости функции.
Возьмем, например, функцию модуля гармонической функции f(x) = |sinx|. Легко доказать, что эта функция не дифференцируема во всех точках, в которых значение синуса обращается в ноль.
Пусть x = 0. На анимации ниже заметно, что какой бы малый отрезок вокруг этой точки мы ни брали, рассматриваемая разность не устремляется к нулю.
Композиции степенных и гармонических функций
Указанный подход позволяет визуализировать и более сложные примеры композиций нескольких функций.
Рассмотрим две родственные функции:
и
Первая функция дифференцируема при x=0, вторая – нет. Это хорошо видно на анимациях ниже.
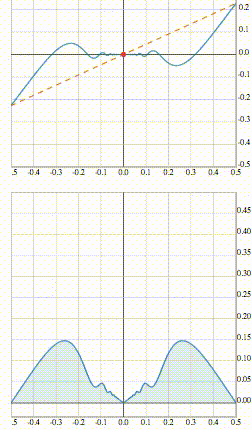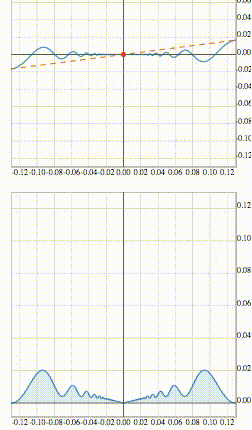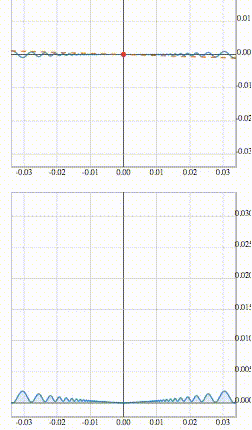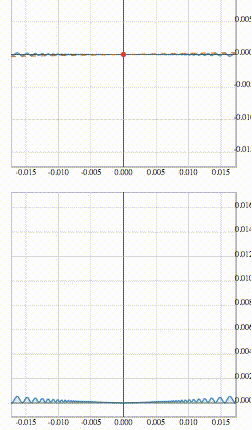
Обсудим теперь поведение подобных функций с немного другой точки зрения. Для этого рассмотрим функцию
, домноженную на степенные функции с различным показателем.
Простейший вариант –
Эта функция имеет разрыв в x=0. Проиллюстрируем ситуацию точкой, движущейся по графику данной функции.
При приближении к началу координат рассматриваемая точка начинает скакать и дёргаться, то есть не стремится к какому-то определенному значению. Функция
терпит в x=0 разрыв.
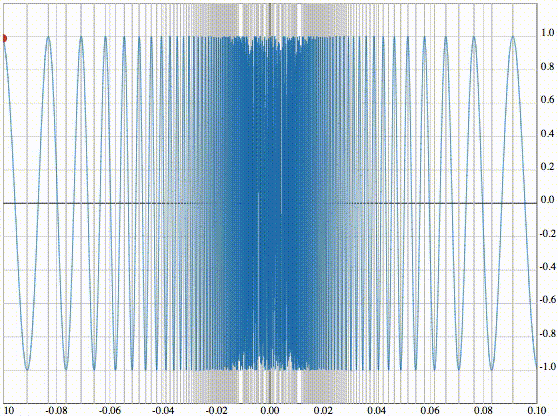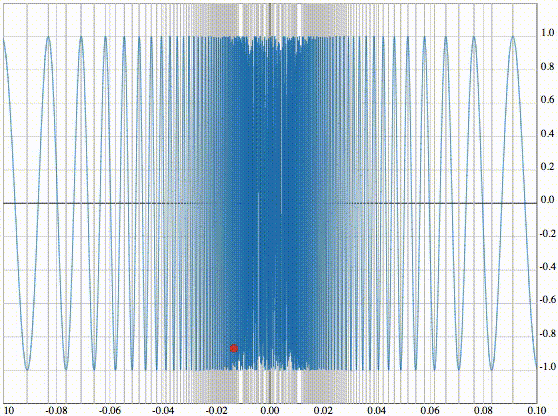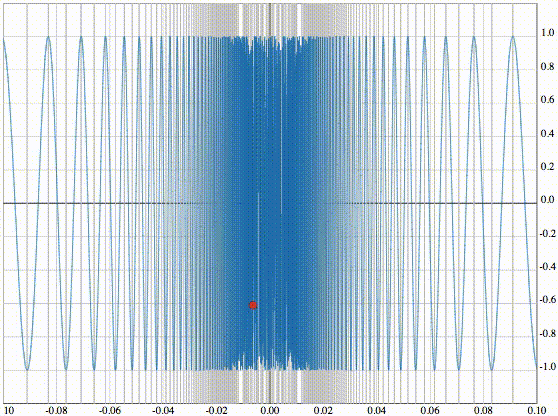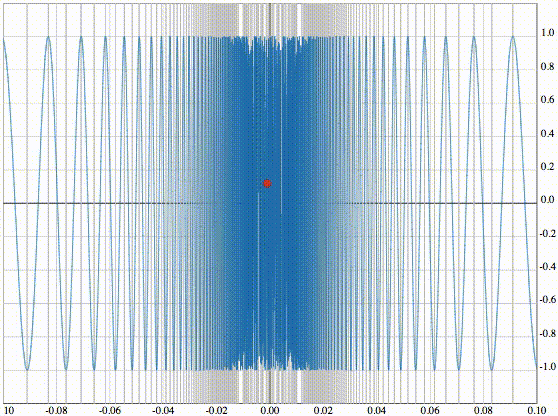
Следующая функция
уже непрерывна в нуле, но, как было понятно из вышеприведенной анимации, она не дифференцируема в этой точке.
Проиллюстрируем это, нарисовав хорду. Угловой коэффициент этой хорды сильно осциллирует при подходе движущейся точки к началу координат. Отсюда видно, что функция не является дифференцируемой в точке x=0
Рассмотрим далее функцию:
Угловой коэффициент хорды стабилизируется при подходе к 0, но касательная беспорядочно меняет своё положение (постоянно меняется её угловой коэффициент). Это происходит из-за того, что функция
не является непрерывно дифференцируемой, т.е. её производная терпит разрыв в точке x=0.
В заключение рассмотрим функцию:
Эта функция непрерывно дифференцируема в точке x=0. Изобразим на графике этой функции движущуюся точку, хорду и касательную. На нижеприведённой анимации видно, что здесь стабилизируется и хорда, и касательная.
Заключение
Таким образом, на наглядных примерах гармонических, степенных функций и их композиций мы рассмотрели природу дифференцируемости различных числовых функций. При этом мы опирались на на стандартные подходы рассмотрения взятия производной в окрестностях точек различного вида, а на «практическом» подходе, при котором производная решает вопрос замены оригинальной функции ее упрощенным линейным представлением.
Выражаем большую признательность за работу Алексею Никитину, Матвею Грицаеву и Алексею Карпову

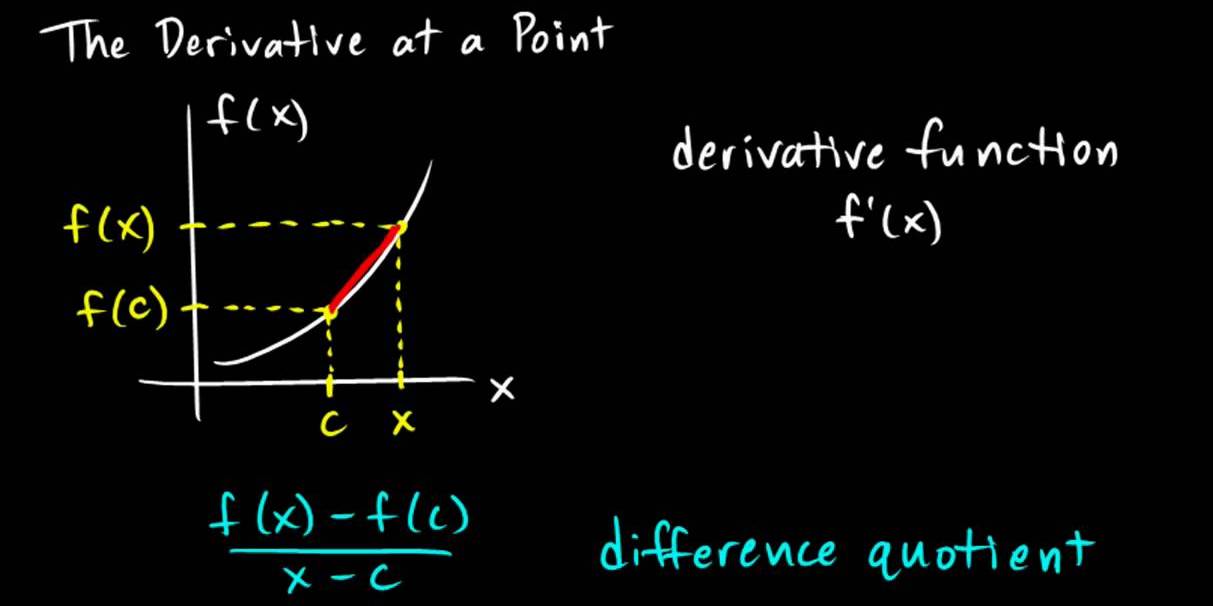



Комментарии