Подборка алгоритмов обхода графа с gif-анимациями и объяснениями. Статья поможет ознакомиться и разобраться с различными методами, которые используются в теории графов.

Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:

• углубишься в решение практических задач;
• узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.

Ты также будешь на связи с преподавателем и другими студентами.

В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂

Интересно, хочу попробовать

Depth-First Search(s) - Поиск в глубину

Из названия этого метода обхода графа ясно, что в процессе поиска мы идем «вглубь» графа настолько, насколько возможно. Следуя алгоритму, мы последовательно обойдем все вершины графа, которые доступны из начальной вершины. Если ребро ведет в не пройдённую до этого момента вершину, то алгоритм запускается с нее. В случае если ребер, которые ведут в не рассмотренную вершину, больше нет, то происходит возврат назад.

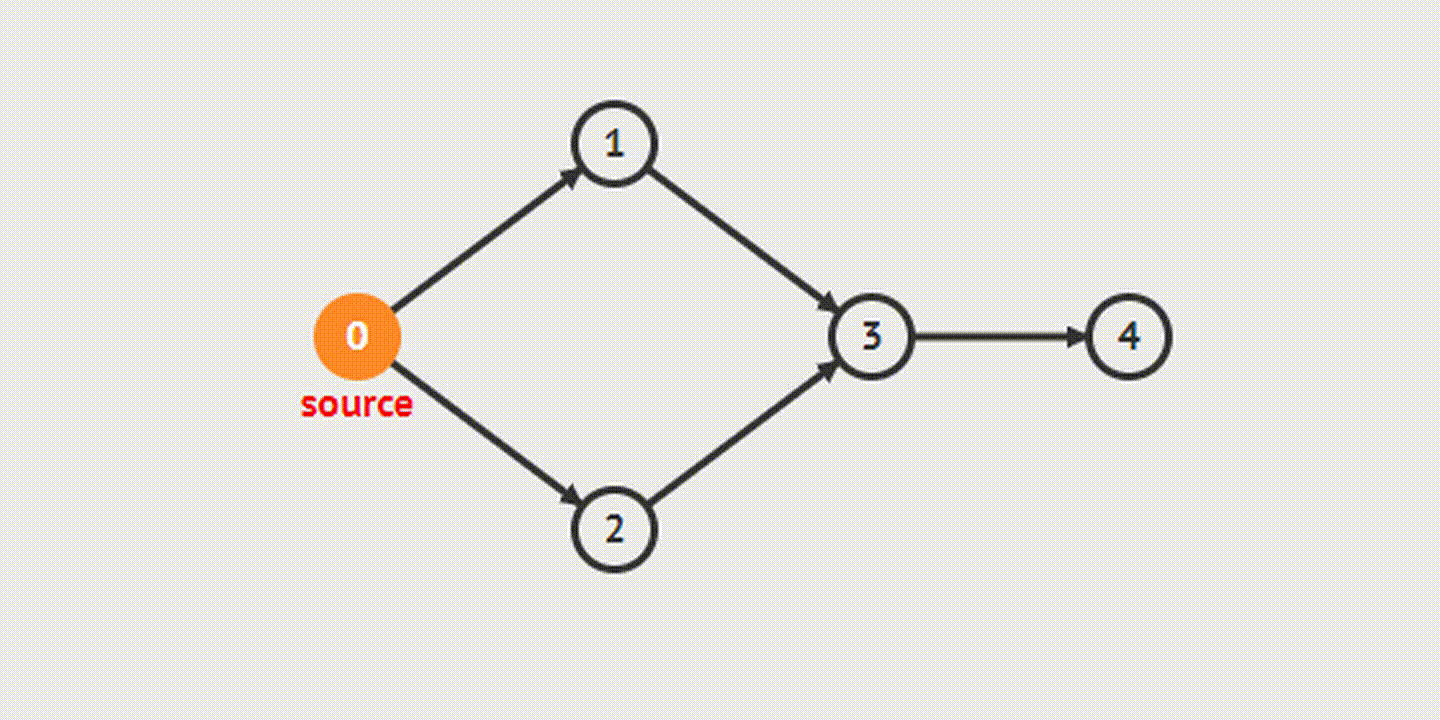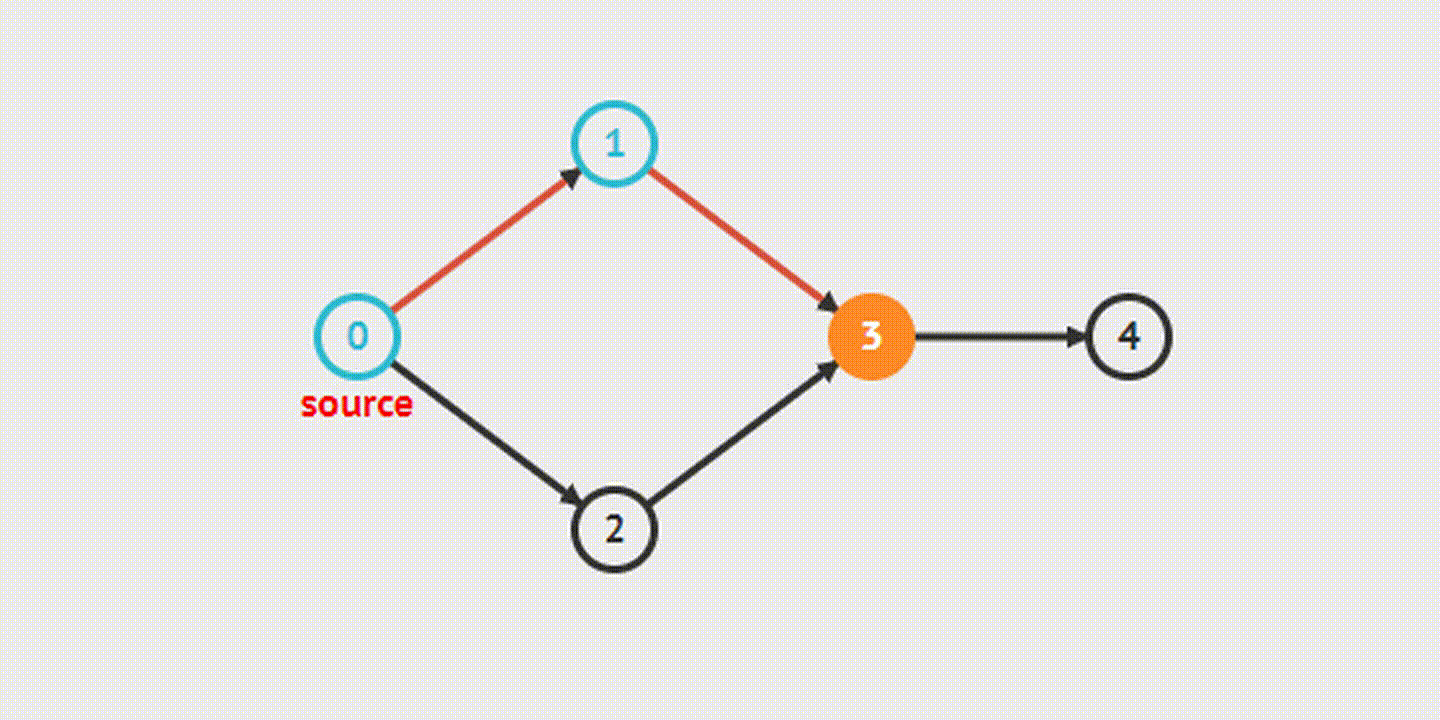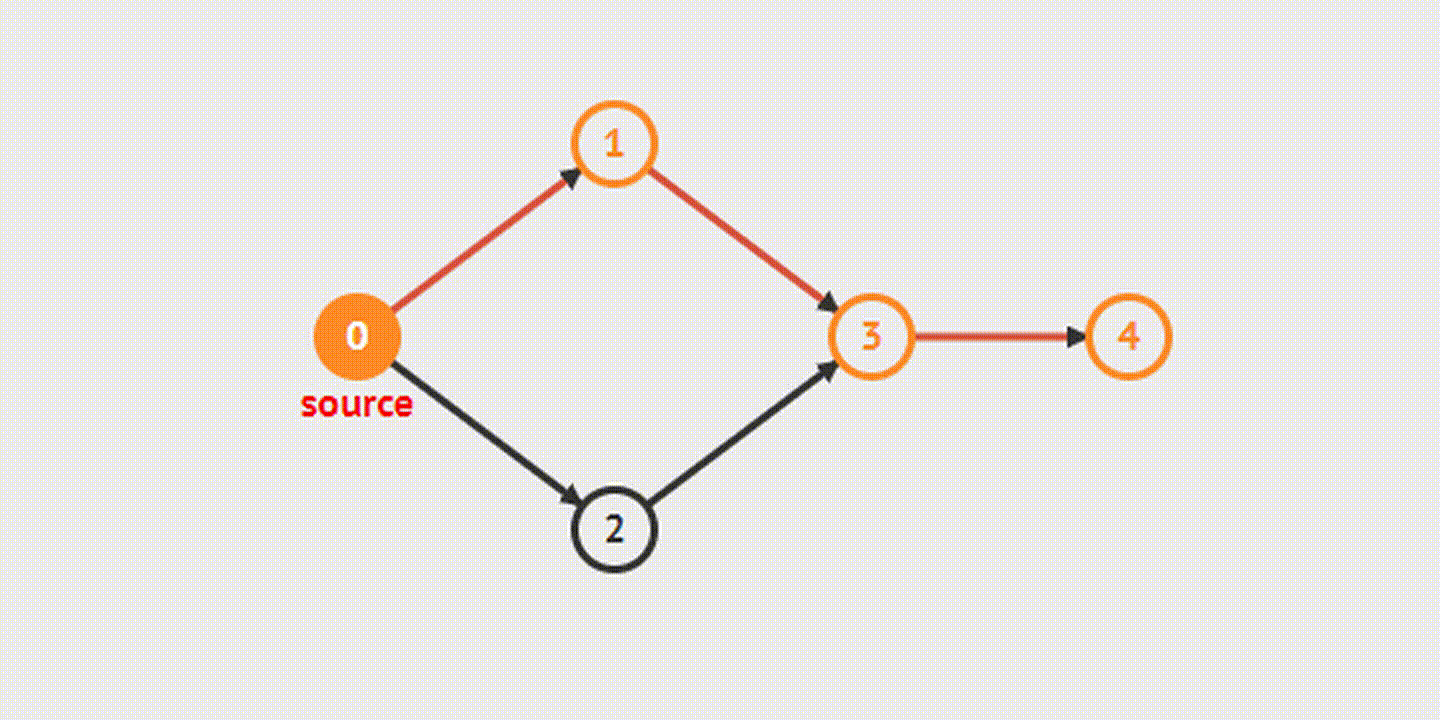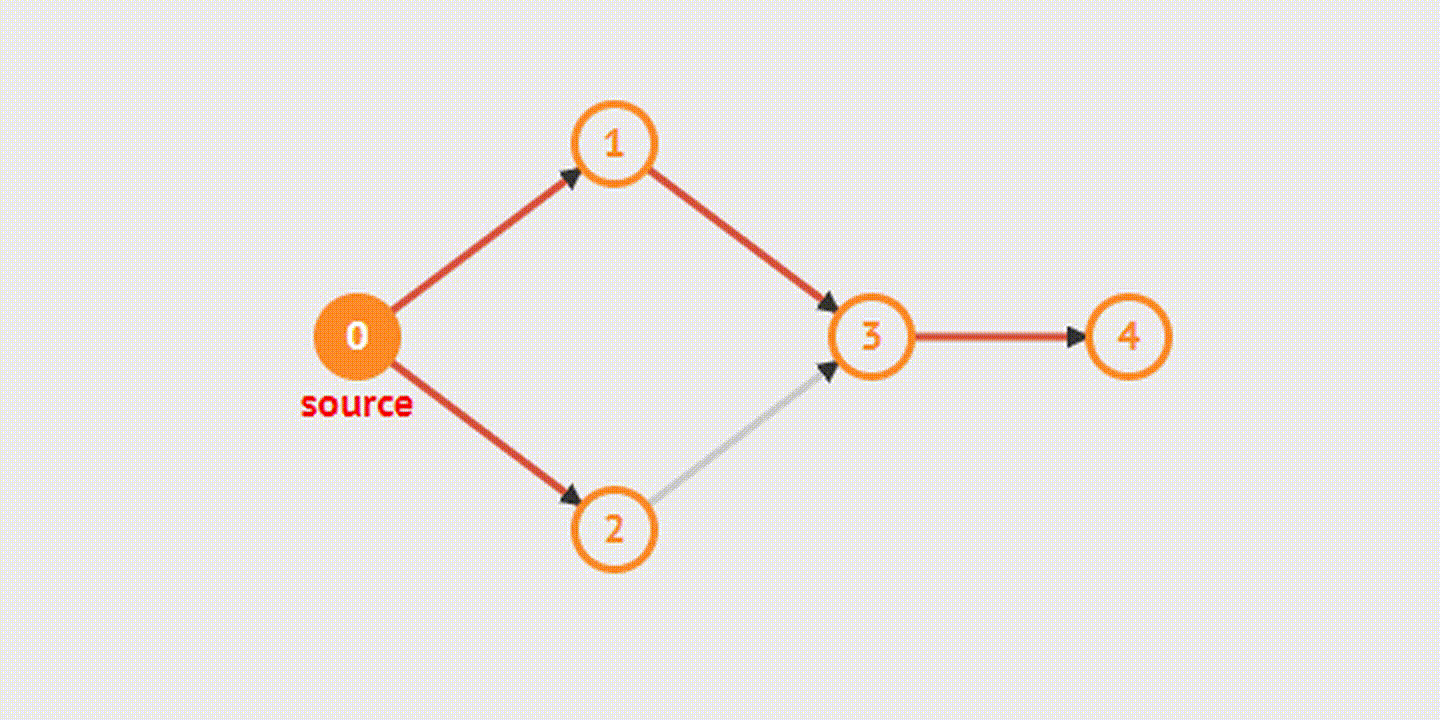
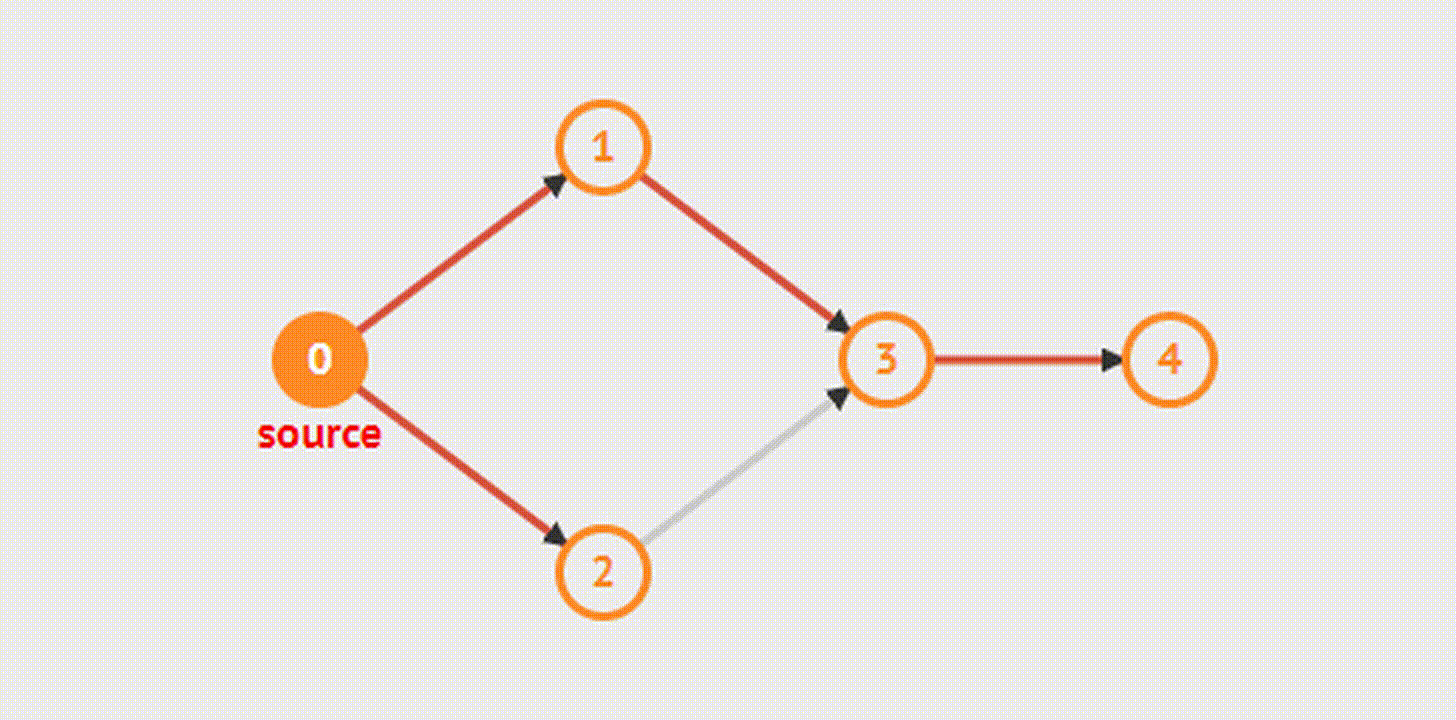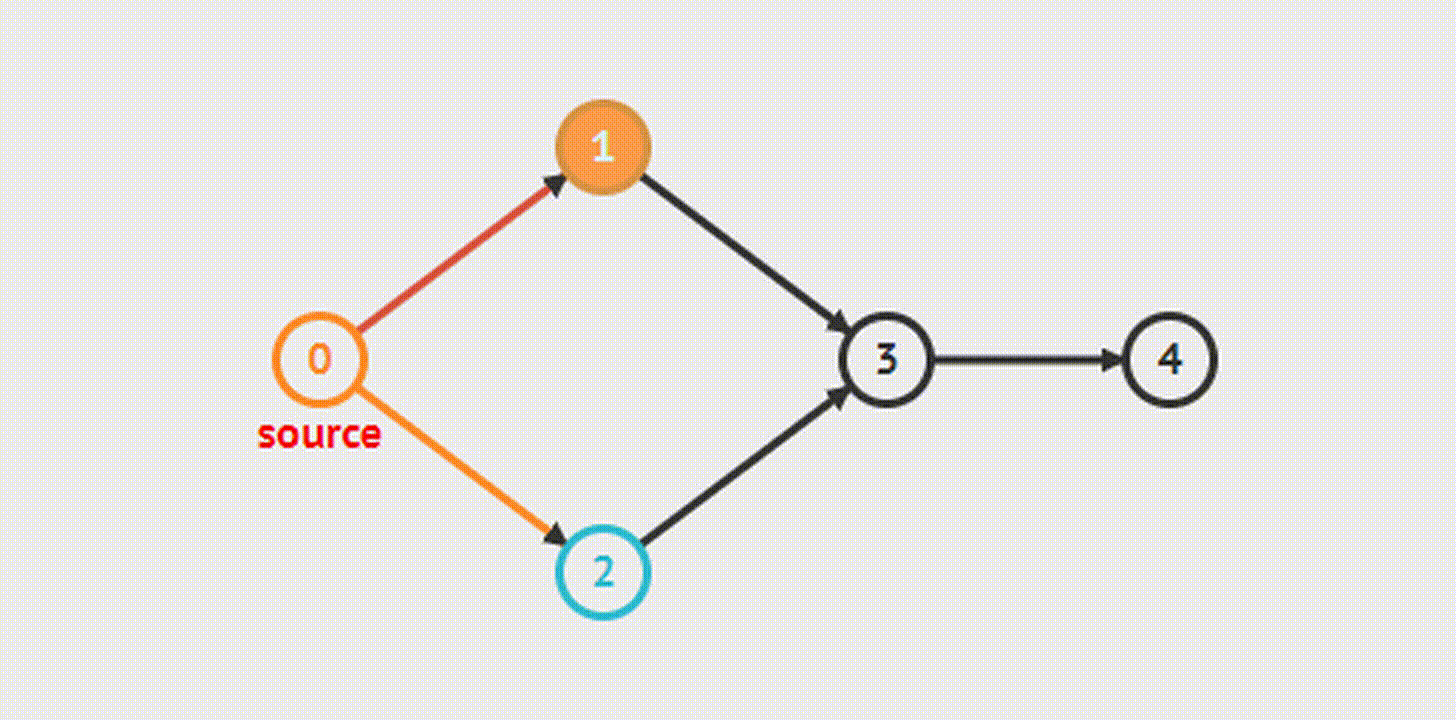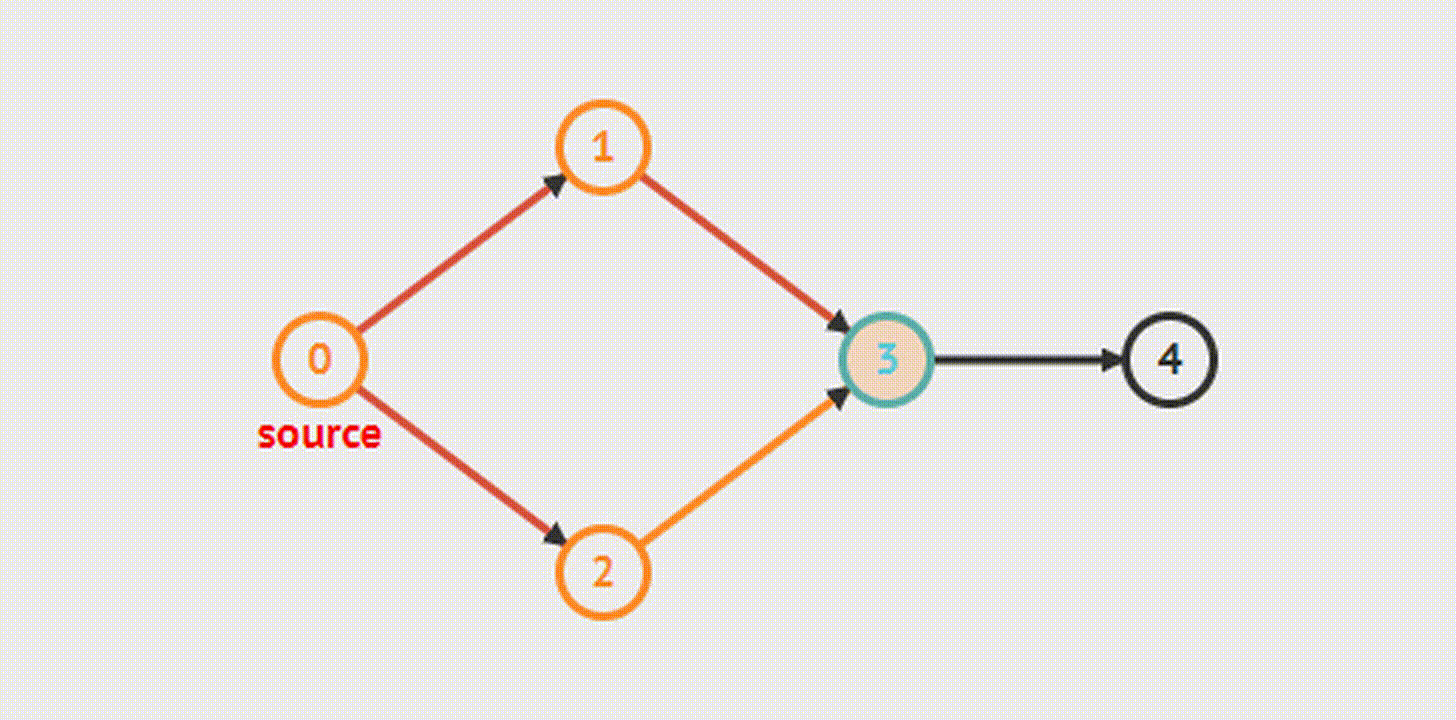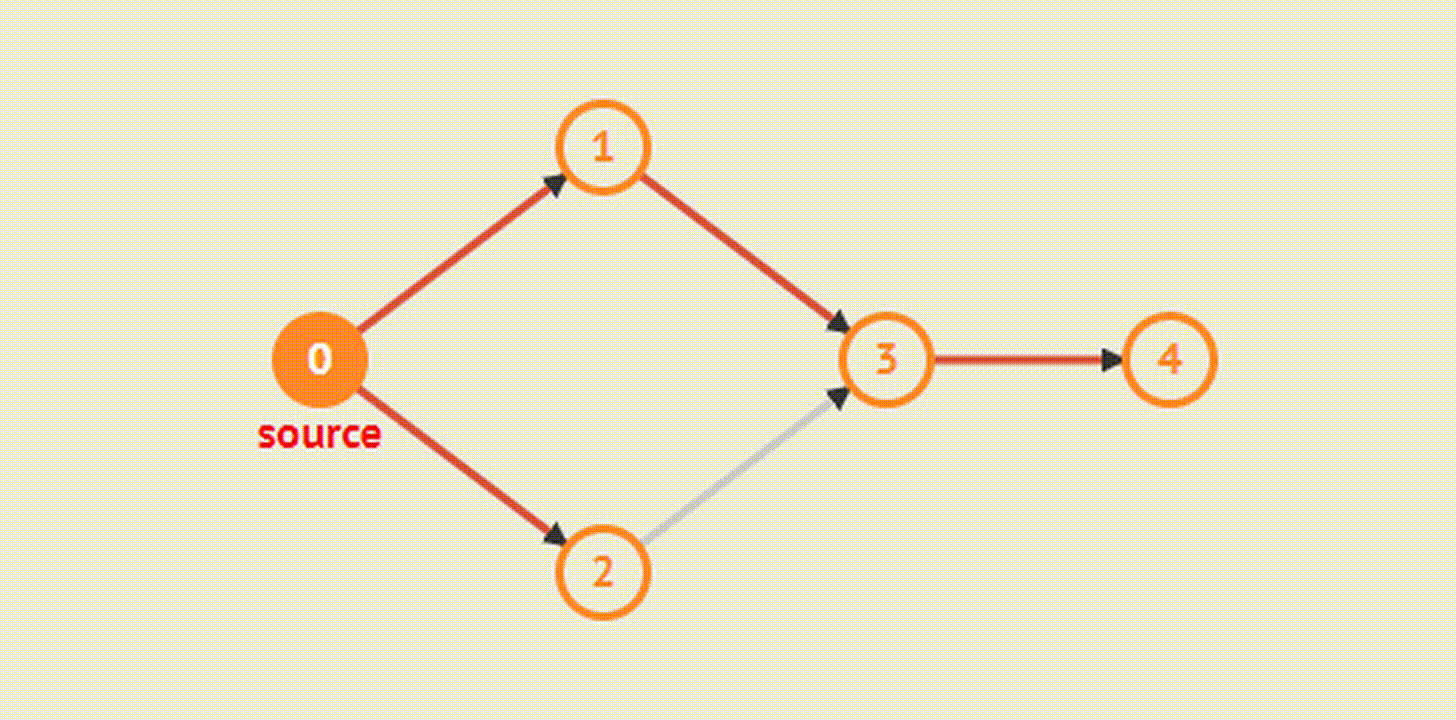
Breadth-First Search(s)- Поиск в ширину

Алгоритм позволяет найти кратчайший (содержащий наименьшее число ребер) путь из одной вершины графа до всех остальных вершин. В нем сначала посещаются все вершины, смежные с текущей, а затем их потомки.

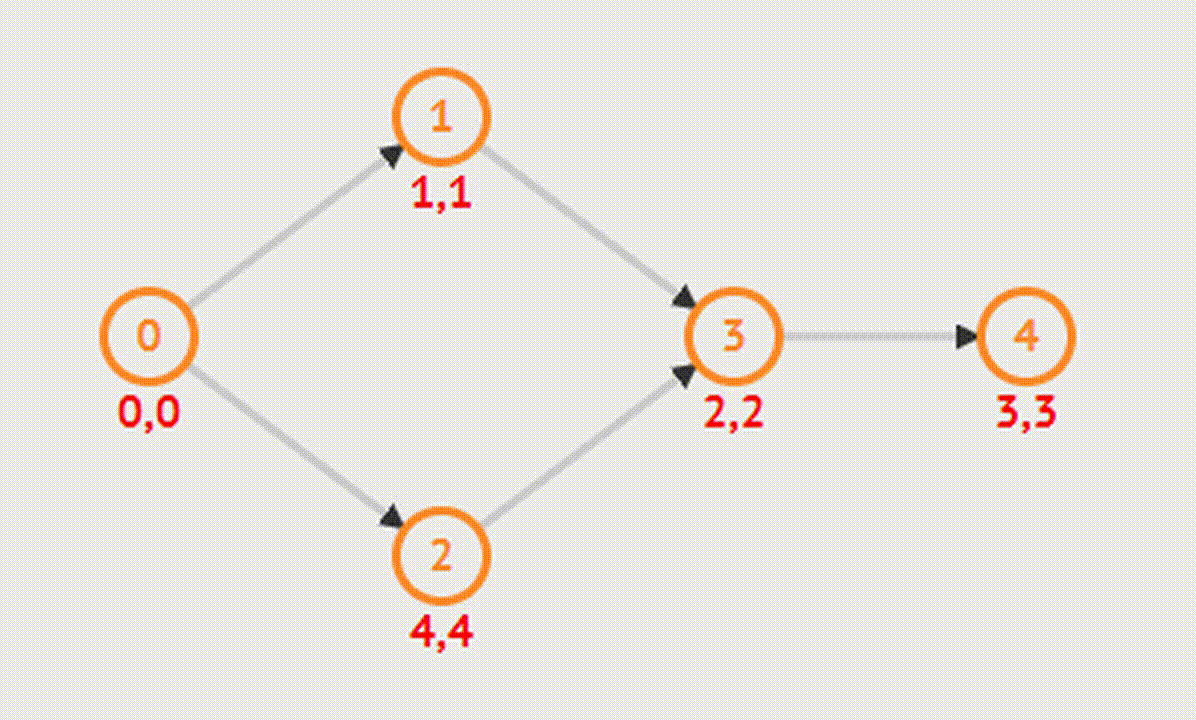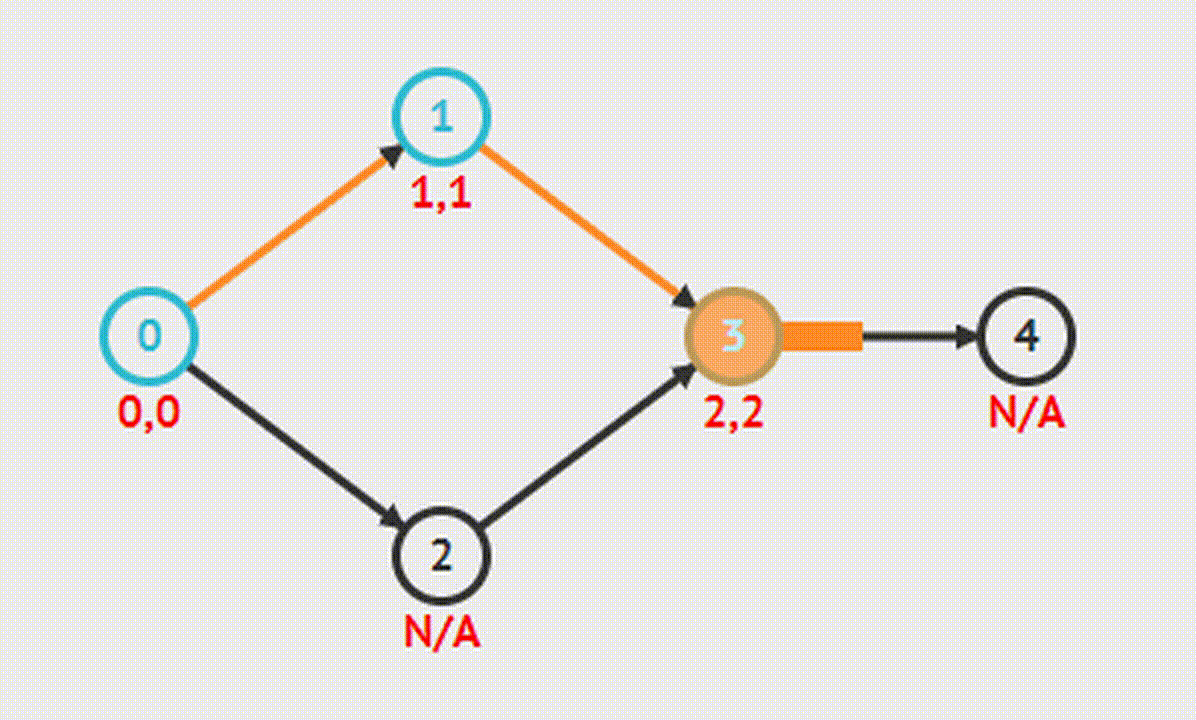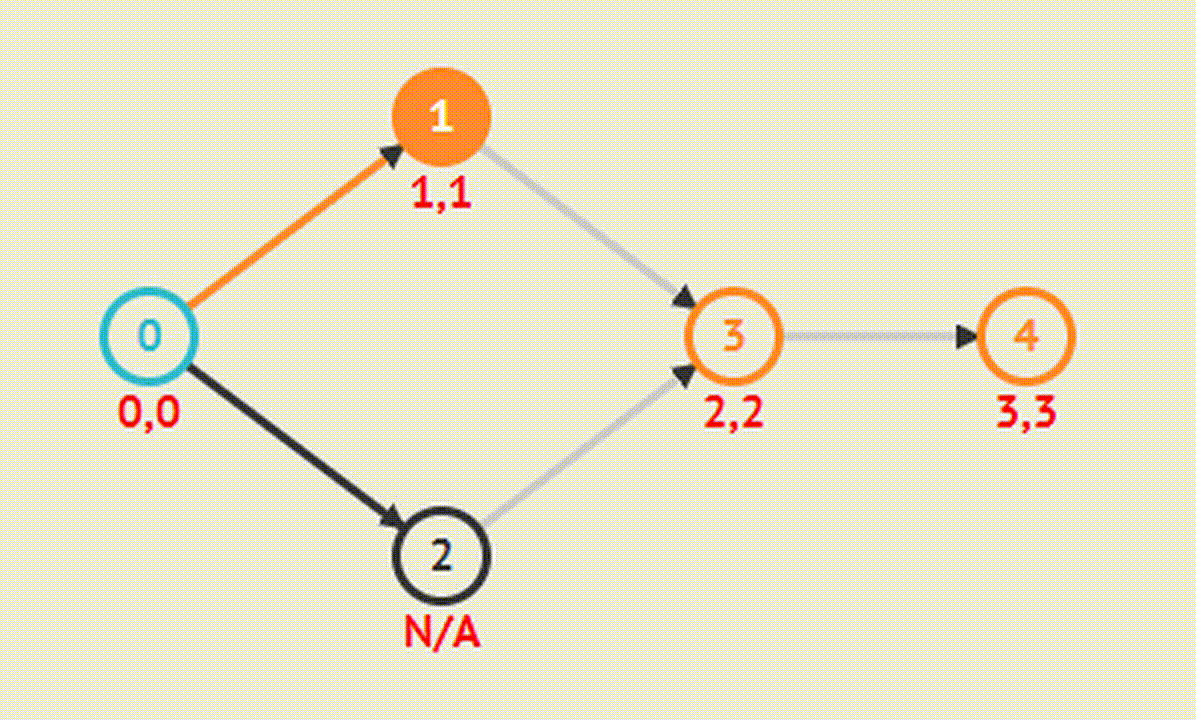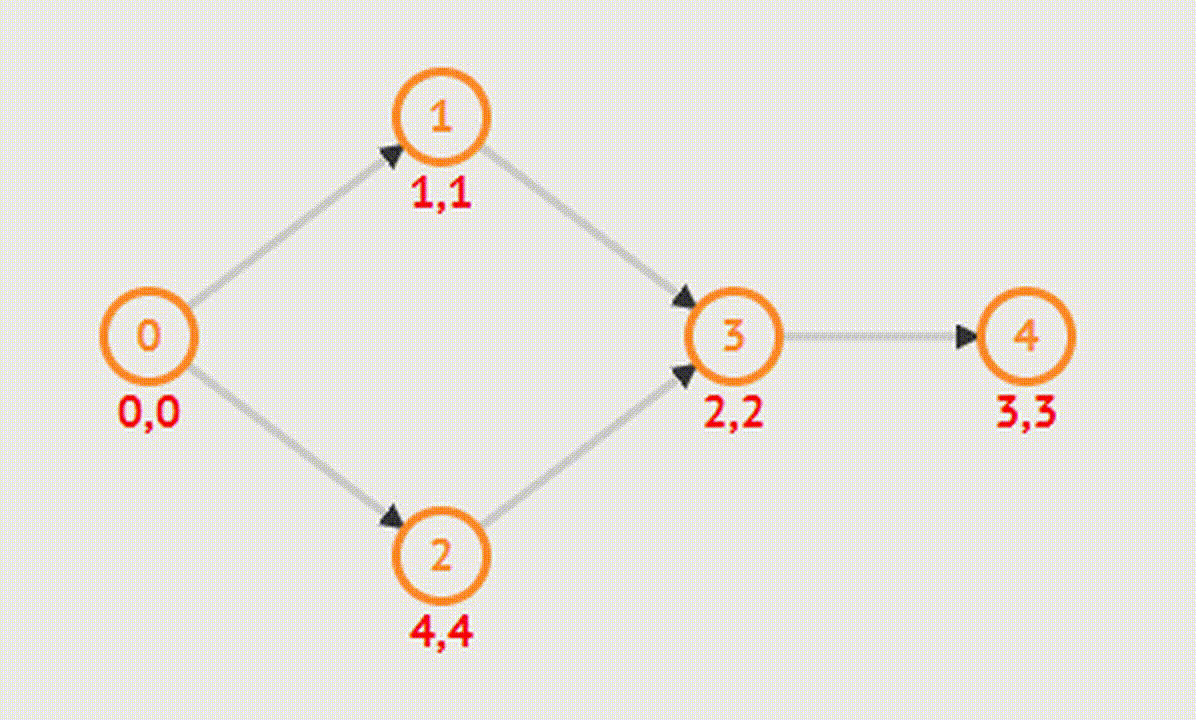
Topological Sort: Топологическая сортировка

Является упорядочиванием вершин бесконтурного ориентированного графа. Его цель состоит в том, чтобы перенумеровать вершины так, чтобы каждое ребро из вершины с меньшим номером вело в вершину с большим. Иными словами, нужно найти перестановку вершин, которая соответствует порядку, задаваемому всеми ребрами графа.

DFS

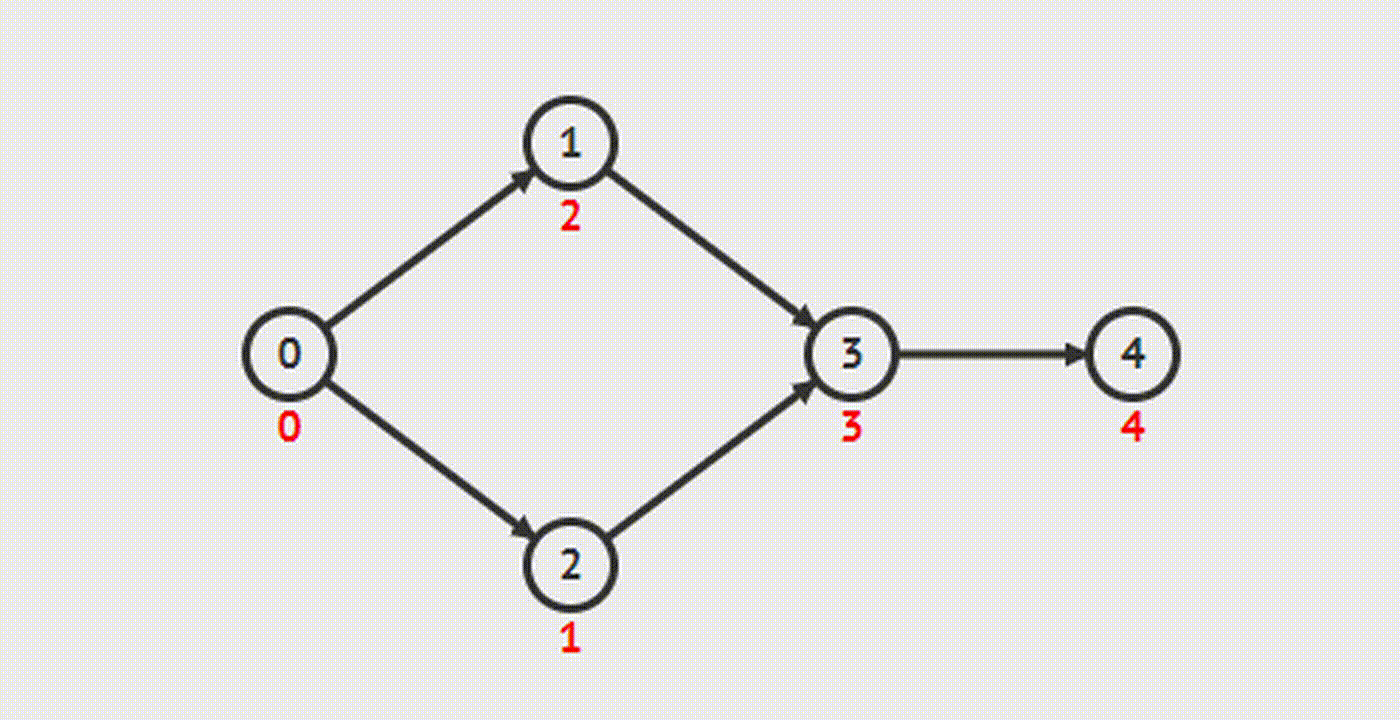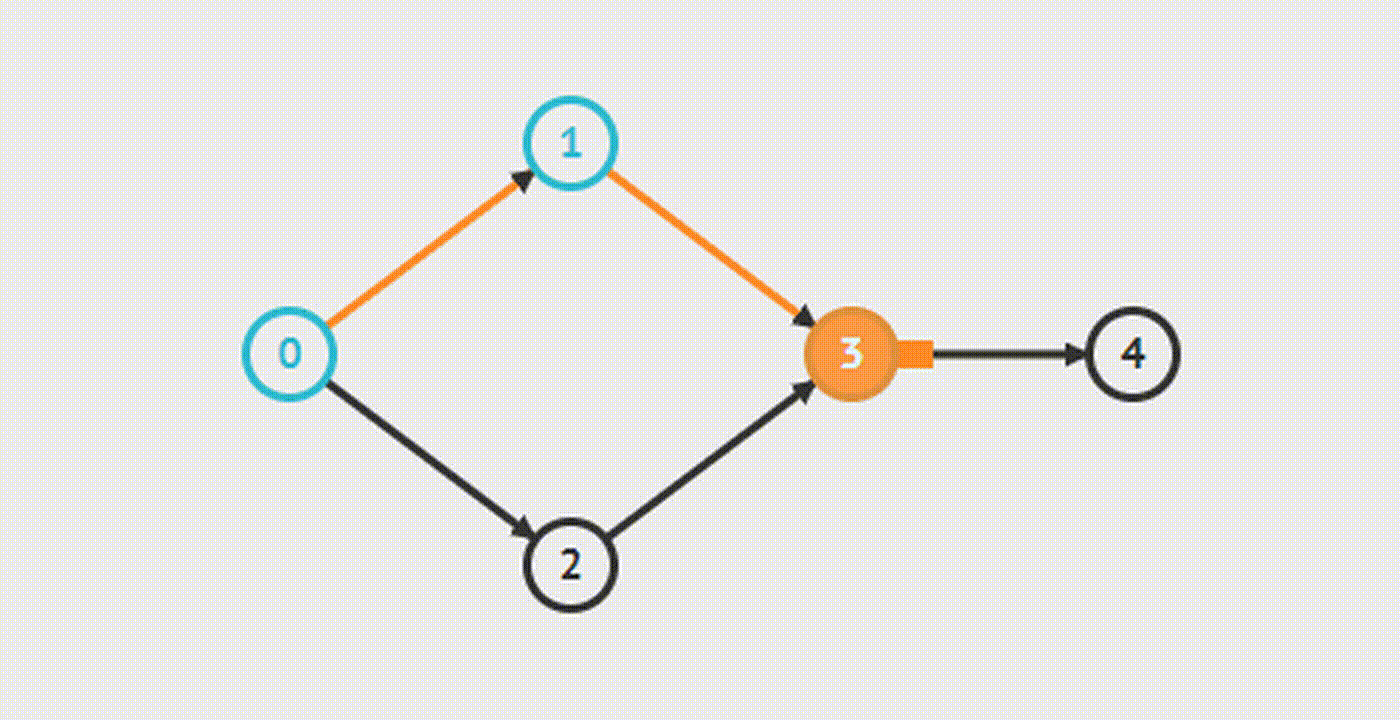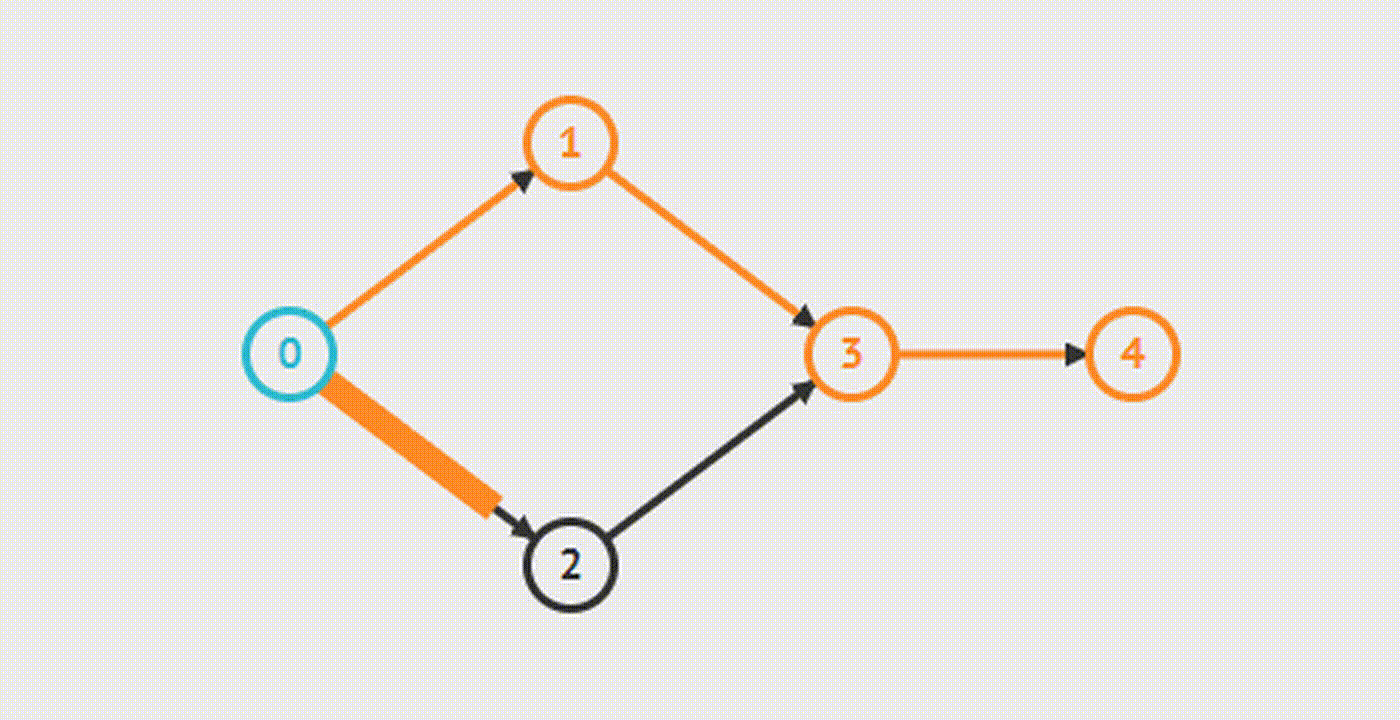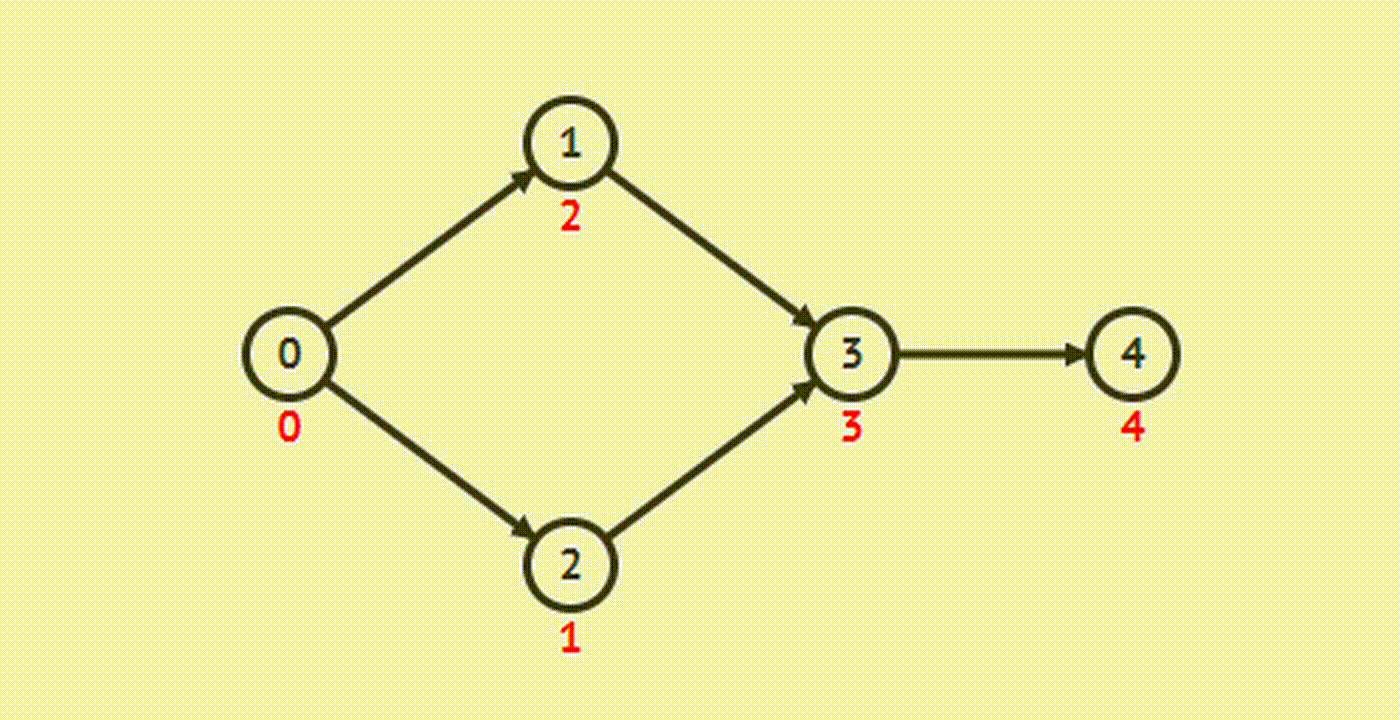
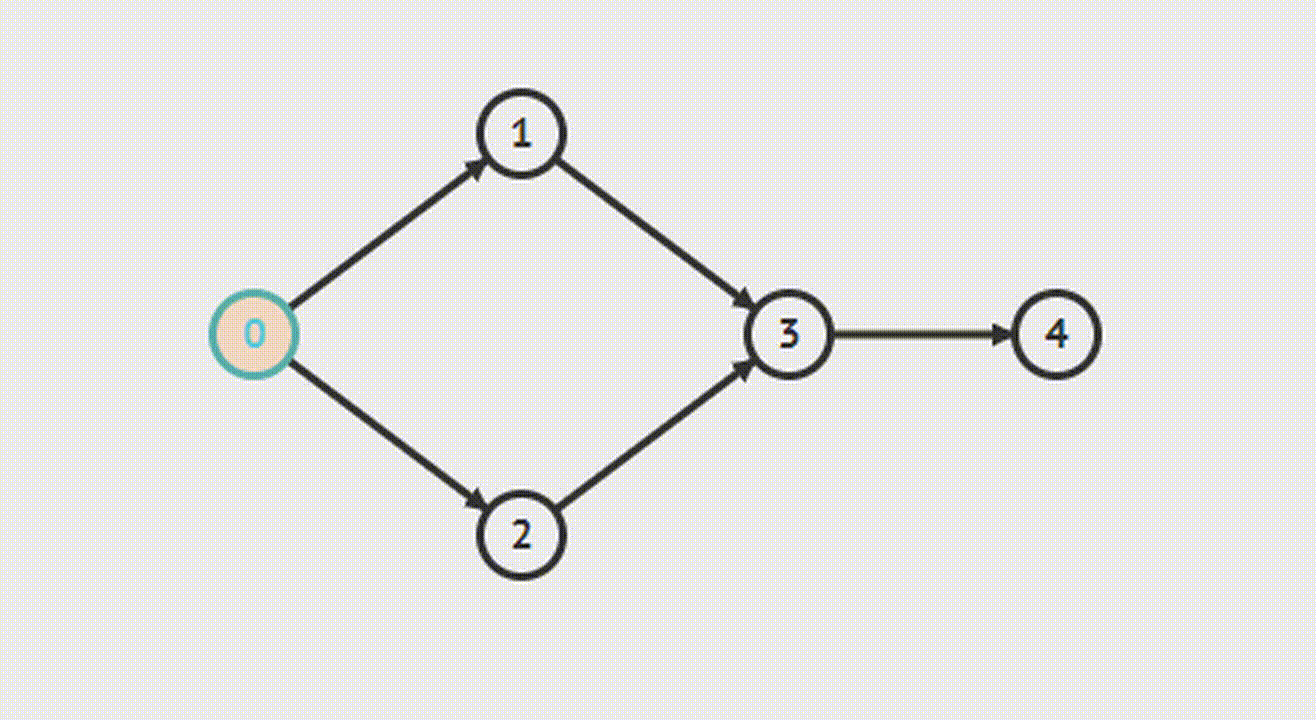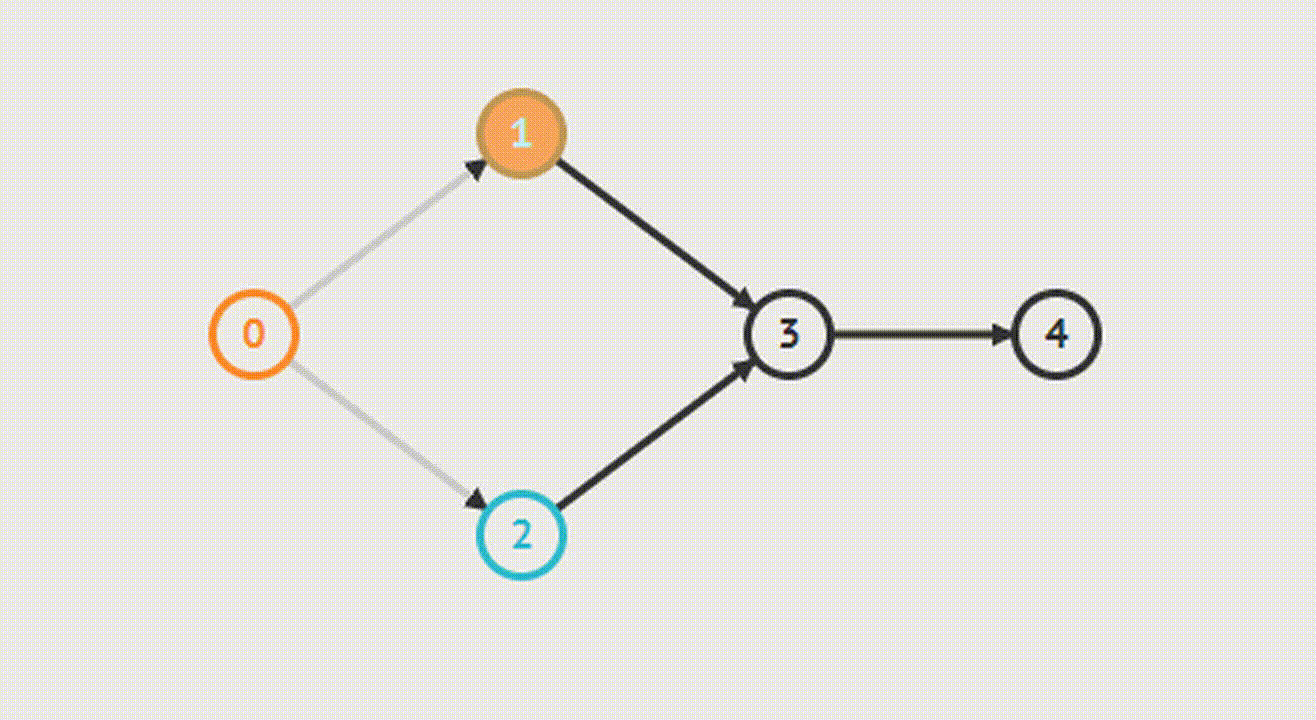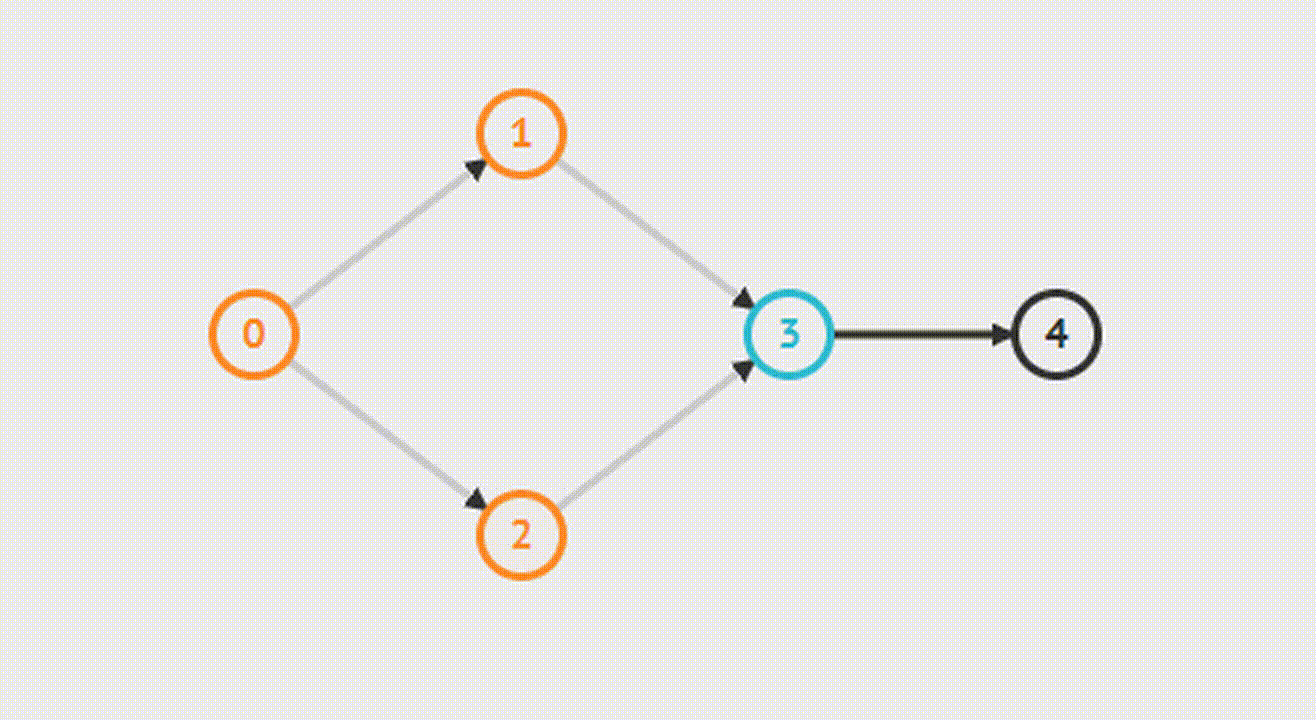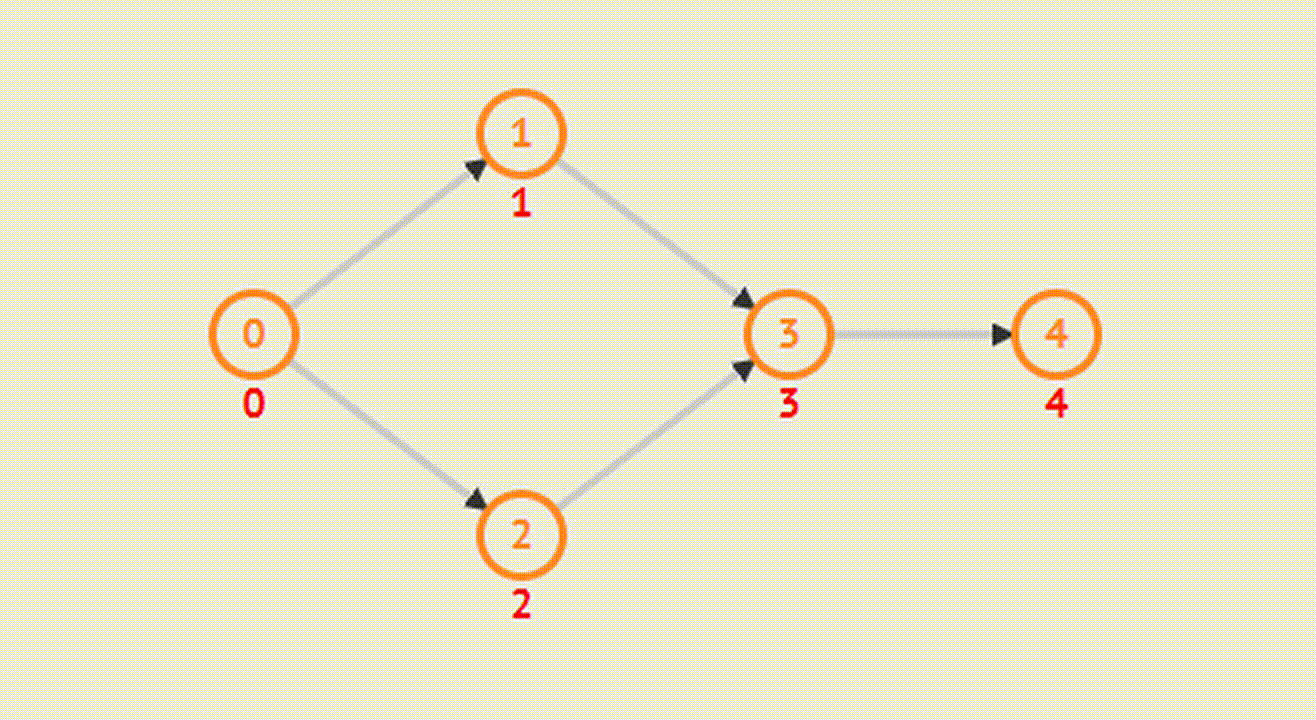
BFS (Kahn’s algorithm)

Алгоритм основывается на выборе вершин в порядке, подобном топологической сортировке. Сначала находим список начальных вершин, которые не имеют входящих граней, и помещаем их в множество S. В непустом ациклическом графе должна существовать хотя бы одна такая вершина.
После этого количество посещённых вершин увеличивается на 1, а степень всех соседних вершин уменьшается на 1. Если после этого степень соседних вершин обнулится, они помещаются в очередь. Этот шаг будет повторяться, пока очередь не опустеет. Если в итоге количество посещенных вершин не будет равно числу вершин на графе, то сортировка невозможна.

SCC Algorithms: Компонента сильной связности в орграфе

Максимальные по включению сильно связные подграфы.

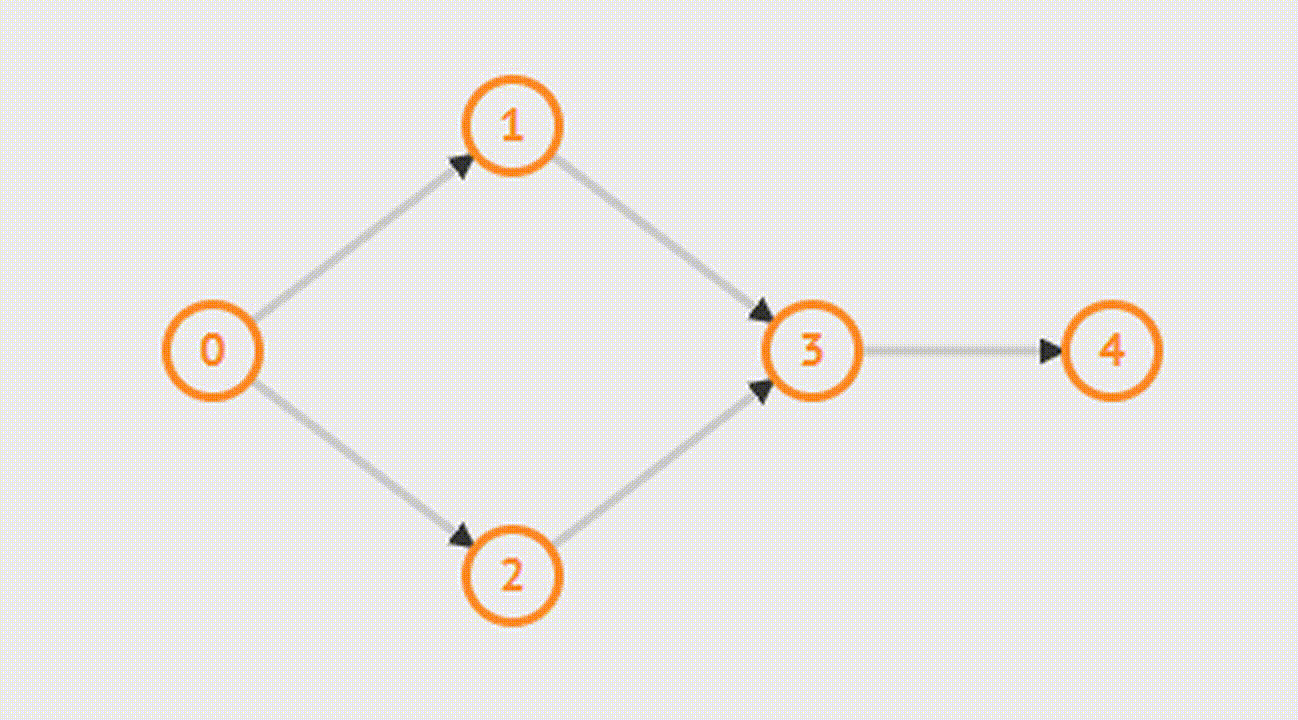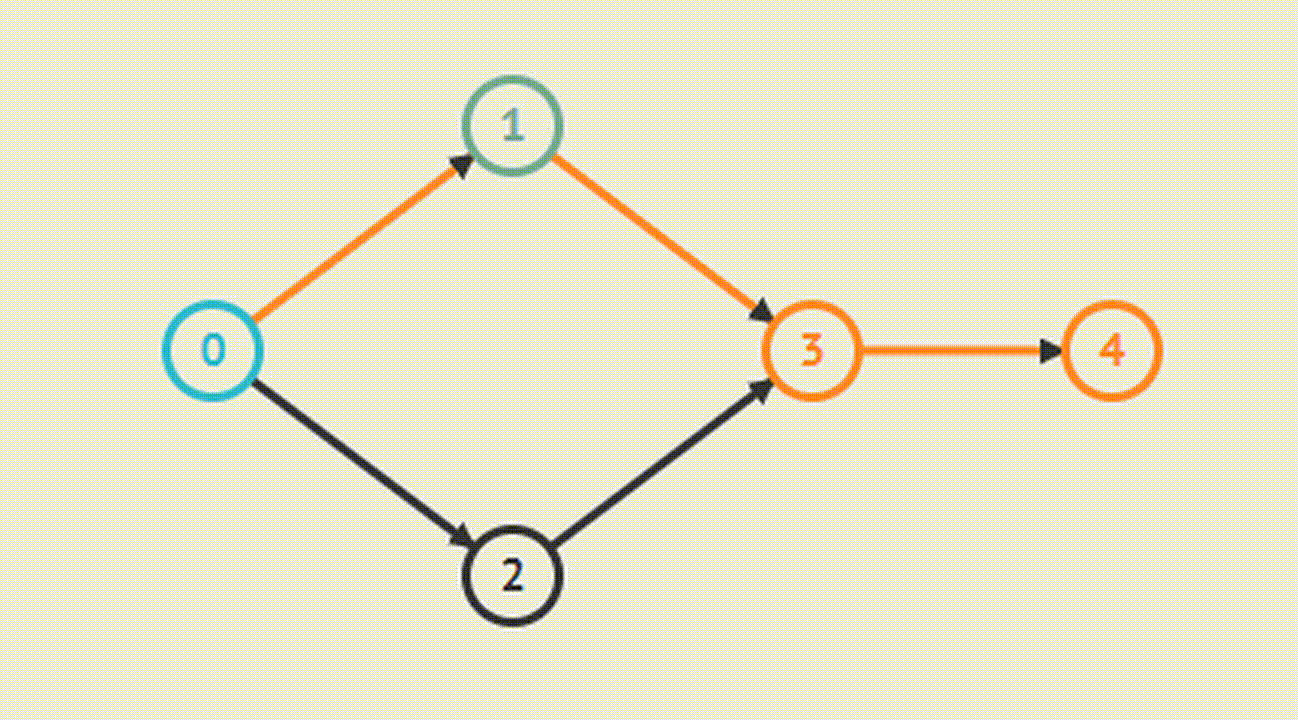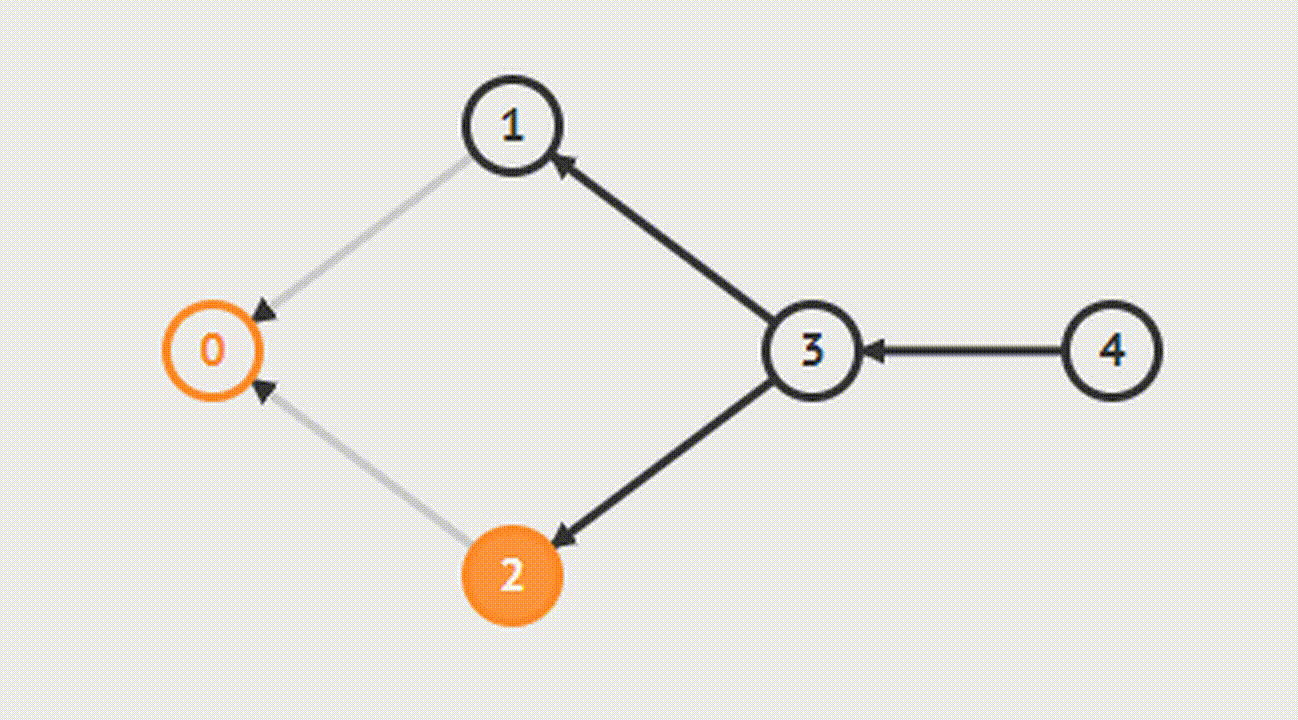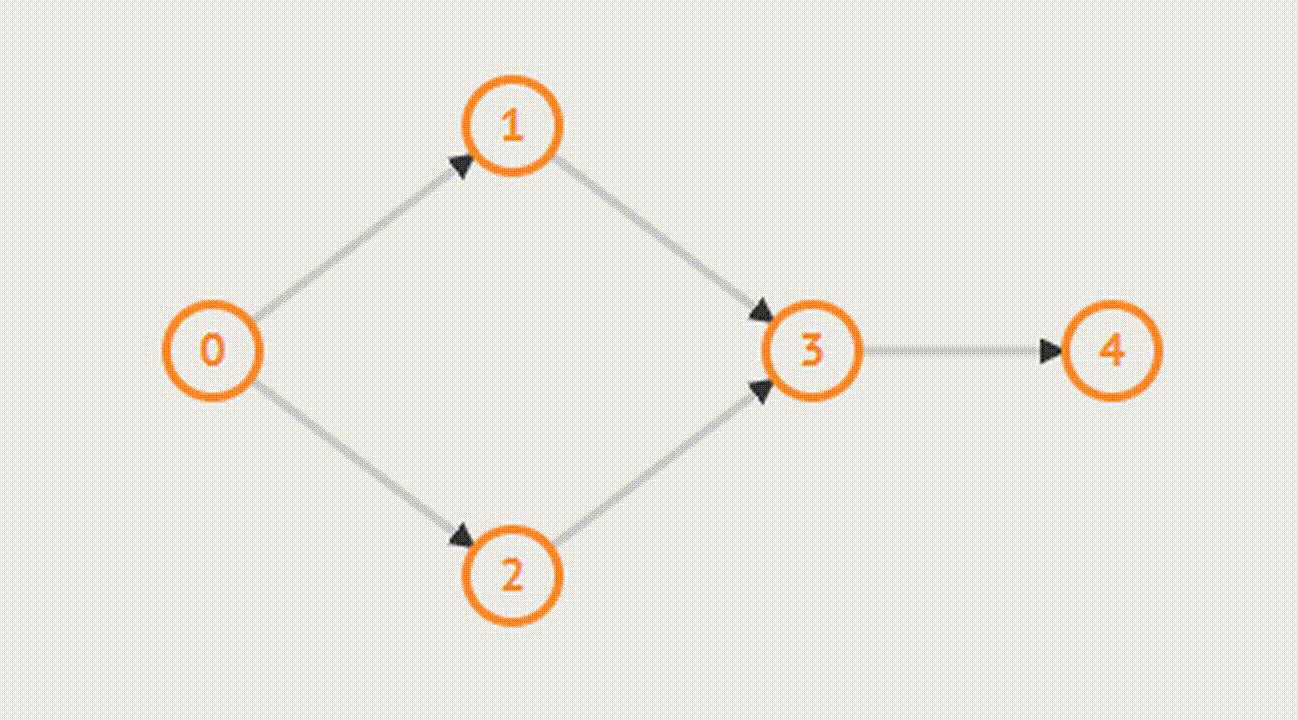
Kosaraju's Algorithm-Алгоритм Косарайю

Для того чтобы найти компоненты сильной связности, сначала выполняется поиск в глубину, каждый раз выбирается не посещенная вершина с максимальным номером, который был получен при обратном проходе. Полученные деревья являются сильно связными компонентами.

Tarjan's Algorithm-Алгоритм Тарьяна

Этот алгоритм в первую очередь представляет из себя один из вариантов поиска в глубину. Вершины посещаются от корней к листьям, а окончание их обработки происходит на обратном пути.

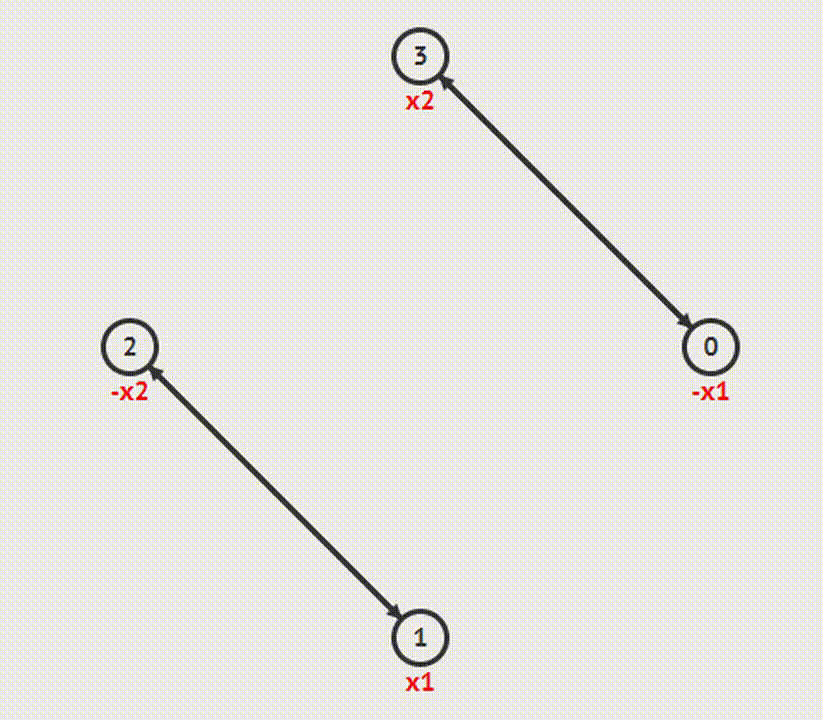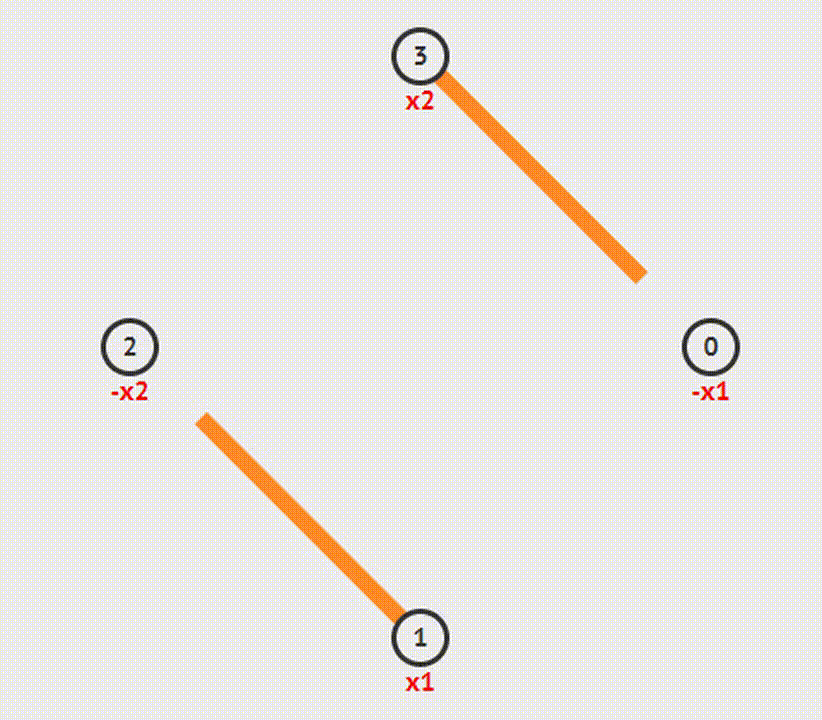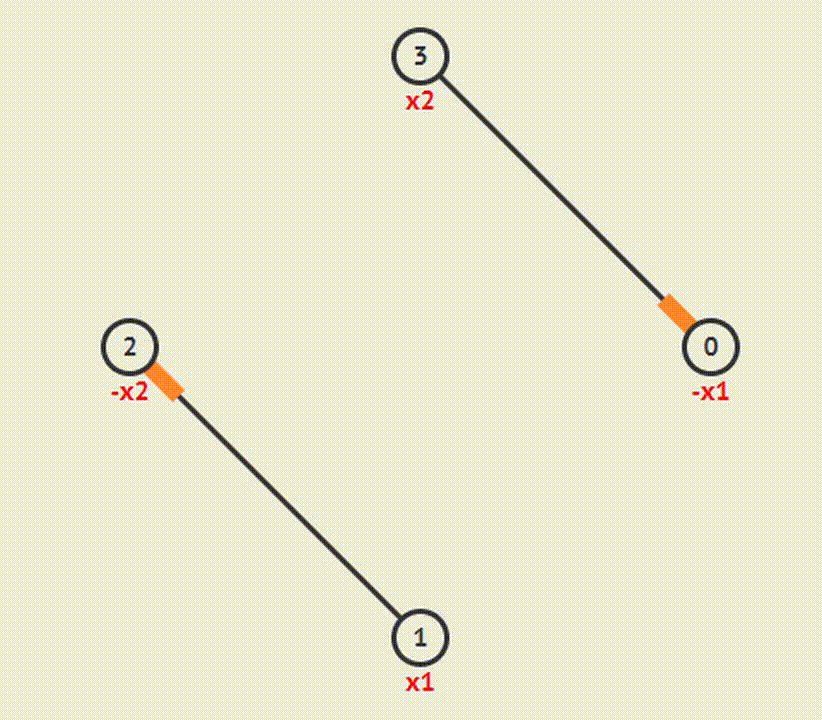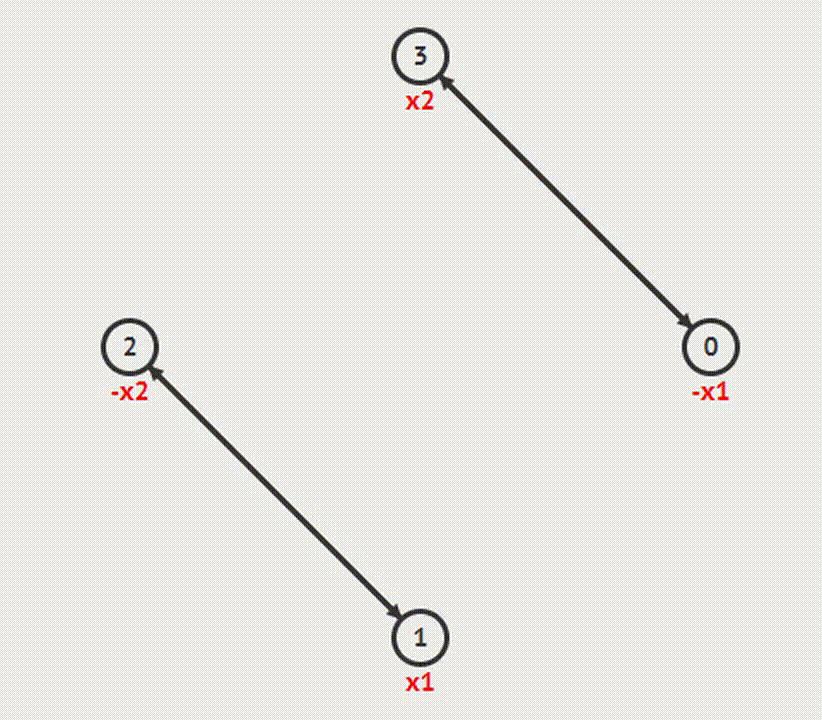
2-SAT Checker (2-satisfiability – 2-выполнимость)

Задача 2-SAT состоит в том, чтобы задать переменным значения таким образом, чтобы формула стала истиной. Алгоритм этой задачи состоит из следующих шагов:

1. Строим граф импликаций
2. Затем находим компоненты сильной связности
3. Проверяем, чтобы для каждой переменной х вершины х и !х лежали в разных компонентах. Если это условие не верно, решения не существует.

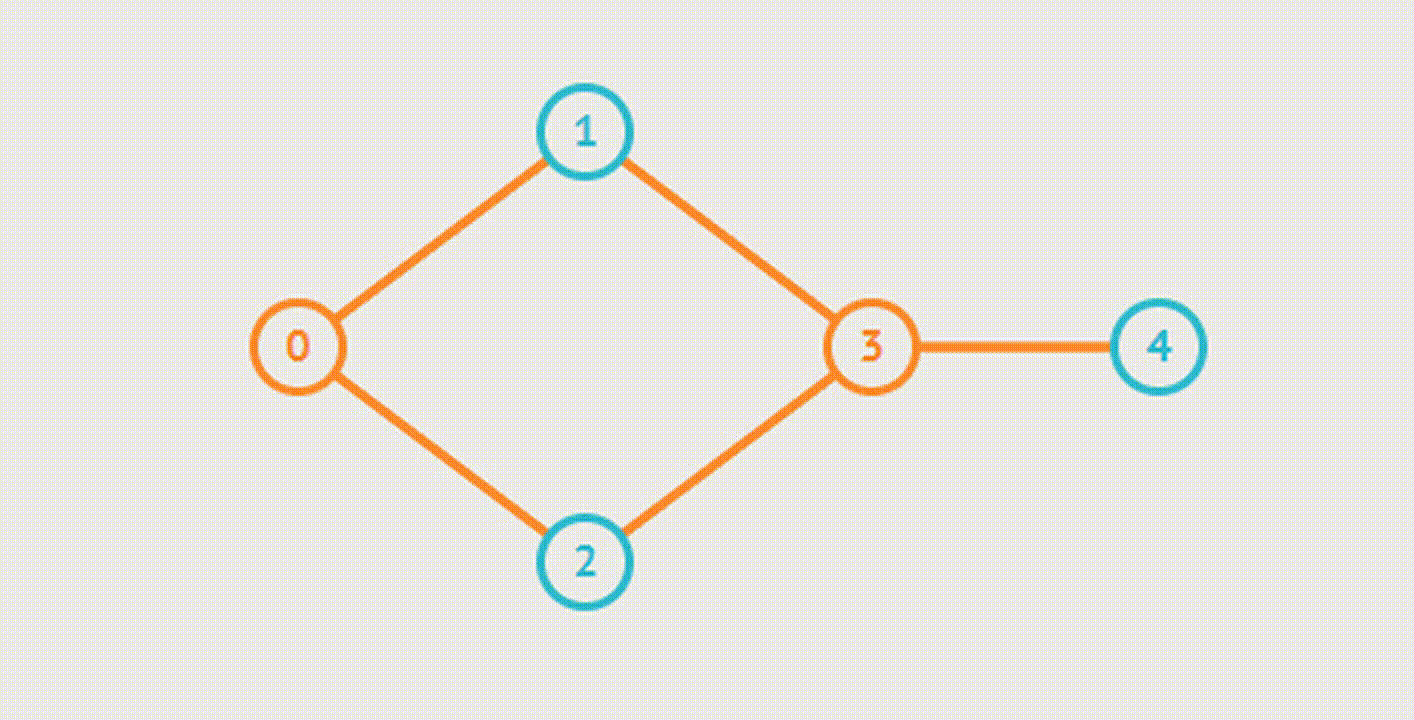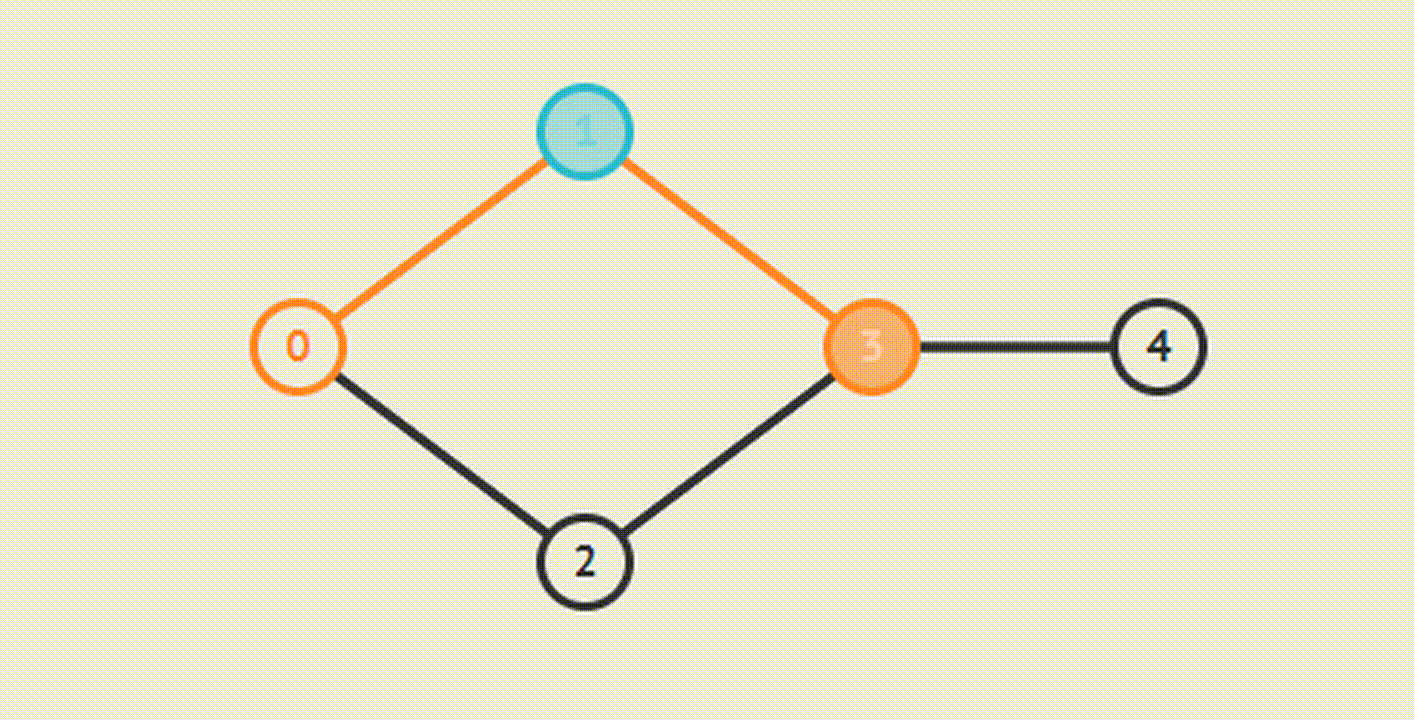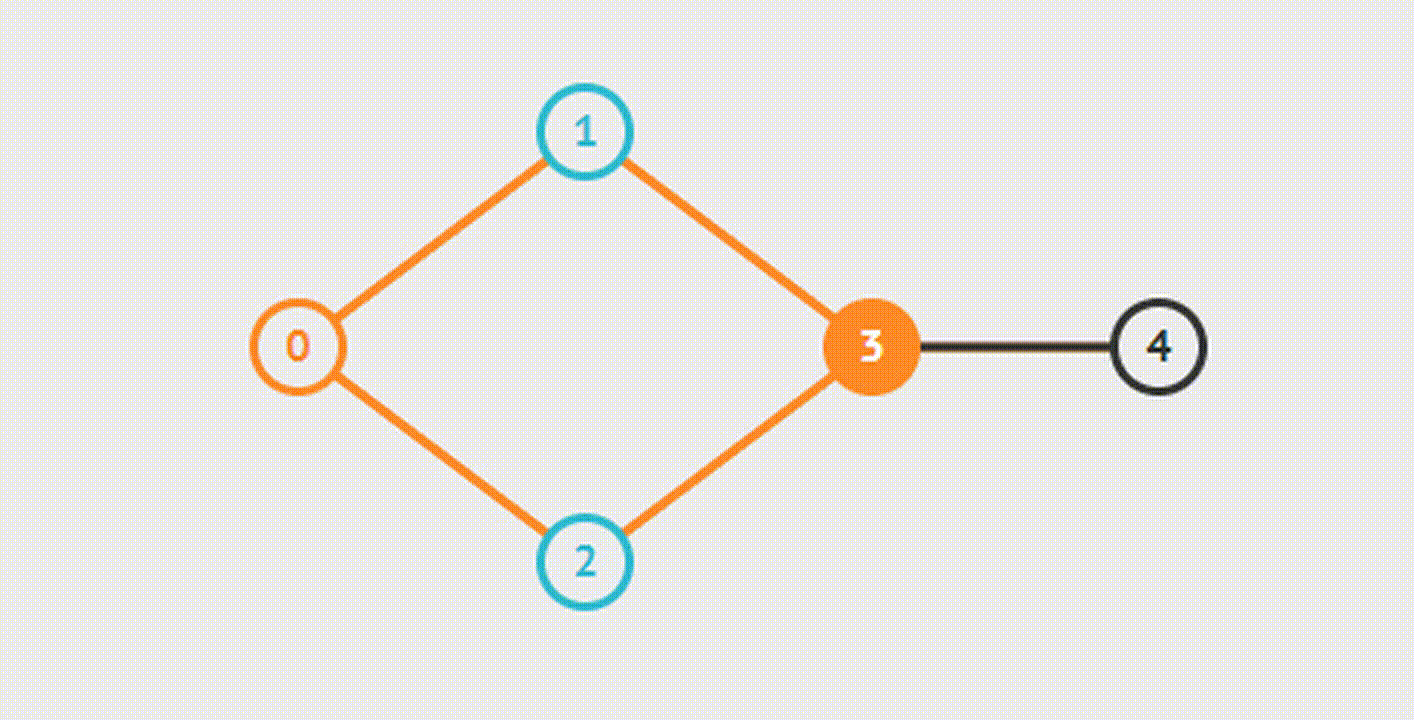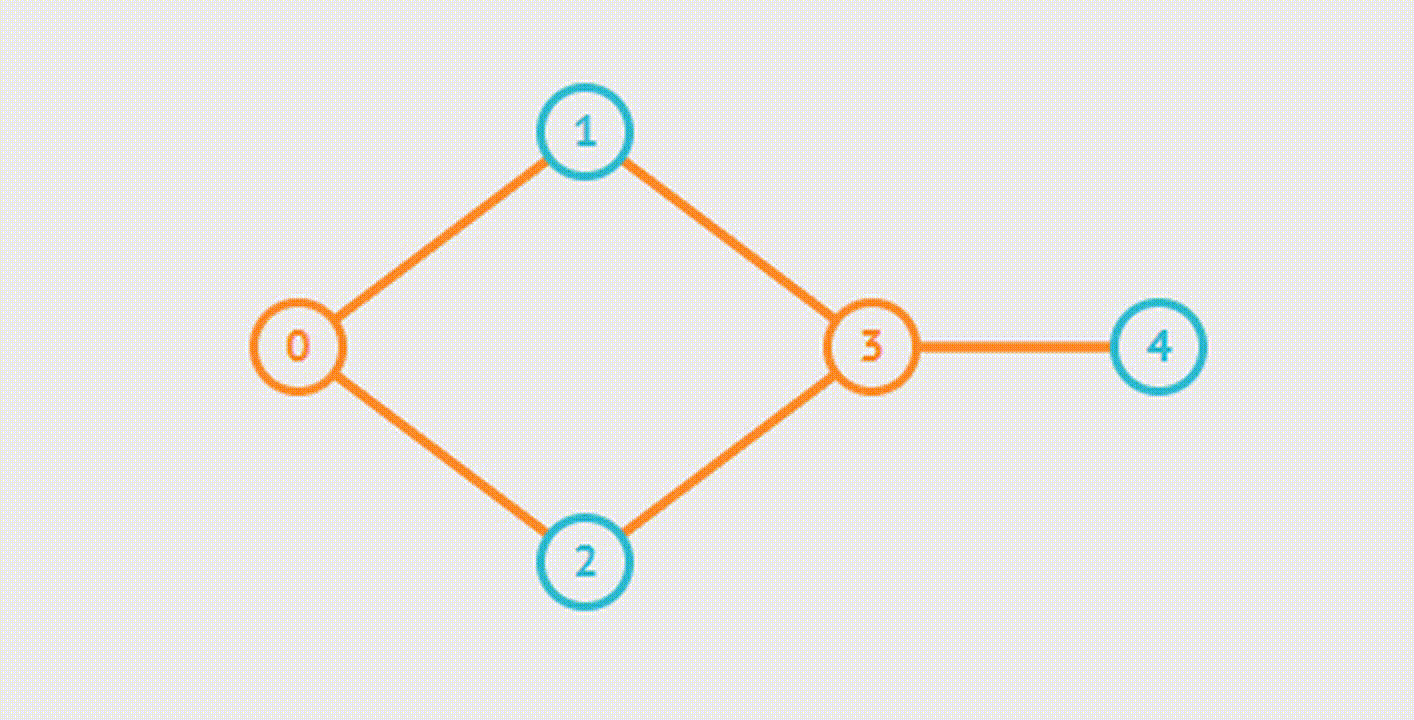
Bipartite Graph Check-Проверка графа на Двудольность

Двудольность графа подразумевает возможность разделения множества вершин графа на две части таким образом, чтобы каждое ребро графа соединяло вершины из этих частей.

BFS

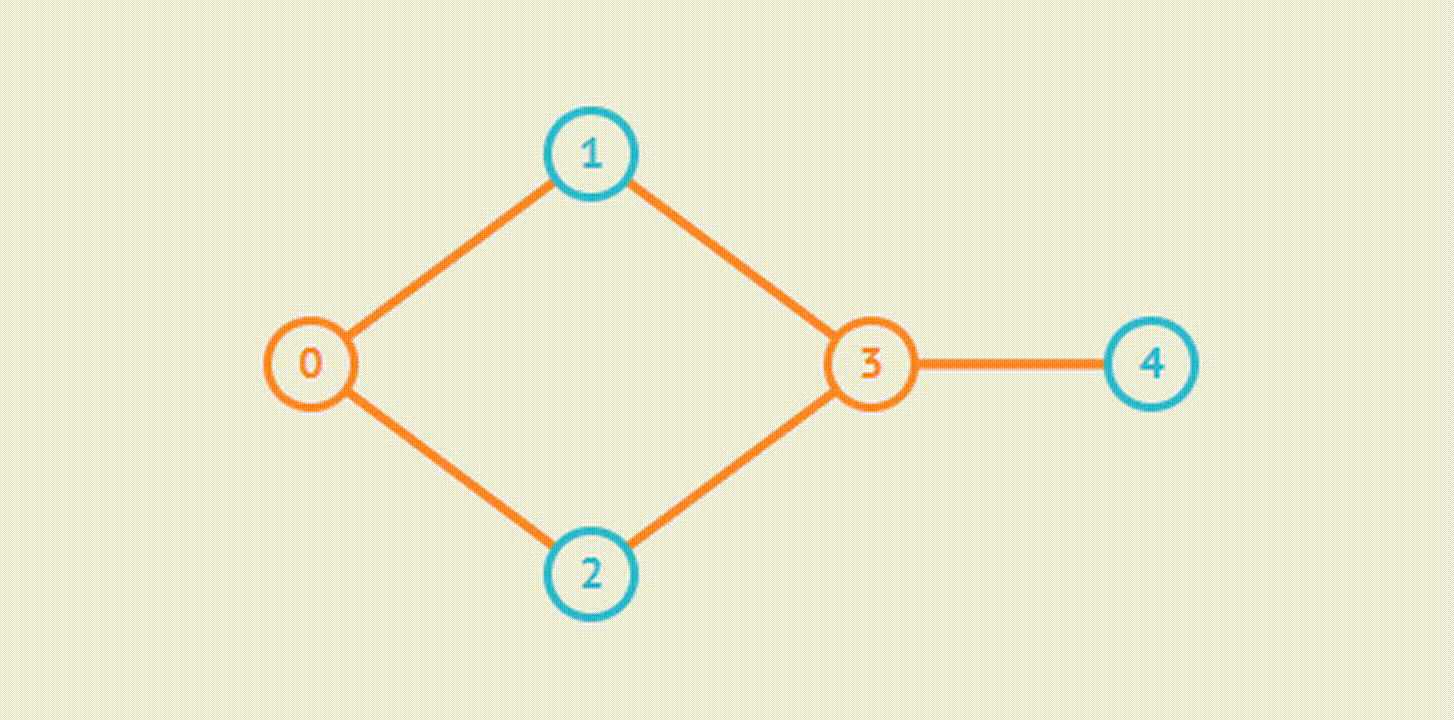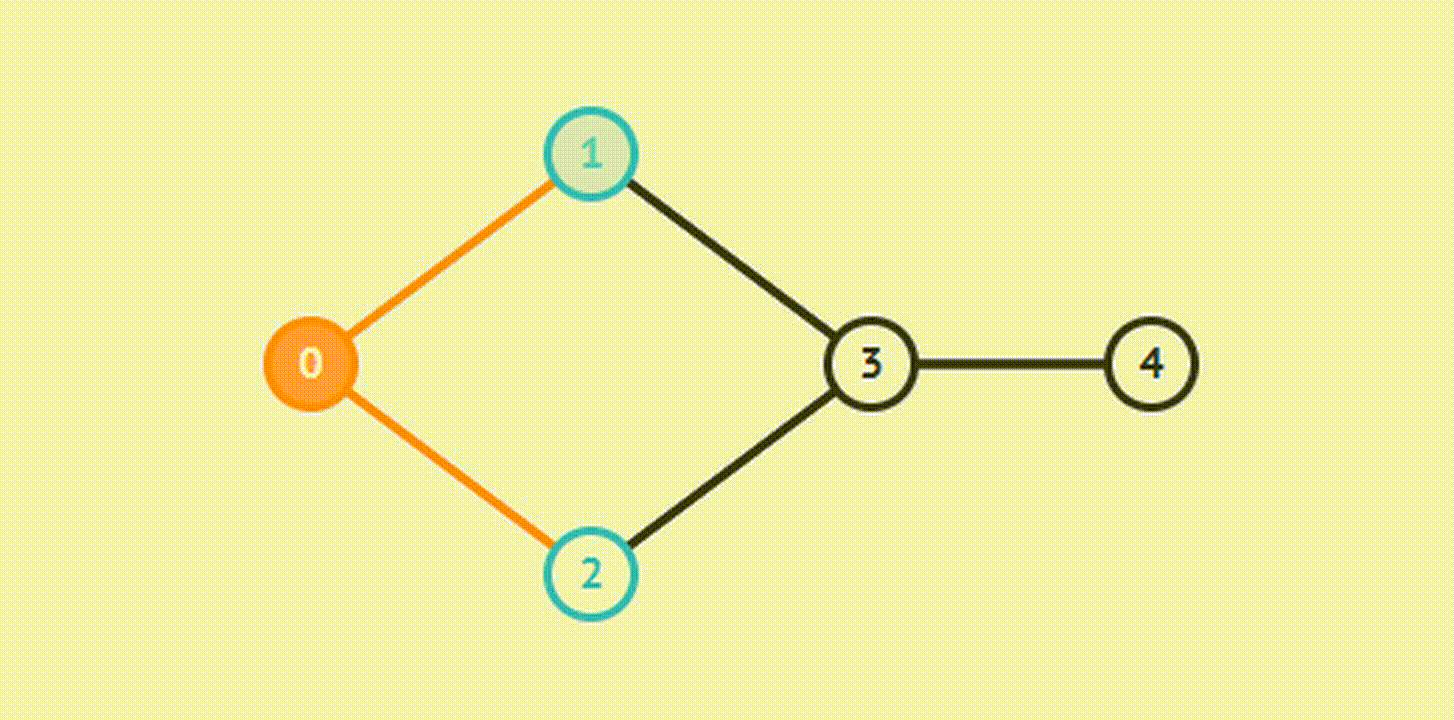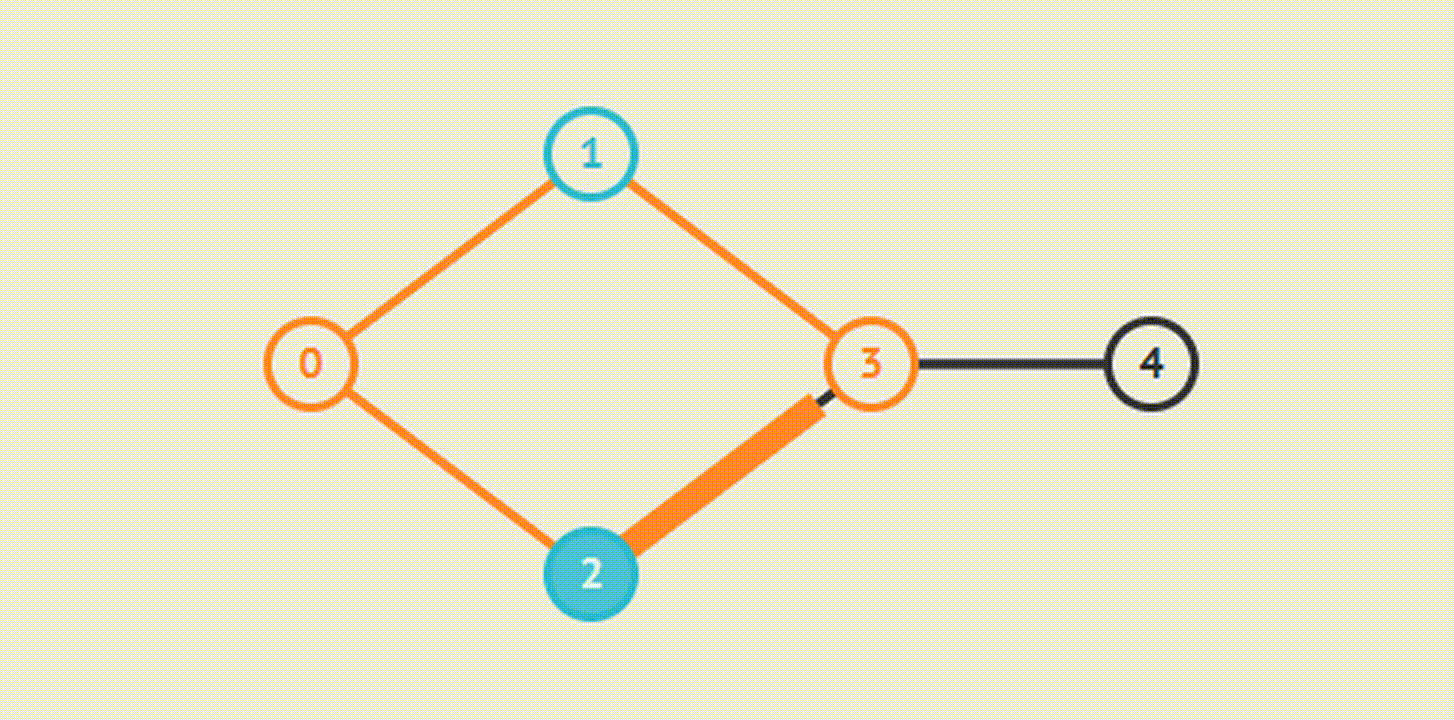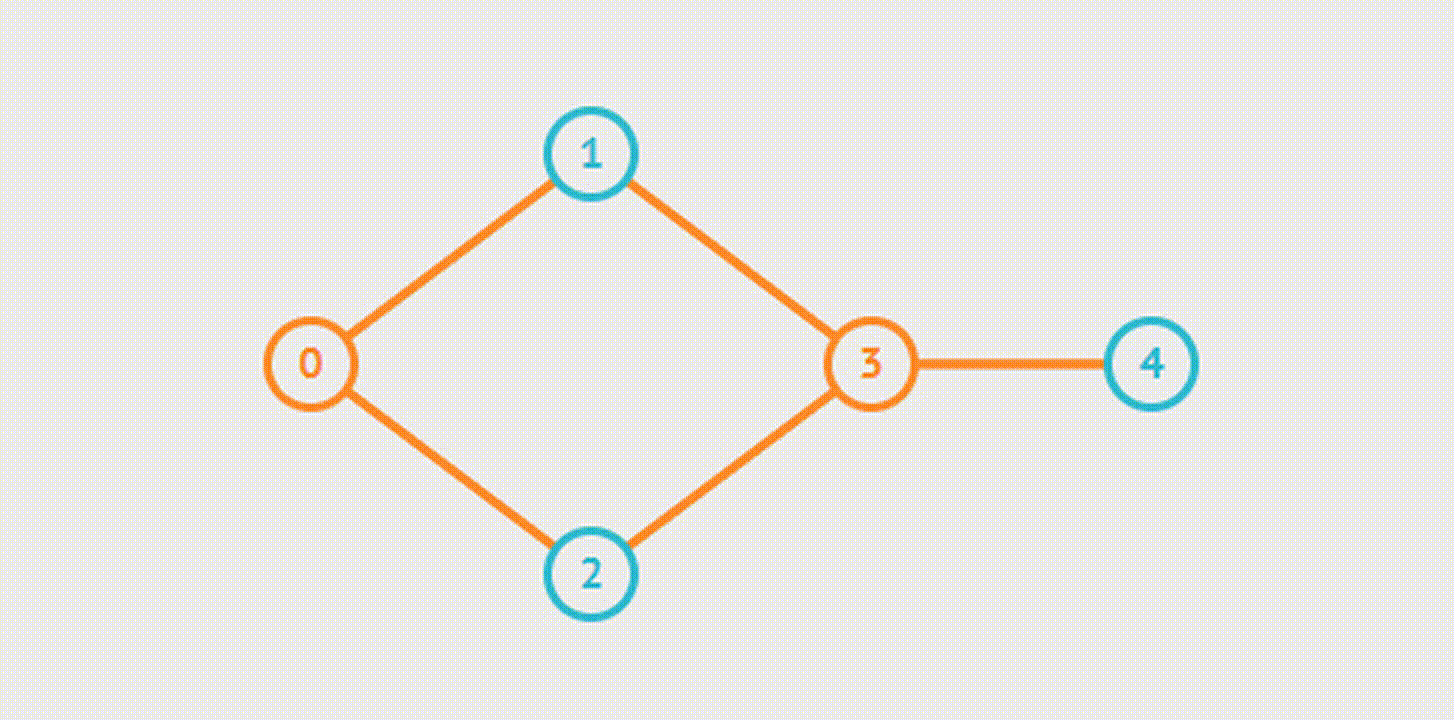
DFS

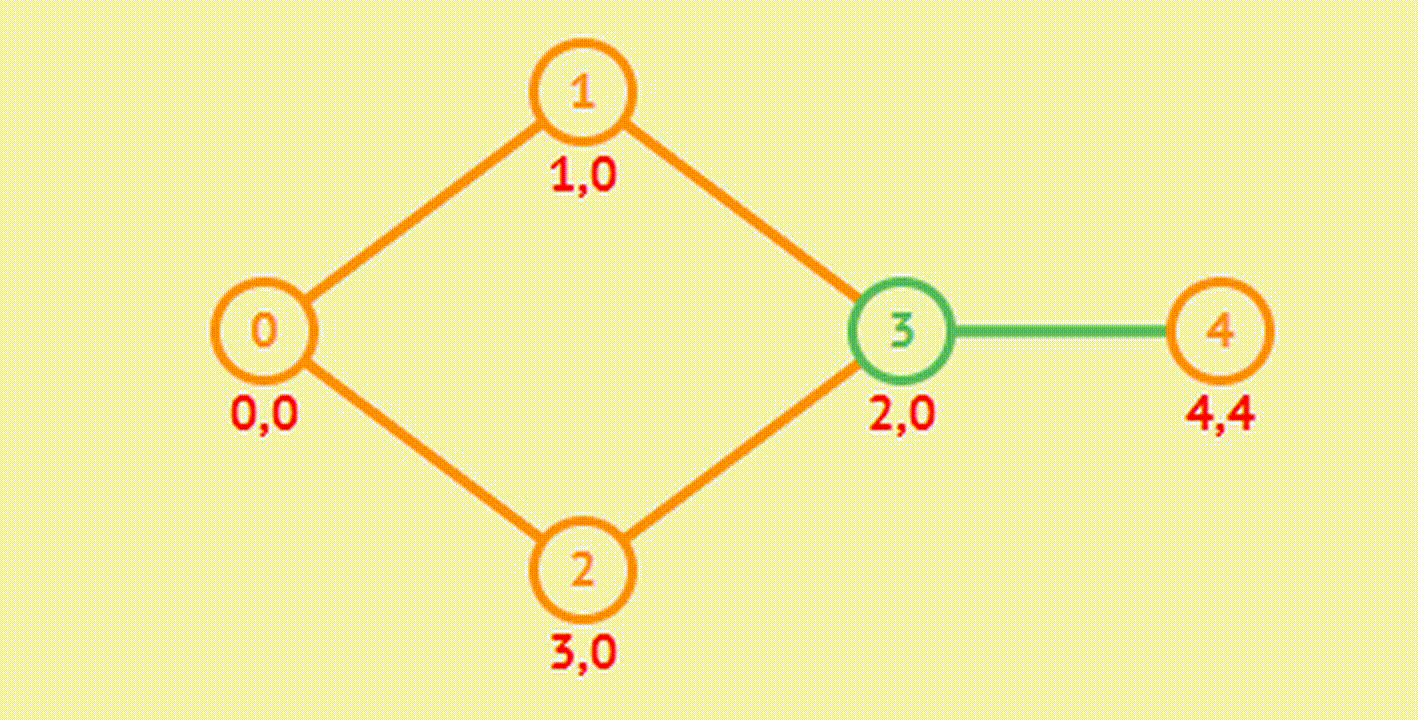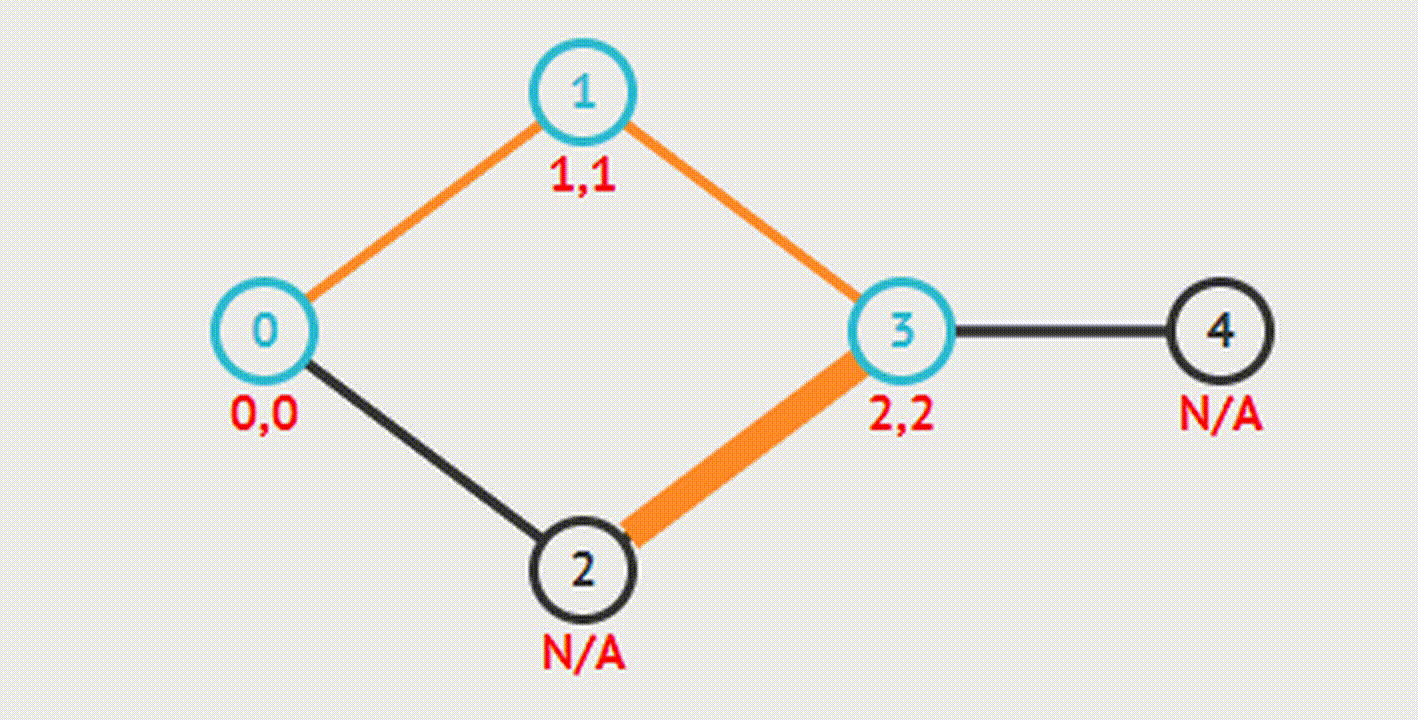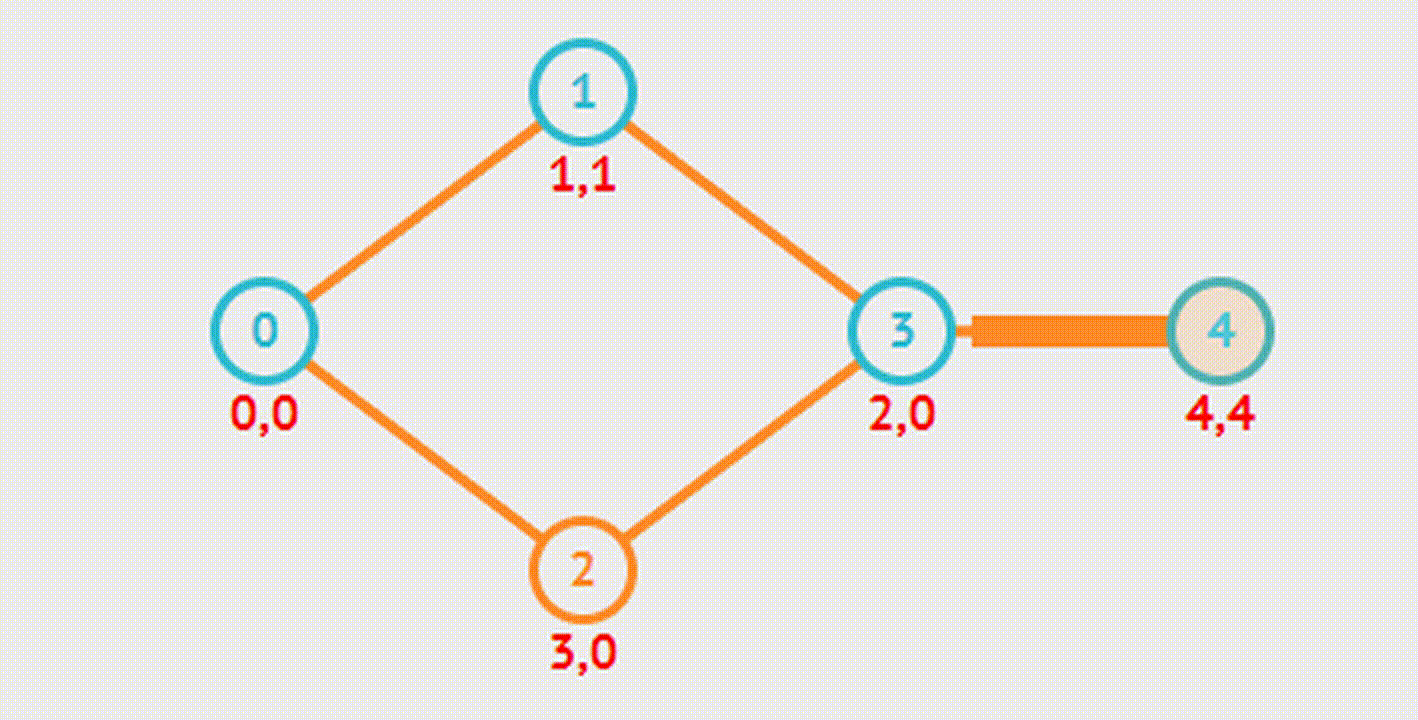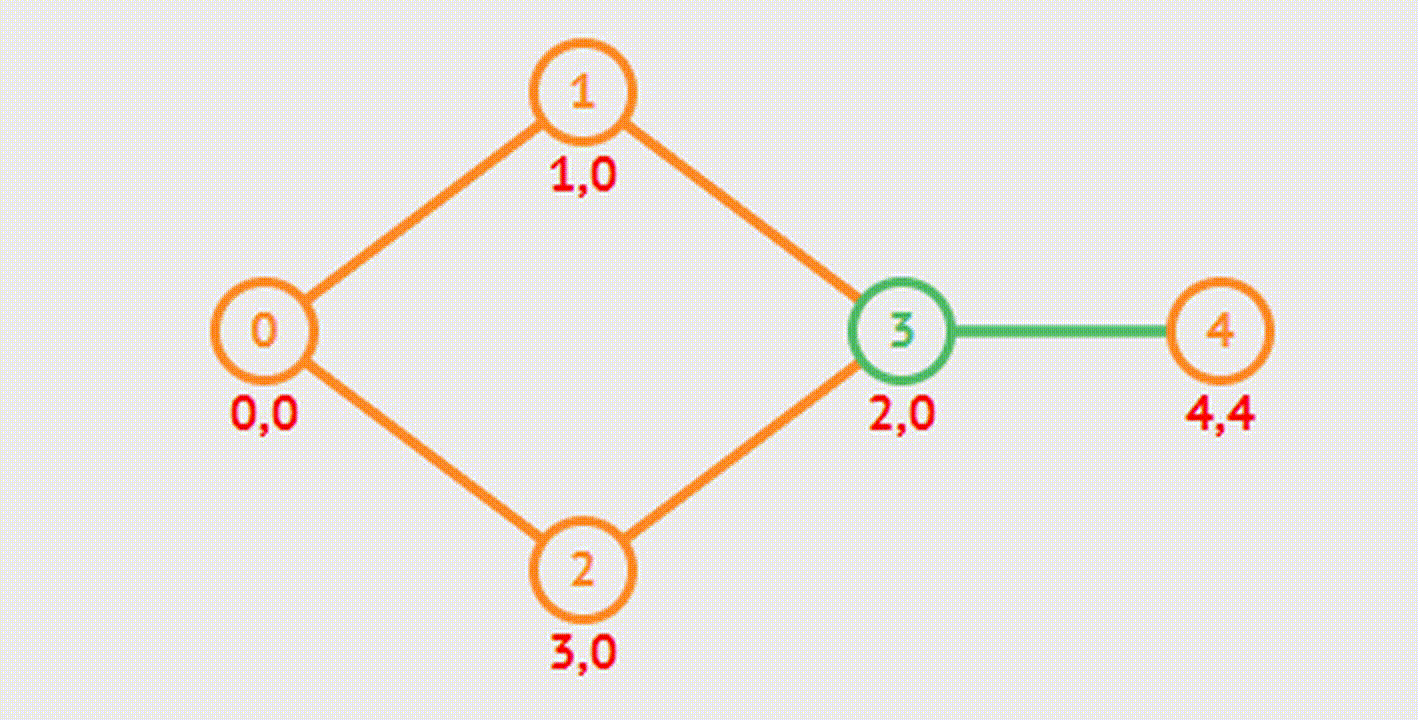
Cut Vertex & Bridge - Шарнир и Мост

Этот алгоритм используется для нахождения шарниров и мостов в графе.
Шарнир - точка, удаление которой делает граф несвязным.
Мост - ребро, удаление которого увеличивает число компонент связности.

Дополнительные материалы по теме

Сортировки в гифках: 8 самых популярных алгоритмов
Изучаем алгоритмы и структуры данных правильно
Какие алгоритмы нужно знать, чтобы стать хорошим программистом?