Пользователю polygenelubricants задали на собеседовании такой вопрос: «В мешке находятся числа 1, 2, 3…100. Каждое число появляется только один раз, поэтому чисел ровно 100. Предположим, одно число вынули из мешка. Как определить это число?»
Это очень популярная задача, и разработчик без труда ее решил: «Сумму последовательности 1 + 2 + 3 + … + N можно определить по формуле (N+1)(N/2). Для N = 100 сумма будет равна 5050. Если вычесть из 5050 сумму чисел, которые остались в мешке, разница будет равна отсутствующему числу».
bag = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26,
27, 28, 29, 30, 31, 32, 33, 34,
35, 36, 37, 38, 39, 40, 41, 42,
43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58,
59, 60, 61, 62, 63, 64, 65, 66,
67, 68, 69, 70, 71, 72, 73, 74,
75, 76, 77, 78, 79, 80, 81, 82,
83, 84, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99, 100] # отсутствует число 85
n = 100
missing_number = (n + 1) * (n / 2) - sum(bag)
print(int(missing_number)) # вывод = 85
Но радоваться было рано – коварный интервьюер задал следующий вопрос: «А как найти два отсутствующих числа»? Разработчик такого поворота событий не ожидал и запаниковал. Интервьюер пытался навести программиста на конструктивные размышления и намекнул, что есть подход для решения этой задачи, который:
- Включает несколько уравнений.
- Можно использовать для определения 2, 3, и даже k отсутствующих чисел.
- Обладает лучшей временной и пространственной сложностью, чем О(n), потому что зависит от k.
Несколько месяцев разработчик размышлял над максимально оптимальным решением этой задачи для 2, 3, k ≥ 4 чисел, и наконец создал тему на Stack Overflow. К этому моменту легких решений он уже не искал:
- Искомое решение должно работать не только для 100, но и для любого N чисел.
- Не должно использовать самые очевидные подходы – битовый массив и сортировку.
- Должно быть максимально универсальным, максимально эффективным, эдаким «Святым Граалем» всех возможных решений, даже если сложность реализации сделает этот подход непрактичным.
Два предложенных вариантa решения
Решений в теме много, но оптимальными являются только два. Одно из решений подходит для поиска пропущенных чисел в массиве или списке, второе можно использовать и для массива, и для потока данных.
Решение для массива
Этот элегантный алгоритм работает с линейной скоростью O(n) – чуть хуже, чем было нужно автору вопроса, – зато отличается универсальностью и полным отсутствием сложной математики:
import random
n = 11
k = 2
def find_k_missing(array, n):
if len(array) == n:
return []
if len(array) == 0:
return list(range(n))
array.extend([array[0]] * (n - len(array)))
for i in range(n):
while array[i] != array[array[i]]:
t = array[i]
array[i] = array[t]
array[t] = t
return [i for i in range(n) if array[i] != i]
array = list(range(n))
random.shuffle(array)
array = array[:n-k]
print(f'Заданный массив: {array}')
result = find_k_missing(array, n)
print(f'Найденные числа: {result}')
Решение для потока данных
Этот подход взят из книги об алгоритмах для поточной обработки данных, автор которой ссылается на алгоритм Мински-Трахтенберга-Зиппеля, представленный в 2003 году. Метод очень эффективен – работает за O(k2 log n), и одинаково хорошо подходит как для массивов фиксированного размера, так и для потоков данных. Недостаток у него только один – относительная сложность реализации, которую предвидел автор вопроса.
Алгоритм построен на использовании симметричных многочленов, для вычисления которых нужно использовать тождества Ньютона и числа Бернулли. Из этих многочленов составляют систему уравнений или полином k-степени – корни будут равны пропущенным числам. Как именно это делается – рассмотрим ниже.
Как быстро освоить математику?
Заглядывай на наш онлайн-курс по математике для Data Science, где ты познакомишься с основными моделями машинного обучения, научишься выбирать и применять подходящие tree-based модели.
Программа занятий:
- Школьная математика: от теории множеств до производной и интеграла.
- Математический анализ: от числовых последовательностей до теории меры и интеграла Ламбера.
- Линейная алгебра: от матриц до билинейных форм.
- Комбинаторика: правила комбинаторики, множества и сочетания.
- Теория вероятностей и математическая статистика: от случайных событий до регрессии.
- Машинное обучение: Word2vec, градиентный спуск, KNN и т. д.
«Святой Грааль»
Пользователи, которым почему-то не понравилось «математическое» решение, предложенное в исходной теме, продолжили обсуждение в форке. Однако обсуждение быстро зашло в тупик, и это неудивительно: как показывает профессор Мэрилендского университета в Колледж-Парке Уильям Гасарш в этой публикации (pdf), на сегодняшний день известны только два относительно простых (и при этом очень эффективных) подхода для вычисления k ≥ 4, и оба используют симметрические функции. При использовании первого подхода симметрические многочлены выражаются через степенные суммы с помощью тождеств Ньютона, а при втором функции применяются на всех этапах решения.
Как найти 1, 2, 3 и k ≥ 4 пропущенных чисел в массиве или потоке
В упомянутой выше публикации Гасарш приводит 2-3 варианта решения для каждого случая. Все решения описаны математически. Так, например, выглядит первый вариант решения для общего случая:
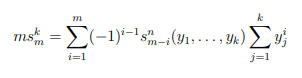
А это второй вариант:
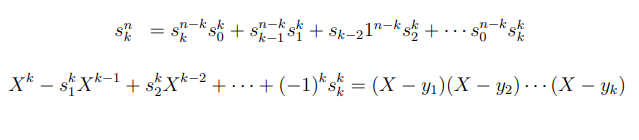
По представленным в публикации решениям несложно написать код. Рассмотрим несколько примеров.
Первый способ решения для k = 1:
def find_missing_number(nums):
n = len(nums) + k
expected_sum = n * (n + 1) / 2
actual_sum = sum(nums)
missing_number = (expected_sum - actual_sum) % n
return missing_number
nums = [10, 1, 4, 7, 2, 3, 5, 9, 8]
k = 1
missing_number = find_missing_number(nums)
print(f"Пропущенное число: {missing_number:.0f}")
Второй способ решения для k = 1 (с использованием XOR):
def find_missing_number(nums):
n = len(nums) + k
xor_sum = 0
for i in range(1, n + 1):
xor_sum ^= i
for num in nums:
xor_sum ^= num
return xor_sum
nums = [1, 10, 4, 7, 2, 3, 6, 9, 8]
k = 1
missing_number = find_missing_number(nums)
print(f"Пропущенное число: {missing_number}")
Решение для k = 2 с использование суммы квадратов:
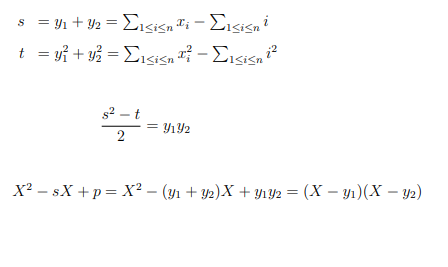
def calculate_s_and_t(data):
n = len(data) + k
s_complete = n * (n + 1) / 2
t_complete = n * (n + 1) * (2 * n + 1) / 6
s_incomplete = sum(data)
t_incomplete = sum(num**2 for num in data)
s = s_complete - s_incomplete
t = t_complete - t_incomplete
return s, t
def find_roots(s, t):
d = s**2 - 4 * ((s**2 - t) / 2)
if d >= 0:
root1 = (-s + (d) ** 0.5) / 2
root2 = (-s - (d) ** 0.5) / 2
return root1, root2
else:
print("Уравнение имеет комплексные корни.")
return None
data = [1, 2, 4, 6, 7, 8, 9, 10, 11, 12, 13]
k = 2
s, t = calculate_s_and_t(data)
roots = find_roots(s, t)
if roots:
print(f"Найдены пропущенные числа: {roots[0] * -1:.0f} и {roots[1]* -1:.0f}")
Решение для k = 3 с использованием тождеств Ньютона
Основные шаги:
- Вычисляем суммы степеней чисел от 1 до n, используя формулы суммирования степеней последовательных натуральных чисел. Это ожидаемые суммы степеней полного набора чисел.
- Вычисляем неполные суммы степеней для фактически имеющихся чисел в списке data.
- Находим разности между полными и неполными суммами степеней – это значения b1, b2, b3, которые представляют собой суммы соответствующих степеней недостающих чисел.
- Используя тождества Ньютона, из найденных сумм степеней восстанавливаем коэффициенты c1, c2, c3 многочлена третьей степени, корнями которого являются недостающие числа.
import numpy as np
def calculate(data):
n = len(data) + k
а1_complete = n * (n + 1) / 2
а2_complete = n * (n + 1) * (2 * n + 1) / 6
а3_complete = n**2 * (n + 1)**2 / 4
а1_incomplete = sum(data)
а2_incomplete = sum(num**2 for num in data)
а3_incomplete = sum(num**3 for num in data)
b1 = а1_complete - а1_incomplete
b2 = а2_complete - а2_incomplete
b3 = а3_complete - а3_incomplete
return b1, b2, b3
data = [1, 11, 2, 12, 4, 6, 13, 7, 8, 10]
k = 3
b1, b2, b3 = calculate(data)
c1 = b1
c2 = (b1**2 - b2) / 2
c3 = (b1**3 - 3*b1*b2 + 2*b3) / 6
# Коэффициенты полинома
coefficients = [1, c1, c2, c3]
# Вычисление корней (пропущенных чисел)
roots = np.roots(coefficients)
print(f"Сформировано кубическое уравнение: x**3 + {c1}x**2 + {c2}x + {c3}")
print(f"Найдены пропущенные числа: {roots[0] * -1:.0f}, {roots[1]* -1:.0f}, {roots[2]* -1:.0f}")
Как очевидно, при k > 3 (и при обработке больших массивов данных) нецелесообразно хардкодить формулы и держать все числа в памяти одновременно. Поэтому для k ≥ 4 и потоковой обработки данных используют другой подход, с рекуррентными формулами.
Общий случай
До сих пор для вычисления ожидаемых сумм степеней чисел мы использовали готовые формулы. Таких формул выведено немало, но по мере возрастания степени они становятся все более и более громоздкими:
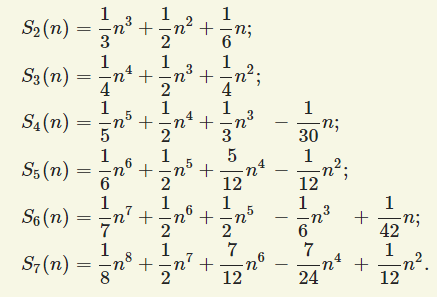
Однако существует и общая формула – ее вывел в конце 17 века Якоб Бернулли:
Здесь B – соответствующее число Бернулли:

Что же касается коэффициентов (симметрических многочленов), то они определяются с помощью тождеств Ньютона. В примерах выше мы уже использовали эти формулы:

Общая формула выглядит так:
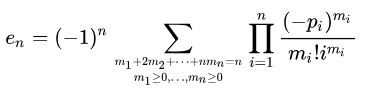
Как уже упоминалось выше, при обработке очень больших массивов данных целесообразнее использовать поточную вариацию алгоритма: тогда вычисления для входного потока данных можно делать рекуррентно, по мере поступления чисел, а вместо тождеств Ньютона использовать прямой подход к получению симметрических функций. Как реализовать этот алгоритм – разберем в следующей статье.




Комментарии