- Узлы – отдельные сущности или концепции предметной области. Например, «Альберт Эйнштейн», «Теория относительности», «Физика» и т. д.
- Ребра – связи между узлами, которые описывают отношения между сущностями. Например, «Альберт Эйнштейн» – «разработал» – «Теория относительности».
- Типы узлов и связей – позволяют категорировать сущности (персоны, концепции, места и т.д.) и отношения между ними (родственные, временные, иерархические и др.)
- Веса связей – числовые значения, указывающие на важность или релевантность связей между узлами.
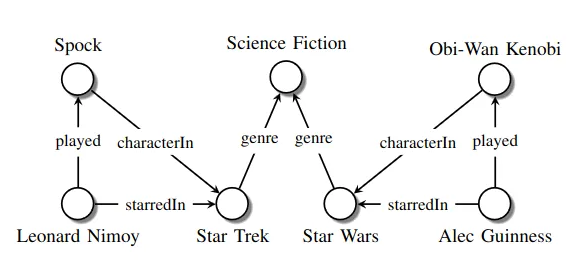
Графы знаний используются в поисковых системах, электронной коммерции, биоинформатике, научных исследованиях и многих других сферах, где требуется систематизация и анализ больших объемов структурированных и неструктурированных данных. С их помощью можно создать контекстную память для чат-бота, и это значительно улучшит качество его работы:
- Снизит уровень галлюцинаций.
- Повысит релевантность и точность ответов LLM.
- Даст модели возможность корректно обрабатывать данные, которых она не знает.
Подробный туториал показывает, как именно это сделать – на примере данных из Википедии и Gemini Pro. В этой публикации:
- Описывается процесс создания графа знаний путем анализа страниц Википедии, извлечения концепций, связей между ними и весов этих связей на основе статистики упоминаний на страницах.
- Приводится подробный код на Python для реализации этого процесса с использованием библиотек Wikipedia, Pandas, NetworkX и др.
- Демонстрируется визуализация полученного графа знаний.
- Показано, как интегрировать полученный граф знаний с LangChain для использования в качестве контекстной памяти для большой языковой модели Gemini-1.0-Pro от Google.

Не хочу читать статьи, хочу выучить высшую математику. Что делать?
Поднять уровень знаний на нашем курсе «математика для Data Science».
Вы научитесь решать задачи, которые дают на собеседованиях в компании размера FAANG. Курс также идеально подходит к поступлению в Школу анализа данных Яндекса. Программа разработана преподавателями ВМК МГУ, одного из лучших математических факультетов страны
Основные темы:
- Начала теории множеств.
- Геометрическая прогрессия. Векторы.
- Теория вероятностей. Рациональные уравнения.
- Алгебраические уравнения.
- Иррациональные уравнения. Графический способ решения систем.
- Неравенства.
- Функции, график и свойства.
- Графики функций и их преобразования.
- Производная, исследование функций.
- Исследование функций. Интеграл.




Комментарии