Данная публикация представляет собой сокращенный перевод руководства Мирко Стожилковича Hands-On Linear Programming: Optimization With Python. Для удобства читателей текст перевода также адаптирован в виде Jupyter-блокнота.
Линейное программирование – это набор методов, используемых в математическом программировании, также называемых математической оптимизацией. Эти методы используются для решения систем линейных уравнений и неравенств, перед которыми стоит цель максимизации или минимизации некоторой линейной функции. Линейное программирование используется в научных вычислениях, экономике, технических науках, производстве, транспорте, военном деле, логистике, энергетике и т. д.
Экосистема Python включает несколько мощных инструментов линейного программирования. Из этого руководства вы узнаете:
- что такое линейное программирование и в чем его польза;
- какие инструменты Python подходят для линейного программирования;
- как построить модель и решить задачу линейного программирования на Python.
Что собой представляет линейное программирование
Системы линейных уравнений и неравенств часто имеют множество возможных решений.
Линейное программирование – это набор математических и вычислительных инструментов, позволяющих найти конкретное решение системы, которое соответствует максимуму или минимуму какой-либо другой линейной функции. Линейное программирование – это фундаментальный метод оптимизации, десятилетиями применяемый в областях, требующих большого объема математических вычислений. Эти методы точны, сравнительно быстры и подходят для множества практических приложений.
Смешанно-целочисленное линейное программирование – это вид линейного программирования, которое фокусируется на обработке задач, где хотя бы одна переменная принимает дискретные целые, а не непрерывно меняющиеся значения.
Целочисленные переменные важны для правильного представления количеств, естественным образом выражаемых целыми числами, таких как число выпущенных самолетов или количество обслуженных клиентов.
Особенно важным видом целочисленных переменных являются бинарные переменные, имеющие лишь значения 0 или 1, и полезные при принятии решений вида «да»/«нет». Например, следует ли строить завод, включить или выключить машину. Также их можно использовать для имитации логических ограничений.
Смешанно-целочисленное линейное программирование позволяет преодолеть многие ограничения линейного программирования. Можно аппроксимировать нелинейные функции кусочно-линейными, использовать полунепрерывные переменные, логические ограничения модели. Это требовательный к ресурсам инструмент, но достижения в области компьютерного оборудования и программного обеспечения сделали его более доступным.
Линейное программирование на Python
Базовый метод решения задач линейного программирования называется симплекс-методом, другой популярный подход – метод внутренней точки. Задачи смешанного целочисленного линейного программирования решаются с помощью более сложных и ресурсоемких методов, таких как метод ветвей и границ.
Заметим, что почти все широко используемые библиотеки линейного программирования и смешанно-целочисленного линейного программирования написаны на языках Fortran, C или C++, так как линейное программирование требует интенсивной вычислительной работы с матрицами, часто очень большими. Соответствующие инструменты Python – это просто удобные интерфейсы для работы с низкоуровневыми библиотеками – солверами.
В этом руководстве для определения и решения задач линейного программирования мы будем использовать Python-библиотеки SciPy и PuLP.
1. Примеры задач линейного программирования
1.1. Небольшой показательный пример
Рассмотрим следующую задачу максимизации:
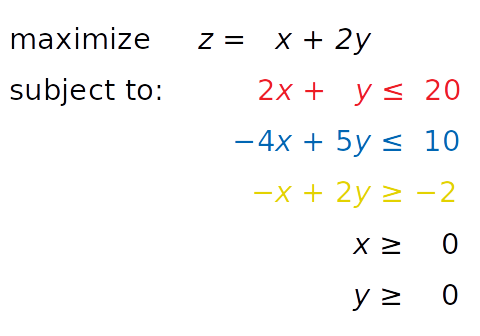
Нам нужно найти такие x и y, чтобы выполнялись «красное», «синее» и «желтое» неравенства, а также ограничения x ≥ 0 и y ≥ 0. При этом решение должно соответствовать максимально возможному значению z.
Независимые переменные, которые нужно найти (x и y) называют переменными решения (decision variables). Функция, которую необходимо максимизировать или минимизировать (z), – это целевая функция (objective function), функция стоимости (cost function) или просто цель (goal). Неравенства (или уравнения), которым необходимо удовлетворять, называются ограничениями (inequality constraints или equality constraints для обычных уравнений).
Проблему можно визуализировать следующим образом.
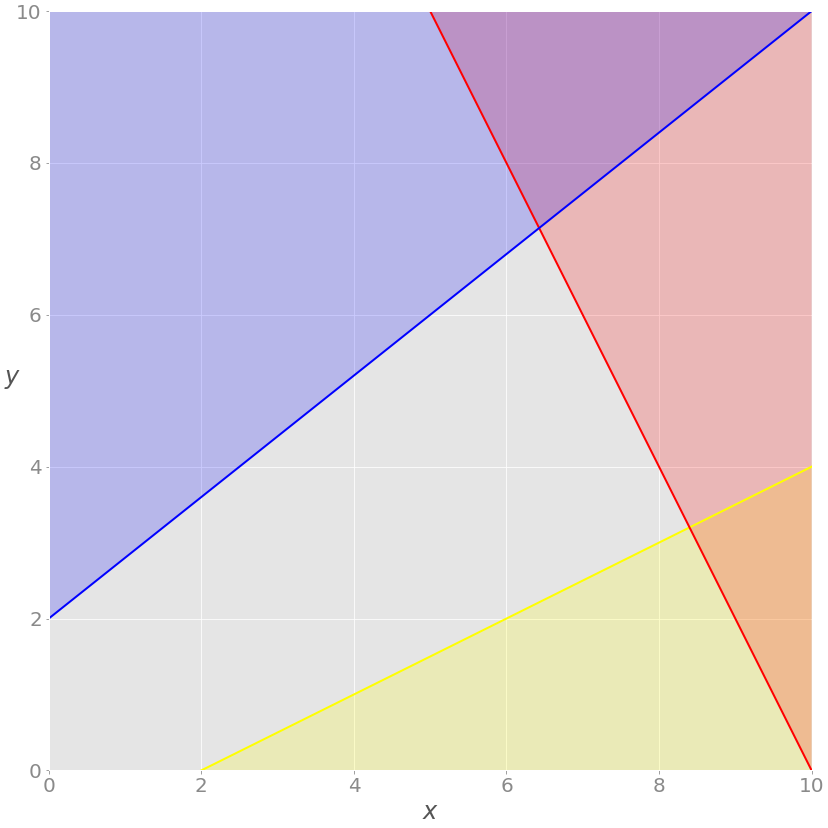
2x + y = 20, а красная область над ней показывает, где красное неравенство не выполняется. Аналогично синяя линия – это −4x + 5y = 10, желтая линия – это−x + 2y = −2, окрашенные области – та часть плоскости, где неравенство не выполняется.Каждая точка серой области удовлетворяет всем ограничениям и является потенциальным решением задачи. Эта область называется областью допустимых решений (feasible region), а ее точки – допустимыми решениями (feasible solutions).
Мы хотим максимизировать z. Решение, соответствующее максимальному значению z, называют оптимальным решением.
Обратите внимание, что функция z линейна. Оптимальное решение должно находиться в одной из вершин области допустимых решений. Иногда весь край допустимой области или даже вся область может соответствовать одному и тому же значению z.
Представим, что в задачу введено дополнительное ограничение в виде равенства, окрашенного зеленым:
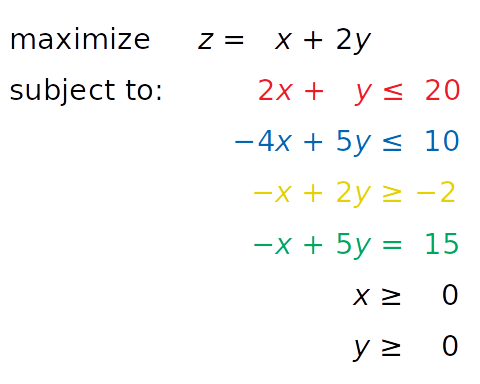
Его можно визуализировать, добавив соответствующую зеленую прямую:
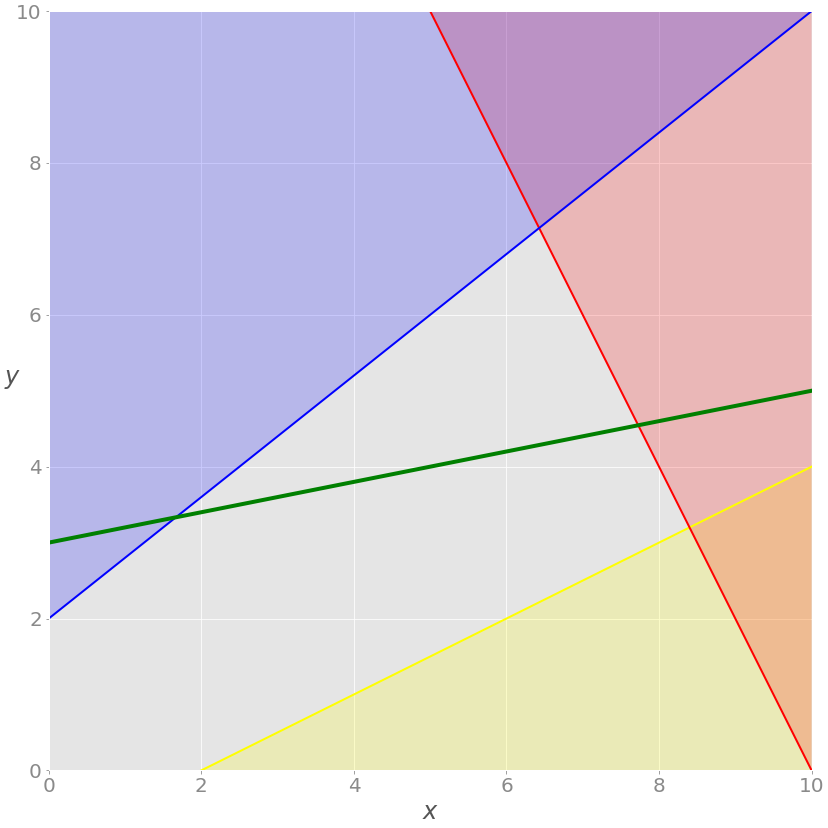
Теперь область допустимых решений не соответствует всей серой зоне. Это лишь часть зеленой линии, проходящей через серую область от точки пересечения с синей линией до точки пересечения с красной.
Если добавить требование, что все значения x должны быть целыми числами, то мы получим задачу смешанно-целочисленного линейного программирования, и набор возможных решений снова изменится:
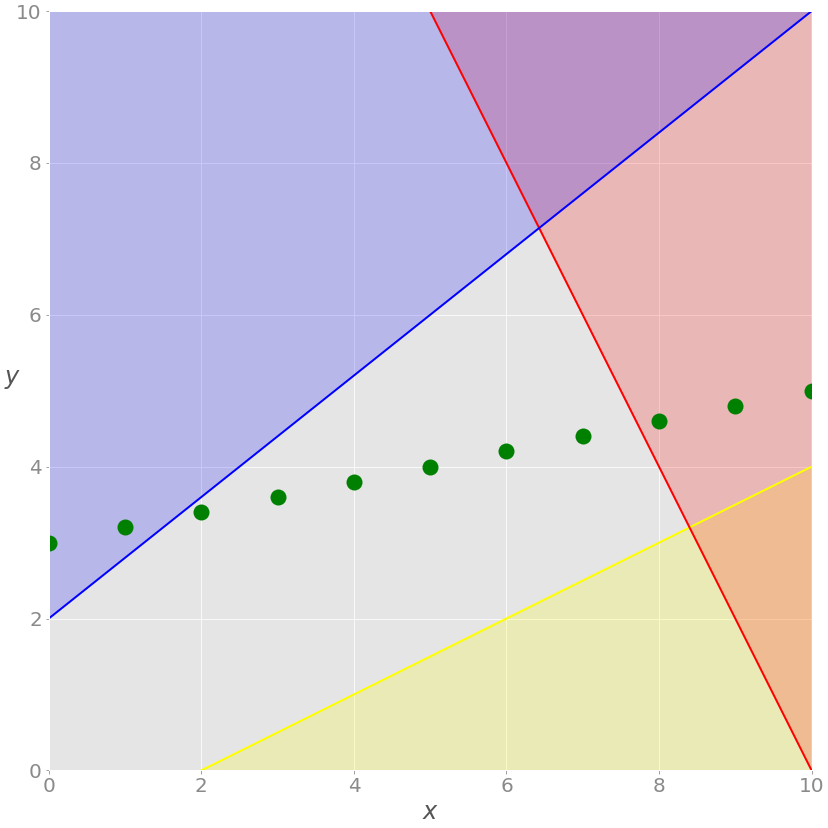
Больше нет зеленой линии – только дискретные точки, где значение x является целым числом. Возможные решения – это зеленые точки на сером фоне.
Эти три примера иллюстрируют задачи линейного программирования – они имеют ограниченные допустимые области решений и конечные решения.
Когда ни одно решение не может удовлетворить все ограничения сразу, задача в рамках линейного программирования неразрешима.
1.2. Задача о распределении ресурсов
В предыдущих разделах мы рассмотрели абстрактную задачу линейного программирования, не связанную с каким-либо реальным приложением. В этом разделе речь пойдет о более практической задачи оптимизации, связанной с распределением ресурсов на производстве.
Предположим, что фабрика производит четыре различных продукта, ежедневное количество первого продукта составляет x_1, второго продукта – x_2 и т. д. Цель – определить максимальную прибыль ежедневного объема производства для каждого продукта с учетом следующих условий:
- Прибыль (profit) на единицу продукта составляет 20, 12, 40 и 25 долларов для каждого из четырех продуктов соответственно.
- Из-за нехватки рабочей силы (manpower) общее количество единиц, производимых в день, не может превышать 50.
- На каждую единицу 1-го продукта расходуется 3 единицы сырья A. Каждая единица 2-го продукта требует 2 единиц сырья A и 1 единицы сырья B. Каждой единице 3-го продукта требуется 1 единица A и 2 единицы B. Наконец, каждая единица 4-го продукта требует трех единиц. B.
- Из-за ограничений по транспортировке и хранению фабрика может потреблять до 100 единиц сырья A и 90 единиц B в день.
Математическую модель можно определить так:
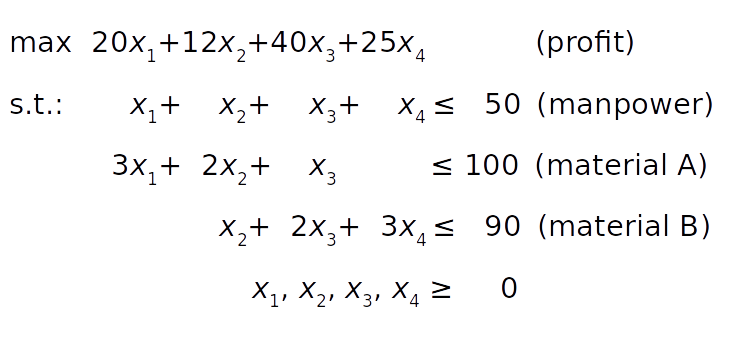
Целевая функция (прибыль) определяется в условии 1. Ограничение рабочей силы следует из условия 2. Ограничения на сырье A и B могут быть получены из условий 3 и 4 путем суммирования потребностей в сырье для каждого продукта. Наконец, количество продуктов не может быть отрицательным.
В отличие от предыдущего примера, эту задачу не так удобно визуализировать, потому как она имеет четыре переменных. Однако принципы остаются теми же.
2. Линейное программирование на Python. Практическая реализация
В этом руководстве мы будем использовать для решения описанной выше задачи линейного программирования два пакета Python :
SciPy– универсальный пакет для научных вычислений с Python. Его внутренний пакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.PuLP– API линейного программирования Python для определения задачи и вызова солверов. По умолчанию в качестве солвера используется COIN-OR Branch and Cut Solver (CBC). Еще один отличный солвер с открытым исходным кодом – GNU Linear Programming Kit (GLPK).
2.1. Установка SciPy и PuLP
Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP.
python -m pip install -U scipy pulp
Возможно, вам потребуется запустить pulptest или sudo pulptest, чтобы включить солверы PuLP, особенно если вы используете Linux или Mac:
pulptest
2.2. Использование SciPy
В этом разделе мы рассмотрим, как использовать библиотеку SciPy по оптимизации и поиску корней для линейного программирования. Начнём с импорта scipy.optimize.linprog():
from scipy.optimize import linprog
2.3. Решение первого примера c помощью SciPy
Начнём с решения первого (дополненного) примера:
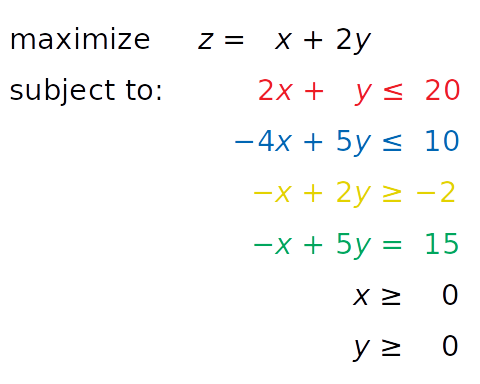
linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений-неравенств со знаком больше или равно (≥). Чтобы обойти эти проблемы, нам необходимо изменить описание задачи перед запуском оптимизации:
- Вместо максимизации
z = x + 2yминимизируем отрицательное значение (−z = −x − 2y). - Вместо знака
≥мы можем умножить «желтое» неравенство на-1и получить противоположный знак (ограничения по осям рассмотрим далее).
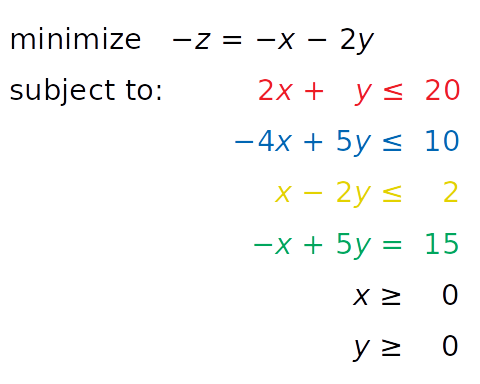
На следующем шаге определяем входные значения:
obj = [-1, -2]
# ─┬ ─┬
# │ └┤ Коэффициент для y
# └────┤ Коэффициент для x
lhs_ineq = [[ 2, 1], # левая сторона красного неравенства
[-4, 5], # левая сторона синего неравенства
[ 1, -2]] # левая сторона желтого неравенства
rhs_ineq = [20, # правая сторона красного неравенства
10, # правая сторона синего неравенства
2] # правая сторона желтого неравенства
lhs_eq = [[-1, 5]] # левая сторона зеленого равенства
rhs_eq = [15] # правая сторона зеленого равенства
Мы поместили значения из системы в соответствующие списки:
objсодержит коэффициенты целевой функции,lhs_ineqиrhs_ineqсодержат коэффициенты из ограничений-неравенств,lhs_eqиrhs_eqсодержат коэффициенты из ограничивающего уравнения.
Следующим шагом является определение границ каждой переменной. В данном случае они находятся между нулем и положительной бесконечностью:
bnd = [(0, float("inf")), # Границы x
(0, float("inf"))] # Границы y
Однако эти границы совпадают с установленными по умолчанию в linprog().
Наконец, пришло время оптимизировать и решить интересующую нас проблему:
opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq,
A_eq=lhs_eq, b_eq=rhs_eq, bounds=bnd,
method="revised simplex")
opt
con: array([0.])
fun: -16.818181818181817
message: 'Optimization terminated successfully.'
nit: 3
slack: array([ 0. , 18.18181818, 3.36363636])
status: 0
success: True
x: array([7.72727273, 4.54545455])
Параметр c относится к коэффициентам из целевой функции. A_ub и b_ub соответственно связаны с коэффициентами из левой и правой частей ограничений-неравенств. Точно так же A_eq и b_eq относятся к ограничениям уравнений. Параметр bounds служит для указания нижней и верхней границ переменных решения.
Параметр method определяет используемый алгоритм линейного программирования. Доступны три варианта:
- по умолчанию используется метод внутренней точки: method = "inner-point",
- измененный двухфазный симплекс-метод method="revised simplex",
- симплекс-метод method="simplex"
linprog() возвращает структуру данных со следующими атрибутами:
.con– остатки ограничения-равенства;.fun– оптимальное значение целевой функции (если найдено);.message– словесный статус решения;.nit– количество итераций, необходимых для завершения расчета;.slack– значения так называемых дополнительных переменных – разниц между значениями левой и правой сторонами ограничений;.status– целое число от 0 до 4, отражающих результат решения: например, 0, когда было найдено оптимальное решение;.success– логическое значение, показывающее, найдено ли оптимальное решение;.x– массив NumPy, содержащий оптимальные значения переменных решения.
Доступ к атрибутам можно получить по отдельности:
>>> opt.fun
-16.818181818181817
>>> opt.success
True
>>> opt.x
array([7.72727273, 4.54545455])
Графически результат можно отобразить следующим образом.
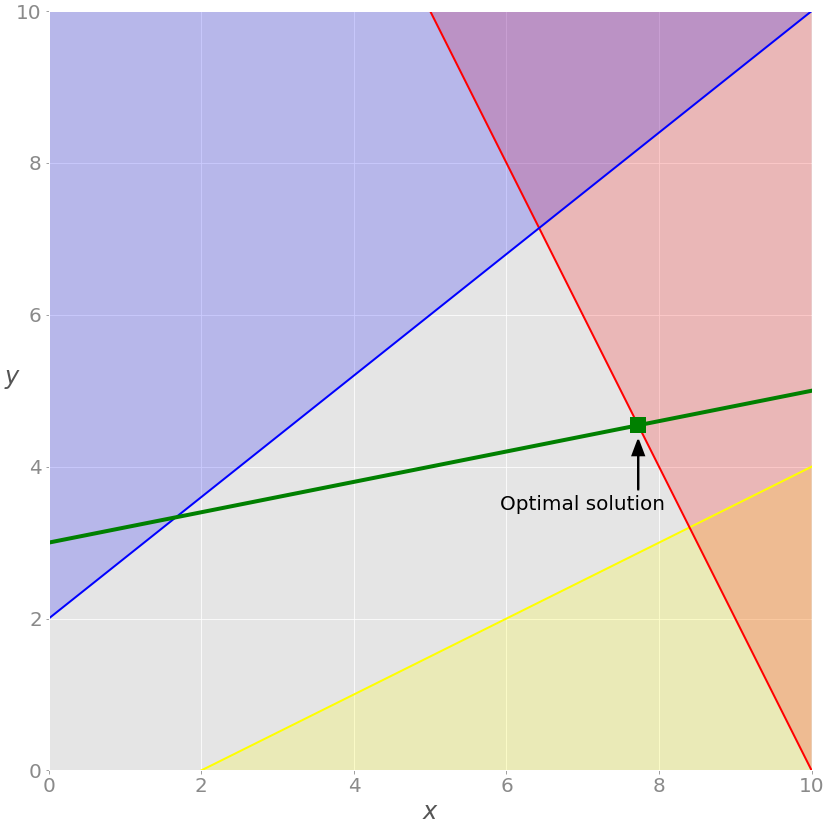
Вначале наша задача органичивалась только неравенствами. Если удалить параметры зеленого уравнения A_eq и b_eq из вызова linprog(), получим следующий результат:
opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq, bounds=bnd,
method="revised simplex")
opt
con: array([], dtype=float64)
fun: -20.714285714285715
message: 'Optimization terminated successfully.'
nit: 2
slack: array([0. , 0. , 9.85714286])
status: 0
success: True
x: array([6.42857143, 7.14285714])
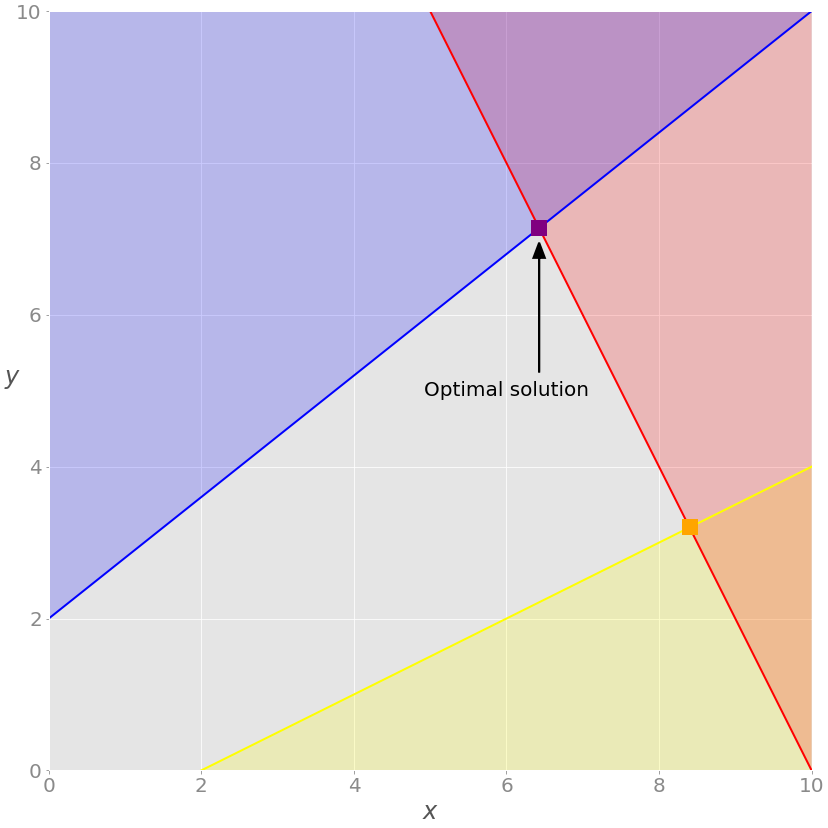
2.4. Решение задачи о производстве с помощью SciPy
Рассмотрим теперь решение второй задачи – о продуктах, рабочей силе и используемом сырье.
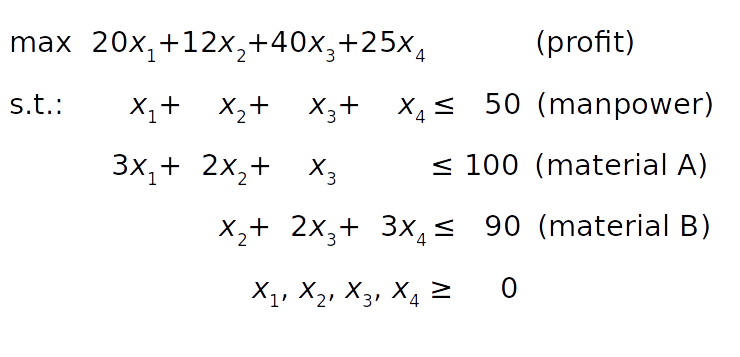
Как и в предыдущем примере, нам нужно извлечь необходимые векторы и матрицу из задачи, передать их в качестве аргументов в linprog():
obj = [-20, -12, -40, -25]
lhs_ineq = [[1, 1, 1, 1], # Рабочая сила
[3, 2, 1, 0], # Материал A
[0, 1, 2, 3]] # Материал B
rhs_ineq = [ 50, # Рабочая сила
100, # Материал A
90] # Материал B
opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq,
method="revised simplex")
opt
con: array([], dtype=float64)
fun: -1900.0
message: 'Optimization terminated successfully.'
nit: 2
slack: array([ 0., 40., 0.])
status: 0
success: True
x: array([ 5., 0., 45., 0.])
Максимальная прибыль составляет 1900 и соответствует x_1 = 5 и x_3 = 45. В данных условиях производить второй и четвертый продукты невыгодно. Результат позволяет сделать несколько интересных выводов:
- Третий продукт приносит наибольшую прибыль.
- Первая дополнительная переменная (
slack) равна 0. Это означает, что равны значения левой и правой сторон ограничения для рабочей силы. Завод производит 50 единиц в день, и это его полная мощность. - Вторая дополнительная переменная равна 40: фабрика потребляет 60 единиц сырья A (15 единиц для первого продукта и 45 для третьего) из возможных 100 единиц.
- Третья дополнительная переменная равен 0: фабрика потребляет все 90 единиц сырья B. При этом все это количество потребляется для производства третьего продукта. Вот почему фабрика вообще не может производить второй или четвертый товар и не может произвести более 45 единиц третьего товара. Cырья B просто не хватает.
Возможности линейного программирования SciPy полезны в основном для небольших задач. Для более крупных и сложных проблем разумно использовать другие библиотеки:
- SciPy не поддерживает работу с целочисленными переменными решения.
- SciPy не подразумевает запуск внешних солверов.
- SciPy не предоставляет классы или функции для построения моделей. Определять массивы и матрицы вручную для крупных задач слишком утомительно.
- Также вручную приходится переопределять задачи, как мы это сделали выше.
2.5. Решение первой задачи на линейное программирование с помощью PuLP
Итак, PuLP имеет более удобный API линейного программирования, чем SciPy. Начнем с импорта.
from pulp import LpMaximize, LpProblem, LpStatus, lpSum, LpVariable
Первый шаг – инициализировать экземпляр LpProblem для описания модели:
model = LpProblem(name="small-problem", sense=LpMaximize)
Параметр sense определяет, решаем ли мы задачу минимизации (параметр LpMinimize или 1, установлен по умолчанию) или максимизации (LpMaximize или -1).
Создав модель, мы можем определить переменные решения как экземпляры класса LpVariable:
x = LpVariable(name="x", lowBound=0)
y = LpVariable(name="y", lowBound=0)
Значения границ по умолчанию – отрицательная и положительная бесконечности, поэтому в нашем случае необходимо указать нижнюю границу (lowBound = 0).
Необязательный параметр cat определяет категорию переменной решения. При работе с непрерывными переменными можно использовать значение по умолчанию "Continuous".
Переменные x и y теперь можно использовать для создания других PuLP-объектов, представляющих линейные выражения и ограничения:
expression = 2 * x + 4 * y
print(type(expression))
constraint = 2 * x + 4 * y >= 8
print(type(constraint))
<class 'pulp.pulp.LpAffineExpression'>
<class 'pulp.pulp.LpConstraint'>
Построив линейную комбинацию нескольких переменных решения, мы получаем экземпляр pulp.LpAffineExpression, представляющий линейное выражение. Выражения можно комбинировать с операторами ==, <= и >= и получать экземпляры pulp.LpConstraint – линейные ограничения вашей модели.
Опишем теперь ограничения. В отличие от SciPy, с PuLP не нужно создавать списки и матрицы. Просто записываем выражения Python и добавляем в модель с помощью оператора +=:
model += (2 * x + y <= 20, "red_constraint")
model += (4 * x - 5 * y >= -10, "blue_constraint")
model += (-x + 2 * y >= -2, "yellow_constraint")
model += (-x + 5 * y == 15, "green_constraint")
LpProblem позволяет добавлять ограничения в модель, определяя их как кортежи. Первый элемент кортежа – экземпляр LpConstraint, второй – его удобочитаемое имя.
Аналогично описывается целевая функция:
obj_func = x + 2 * y
model += obj_func
Теперь можно посмотреть полное определение модели:
>>> model
small-problem:
MAXIMIZE
1*x + 2*y + 0
SUBJECT TO
red_constraint: 2 x + y <= 20
blue_constraint: 4 x - 5 y >= -10
yellow_constraint: - x + 2 y >= -2
green_constraint: - x + 5 y = 15
VARIABLES
x Continuous
y Continuous
Строковое представление модели содержит все соответствующие данные: цель, переменные, ограничения и их имена.
Теперь мы готовы решить задачу. Достаточно лишь вызвать метод .solve() для объекта модели.
status = model.solve()
Метод .solve() вызывает базовый солвер, изменяет объект модели и возвращает целочисленный статус решения, равный 1, если найден оптимум. Остальные коды состояний описаны в документации.
Результаты оптимизации доступны в виде атрибутов модели:
print(f"status: {model.status}, {LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")
status: 1, Optimal
objective: 16.8181817
x: 7.7272727
y: 4.5454545
red_constraint: -9.99999993922529e-08
blue_constraint: 18.181818300000003
yellow_constraint: 3.3636362999999996
green_constraint: -2.0000000233721948e-07
model.objective содержит значение целевой функции, model.constraints – значения дополнительных переменных, а объекты x и y имеют оптимальные значения переменных решения.
Результаты получились примерно такие же, как у SciPy.
Чтобы получить смешанно-целочисленное решение, достаточно обозначить это при помощи параметра cat:
# Создаем модель
model = LpProblem(name="small-problem", sense=LpMaximize)
# Инициализируем переменные решения: x - целое число, y меняется непрерывно
x = LpVariable(name="x", lowBound=0, cat="Integer")
y = LpVariable(name="y", lowBound=0)
# Добавляем ограничения
model += (2 * x + y <= 20, "red_constraint")
model += (4 * x - 5 * y >= -10, "blue_constraint")
model += (-x + 2 * y >= -2, "yellow_constraint")
model += (-x + 5 * y == 15, "green_constraint")
# Добавляем целевую функцию
# Вариант добавления через lpSum
model += lpSum([x, 2 * y])
# Решаем задачу оптимизации
status = model.solve()
print(f"status: {model.status}, {LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")
status: 1, Optimal
objective: 15.8
x: 7.0
y: 4.4
red_constraint: -1.5999999999999996
blue_constraint: 16.0
yellow_constraint: 3.8000000000000007
green_constraint: 0.0
Теперь x – целое число, как указано в модели. Этот факт меняет решение. Покажем это на графике:
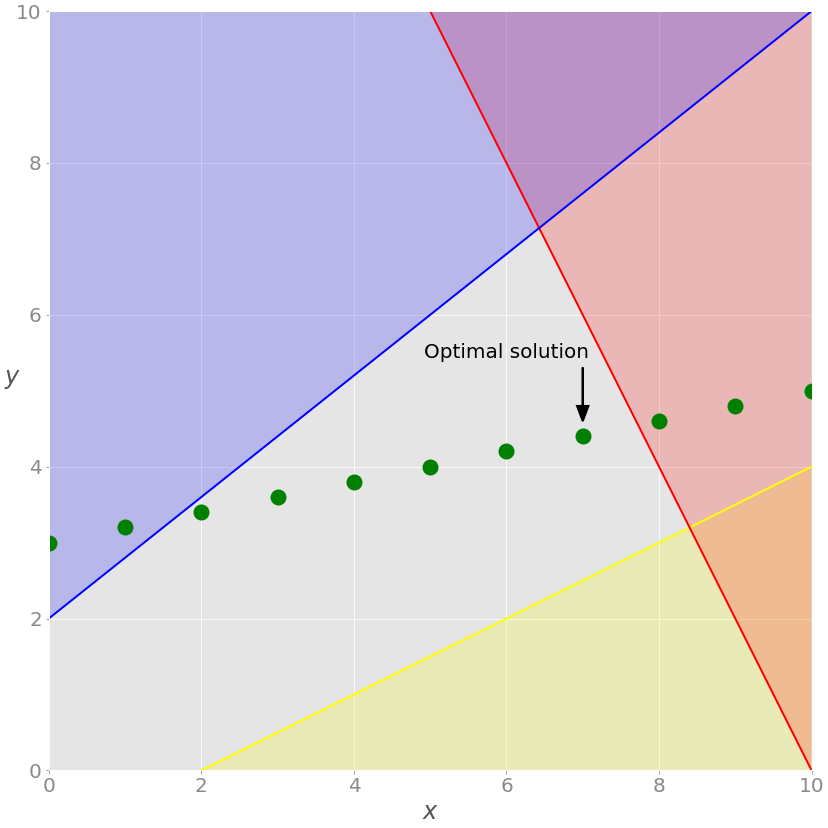
Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне. Это решение с наибольшими значениями как x, так и y, дающее максимальное значение целевой функции.
2.6. Решение задачи о производстве с помощью PuLP
Подход к определению и решению второй задачи такой же, как и в предыдущем примере:
# Определяем модель
model = LpProblem(name="resource-allocation", sense=LpMaximize)
# Описываем переменные
x = {i: LpVariable(name=f"x{i}", lowBound=0) for i in range(1, 5)}
# Добавляем ограничения
model += (lpSum(x.values()) <= 50, "manpower")
model += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
model += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "material_b")
# Описываем цель
model += 20 * x[1] + 12 * x[2] + 40 * x[3] + 25 * x[4]
# Решаем задачу оптимизации
status = model.solve()
# Выводим результаты решения
print(f"status: {model.status}, {LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in x.values():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")
status: 1, Optimal
objective: 1900.0
x1: 5.0
x2: 0.0
x3: 45.0
x4: 0.0
manpower: 0.0
material_a: -40.0
material_b: 0.0
Как видите, решение согласуется с тем, что мы молучили с помощью SciPy. Наиболее выгодное решение – производить в день 5 единиц первого продукта и 45 единиц третьего.
Давайте сделаем задачу более интересной. Допустим, из-за проблем с оборудованием, фабрика не может производить первую и третью продукцию параллельно. Какое решение наиболее выгодно в этом случае?
Теперь у нас есть еще одно логическое ограничение: если x_1 положительно, то x_3 должно равняться нулю, и наоборот. Здесь пригодятся бинарные переменные решения. Введем две переменные y_1 и y_3, которые будут обозначать, генерируются ли вообще первый или третий продукты:
model = LpProblem(name="resource-allocation", sense=LpMaximize)
x = {i: LpVariable(name=f"x{i}", lowBound=0) for i in range(1, 5)}
y = {i: LpVariable(name=f"y{i}", cat="Binary") for i in (1, 3)}
model += (lpSum(x.values()) <= 50, "manpower")
model += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
model += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "material_b")
M = 100
model += (x[1] <= y[1] * M, "x1_constraint")
model += (x[3] <= y[3] * M, "x3_constraint")
model += (y[1] + y[3] <= 1, "y_constraint")
model += 20 * x[1] + 12 * x[2] + 40 * x[3] + 25 * x[4]
status = model.solve()
print(f"status: {model.status}, {LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")
status: 1, Optimal
objective: 1800.0
x1: 0.0
x2: 0.0
x3: 45.0
x4: 0.0
y1: 0.0
y3: 1.0
manpower: -5.0
material_a: -55.0
material_b: 0.0
x1_constraint: 0.0
x3_constraint: -55.0
y_constraint: 0.0
При таких условиях оказывается, что оптимальный подход – исключить первый продукт вовсе и производить только третий.
Заключение
Теперь вы в общих чертах представляете, с какими задачами имеет дело линейное программирование и как использовать Python для решения подобных задач.
Теперь – после прохождения этого руководства – вы умеете:
- определить модель, которая описывает задачу в SciPy и PuLP;
- создать программу Python для оптимизационной задачи;
- запустить программу оптимизации, чтобы найти решение задачи;
- получить результат оптимизации.
Если вы хотите узнать больше о линейном программировании, вот несколько отправных точек, с которых можно начать:
- русскоязычная и анлоязычная вики-страницы о линейном программировании;
- русскоязычная и англоязычная вики-страницы о целочисленном программировании;
- туториал на Brilliant.org;
- вводный курс MIT о математическом программировании.
Следите за нашими тегами Python и Математика!




А как вы использовали линейное программирование?