Цепь Маркова – череда событий, в которой каждое последующее событие зависит от предыдущего. В статье мы подробнее разберём это понятие.
Цепь Маркова – это распространенный и довольно простой способ моделирования случайных событий. Используется в самых разных областях, начиная генерацией текста и заканчивая финансовым моделированием. Самым известным примером является SubredditSimulator. В данном случае Цепь Маркова используется для автоматизации создания контента во всем subreddit.
Цепь Маркова понятна и проста в использовании, т. к. она может быть реализована без использования каких-либо статистических или математических концепций. Цепь Маркова идеально подходит для изучения вероятностного моделирования и Data Science.
Сценарий
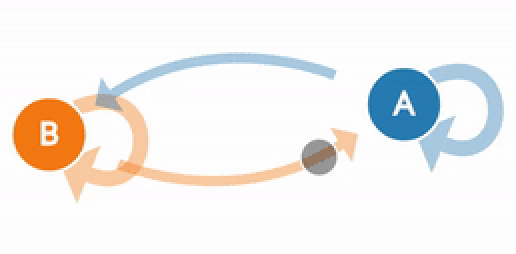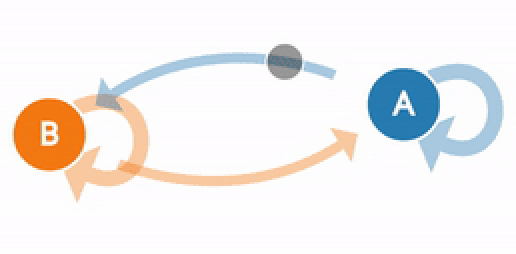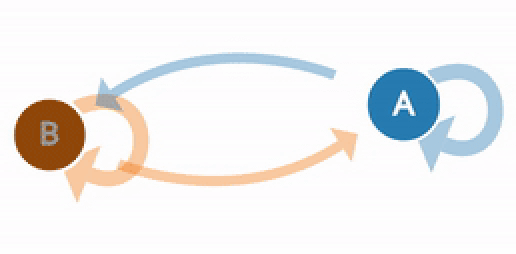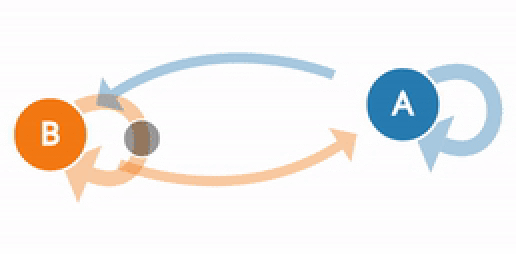
Представьте, что существует только два погодных условия: может быть либо солнечно, либо пасмурно. Всегда можно безошибочно определить погоду в текущий момент. Гарантированно будет ясно или облачно.
Теперь вам захотелось научиться предсказывать погоду на завтрашний день. Интуитивно вы понимаете, что погода не может кардинально поменяться за один день. На это влияет множество факторов. Завтрашняя погода напрямую зависит от текущей и т. д. Таким образом, для того чтобы предсказывать погоду, вы на протяжении нескольких лет собираете данные и приходите к выводу, что после пасмурного дня вероятность солнечного равна 0,25. Логично предположить, что вероятность двух пасмурных дней подряд равна 0,75, так как мы имеем всего два возможных погодных условия.
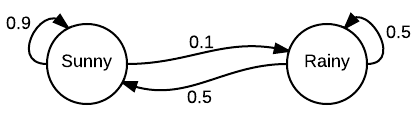
Теперь вы можете прогнозировать погоду на несколько дней вперед, основываясь на текущей погоде.
Этот пример показывает ключевые понятия цепи Маркова. Цепь Маркова состоит из набора переходов, которые определяются распределением вероятностей, которые в свою очередь удовлетворяют Марковскому свойству.
Обратите внимание, что в примере распределение вероятностей зависит только от переходов с текущего дня на следующий. Это уникальное свойство Марковского процесса – он делает это без использования памяти. Как правило, такой подход не способен создать последовательность, в которой бы наблюдалась какая-либо тенденция. Например, в то время как цепь Маркова способна сымитировать стиль письма, основанный на частоте использования какого-то слова, она не способна создать тексты с глубоким смыслом, так как она может работать только с большими текстами. Именно поэтому цепь Маркова не может производить контент, зависящий от контекста.
Модель
Формально, цепь Маркова – это вероятностный автомат. Распределение вероятностей переходов обычно представляется в виде матрицы. Если цепь Маркова имеет N возможных состояний, то матрица будет иметь вид N x N, в которой запись (I, J) будет являться вероятностью перехода из состояния I в состояние J. Кроме того, такая матрица должна быть стохастической, то есть строки или столбцы в сумме должны давать единицу. В такой матрице каждая строка будет иметь собственное распределение вероятностей.
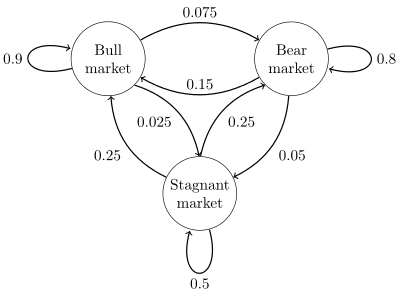
Общий вид цепи Маркова с состояниями в виде окружностей и ребрами в виде переходов.
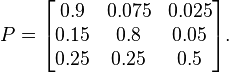
Примерная матрица перехода с тремя возможными состояниями.
Цепь Маркова имеет начальный вектор состояния, представленный в виде матрицы N x 1. Он описывает распределения вероятностей начала в каждом из N возможных состояний. Запись I описывает вероятность начала цепи в состоянии I.
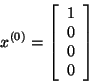
Этих двух структур вполне хватит для представления цепи Маркова.
Мы уже обсудили, как получить вероятность перехода из одного состояния в другое, но что насчет получения этой вероятности за несколько шагов? Для этого нам необходимо определить вероятность перехода из состояния I в состояние J за M шагов. На самом деле это очень просто. Матрицу перехода P можно определить вычислением (I, J) с помощью возведения P в степень M. Для малых значений M это можно делать вручную, с помощью повторного умножения. Но для больших значений M, если вы знакомы с линейной алгеброй, более эффективным способом возведения матрицы в степень будет сначала диагонализировать эту матрицу.
Цепь Маркова: заключение
Теперь, зная, что из себя представляет цепь Маркова, вы можете легко реализовать её на одном из языков программирования. Простые цепи Маркова являются фундаментом для изучения более сложных методов моделирования.



Комментарии