🐍🧩 Обработка вложенных списков и матриц в Python: 5 задач с решениями для совершенствования навыков

Картина

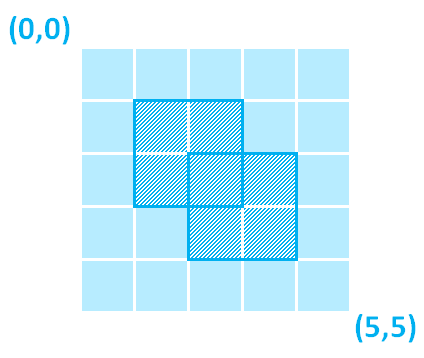
После окончания работы над очередным шедевром кубизма художник решил определить, какая площадь холста осталась незакрашенной. Холст имеет прямоугольную форму; изображение состоит из n прямоугольников, расположенных в целочисленных координатах, параллельно сторонам холста. Напишите программу, которая принимает ширину и высоту холста, а также количество нарисованных на холсте прямоугольников n, и определяет незакрашенную площадь холста.

Формат ввода

В первой строке подаются высота и ширина холста – натуральные числа w и h (1 ≤ w, h ≤ 100); во второй – целое число n, количество прямоугольников (0 ≤ n ≤ 5000). Затем программа получает n строк с координатами левого верхнего и правого нижнего углов прямоугольников – x1, y1, x2, y2.

Формат вывода

Целое число – площадь незакрашенной поверхности холста.

Примеры ввода и вывода

Ввод #1:

        5 5
2
1 1 3 3
2 2 4 4

    

Вывод #1:

        18
    

Ввод #2:

        6 7
3
0 0 5 5
1 1 4 4
2 2 3 3

    

Вывод #2:

        17
    

Решение

Это олимпиадная задача: чтобы решение было засчитано как правильное, код должен удовлетворять жестким требованиям – выполняться не более чем за 1 секунду, и использовать не более 16 Мб памяти. По этой причине эффективно решить эту задачу на Питоне очень сложно: решение «в лоб» на массиве максимального размера исполняется за 1,8-2 секунды, а решение с использованием множеств превышает лимит памяти.

Поскольку поэлементное обновление большого массива в Python происходит слишком медленно, эффективное решение заключается в обновлении массива «кусками»:

        w, h = map(int, input().split())
arr = [[0 for w in range(w)] for h in range(h)]
n = int(input())
for i in range(n):
	x1, y1, x2, y2 = map(int, input().split())
	for x in range(x1, x2):
    	arr[x][y1:y2] = [1] * (y2 - y1)
print(w * h - sum(map(sum, arr)))
    

На массиве максимального размера (при n = 5000) этот код выполняется за 0,703 секунды.

Заполнение матрицы по диагоналям

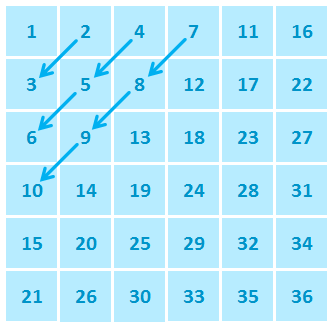
Напишите программу, которая принимает два натуральных числа n и m, создает матрицу размером n × m, и заполняет ее по диагоналям, направленным справа-сверху влево-вниз.

Формат ввода

Строка с числами n и m, разделенными пробелом.

Формат вывода

Матрица, заполненная в соответствии с условием задачи.

Пример ввода и вывода

Ввод #1:

        12 12
    

Вывод #1:

        1   2   4   7   11  16  22  29  37  46  56  67 
3   5   8   12  17  23  30  38  47  57  68  79 
6   9   13  18  24  31  39  48  58  69  80  90 
10  14  19  25  32  40  49  59  70  81  91  100
15  20  26  33  41  50  60  71  82  92  101 109
21  27  34  42  51  61  72  83  93  102 110 117
28  35  43  52  62  73  84  94  103 111 118 124
36  44  53  63  74  85  95  104 112 119 125 130
45  54  64  75  86  96  105 113 120 126 131 135
55  65  76  87  97  106 114 121 127 132 136 139
66  77  88  98  107 115 122 128 133 137 140 142
78  89  99  108 116 123 129 134 138 141 143 144

    

Решение

Способ 1:

        n, m = map(int, input().split())
mt = [[''] * m for i in '1'* n]
d = 1
for k in range(1, n + m + 1):
	for i in range(n):
    	for j in range(m):
        	if i + j + 1 == k:
            	mt[i][j] = str(d).ljust(3)
            	d += 1
[print(*r, sep='') for r in mt]

    

Способ 2:

        n, m = map(int, input().split())
matrix = [[0] * m for _ in range(n)]
template = sorted([(i + j, i, j) for i in range(n) for j in range(m)])
for id, item in enumerate(template):
	matrix[item[1]][item[2]] = id + 1
[print(*[str(item).ljust(3) for item in row]) for row in matrix]
    

Способ 3:

        [n, m] = [int(i) for i in input().split()]
matrix = [['0']*m for _ in range(n)]
num = 0
for d in range(m + n - 1):
	for i in range(n):
    	j = d - i
    	if 0 <= i < n and 0 <= j < m:
        	num += 1
        	matrix[i][j] = str(num).ljust(3)
for i in range(n):
	print(*matrix[i])

    

Максимальный элемент в области

Напишите программу, которая выводит максимальный элемент в заштрихованной области квадратной матрицы.

Формат ввода

В первой строке подается число n – количество строк. Затем программа получает n строк с элементами матрицы.

Формат вывода

Максимальный элемент из заштрихованной области матрицы.

Пример ввода и вывода

Ввод:

        3
1 4 5
6 7 8
1 1 6
    

Вывод:

        8
    

Решение

Способ 1:

        n = int(input())
m = [list(map(int, input().split())) for _ in range(n)]
print(max(max(m[i][j], m[i][~j], m[~i][j], m[~i][~j]) for i in range(n // 2 + 1) for j in range(i + 1)))

    

Способ 2:

        n = int(input())
a = [[*map(int, input().split())] for _ in range(n)]
print(max(a[i][j] for i in range(n) for j in range(n) if j <= i <= n - j - 1 or j >= i >= n - j - 1))

    

Способ 3:

        lst = []
m = int(input())
for i in range(m):
	row = [int(i) for i in input().split()]
	lst.extend(row[:min(i + 1, m - i)])
	lst.extend(row[max(-i - 1, i - m):])
print(max(lst))

    

Сложение матриц

Напишите программу для вычисления суммы двух матриц.

Формат ввода

Программа получает два натуральных числа n и m — количество строк и столбцов в матрицах, далее подаются элементы первой матрицы, после которых следует пустая строка, а затем – элементы второй матрицы.

Формат вывода

Программа должна вывести результирующую матрицу, разделяя элементы символом пробела.

Пример ввода и вывода

Ввод:

        3 3
9 6 3
3 1 1
4 7 5
 
0 3 2
1 7 8
4 2 3
    

Вывод:

        9 9 5
4 8 9
8 9 8
    

Решение

Способ 1:

        n, m = [int(x) for x in input().split()]
A = [[int(x) for x in input().split()] for _ in range(n)]
input()
B = [[int(x) for x in input().split()] for _ in range(n)]
C = [[A[i][j] + B[i][j] for j in range(m)] for i in range(n)]
for x in C:
	print(*x)
    

Способ 2:

        n, m = map(int, input().split())
a = [[*map(int, input().split())] for _ in '.' * n]
input()
b = [[*map(int, input().split())] for _ in '.' * n]
[print(*(i + j for i, j in zip(l, k))) for l, k in zip(a, b)]
    

Способ 3:

        import numpy as np
n, m = map(int, input().split())
a = np.array(list(input().split() for _ in range(n)), int)
p = input()
b = np.array(list(input().split() for _ in range(n)), int)
c = a + b
for i in c:
	print(*i)
    

Строка из треугольника Паскаля

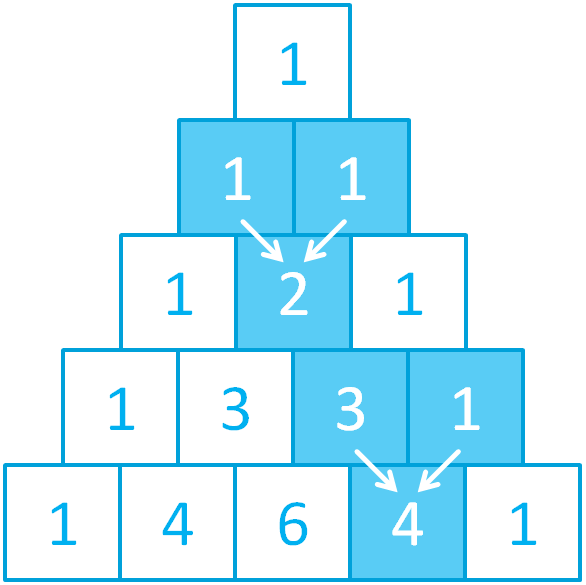
Напишите программу, которая получает на вход число n, и возвращает n-ую строку из треугольника Паскаля в виде списка. Нумерация строк начинается с 0.

Пример ввода и вывода

Ввод:

        3
    

Вывод:

        [1, 3, 3, 1]
    

Решение

Способ 1:

        def trianglePascal(n):
	if n == 0:
    	return [1]
	else:
    	st = trianglePascal(n - 1)
    	return [1] + [st[i] + st[i+1] for i in range(n - 1)] + [1]
n = int(input())
print(trianglePascal(n))

    

Способ 2:

        n = int(input())
li = [1]
for i in range(n):
	for j in range(len(li) - 1):
    	li[j] = li[j] + li[j + 1]
	li.insert(0, 1)
print(li)
    

Способ 3:

        from math import factorial
n = int(input())
print([int(factorial(n) / (factorial(j) * factorial(n - j))) for j in range(n + 1)])
    

Способ 4:

        l = [1]
for _ in range(int(input())):
	l = [a + b for a, b in zip([*l, 0], [0, *l])]
print(l)

    

Способ 5:

        import math
def fac(num):
	return math.factorial(num)
def pasc(n):
	row = [1]
	for i in range(1, n + 1):
    	row.append(int(fac(n) / (fac(i) * fac(n - i))))
	return row
n = int(input())
print(pasc(n))

    

Материалы по теме

• 🐍 Словари в Python: 12 задач для начинающих с решениями
• 🐍 5 задач с решениями на Python для начинающих разработчиков
  
• 🐍 5 классических задач по Python для начинающих с решениями