📊 Обучение Data Science: 11 необходимых специалисту по анализу данных концепций из статистики

Статистика – это использование математики (прежде всего теории вероятностей) для выполнения технического анализа данных. Понимание основных ее концепций поможет Data Scientist формировать конкретные выводы, а не просто строить догадки.

Во вступительных публикациях серии мы писали о том, какие знания по математике нужны специалисту по анализу данных. Углубляя тему, расскажем об 11 важнейших концепциях из статистики, без которых не может обойтись ни один Data Scientist.

Случайная величина

Случайная величина – это переменная, значения которой определяются случайным экспериментом. Случайные величины используются в качестве модели для процессов генерации данных, которые мы хотим исследовать.

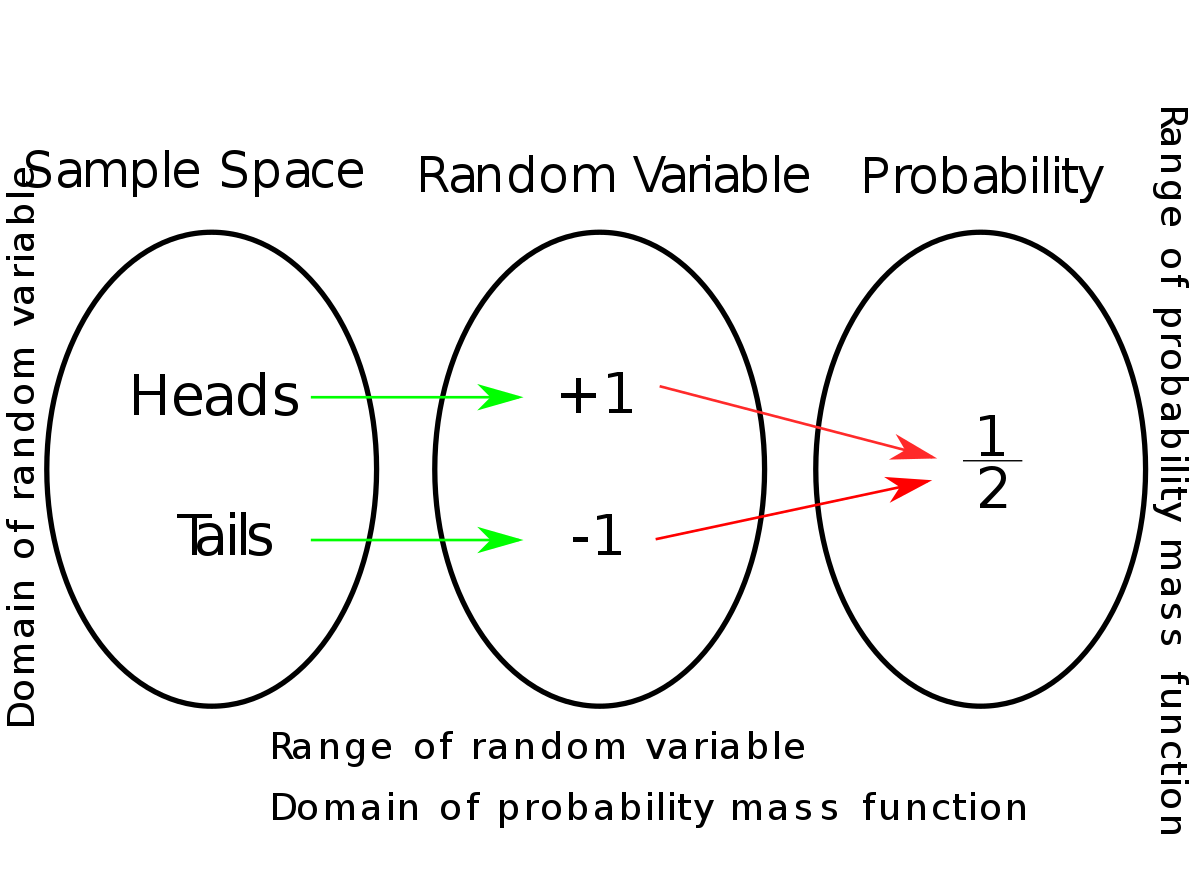
Свойства данных тесно связаны с соответствующими свойствами случайных величин, вроде ожидаемого значения, дисперсии и корреляции. Зависимости между случайными величинами являются решающим фактором, позволяющим прогнозировать неизвестные значения на основе известных – на этом основано контролируемое машинное обучение.

P-value

P-value – это мера вероятности значения, которое принимает случайная величина. Предположим, что у нас есть случайная величина A и значение x. P-value значения x – вероятность того, что A принимает это или любое другое значение, которое имеет тот же или меньший шанс быть наблюдаемым. На практике если значение Р меньше альфа (скажем, 0,05), мы говорим, что вероятность того, что результат мог произойти случайно, составляет менее 5%.

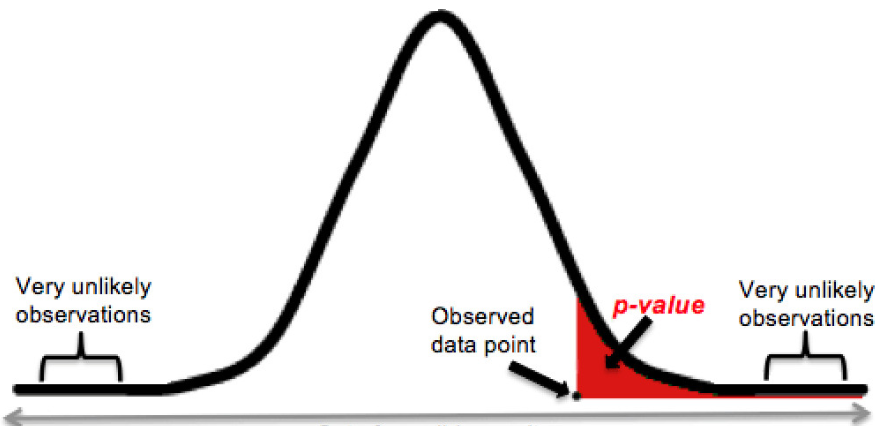
P-value используется при оценке того, насколько несовместимы данные с построенной статистической моделью, но необходимо также учитывать контекстуальные факторы, вроде дизайна исследования, качества измерений, внешних доказательств изучаемого явления и обоснованности предположений, лежащих в основе анализа данных.

Нормальное распределение

Нормальное распределение также известно как распределение Гаусса, которое определяется его средним значением и стандартным отклонением. Среднее смещает распределение пространственно, где стандартное отклонение управляет спредом. Мы знаем среднее значение набора данных и разброс данных с гауссовым распределением.

Распределение Пуассона такое же, как и нормальное, но с добавлением асимметрии. Оно имеет относительно равномерный разброс во всех направлениях, как и нормальный во время малозначимой асимметрии. При высоком значении асимметрии разброс данных будет различным в разных направлениях.

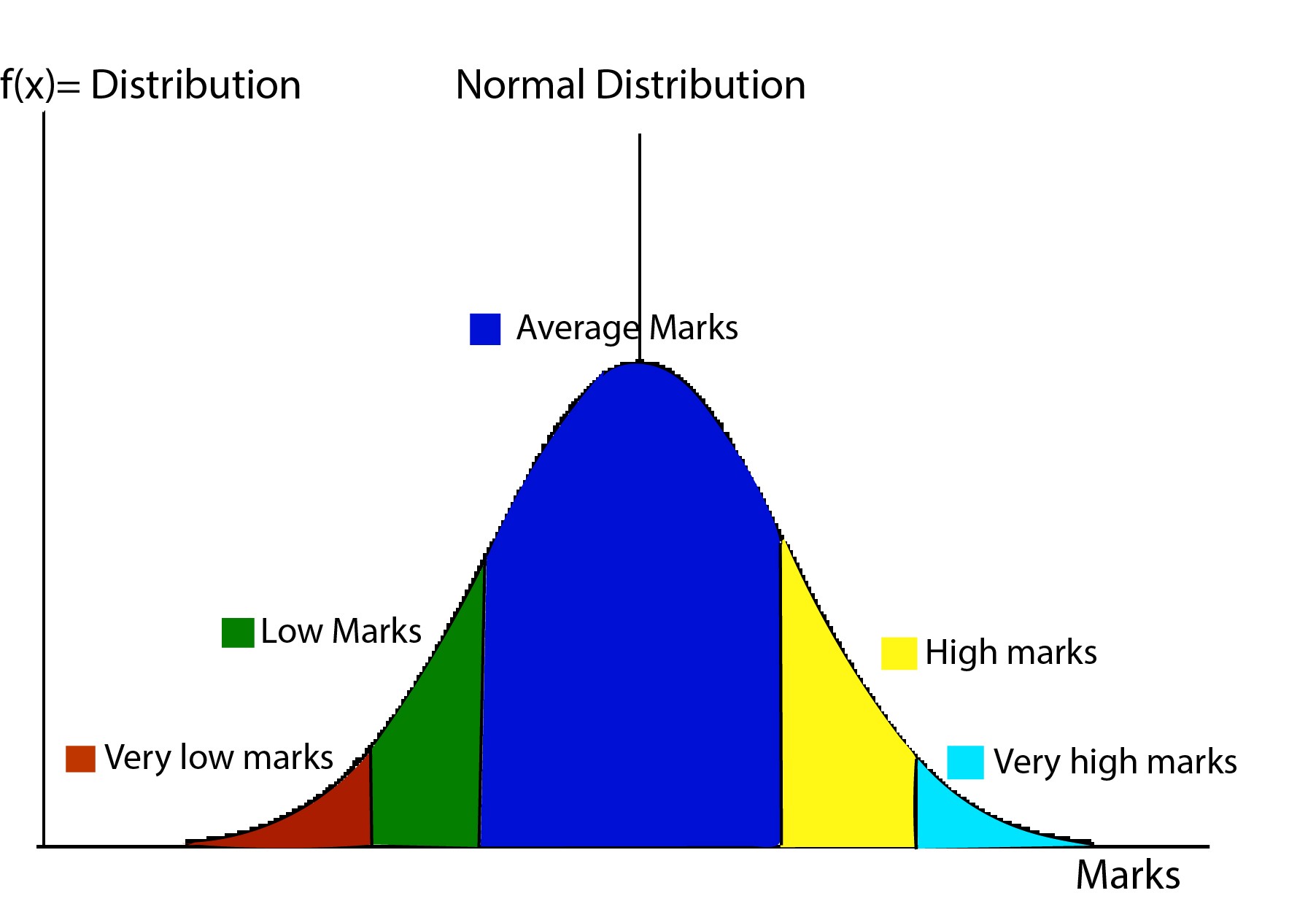
Существует множество распределений, которые помогают интерпретировать категориальные данные с равномерным распределением. Распределения вероятностей помогает вычислить доверительные интервалы для параметров и критические области для проверки гипотез. Для одномерных данных полезно определить подходящую модель распределения данных. Статистические интервалы и проверка гипотез также зависят от предположений о распределении переменных.

Меры центральной тенденции

Центральная тенденция – это центральное (или типичное) значение распределения вероятностей. Наиболее распространенными показателями центральной тенденции являются среднее, медиана и мода.

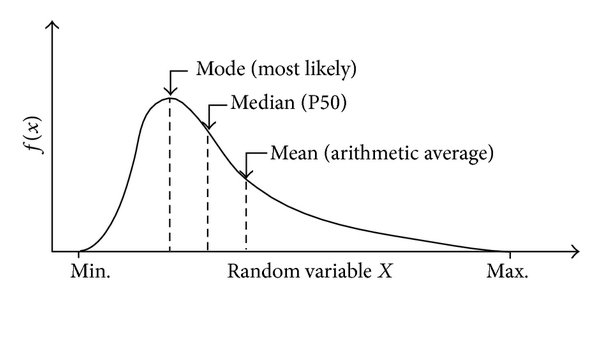
Среднее (mean) – это среднее значение последовательных значений.

Медиана (median) – это значение в середине, когда значения сортируются в порядке возрастания или убывания.

Мода (mode) – это значение, которое появляется чаще всего.

Снижение размерности

Термин уменьшение размерности интуитивно понятен. У нас есть набор данных, и мы хотели бы уменьшить количество измерений. В науке о данных это число переменных признаков.

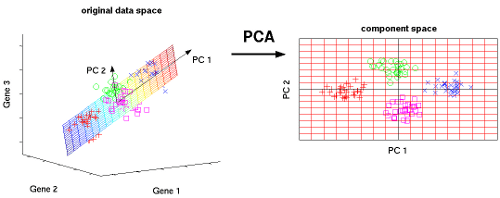
Наиболее распространенным статистическим методом, используемым для уменьшения размерности, является метод главных компонент (с англ. Principal component analysis, PCA), который создает векторные представления объектов, показывающие, насколько они важны для вывода (их корреляцию). Метод главных компонент или PCA можно использовать для выполнения уменьшения размерности данных с наименьшей потерей информации.

Дисперсия и стандартное отклонение

Дисперсия – это мера вариации между значениями. Она рассчитывается путем сложения квадратов разностей каждого значения и среднего значения, а затем деления суммы на количество выборок.

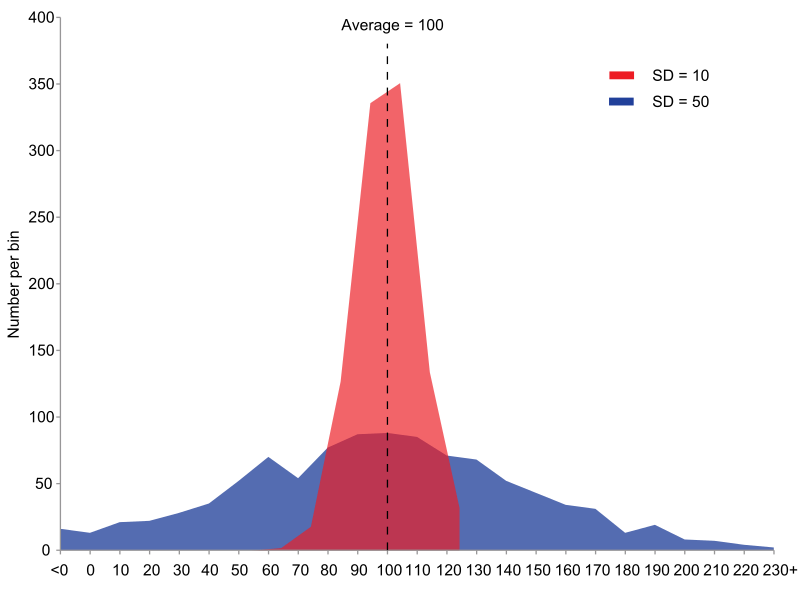
Стандартное отклонение (с англ. standard deviation, SD) – это мера того, насколько разбросаны значения. Если быть более точным, это квадратный корень из дисперсии.

Среднее, медиана, мода, дисперсия и стандартное отклонение – это основные статистические показатели, которые используются для описания переменных на начальном этапе работы с данными.

Ковариации и корреляции

Ковариация – это количественная мера, которая представляет, насколько вариации двух переменных соответствуют друг другу. Чтобы быть более конкретным, ковариация сравнивает две переменные с точки зрения отклонений от их среднего (или ожидаемого) значения. Ковариация переменной с самой собой – это дисперсия переменной.

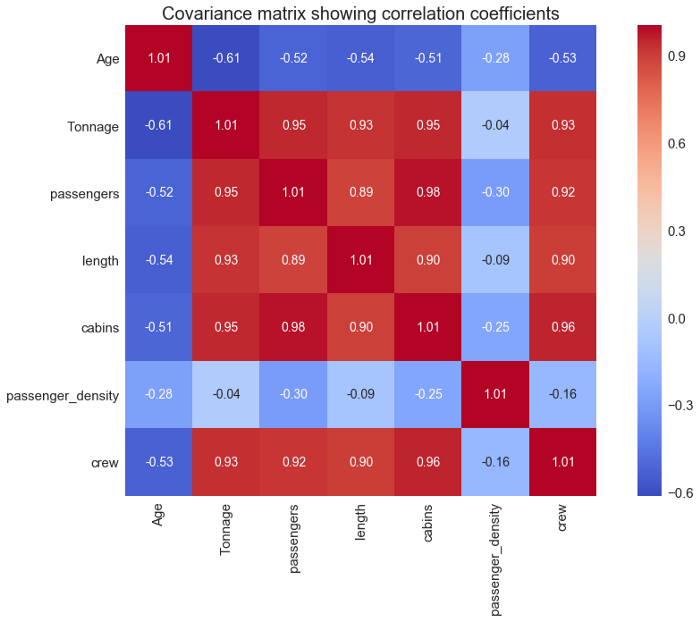
Корреляция – это нормализация ковариации на стандартное отклонение каждой переменной. Эта нормализация отменяет единицы измерения, и значение корреляции всегда находится между 0 и 1. Обратите внимание, что это абсолютное значение. В случае отрицательной корреляции между двумя переменными, корреляция находится между 0 и -1. Если мы сравниваем отношения между тремя или более переменными, лучше использовать корреляцию, потому что диапазоны значений или единицы измерения могут вызвать ложные предположения.

Центральная предельная теорема

Во многих областях, включая естественные и социальные науки, когда распределение случайной величины неизвестно, используется нормальное распределение. Центральная предельная теорема (с англ. Central limit theorem, CLT) обосновывает, почему в таких случаях можно использовать нормальное распределение. Согласно CLT, по мере того как мы берем больше выборок из распределения, средние значения выборок будут стремиться к нормальному распределению независимо от распределения населения.

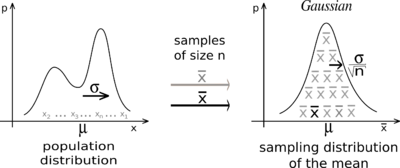
Возьмем выборку из набора данных и вычислим среднее ее значение. После многократного повторения вы нанесете средние значения и их частоты на график и увидите, что была создана колоколообразная кривая, также известная как нормальное распределение. Среднее значение этого распределения будет очень похоже на исходные данные. Вы можете повысить точность среднего значения и уменьшить стандартное отклонение, взяв большие выборки данных и больше выборок в целом.

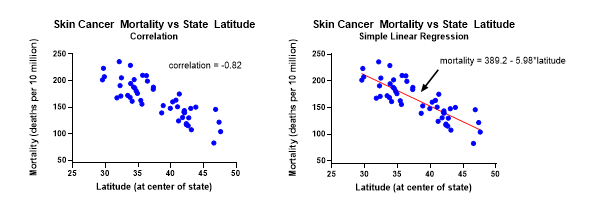
Линейная и логистическая регрессии

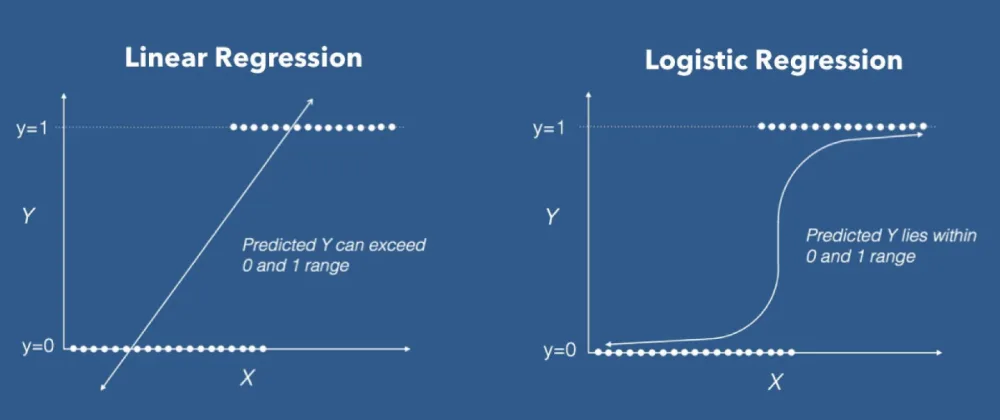
Линейная регрессия является одним из наиболее фундаментальных алгоритмов, используемых для моделирования отношений между зависимой переменной и одной или несколькими независимыми переменными. Данный алгоритм включает в себя поиск линии наилучшего соответствия, представляющей две или более переменных.

Линия наилучшего соответствия находится путем минимизации квадратов расстояний между точками и линией наилучшего соответствия – это известно как минимизация суммы квадратов остатков. Остаток равен прогнозируемому значению минус фактическое значение.

Логистическая регрессия аналогична линейной регрессии, но используется для моделирования вероятности дискретного числа исходов, обычно двух.

Условная вероятность

Условная вероятность – это вероятность того, что событие произойдет, и всегда принимает значение от 0 до 1 включительно. Вероятность события A обозначается как p(A) и вычисляется как число желаемого результата, деленное на число всех исходов. Например, когда вы бросаете кубик, вероятность получить число меньше четырех равна 2/3. Это значит, если нам известно, что это нечетное число, то в двух из трех случаев сумма кубиков будет меньше четырех.

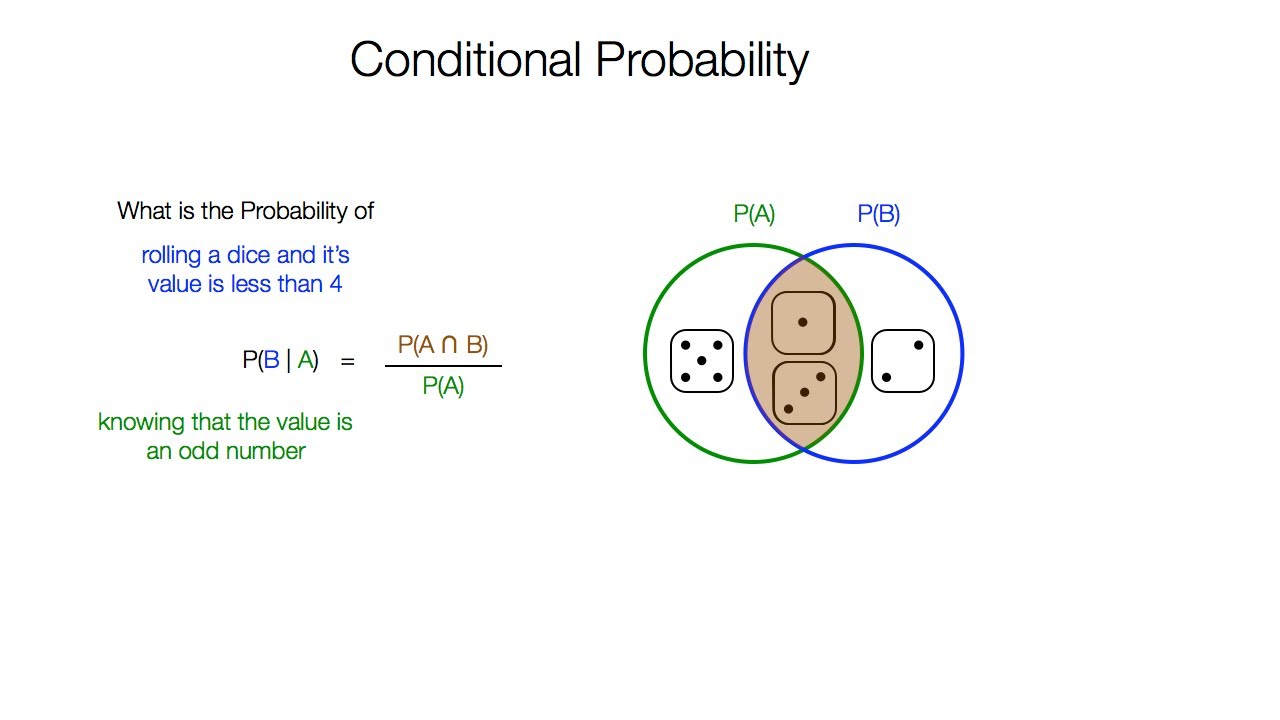
Условная вероятность – это вероятность того, что событие A произойдет при условии, что другое событие, которое уже произошло, имеет отношение к событию A.

Теорема Байеса

Теорема Байеса – это условное вероятностное утверждение. По существу она рассматривает вероятность того, что одно событие (B) произойдет, учитывая, что другое событие (A) уже произошло.

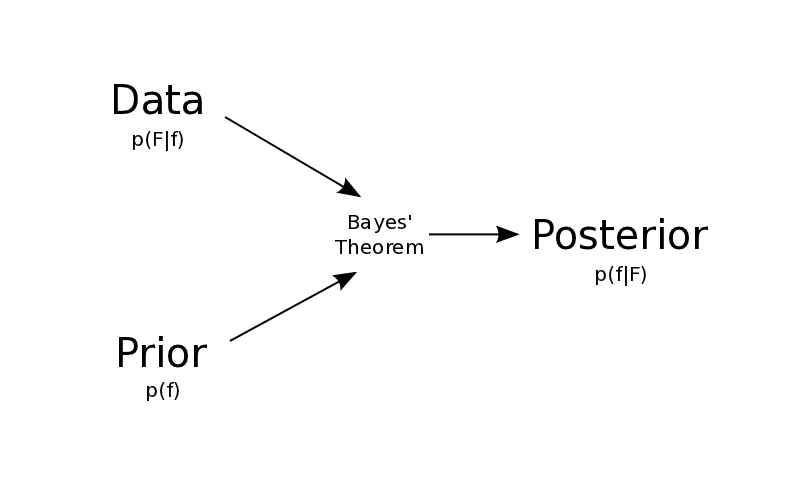
Это один из самых популярных алгоритмов машинного обучения. Наивный байесовский классификатор, построен на этих двух концепциях. Кроме того если вы заинтересованы в области онлайн-машинного обучения, вы, скорее всего, будете использовать байесовские методы.

Подробнее об этих и других концепциях статистики вы сможете узнать из нашей подборки курсов, видеолекций и книг.

Курсы

На русском

• Основы статистики
• Просто о статистике (с использованием R)
• Машинное обучение: от статистики до нейросетей
• Математическая статистика и А/В тестирование

На английском

• Intro to Descriptive Statistics
• Basic Statistics
• Bayesian Statistics: From Concept to Data Analysis
• Probability Theory, Statistics and Exploratory Data Analysis

Видеолекции

Statistics And Probability Tutorial | Statistics And Probability for Data Science by Edureka

Statistics and Probability Full Course || Statistics For Data Science

Statistics – A Full University Course on Data Science Basics

Анализ данных на Python в примерах и задачах

Книги

Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python (второе издание на английском) by Peter C. Bruce, Andrew Bruce, Peter Gedeck

An Introduction to Statistical Learning: With Applications in R by Gareth M. James, Daniela Witten, Trevor Hastie, Robert Tibshirani

Think Stats by Allen B. Downey

Практическая статистика для специалистов Data Science (первое издание на русском языке) от Брюса Эндрю и Брюса Питер

Искусство статистики. Как находить ответы в данных от Дэвида Шпигельхалтер

Используя статистику, мы можем получить глубокое представление о структурировании данных. Это позволяет оптимально применять методы Data Science, чтобы добыть еще больше ценной информации, на которой будут основаны наши решения.