Небольшое руководство по анализу и жанровой классификации аудио/музыкальных сигналов на Python.

Разнообразные сервисы и платформы потоковой музыки, такие как Spotify и SoundCloud, стремятся постоянно улучшать способы подбора и рекомендации композиций для своих пользователей. Системы жанровой классификации музыки совершенствуются, а в их основе лежит машинное обучение.
В ход идут все известные методы: от NLP и коллаборативной фильтрации до deep learning. Песни распределяются по жанрам на основе их темпа, акустики, энергичности, танцевальности и десятков других характеристик.
В этой статье мы разбираемся, как анализировать и классифицировать музыкальные сигналы с помощью средств, которые предоставляет язык Python.
Если вы начинающий программист, обратите внимание на эти лучшие для изучения Python бесплатные книги, которые мы собрали специально для вас.
Обработка звука на Python
Звук – это сигнал с набором определенных параметров: частота, полоса пропускания пропускная способность, децибелы и прочее. Типичный звуковой сигнал может быть выражен как функция от амплитуды и времени:
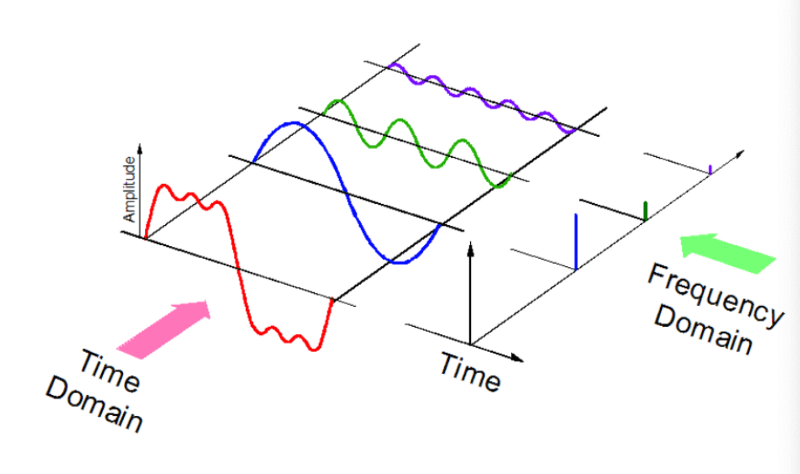
Компьютеры могут работать с различными аудиоформатами:
- mp3;
- wma (Windows Media Audio);
- wav (Waveform Audio File).
Python библиотеки для работы со звуком
Для работы со звуком на Python существует ряд мощных библиотек, например, Librosa или PyAudio, а также встроенные модули, поддерживающие базовую функциональность.
Мы будем использовать две библиотеки:
Librosa
Librosa может работать с любыми звуковыми сигналами, но ориентирована в основном именно на музыку. Она позволяет создать полноценную систему извлечения музыкальной информации (MIR). Модуль прекрасно документирован, кроме того, существует множество руководств по использованию. Принципы разработки подробно разобраны в этой статье с конференции SciPy2015.
Установка Python библиотеки librosa выглядит так:
pip install librosa
Или так:
conda install -c conda-forge librosa
Вы также можете установить модуль ffmpeg со множеством готовых решений для конвертации аудиосигналов.
IPython.display.Audio
IPython.display.Audio позволяет воспроизводить аудио непосредственно в Jupyter Notebook.
Загрузка аудиофайла
import librosa audio_path = '../T08-violin.wav' x , sr = librosa.load(audio_path) print(type(x), type(sr)) <class 'numpy.ndarray'> <class 'int'> print(x.shape, sr) (396688,) 22050
Скачать аудиофайл T08-violin.wav можно здесь.
Этот код превращает временной ряд аудио в NumPy массив с частотой дискретизации (sr) 22 кГц. Дефолтное значение можно изменить, например, на 44.1 кГц:
librosa.load(audio_path, sr=44100)
или совсем отключить семплирование:
librosa.load(audio_path, sr=None)
Частота дискретизации – это количество семплов (колебаний) звука, передаваемого в секунду, измеренное в Гц или кГц.
Воспроизведение
Для воспроизведения аудио используем IPython.display.Audio:
import IPython.display as ipd ipd.Audio(audio_path)
Этот код в Jupyter Notebook возвращает вот такой виджет:

Та же самая композиция в SoundCloud:
[embed]https://soundcloud.com/parul-pandey-323138580/t08-violin[/embed]
Визуализация звука
Форма волны
Используя librosa.display.waveplot, можно визуализировать массив аудиоданных:
%matplotlib inline import matplotlib.pyplot as plt import librosa.display plt.figure(figsize=(14, 5)) librosa.display.waveplot(x, sr=sr)
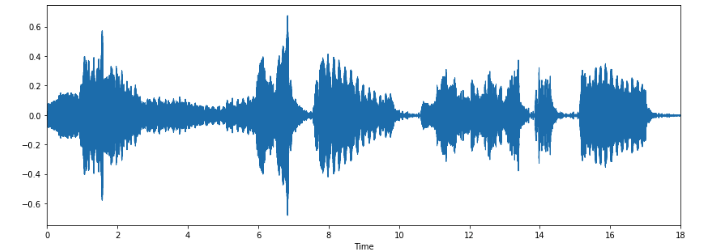
Мы получили график амплитудной огибающей сигнала.
Спектрограмма
Спектрограмма – это визуальное представление спектра частот звуковых или других сигналов, изменяющихся со временем. Иногда их также называют сонограммами. На двумерных графиках по первой оси задается частота, по второй – время.
Для создания спектрограммы на Python используем librosa.display.specshow.
X = librosa.stft(x) Xdb = librosa.amplitude_to_db(abs(X)) plt.figure(figsize=(14, 5)) librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz') plt.colorbar()
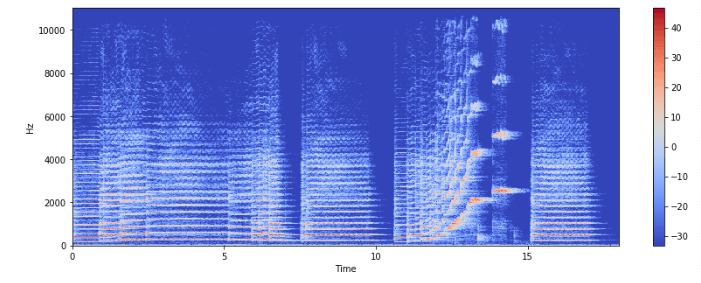
Вертикальная ось – это частоты (от 0 до 10 кГц), а горизонтальная – время клипа. Поскольку все значимые изменения происходят в нижней части спектра, частотную ось можно преобразовать в логарифмическую.
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log') plt.colorbar()
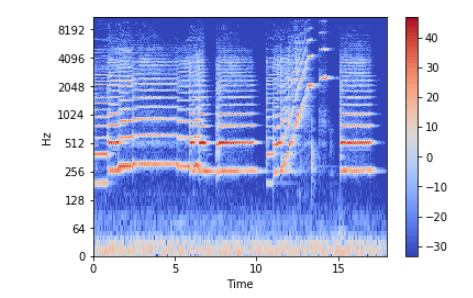
Запись аудио
librosa.output.write_wav сохраняет NumPy массив в WAV-файл:
librosa.output.write_wav('example.wav', x, sr)
Создание звукового сигнала
Давайте теперь создадим на Python звуковой сигнал с частотой 220 Гц. Это NumPy массив, который будет передан в функцию Audio:
import numpy as np
sr = 22050 # sample rate
T = 5.0 # seconds
t = np.linspace(0, T, int(T*sr), endpoint=False) # time variable
x = 0.5*np.sin(2*np.pi*220*t)# pure sine wave at 220 Hz
# Воспроизведение
ipd.Audio(x, rate=sr) # load a NumPy array
# Сохранение
librosa.output.write_wav('tone_220.wav', x, sr)
[embed]https://soundcloud.com/parul-pandey-323138580[/embed]
Ура, вы создали первую композицию!
Извлечение сущностей
Каждый звуковой сигнал имеет множество характеристик, из которых следует отобрать нужные. Процесс извлечения информации для анализа называется извлечением объектов или извлечением сущностей (feature extraction).
Освоиться в мире машинного обучения помогут наши полезные руководства и книги по Python:
- Настраиваем Python для машинного обучения на Windows
- FeatureSelector: отбор признаков для машинного обучения на Python
- NLP – это весело! Обработка естественного языка на Python
- 11 книг по ИИ и Data Science для изучения в 2019
Частота перехода через нуль
Частота пересечения нуля (zero crossing rate) – это частота изменения знака сигнала, т. е. частота, с которой сигнал меняется с положительного на отрицательный и обратно. Эта функция широко используется как для распознавания речи, так и для извлечения музыкальной информации. Для металла и рока этот параметр обычно выше, чем для других жанров, из-за большого количества ударных.
Рассчитаем частоту перехода через нуль для нашего примера на Python:
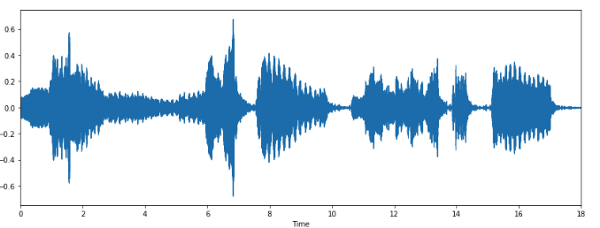
x, sr = librosa.load('../T08-violin.wav')
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr)
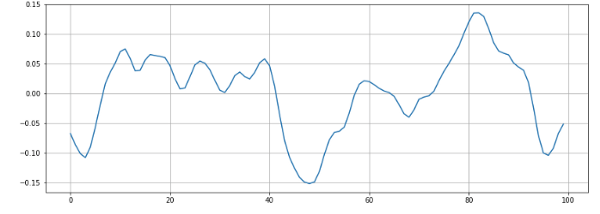
n0 = 9000 n1 = 9100 plt.figure(figsize=(14, 5)) plt.plot(x[n0:n1]) plt.grid()
На графике мы видим 6 пересечений нуля. Давайте проверим:
zero_crossings = librosa.zero_crossings(x[n0:n1], pad=False) print(sum(zero_crossings)) # 6
Все правильно.
Спектральный центроид
Спектральный центроид указывает, где расположен "центр масс" звука, и рассчитывается как средневзвешенное значение всех частот.
В блюзовых композициях частоты равномерно распределены, и центроид лежит где-то в середине спектра. В металле наблюдается выраженное смещение частот к концу композиции, поэтому и спектроид лежит ближе к концу спектра.
Вычислим спектральный центроид для каждого фрейма с помощью librosa.feature.spectral_centroid:
spectral_centroids = librosa.feature.spectral_centroid(x, sr=sr)[0] spectral_centroids.shape (775,) # Вычисление времени для визуализации frames = range(len(spectral_centroids)) t = librosa.frames_to_time(frames) # Нормализация спектрального центроида def normalize(x, axis=0): return sklearn.preprocessing.minmax_scale(x, axis=axis) # Построение графика librosa.display.waveplot(x, sr=sr, alpha=0.4) plt.plot(t, normalize(spectral_centroids), color='r')
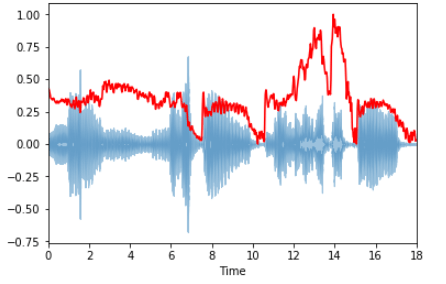
На графике ярко выражен рост частот к концу спектра.
Спектральный спад частоты
Это мера формы сигнала, представляющая собой частоту, ниже которой лежит определенный процент от общей спектральной энергии, к примеру, 85%.
librosa.feature.spectral_rolloff вычисляет спад частоты для каждого фрейма:
spectral_rolloff = librosa.feature.spectral_rolloff(x+0.01, sr=sr)[0] librosa.display.waveplot(x, sr=sr, alpha=0.4) plt.plot(t, normalize(spectral_rolloff), color='r')
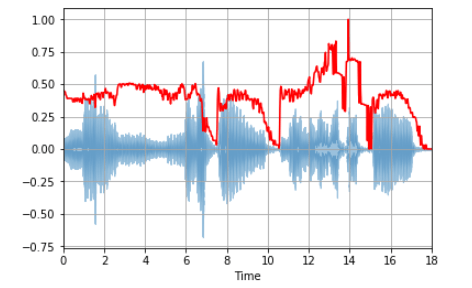
Мел-частотные кепстральные коэффициенты
Мел-частотные кепстральные коэффициенты (MFCC) сигнала – небольшой набор характеристик (обычно около 10-20) которые сжато описывают общую форму спектральной огибающей. Этот параметр моделирует характеристики человеческого голоса.
Для примера возьмем простую циклическую волну:
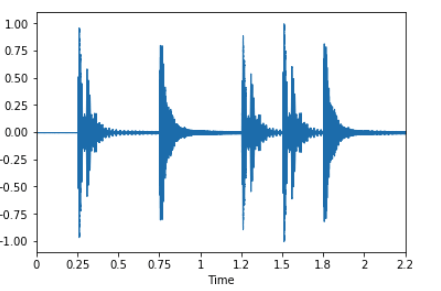
x, fs = librosa.load('../simple_loop.wav')
librosa.display.waveplot(x, sr=sr)
И вычислим с помощью librosa.feature.mfcc эти коэффициенты:
mfccs = librosa.feature.mfcc(x, sr=fs) print mfccs.shape (20, 97) # Отображение librosa.display.specshow(mfccs, sr=sr, x_axis='time')
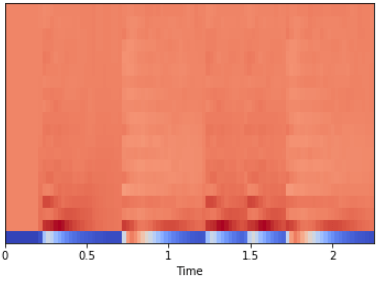
Мы также можем выполнить масштабирование таким образом, чтобы каждое измерение коэффициента имело нулевое среднее и единичную дисперсию:
import sklearn mfccs = sklearn.preprocessing.scale(mfccs, axis=1) print(mfccs.mean(axis=1)) print(mfccs.var(axis=1)) librosa.display.specshow(mfccs, sr=sr, x_axis='time')
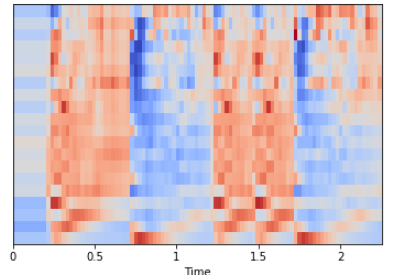
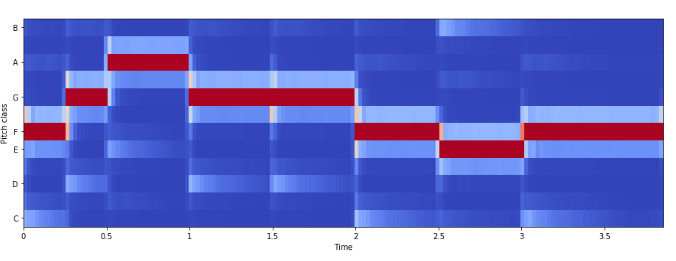
Частота цветности
Цветность (chroma features) – это интересное и мощное представление для музыкального звука, при котором весь спектр проецируется на 12 контейнеров, представляющих 12 различных полутонов музыкальной октавы.
Для вычислений используем librosa.feature.chroma_stft:
# Загрузка файла
x, sr = librosa.load('../simple_piano.wav')
hop_length = 512
chromagram = librosa.feature.chroma_stft(x, sr=sr, hop_length=hop_length)
plt.figure(figsize=(15, 5))
librosa.display.specshow(chromagram, x_axis='time', y_axis='chroma', hop_length=hop_length, cmap='coolwarm')
Пример: классификация песен по жанрам
Теперь вы знакомы со структурой акустического сигнала и особенностями процесса извлечения музыкальной информации. Пришла пора использовать полученные знания на практике, используя Python библиотеки для работы со звуком.
Цель
Попробуем смоделировать жанровый классификатор музыки. Он вам очень пригодится, если понадобится разобрать кучу неизвестных mp3-файлов.
Набор данных
Возьмем знаменитый набор данных GITZAN. Он использовался для известного исследования Musical genre classification of audio signals (G. Tzanetakis, P. Cook).
Набор состоит из 1000 звуковых дорожек длиной 30 секунд и содержит 10 жанров: блюз, классика, кантри, диско, хип-хоп, джаз, регги, рок, метал и поп. В каждом жанре 100 звуковых клипов.
Предварительная обработка
Перед обучением модели классификации нужно преобразовать необработанные данные из звуковых выборок в более осмысленное представление. Преобразуем клипы в формат wav, чтобы Python мог с ними мог работать, с помощью модуля SoX.
sox input.au output.wav
Вы можете воспользоваться удобной шпаргалкой по SoX.
Классификация
Извлечение сущностей
Теперь извлечем из аудиофайлов всю необходимую информацию:
- мел-частотные кепстральные коэффициенты,
- спектральный центроид,
- частоту перехода через нуль,
- частоты цветности,
- спектральный спад частоты.
Все эти функции сохраним в .csv-файле.
Классификация
Теперь можно использовать существующие алгоритмы классификации для распределения песен по жанрам.
Вы можете либо использовать непосредственно спектрограммы, либо извлечь сущности и применять модели классификации на них. Здесь перед вами открывается огромный простор для экспериментов.
Здесь вы можете изучить пример использования сверточной нейронной сети (CNN) на спектрограммах.
Что дальше
Жанровая классификация – лишь одна из многих прикладных отраслей извлечения музыкальной информации.
Мы разобрались, как организовывается на Python работа с музыкальными сигналами. Эти знания можно применить для решения множества задач: отслеживания ритма, создания музыки, рекомендательных систем, распознавания инструментов и т. д.
Анализ музыкальной информации – это очень широкая и интересная сфера деятельности.
Оригинал: Music Genre Classification with Python


Комментарии