Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Предположим, есть задача, данные в которой не меняются между запросами. Стоит лишь подвергнуть эти данные предварительной обработке, а уже затем с большой эффективностью (O(1)) получать ответы на запросы.
Запрос о сумме
Обозначим sum(a, b) как сумму элементов массива в диапазоне [a..b]. Любой запрос о сумме можно эффективно обработать, если обработать входной массив и построить по нему массив префиксных сумм. Эта структура данных донельзя проста: каждый элемент массива равен сумме нескольких первых элементов исходного массива, т.е. значение k-го элемента равно sum(0, k). Обозначим массив как pref[n] и применим динамическое программирование: pref[i + 1] = pref[i] + a[i].
После построения массива pref любое значение sum(a, b) можно вычислить по формулеsum(a, b) = pref[b] – pref[a]. Поскольку при заполнении мы, фактически, используем 1-индексацию, a рассматривается включительно, b – нет. Поэтому важно не забыть уменьшить a на единицу.
Ещё один важный момент: поскольку в C++ отсутствует длинная арифметика, необходимо использовать кольцо вычетов по модулю (как правило, 109 + 7). Код выглядит следующим образом:
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
using namespace std;
const int SIZE = 100100;
const int MOD = 1000000007;
int64_t pref[SIZE];
int a[SIZE];
int main()
{
int n;
cin >> n;
forn (i, n) cin >> a[i];
forn (i, n) pref[i + 1] = (pref[i] + a[i]) % MOD;
int q;
cin >> q;
forn (r, q)
{
int a, b;
cin >> a >> b;
cout << (pref[b] - pref[a - 1] + MOD) % MOD << "\n";
}
return 0;
}
Многомерный случай
Идея массива префиксных сумм обобщается и на многомерный случай. Предположим, мы имеем следующий массив:

Тогда сумму по оранжевому подмассиву можно посчитать как S(o+r+b+g) – S(r + b) – S(r + g) + S(r), где o, r, b, g – названия цветов orange, red, blue, green соответственно.
Код (в этот раз используем 0-индексацию):
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
using namespace std;
const int SIZE = 1010;
const int MOD = 1000000007;
int64_t pref[SIZE][SIZE];
int a[SIZE][SIZE];
int main()
{
int n, m;
cin >> n >> m;
pref[0][0] = a[0][0];
for (int i = 1; i < n; ++i) pref[i][0] = (pref[i - 1][0] + a[i][0]) % MOD;
for (int j = 1; j < m; ++j) pref[0][j] = (pref[0][j - 1] + a[0][j]) % MOD;
for (int i = 1; i < n; ++i)
{
for (int j = 1; j < m; ++j)
{
pref[i][j] = (((pref[i - 1][j] + pref[i][j - 1]) % MOD - pref[i - 1][j - 1] + MOD) % MOD + a[i][j]) % MOD;
}
}
return 0;
}
Запрос о минимуме
Обозначим как min(a, b) минимальный элемент массива в диапазоне [a..b]. Рассмотрим способ, позволяющий находить минимум за O(1) и O(n*logn). Этот метод называется алгоритмом разреженной таблицы или sparse table.
Идея заключается в том, чтобы заранее вычислить min(a, b) для случаев, когда b – a + 1 (т.е. длина диапазона) является степенью двойки.
Количество предвычисляемых значений имеет порядок O(n*logn), поскольку существует O(logn) длин диапазонов, являющихся степенью двойки. Эти значения можно эффективно вычислять по рекуррентной формуле
min(a, b) = min(min(a, a + w — 1), min(a + w, b))
Согласно этой формуле b – a + 1 – степень двойки, а w = (b — a + 1) / 2;
Вычисление всех значений занимает время O(n*logn).
После этого любое значение min(a, b) можно вычислить за O(1), взяв минимум два предвычисленных значения. Пусть k – небольшая степень двойки, не превосходящая b — a + 1. Значение min(a, b) вычисляется по формуле
min(a, b) = min(min(a, a + k — 1), min(b — k + 1, b))
В этой формуле диапазон [a..b] представлен как объединение двух диапазонов длины k: [a .. a + k – 1] и [b – k + 1 .. b].
Иными словами, выбирается такое k, которое является степенью двойки, но не превосходит по длине данный отрезок; диапазон разбивается на два различных по описанным формулам, в каждом из них ищется минимум, далее сравнивается. Алгоритм для максимума аналогичен алгоритму для минимума. Реализация для максимума:
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
using namespace std;
const int SIZE = 1000100;
int64_t stable[SIZE][20]; // максимум рассмотрим 20 степеней двойки
int main()
{
int n;
cin >> n;
vector<int> a(n);
vector<int> max_k(n + 1);
forn (i, n) cin >> a[i];
forn (i, n) stable[i][0] = a[i]; // заполняем для нулевой степени
for (int i = 1; i <= n; ++i)
{
int k;
for (k = 0; (1 << k) <= i; ++k)
{
max_k[i] = k - 1; // перебираем все позиции [1..n] и выбираем степень двойки для каждой из них
}
}
for (int k = 1; k < 20; ++k)
{
for (int i = 0; i + (1 << k) - 1 < n; ++i)
{
stable[i][k] = max(stable[i][k - 1], stable[i + (1 << (k - 1))][k - 1]); // заполняем таблицу
}
}
int q;
cin >> q;
forn (r, q)
{
int a, b;
cin >> a >> b;
--a;
int len = b - a;
int k = max_k[len];
cout << max(stable[a][k], stable[b - (1 << k)][k]) << "\n";
}
return 0;
}
Дерево Фенвика
Довольно простая и быстрая, но совсем не очевидная в плане идеи и понимания структура данных. Позволяет находить сумму на префиксе и изменять отдельные элементы за O(logn).
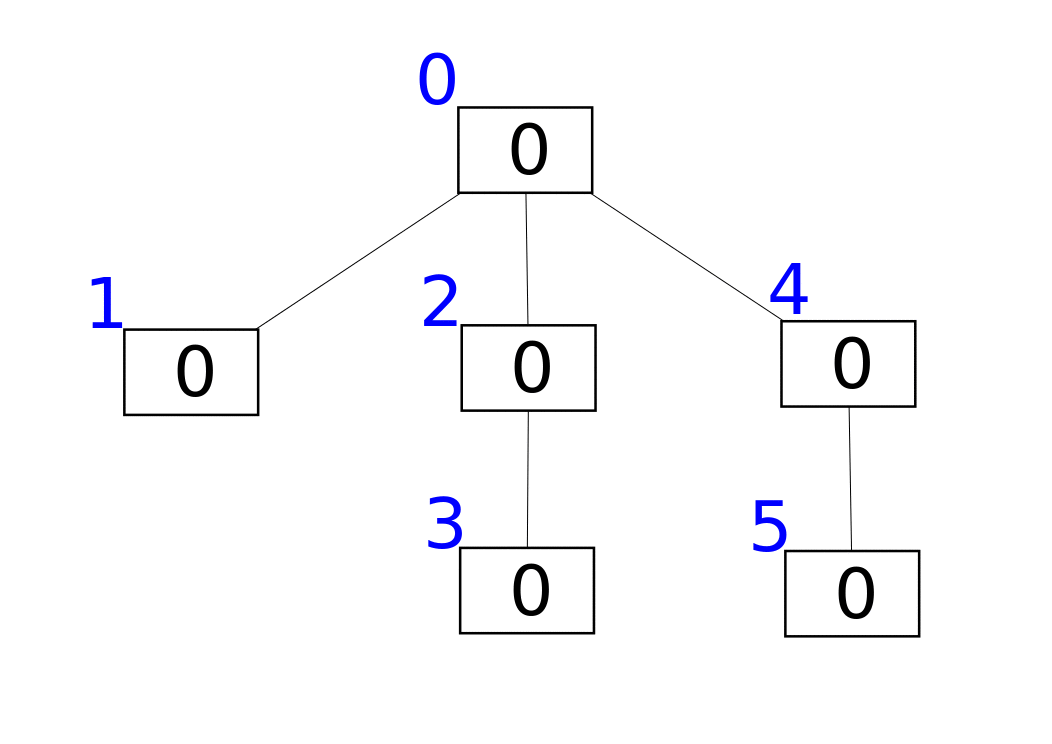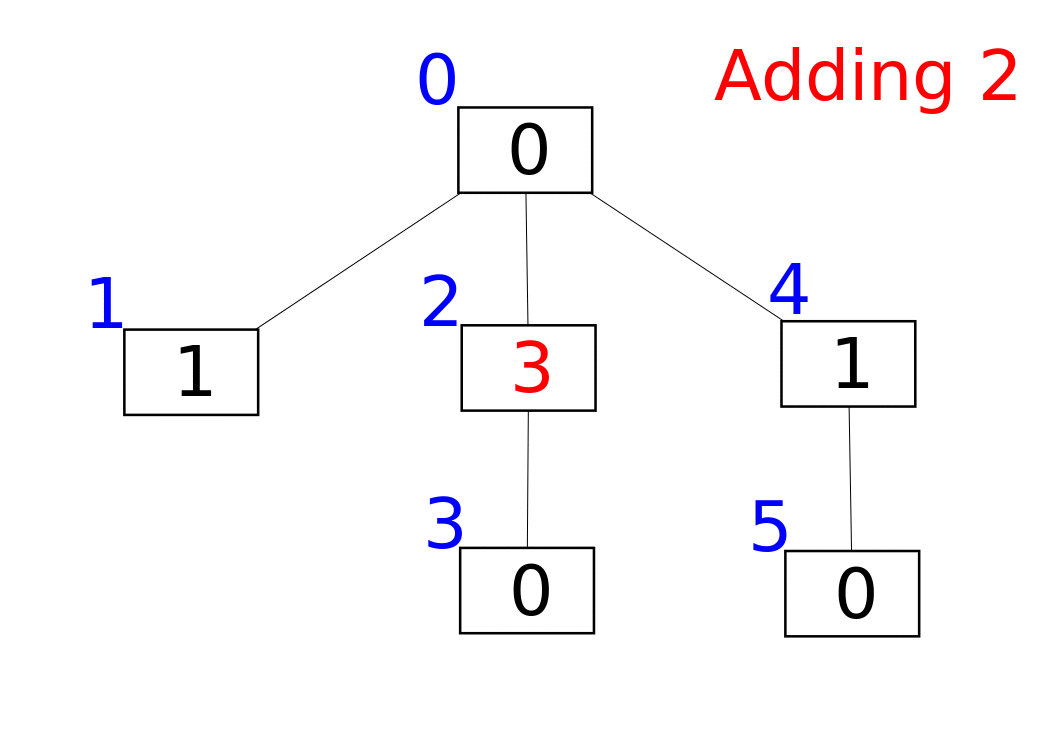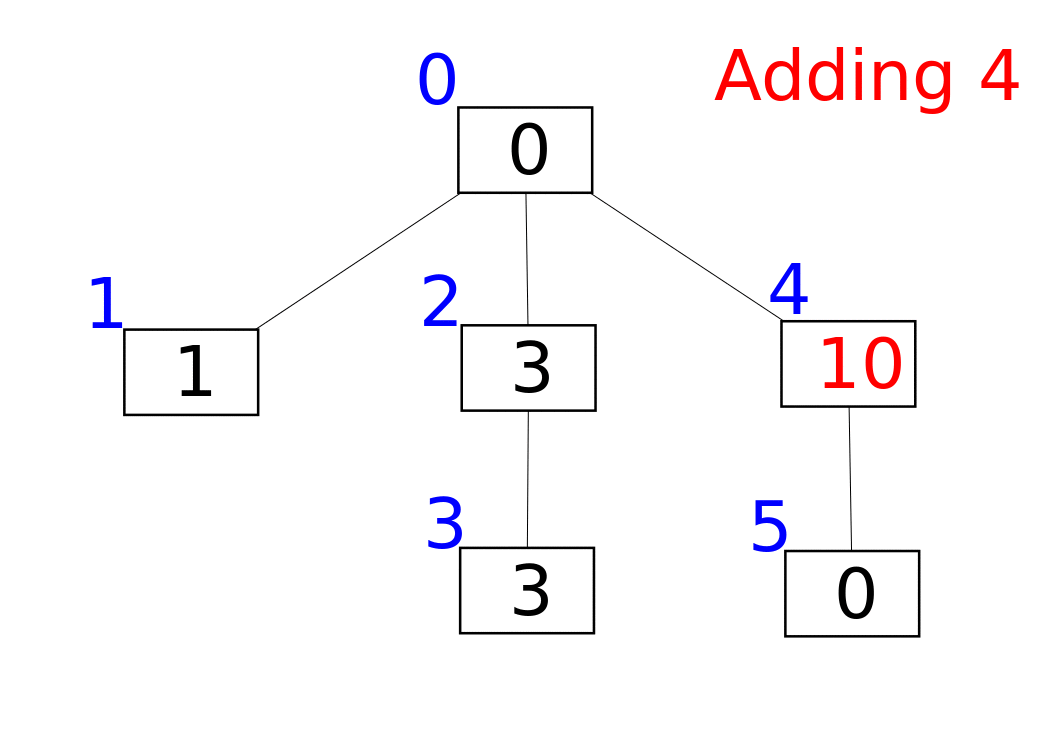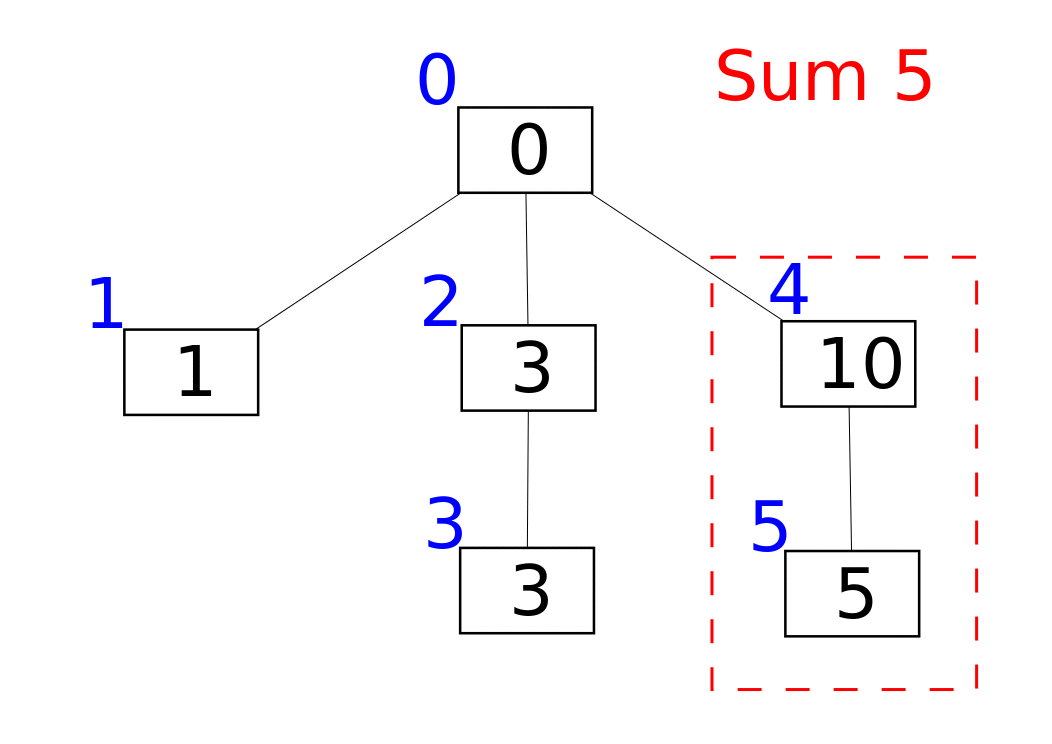
Структура представлена в виде массива f, в котором f[i] – сумма всех элементов от F[i] до i. Функция F(x) связана с битовым представлением аргумента. Вкратце можно описать так: F(x) заменяет группу единичных битов, находящихся в конце числа (младших) на нули. Если x заканчивается на нулевой бит, то F(x) = x. В битовых операциях F(x) задаётся так: F(x) = x & (x + 1).
Нам понадобятся три функции: прибавление x к элементу с индексом i, получение суммы дерева от 0 до x и получение суммы на [a..b].
Полный код дерева:
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
using namespace std;
const int SIZE = 100100;
int a[SIZE];
int f[SIZE];
void add (int i, int x, int n)
{
a[i] += x;
for (; i < n; i |= i + 1) f[i] += x;
}
int summary(int x)
{
int result = 0;
for (; x >= 0; x = (x & (x + 1)) - 1)
{
result += f[x];
}
return result;
}
int summary(int l, int r)
{
if (l)
{
return summary(r) - summary(l);
}
else
{
return summary(r);
}
}
int main()
{
int n;
cin >> n;
forn (i, n)
{
int val;
cin >> val;
add(i, val, n);
}
int q;
cin >> q;
forn (r, q)
{
string type;
cin >> type;
if (type == "1")
{
int i, x;
cin >> i >> x;
--i;
add(i, x, n);
}
else if (type == "2")
{
int a, b;
cin >> a >> b;
--a; --b;
cout << summary(a, b) << "\n";
}
}
return 0;
}
Задачи на sparse table
Задачи на дерево Фенвика




Комментарии