Представьте, что вы проходите техническое собеседование в IT-компанию. Вопросы — один другого сложнее: алгоритмы, структуры данных, архитектурные паттерны, лучшие практики... Важно не растеряться, не потерять направление. Именно в такие моменты нужно держать в голове свой внутренний «вектор» — то, что помогает не сбиться с курса. В математике и машинном обучении есть очень похожее понятие — собственный вектор. Это направление, которое сохраняется даже после преобразования данных. Метод главных компонент, или PCA, как раз опирается на собственные векторы и собственные значения, чтобы упростить многомерные данные, не потеряв суть.
Что такое PCA и зачем он нужен
PCA (Principal Component Analysis, метод главных компонент) — это способ снижения размерности данных. Дата-сайентисты часто работают с многомерными наборами данных, содержащими сотни и тысячи признаков, особенно если задачи связаны с финансами, биоинформатикой или компьютерным зрением. Огромный объем сильно усложняет понимание структуры данных, и делает визуализацию почти невыполнимой задачей. Здесь-то и приходит на помощь метод PCA. Он позволяет:
- Упростить модель, оставив только наиболее значимые признаки.
- Удалить избыточную информацию (коррелированные признаки).
- Понятно визуализировать данные в 2D или 3D.
И все это благодаря собственным значениям и собственным векторам матрицы ковариаций признаков.
Что такое собственные векторы, собственные значения и главные компоненты
Представим, что у нас есть матрица данных. Мы хотим понять, какие направления в этих данных самые важные — то есть найти векторы, вдоль которых разброс максимален. Именно эти направления будут собственными векторами матрицы ковариации. Их значимость определяется соответствующими собственными значениями — чем больше значение, тем больше информации несет этот вектор. Собственные векторы ковариационной матрицы, упорядоченные по убыванию соответствующих собственных значений, называются главными компонентами:
- Первая главная компонента соответствует направлению максимальной вариации данных.
- Вторая главная компонента соответствует направлению максимальной вариации, перпендикулярному первой компоненте.
- И так далее.
Если продолжить аналогию с поведением кандидата на собеседовании в IT компании, когда он демонстрирует уверенность и опирается на свои сильные стороны — именно эти личные качества и становятся его главными компонентами.
Практическая задача: анализ доходностей S&P 500
Предположим, вы пришли на собеседование в IT-компанию, и вам дают задание — провести анализ доходностей акций, входящих в индекс S&P 500:
- Информация представляет собой ежедневные логарифмические доходности закрытия для 453 акций, входящих в индекс. Ежедневная логарифмическая доходность — это натуральный логарифм отношения цены закрытия акции к цене закрытия предыдущего торгового дня: log_return = ln(цена_сегодня / цена_вчера).
- Данные охватывают трехлетний период (1258 точек наблюдения) и находятся в csv-файле.
- Акции представлены в виде столбцов и обозначены как S1, S2, ..., S453.
- Временные точки представлены в виде строк.
В вашем распоряжении Python и все нужные библиотеки — NumPy, pandas, scikit-learn и matplotlib. Требуется:
- Выяснить, сколько главных компонент объясняют большую часть дисперсии.
- Построить графики.
- Интерпретировать результаты.
📥 Шаг 1: Импортируем библиотеки, загружаем данные
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
sp500_returns = pd.read_csv('SP500_log_returns.csv')
Можно вывести первые строки датасета и базовую статистическую информацию о данных:
print(sp500_returns.head(10))
print(sp500_returns.describe())
Результат:
S1 S2 S3 ... S451 S452 S453
0 -0.002871 0.010870 0.002714 ... -0.000855 0.029694 0.011900
1 -0.008043 -0.042482 -0.001026 ... -0.004280 0.038409 0.009737
2 0.000000 0.039669 -0.016034 ... -0.006603 0.092847 -0.002581
3 0.000974 0.005433 -0.005541 ... 0.004042 0.108162 0.007450
4 0.005208 0.033456 0.007957 ... 0.000576 0.013497 0.002908
5 -0.001945 -0.002290 -0.012722 ... 0.012536 0.002426 0.015267
6 -0.003606 -0.037931 -0.007052 ... 0.013427 -0.020352 -0.016914
7 0.007194 0.013229 0.013285 ... 0.001673 0.024769 0.004647
8 0.018141 -0.011321 -0.003242 ... 0.010251 0.021168 0.005275
9 -0.025630 -0.008283 -0.023990 ... -0.016681 -0.031480 -0.011913
[10 rows x 453 columns]
S1 S2 ... S452 S453
count 1258.000000 1258.000000 ... 1258.000000 1258.000000
mean 0.000403 -0.000900 ... 0.000345 0.000588
std 0.016390 0.017143 ... 0.018901 0.011595
min -0.085039 -0.083011 ... -0.083008 -0.048150
25% -0.007775 -0.010467 ... -0.009978 -0.006124
50% 0.000685 -0.000723 ... 0.000473 0.001025
75% 0.009782 0.009167 ... 0.010233 0.007531
max 0.075508 0.078886 ... 0.108162 0.053471
🧠 Шаг 2: Создаем и обучаем PCA-объект
PCA строит матрицу ковариации, извлекает из нее собственные значения и собственные векторы:
pca = PCA()
pca.fit(sp500_returns.to_numpy())
print(pca.singular_values_)
Результат:
[6.81525175 1.91949441 1.63241764 1.50134004 1.28434791 1.17872029
1.11610732 1.06846725 1.03932026 0.99546176 0.95140063 0.92466035
0.89785509 0.86505051 0.85204576 0.84138373 0.81049572 0.79682213
0.78443322 0.76384842 0.7484207 0.73717281 0.733476 0.7235442
0.71899968 0.71415532 0.7096338 0.70448876 0.69214041 0.68325691
0.67105932 0.66611113 0.66155025 0.65398 0.64621404 0.64512543
0.63996132 0.63838178 0.63470436 0.63153004 0.63005999 0.62730717
0.62463979 0.61671736 0.61372499 0.60363442 0.59999259 0.59743976
0.59610674 0.59281799 0.58978894 0.58752082 0.582829 0.57598085
0.57242566 0.57090863 0.56914176 0.56370125 0.56307904 0.56064567
0.55726742 0.55557199 0.55338438 0.55311078 0.54599811 0.54471752
0.54322518 0.53820444 0.53379775 0.53139146 0.52937472 0.52644879
0.52309372 0.51934747 0.51549387 0.51401251 0.51145427 0.50926938
0.50775704 0.50646089 0.5030845 0.50081497 0.50025327 0.49833602
0.49626551 0.49380557 0.49243176 0.48761767 0.48646078 0.48379614
0.48204823 0.4808007 0.47923833 0.47727081 0.47466696 0.47348619
0.46966487 0.46820569 0.46435598 0.46360241 0.4618755 0.46072133
0.45870863 0.45642343 0.45451769 0.45290182 0.45233709 0.4512607
0.44832845 0.44682215 0.4453711 0.44272386 0.44156266 0.43807039
0.43768106 0.4349368 0.43338005 0.4322535 0.43184166 0.42981318
0.42841936 0.42713364 0.42408653 0.4229342 0.42131799 0.42013017
0.41946629 0.41844898 0.41583619 0.41541156 0.4126558 0.4111266
0.40973268 0.40854031 0.40777759 0.40692228 0.40576469 0.40490767
0.40214346 0.40105319 0.39933893 0.39744001 0.39638801 0.39417847
0.39269789 0.39159571 0.39050045 0.3901582 0.38762315 0.38679407
0.38546525 0.38317441 0.38180877 0.38011499 0.37907541 0.37822393
0.37736131 0.37663171 0.37608348 0.37196589 0.37096899 0.36951655
0.36856845 0.36728372 0.36472062 0.36400392 0.36343077 0.36117823
0.36004955 0.35915671 0.35748667 0.35696768 0.35601592 0.35521415
0.35349609 0.35297569 0.35124654 0.35069776 0.34892328 0.34801833
0.34703851 0.34659874 0.34491778 0.34412156 0.34208497 0.34070238
0.33949521 0.33780139 0.33659661 0.33611766 0.33440196 0.33342094
0.33248888 0.33149803 0.33018624 0.32833341 0.32760555 0.32741304
0.32633023 0.32380416 0.32338067 0.3219539 0.32130483 0.31999653
0.31938478 0.31877772 0.3180783 0.31631707 0.31439067 0.31357091
0.31256526 0.3108602 0.30932996 0.30786799 0.307016 0.30656068
0.30542521 0.30529616 0.30403405 0.30186992 0.30176511 0.30081254
0.29988928 0.29943916 0.29823801 0.29744369 0.29625549 0.29527815
0.29499574 0.29441594 0.29233187 0.29218714 0.29096529 0.29026243
0.28936697 0.28894191 0.28725714 0.28691464 0.28624131 0.28418529
0.28394829 0.28387552 0.28195903 0.27966374 0.27884562 0.27818351
0.27768815 0.27651108 0.2751642 0.27497319 0.27343806 0.27263282
0.2723583 0.27059244 0.26970414 0.26853053 0.26729327 0.26598458
0.26565372 0.26444162 0.26404856 0.26328932 0.26257496 0.26235913
0.26056223 0.26023626 0.25994767 0.25952443 0.25703889 0.25662728
0.25638238 0.25449574 0.25338661 0.25290235 0.252475 0.25179394
0.25132948 0.24999946 0.24950583 0.24810773 0.24691295 0.24643749
0.24538295 0.24420597 0.24336445 0.24298677 0.24202827 0.24071353
0.24000471 0.23914488 0.23818455 0.23720874 0.23693193 0.23550601
0.23493863 0.23474086 0.233809 0.23266014 0.23102998 0.23015823
0.22941854 0.22851853 0.22765141 0.22690214 0.22592864 0.22547522
0.22444907 0.22326967 0.22244206 0.22141922 0.22070004 0.2198815
0.21848497 0.2179842 0.21707391 0.2168834 0.21545595 0.21501635
0.21414278 0.21299696 0.21286583 0.21154378 0.21065965 0.20960921
0.20913919 0.20835033 0.20801349 0.20719669 0.20622314 0.20565166
0.2053846 0.2036775 0.20353077 0.20270214 0.2015156 0.20058159
0.19996921 0.19942632 0.19845352 0.19806244 0.19671856 0.19643745
0.19522727 0.19440685 0.19330599 0.19247893 0.19125242 0.19038354
0.19021076 0.18910676 0.1888695 0.18798691 0.1877339 0.18706179
0.18567659 0.18509977 0.18469602 0.18379356 0.18356232 0.18157656
0.18071367 0.17983357 0.17952306 0.17865637 0.17773235 0.17746082
0.176258 0.1747647 0.17453443 0.17431018 0.17349672 0.17266998
0.17120491 0.17059613 0.17010228 0.16754764 0.16709587 0.16635361
0.1659833 0.16487767 0.16455164 0.16244392 0.16193444 0.16180908
0.16107754 0.15953354 0.15892702 0.15822591 0.15763544 0.1566846
0.15642225 0.15596316 0.1547844 0.15465616 0.15288093 0.15147808
0.15098146 0.1507587 0.15034366 0.14943948 0.14843622 0.14711504
0.14572282 0.14540683 0.14435441 0.14417114 0.14312968 0.14185972
0.14155741 0.14072545 0.13919771 0.13876269 0.13775849 0.13672928
0.13609117 0.1354713 0.13488639 0.13411416 0.13329722 0.13263402
0.13229735 0.13096094 0.13004236 0.12972902 0.12930004 0.12751855
0.12689856 0.12483105 0.12393164 0.12337543 0.12310416 0.12165867
0.12119055 0.11991168 0.11871322 0.11823971 0.11641337 0.11547039
0.11367846 0.11271986 0.11180571 0.11120156 0.11013007 0.10685891
0.10647197 0.10547043 0.10407303 0.10270361 0.10114247 0.09918176
0.09572909 0.09432036 0.08850963]
📈 Шаг 3: Строим график кумулятивной объясненной дисперсии
Чтобы понять, сколько компонент стоит сохранить, посмотрим на кумулятивную долю объясненной дисперсии:
pc_variance = np.power(pca.singular_values_, 2.0)
total_variance = np.sum(pc_variance)
cumulative_variance = 100.0 * np.cumsum(pc_variance) / total_variance
plt.plot(np.arange(1, 21), cumulative_variance[0:20], color='b', marker='o')
plt.title('Кумулятивная дисперсия, объяснeнная первыми 20 главными компонентами')
plt.xlabel('Главная компонента')
plt.ylabel('Кумулятивный % от общей дисперсии')
plt.show()
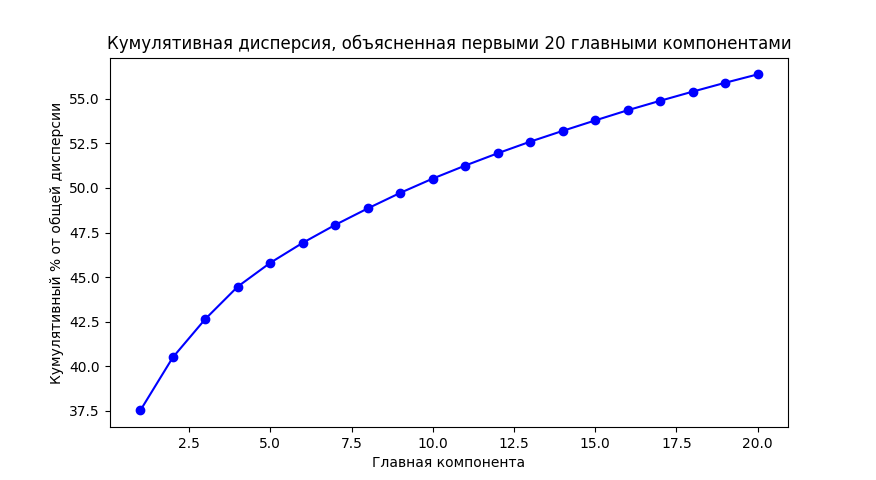
На графике вы увидите, сколько информации захватывают первые компоненты. Если, например, первые 5 компонент объясняют 90% дисперсии — значит, можно сократить размерность со 100 до 5 без существенной потери информации. По той же аналогии с собеседованием в IT — если вы хорошо знаете 5 ключевых технологий какого-то стека, то уже производите сильное впечатление.
В нашем случае первая главная компонента PC1 объясняет почти 38% общей дисперсии в этих данных. Это значит, что одно направление (собственный вектор) в многомерном пространстве уже содержит в себе более трети всей информации.
📊 Шаг 4: Интерпретируем нагрузку главной компоненты
Теперь посмотрим, какие акции сильнее всего влияют на первую главную компоненту:
plt.rcParams["figure.figsize"] = (20,6)
plt.stem(np.arange(1, pca.components_.shape[1] + 1), np.abs(pca.components_[0, :]), markerfmt=' ')
plt.title('Значения нагрузок для PC1', fontsize=24)
plt.xlabel('Акция', fontsize=20)
plt.ylabel('Нагрузка', fontsize=20)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.show()
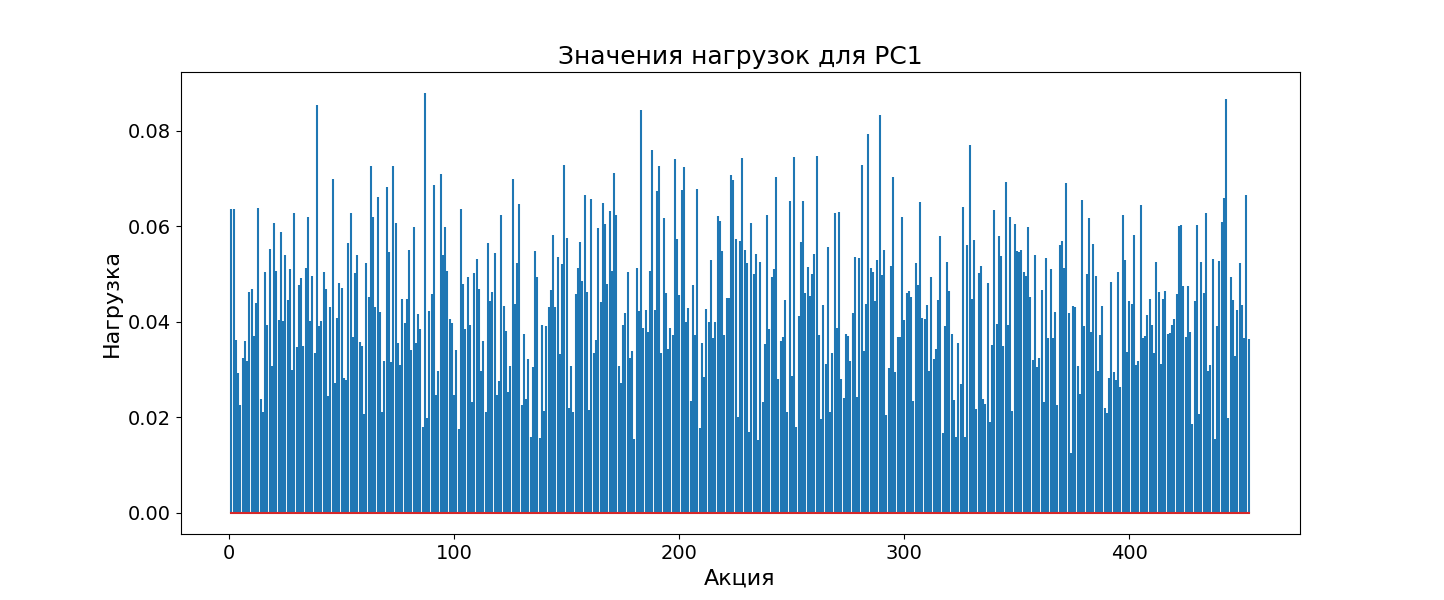
График нагрузок для первой главной компоненты PC1 показывает, насколько сильно каждая акция влияет на общее направление вариации данных. На графике видно, что все значения нагрузок имеют одинаковый знак и примерно одинаковую величину. Это говорит о том, что все акции движутся в одном направлении и в одинаковой степени влияют на первую компоненту.
Такая ситуация называется рыночным режимом. Она отражает общее поведение рынка: когда рынок растет, в среднем растут почти все акции, и наоборот — при падении рынка стоимость большинства бумаг тоже снижается. Это как единый пульс, объединяющий все акции в одно целое. Первая главная компонента фиксирует именно общее движение рынка, и с аналитической точки зрения это не так уж интересно. Куда любопытнее посмотреть на другие главные компоненты, которые уже не отражают рыночный режим, а показывают более тонкие различия между акциями.
🔍 Шаг 5: Визуализируем скрытую структуру в данных
Чтобы увидеть эти тонкие различия, мы построим график, где по осям будут вторая и третья главные компоненты (PC2 и PC3). Для этого сначала нужно вычислить значения этих компонент для каждой акции. В библиотеке scikit-learn это делается с помощью метода .transform(), применяемого к исходным данным. Он как бы переводит все акции из старого пространства (где у нас были доходности) в новое — пространство главных компонент:
scores = pca.transform(sp500_returns.to_numpy())
plt.scatter(x=scores[:, 1], y=scores[:, 2])
pc2_var = round(100.0 * (pc_variance[1] / total_variance), 2)
pc3_var = round(100.0 * (pc_variance[2] / total_variance), 2)
plt.title('Значение PC3 по отношению к значению PC2', fontsize=18)
plt.xlabel(f'PC2: {pc2_var}%', fontsize=16)
plt.ylabel(f'PC3: {pc3_var}%', fontsize=16)
plt.xticks(fontsize=14, rotation=45)
plt.yticks(fontsize=14)
plt.show()
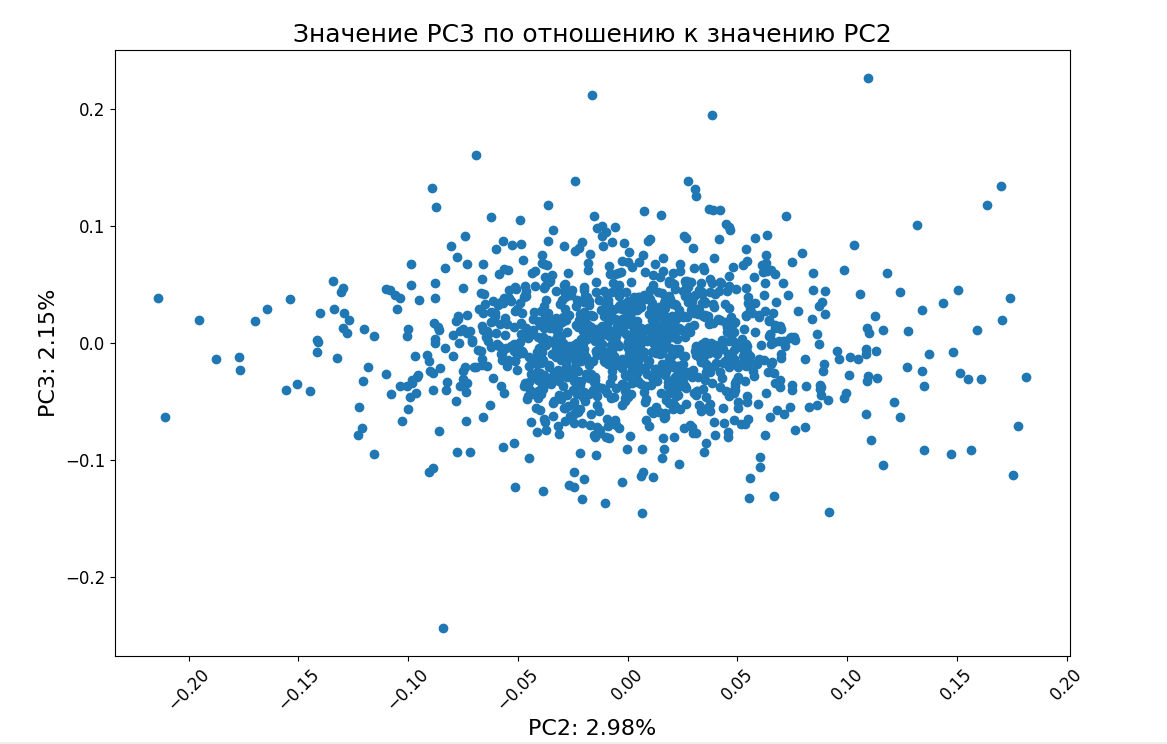
На графике видно, что PC2 и PC3 объясняют гораздо меньшую часть дисперсии, чем первая компонента PC1. Это говорит о том, что основное влияние на поведение акций оказывают глобальные рыночные факторы, которые затрагивают все компании сразу — например, общие экономические условия, процентные ставки, инфляция.
А вот вторая и третья компоненты (PC2 и PC3) скорее отражают локальные различия между группами акций — например, между предприятиями нефтегазового сектора и IT-компаниями. Эти компоненты могут захватывать поведение, характерное для конкретных индустрий. Если мы хотим точно понять, какие именно секторы лежат за PC2 и PC3, нужно посмотреть на нагрузки этих компонент. По тому, какие акции в них доминируют, можно понять, к какому сектору они относятся.
Решение задачи полностью:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
sp500_returns = pd.read_csv('SP500_log_returns.csv')
print(sp500_returns.head(10))
print(sp500_returns.describe())
pca = PCA()
pca.fit(sp500_returns.to_numpy())
print(pca.singular_values_)
pc_variance = np.power(pca.singular_values_, 2.0)
total_variance = np.sum(pc_variance)
cumulative_variance = 100.0 * np.cumsum(pc_variance) / total_variance
plt.plot(np.arange(1, 21), cumulative_variance[0:20], color='b', marker='o')
plt.title('Кумулятивная дисперсия, объяснeнная первыми 20 главными компонентами')
plt.xlabel('Главная компонента')
plt.ylabel('Кумулятивный % от общей дисперсии')
plt.show()
plt.rcParams["figure.figsize"] = (20,6)
plt.stem(np.arange(1, pca.components_.shape[1] + 1), np.abs(pca.components_[0, :]), markerfmt=' ')
plt.title('Значения нагрузок для PC1', fontsize=18)
plt.xlabel('Акция', fontsize=16)
plt.ylabel('Нагрузка', fontsize=16)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
scores = pca.transform(sp500_returns.to_numpy())
plt.scatter(x=scores[:, 1], y=scores[:, 2])
pc2_var = round(100.0 * (pc_variance[1] / total_variance), 2)
pc3_var = round(100.0 * (pc_variance[2] / total_variance), 2)
plt.title('Значение PC3 по отношению к значению PC2', fontsize=18)
plt.xlabel(f'PC2: {pc2_var}%', fontsize=16)
plt.ylabel(f'PC3: {pc3_var}%', fontsize=16)
plt.xticks(fontsize=12, rotation=45)
plt.yticks(fontsize=12)
plt.show()
Заключение
Метод главных компонент — это способ взглянуть на сложные данные под другим углом, вычленить суть, отбросив второстепенное. Как и на IT-собеседовании, где важно продемонстрировать ключевые навыки, PCA помогает выделить главные направления в данных — те, которые несут максимальную информацию. В нашем примере с акциями S&P 500 мы увидели, как одна компонента может отразить поведение всего рынка, а последующие — показать нюансы, скрытые от первого взгляда.
💡 Курс «Алгоритмы и структуры данных» от Proglib Academy
Хочешь уверенно проходить технические собеседования, развивать алгоритмическое мышление и писать более эффективный код? Приходи на курс! Тебя ждет интенсивная программа, созданная для разработчиков, которые хотят выйти на новый уровень: подготовиться к устройству в крупные IT-компании (Яндекс, Сбер, Google, Amazon и др.), научиться решать сложные задачи и систематизировать знания.
📌 Кому подходит курс:
- Junior-разработчикам и тем, кто хочет войти в IT.
- Middle-разработчикам — для прокачки алгоритмического мышления и подготовки к интервью.
- Всем, кто владеет хотя бы одним ООП-языком (Python, Java, C++, PHP, C#, JavaScript).
🎓 После прохождения ты:
- Научишься писать чистый, быстрый и эффективный код.
- Поймешь, как применять алгоритмы и структуры данных в реальных задачах.
- Освоишь методы оценки сложности кода (Big O).
- Смело пройдешь техническое интервью и получишь официальный сертификат, проверяемый на сайте Proglib Academy.
📚 Программа охватывает:
- Списки, очереди, стеки, деревья, графы, хеш-таблицы.
- Бинарный и линейный поиск, сортировки, динамическое программирование.
- Приоритетные очереди, жадные алгоритмы, строки и многое другое.
- Разбор задач с настоящих собеседований.
👨💻 Бонус — вебинары от практиков: например, мастер-класс от разработчика Яндекса Степана Мацкевича про очередь с приоритетом.



Комментарии