Описаны четыре популярных метода обучения без учителя для кластеризации данных с соответствующими примерами программного кода на Python.
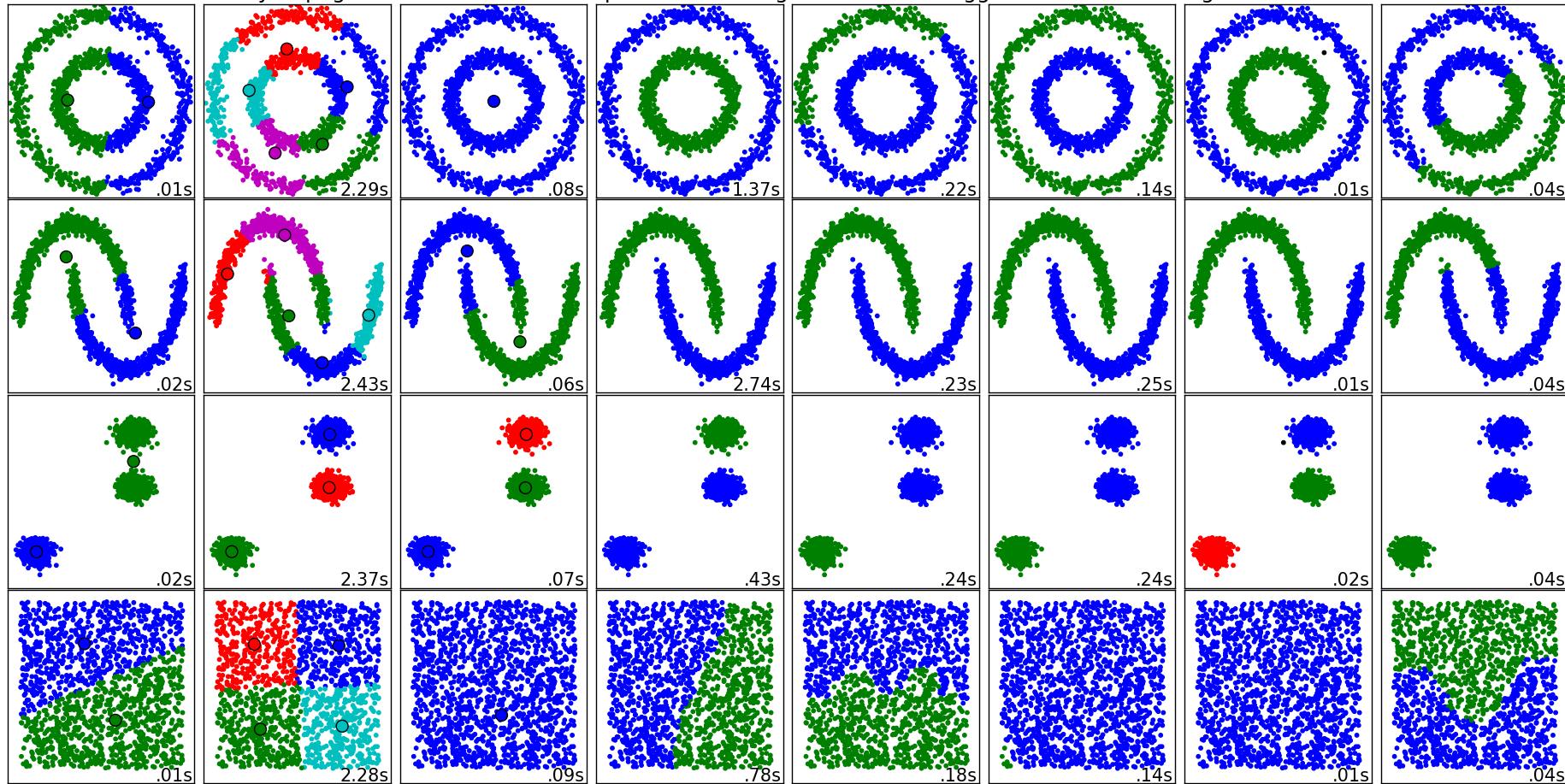
Обучение без учителя
Обучение без учителя (unsupervised learning, неконтролируемое обучение) – класс методов машинного обучения для поиска шаблонов в наборе данных. Данные, получаемые на вход таких алгоритмов обычно не размечены, то есть передаются только входные переменные X без соответствующих меток y. Если в контролируемом обучении (обучении с учителем, supervised learning) система пытается извлечь уроки из предыдущих примеров, то в обучении без учителя – система старается самостоятельно найти шаблоны непосредственно из приведенного примера.
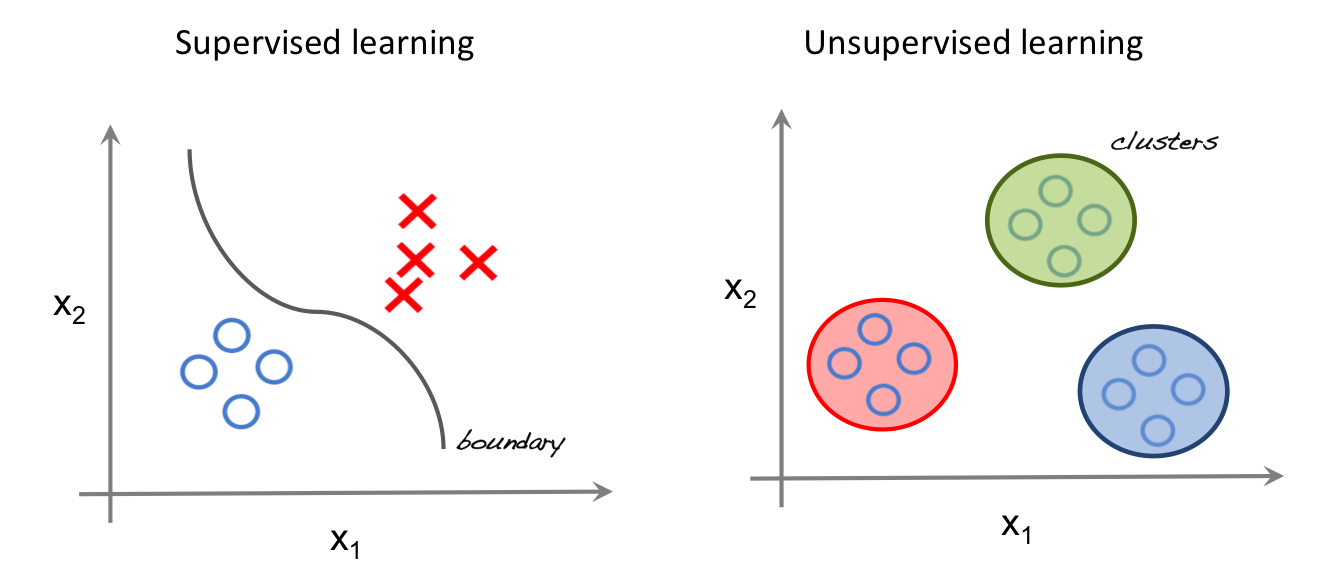
На левой части изображения представлен пример контролируемого обучения: здесь для того, чтобы найти лучшую функцию, соответствующую представленным точкам, используется метод регрессии. В то же время при неконтролируемом обучении входные данные разделяются на основе представленных характеристик, а предсказание свойств основывается на том, какому кластеру принадлежит пример.
Методы кластеризации данных являются одним из наиболее популярных семейств машинного обучения без учителя. Рассмотрим некоторые из них подробнее.
Важная терминология
- Feature (Особенности): входная переменная, используемая для создания прогнозов.
- Predictions (Прогнозы): выходные данные модели при наличии входного примера.
- Example (Пример): строка набора данных. Пример обычно содержит один или несколько объектов.
- Label (Метки): результат функции.
Подготовка выборки для кластеризации данных
Для составления прогнозов воспользуемся классическим набором данных ирисов Фишера. Датасет представляет набор из 150 записей с пятью атрибутами в следующем порядке: длина чашелистика (sepal length), ширина чашелистика (sepal width), длина лепестка (petal length), ширина лепестка (petal width) и класс, соответствующий одному из трех видов: Iris Setosa, Iris Versicolor или Iris Virginica, обозначенных соответственно 0, 1, 2. Наш алгоритм должен принимать четыре свойства одного конкретного цветка и предсказывать, к какому классу (виду ириса) он принадлежит. Имеющиеся в наборе данных метки можно использовать для оценки качества предсказания.
Для решения задач кластеризации данных в этой статье мы используем Python, библиотеку scikit-learn для загрузки и обработки набора данных и matplotlib для визуализации. Ниже представлен программный код для исследования исходного набора данных.
# Импортируем библиотеки from sklearn import datasets import matplotlib.pyplot as plt # Загружаем набор данных iris_df = datasets.load_iris() # Методы, доступные для набора данных print(dir(iris_df)) # Признаки print(iris_df.feature_names) # Метки print(iris_df.target) # Имена меток print(iris_df.target_names) # Разделение набора данных x_axis = iris_df.data[:, 0] # Sepal Length y_axis = iris_df.data[:, 1] # Sepal Width # Построение plt.xlabel(iris_df.feature_names[0]) plt.ylabel(iris_df.feature_names[1]) plt.scatter(x_axis, y_axis, c=iris_df.target) plt.show()
В результате запуска программы вы увидим следующие текст и изображение.
['DESCR', 'data', 'feature_names', 'target', 'target_names'] ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] ['setosa' 'versicolor' 'virginica']
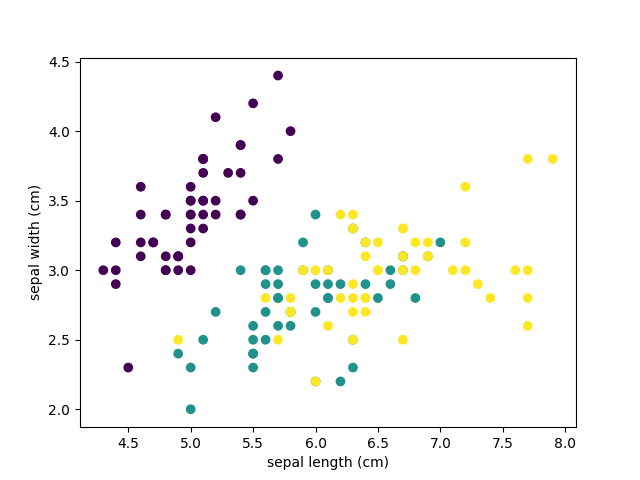
На диаграмме фиолетовым цветом обозначен вид Setosa, зеленым – Versicolor и желтым – Virginica. При построении были взяты лишь два признака. Вы можете проанализировать как разделяются классы при других комбинациях параметров.
Цель кластеризации данных состоит в том, чтобы выделить группы примеров с похожими чертами и определить соответствие примеров и кластеров. При этом исходно у нас нет примеров такого разбиения. Это аналогично тому, как если бы в приведенном наборе данных у нас не было меток, как на рисунке ниже.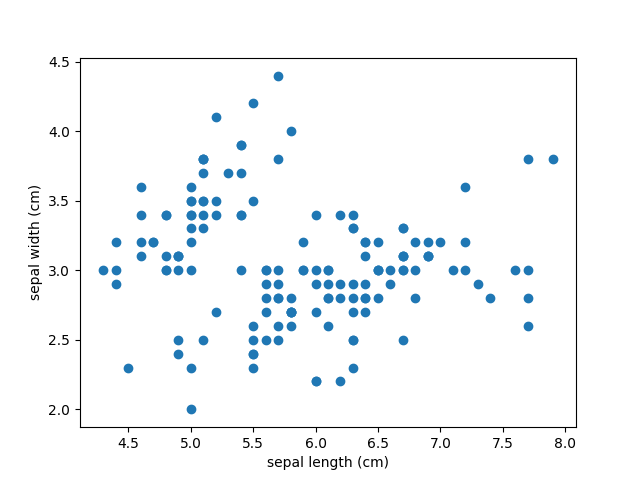
Наша задача – используя все имеющиеся данные, предсказать соответствие объектов выборки их классам, сформировав таким образом кластеры.
Метод k-средних
Наиболее популярным алгоритмом кластеризации данных является метод k-средних. Это итеративный алгоритм кластеризации, основанный на минимизации суммарных квадратичных отклонений точек кластеров от центроидов (средних координат) этих кластеров.
Первоначально выбирается желаемое количество кластеров. Поскольку нам известно, что в нашем наборе данных есть 3 класса, установим параметр модели n_clusters равный трем.
Теперь случайным образом из входных данных выбираются три элемента выборки, в соответствие которым ставятся три кластера, в каждый из которых теперь включено по одной точке, каждая при этом является центроидом этого кластера.
Далее ищем ближайшего соседа текущего центроида. Добавляем точку к соответствующему кластеру и пересчитываем положение центроида с учетом координат новых точек. Алгоритм заканчивает работу, когда координаты каждого центроида перестают меняться. Центроид каждого кластера в результате представляет собой набор значений признаков, описывающих усредненные параметры выделенных классов.
# Импортируем библиотеки from sklearn import datasets from sklearn.cluster import KMeans # Загружаем набор данных iris_df = datasets.load_iris() # Описываем модель model = KMeans(n_clusters=3) # Проводим моделирование model.fit(iris_df.data) # Предсказание на единичном примере predicted_label = model.predict([[7.2, 3.5, 0.8, 1.6]]) # Предсказание на всем наборе данных all_predictions = model.predict(iris_df.data) # Выводим предсказания print(predicted_label) print(all_predictions)
Результат:
[1] [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2 2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 2 2 0 2 2 0]
При выводе данных нужно понимать, что алгоритм не знает ничего о нумерации классов, и числа 0, 1, 2 – это лишь номера кластеров, определенных в результате работы алгоритма. Так как исходные точки выбираются случайным образом, вывод будет несколько меняться от одного запуска к другому.
Характерной особенностью набора данных ирисов Фишера является то, что один класс (Setosa) легко отделяется от двух остальных. Это заметно и в приведенном примере.
Иерархическая кластеризация
Иерархическая кластеризация, как следует из названия, представляет собой алгоритм, который строит иерархию кластеров. Этот алгоритм начинает работу с того, что каждому экземпляру данных сопоставляется свой собственный кластер. Затем два ближайших кластера объединяются в один и так далее, пока не будет образован один общий кластер.
Результат иерархической кластеризации может быть представлен с помощью дендрограммы. Рассмотрим этот тип кластеризации на примере данных для различных видов зерна.
# Импортируем библиотеки
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import pandas as pd
# Создаем датафрейм
seeds_df = pd.read_csv(
"http://qps.ru/jNZUT")
# Исключаем информацию об образцах зерна, сохраняем для дальнейшего использования
varieties = list(seeds_df.pop('grain_variety'))
# Извлекаем измерения как массив NumPy
samples = seeds_df.values
# Реализация иерархической кластеризации при помощи функции linkage
mergings = linkage(samples, method='complete')
# Строим дендрограмму, указав параметры удобные для отображения
dendrogram(mergings,
labels=varieties,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()
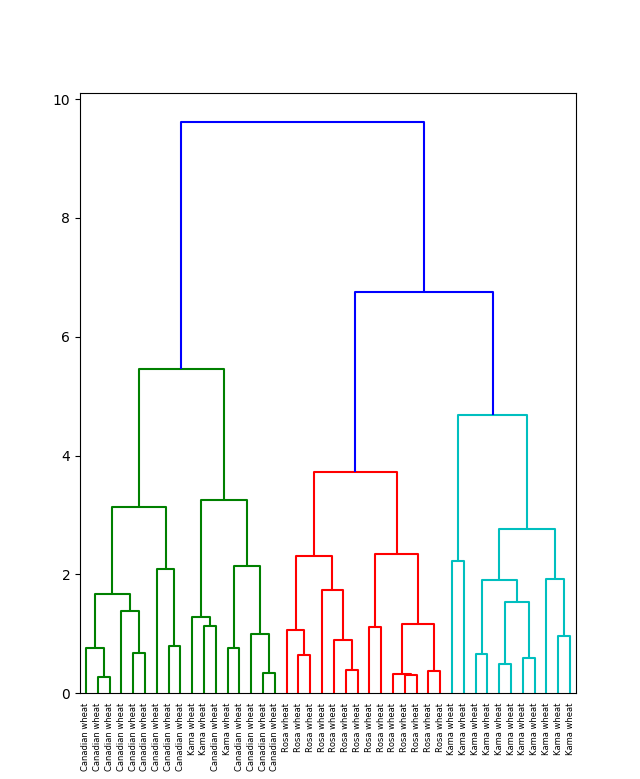
Можно видеть, что в результате иерархической кластеризации данных естественным образом произошло разбиение на три кластера, обозначенных на рисунке различным цветом. При этом исходно число кластеров не задавалось.
Сравнение метода k-средних с иерархической кластеризацией данных
- Иерархическая кластеризация хуже подходит для кластеризации больших объемов данных в сравнении с методом k-средних. Это объясняется тем, что временная сложность алгоритма линейна для метода k-средних (O(n)) и квадратична для метода иерархической кластеризации (O(n2))
- В кластеризации при помощи метода k-средних алгоритм начинает построение с произвольного выбора начальных точек, поэтому, результаты, генерируемые при многократном запуске алгоритма, могут отличаться. В то же время в случае иерархической кластеризации результаты воспроизводимы.
- Из центроидной геометрии построения метода k-средних следует, что метод хорошо работает, когда форма кластеров является гиперсферической (например, круг в 2D или сфера в 3D).
- Метод k-средних более чувствителен к зашумленным данным, чем иерархический метод.
Понижение размерности с методом t-SNE
Метод t-SNE (t-distributed stochastic neighbor embedding) представляет собой один из методов обучения без учителя, используемых для визуализации, например, отображения пространства высокой размерности в двух- или трехмерное пространство. t-SNE расшифровывается как распределенное стохастическое соседнее вложение.
Метод моделирует каждый объект пространства высокой размерности в двух- или трехкоординатную точку таким образом, что близкие по характеристикам элементы данных в многомерном пространстве (например, датасете с большим числом столбцов) проецируются в соседние точки, а разнородные объекты с большей вероятностью моделируются точками, далеко отстоящими друг от друга. Математическое описание работы метода можно найти здесь.
Вернемся к примеру с ирисами и посмотрим, как произвести моделирование по этому методу при помощи библиотеки sklearn.
# Импорт библиотек from sklearn import datasets from sklearn.manifold import TSNE import matplotlib.pyplot as plt # Загрузка датасета iris_df = datasets.load_iris() # Определяем модель и скорость обучения model = TSNE(learning_rate=100) # Обучаем модель transformed = model.fit_transform(iris_df.data) # Представляем результат в двумерных координатах x_axis = transformed[:, 0] y_axis = transformed[:, 1] plt.scatter(x_axis, y_axis, c=iris_df.target) plt.show()
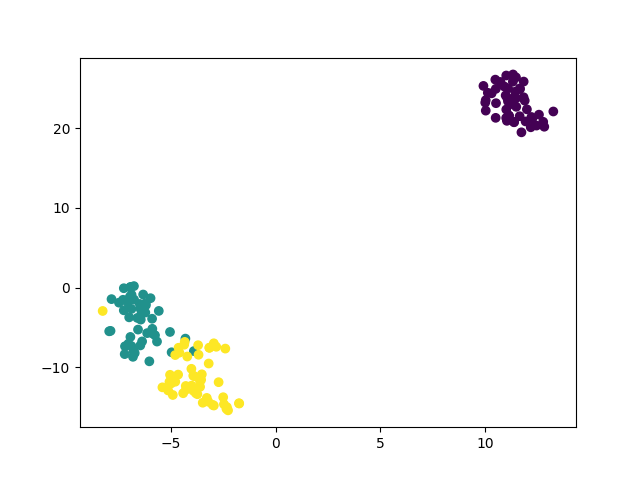
В этом случае каждый экземпляр представлен четырьмя координатами – таким образом, при отображении признаков на плоскость размерность пространства понижается с четырех до двух.
Метод кластеризации на основе плотности DBSCAN
DBSCAN (Density-Based Spatial Clustering of Applications with Noise, плотностной алгоритм пространственной кластеризации с присутствием шума) – популярный алгоритм кластеризации, используемый в анализе данных в качестве одной из замен метода k-средних.
Метод не требует предварительных предположений о числе кластеров, но нужно настроить два других параметра: eps и min_samples. Данные параметры – это соответственно максимальное расстояние между соседними точками и минимальное число точек в окрестности (количество соседей), когда можно говорить, что эти экземпляры данных образуют один кластер. В scikit-learn есть соответствующие значения параметров по умолчанию, но, как правило, их приходится настраивать самостоятельно.
# Импортируем библиотеки
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA
# Загружаем датасет
iris = load_iris()
# Определяем модель
dbscan = DBSCAN()
# Обучаем
dbscan.fit(iris.data)
# Уменьшаем размерность при помощи метода главных компонент
pca = PCA(n_components=2).fit(iris.data)
pca_2d = pca.transform(iris.data)
# Строим в соответствии с тремя классами
for i in range(0, pca_2d.shape[0]):
if dbscan.labels_[i] == 0:
c1 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='r', marker='+')
elif dbscan.labels_[i] == 1:
c2 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='g', marker='o')
elif dbscan.labels_[i] == -1:
c3 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='b', marker='*')
plt.legend([c1, c2, c3], ['Кластер 1', 'Кластер 2', 'Шум'])
plt.title('DBSCAN нашел 2 кластера и шум')
plt.show()
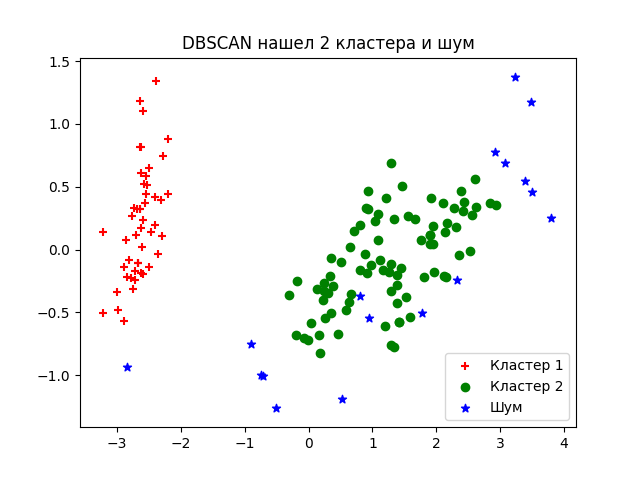
Об устройстве алгоритма простыми словами и о математической подноготной можно прочитать в этой статье.




Комментарии