Представьте, что вам нужно обработать данные о росте студентов-первокурсников из нескольких различных вузов. Среднее значение даст вам общее представление о выборке, но не расскажет, насколько разнообразны ваши данные. Вот тут на помощь и приходит математическая дисперсия — мера разброса значений вокруг среднего.
Что такое дисперсия
Дисперсия случайной величины показывает, насколько сильно ее значения отклоняются от математического ожидания (среднего значения). Чем больше дисперсия, тем сильнее варьируются данные. Низкая дисперсия указывает на то, что значения сгруппированы вокруг среднего. Звучит сложно? Давайте разберем по шагам, как вычислить дисперсию:
- Находим среднее значение наших данных.
- Для каждого значения вычисляем его отклонение от среднего.
- Возводим каждое отклонение в квадрат (чтобы отрицательные отклонения не компенсировали положительные).
- Находим среднее значение этих квадратов отклонений.
Математически это можно записать так:
Где E[X] — математическое ожидание (среднее значение) случайной величины X.
Квадратный корень из дисперсии называется стандартным отклонением σ. Это более наглядная характеристика, которая измеряется в тех же единицах, что и сама случайная величина. Проиллюстрируем вычисление дисперсии на небольшой выборке из 10 студентов, рост которых равен 165, 172, 180, 168, 175, 170, 182, 178, 166, 174 см:
- Находим среднее значение роста:
(165 + 172 + 180 + 168 + 175 + 170 + 182 + 178 + 166 + 174) / 10 = 1730 / 10 = 173 см
- Для каждого значения вычисляем отклонение от среднего:
Отклонение для 165 см: 165 - 173 = -8 см
Отклонение для 172 см: 172 - 173 = -1 см
Отклонение для 180 см: 180 - 173 = +7 см
Отклонение для 168 см: 168 - 173 = -5 см
Отклонение для 175 см: 175 - 173 = +2 см
Отклонение для 170 см: 170 - 173 = -3 см
Отклонение для 182 см: 182 - 173 = +9 см
Отклонение для 178 см: 178 - 173 = +5 см
Отклонение для 166 см: 166 - 173 = -7 см
Отклонение для 174 см: 174 - 173 = +1 см
- Возводим каждое отклонение в квадрат:
(-8)² = 64
(-1)² = 1
(+7)² = 49
(-5)² = 25
(+2)² = 4
(-3)² = 9
(+9)² = 81
(+5)² = 25
(-7)² = 49
(+1)² = 1
- Находим среднее значение квадратов отклонений (дисперсию):
Дисперсия = (64 + 1 + 49 + 25 + 4 + 9 + 81 + 25 + 49 + 1) / 10 = 308 / 10 = 30,8 см²
Итак, дисперсия нашей выборки составляет 30,8 см², и это значит, что в среднем значения роста отклоняются от среднего значения (173 см) примерно на √30,8 ≈ 5,5 см. Этот пример наглядно демонстрирует, что несмотря на то, что средний рост студентов составляет 173 см, реальные значения варьируются в некотором диапазоне вокруг этого среднего.
Вычисление дисперсии в NumPy
На Питоне большие наборы данных удобно обрабатывать с помощью numpy.var(). Предположим, у нас есть данные о росте 3000 студентов 5 различных факультетов из 6 вузов:
student_id,height,age,birth_date,faculty,university
1,173,19,2005-06-14,Информатика,вуз-2
2,176,18,2006-04-24,Химия,вуз-2
3,185,19,2005-11-11,Физика,вуз-4
4,184,17,2007-05-19,Математика,вуз-2
5,189,19,2005-11-22,Биология,вуз-4
.......
2994,185,18,2006-12-03,Информатика,вуз-1
2995,169,19,2005-03-28,Информатика,вуз-4
2996,168,19,2005-08-17,Химия,вуз-5
2997,185,17,2007-11-25,Математика,вуз-5
2998,164,19,2005-10-24,Информатика,вуз-3
2999,180,19,2005-02-06,Биология,вуз-6
3000,167,17,2007-11-08,Химия,вуз-2
Код будет выглядеть так:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("students_data.csv")
# Оценка дисперсии роста
variance = np.var(df["height"])
print(f"Дисперсия роста студентов: {variance:.2f}")
# Среднее значение и стандартное отклонение
mean_height = df["height"].mean()
std_height = np.sqrt(variance)
print(f"Средний рост студентов: {mean_height:.2f} см")
print(f"Стандартное отклонение: {std_height:.2f} см")
plt.figure(figsize=(10, 5))
plt.hist(df["height"], bins=15, color="skyblue", edgecolor="black", alpha=0.7)
plt.axvline(mean_height, color="red", linestyle="dashed", linewidth=2, label="Средний рост")
plt.axvline(mean_height + std_height, color="green", linestyle="dotted", linewidth=1.5,
label="±1 Стандартное отклонение")
plt.axvline(mean_height - std_height, color="green", linestyle="dotted", linewidth=1.5)
plt.xlabel("Рост (см)")
plt.ylabel("Количество студентов")
plt.title("Распределение роста студентов")
plt.legend()
plt.grid(axis="y", alpha=0.3)
plt.show()
students_within_std = df[(df["height"] >= mean_height - std_height) &
(df["height"] <= mean_height + std_height)]
percentage = len(students_within_std) / len(df) * 100
print(f"Процент студентов в пределах ±1 стандартного отклонения: {percentage:.2f}%")
Результат:
Дисперсия роста студентов: 80.83
Средний рост студентов: 174.76 см
Стандартное отклонение: 8.99 см
Процент студентов в пределах ±1 стандартного отклонения: 57.30%

Почему дисперсия важна для Data Science
В анализе данных и машинном обучении дисперсия играет ключевую роль по нескольким причинам:
- Оценка неопределенности. Дисперсия показывает, насколько надежны ваши данные и предсказания. Высокая дисперсия означает большую неопределенность.
- Выявление выбросов. Значения, которые значительно (обычно более чем на 3σ) отклоняются от среднего, могут считаться выбросами и требуют особого внимания.
- Сравнение распределений. Дисперсия позволяет сравнивать разные наборы данных, даже если их средние значения одинаковы.
- Нормализация данных. Знание дисперсии помогает стандартизировать данные, что улучшает работу многих алгоритмов машинного обучения.
- Баланс между смещением и дисперсией. Это ключевая концепция в машинном обучении, о которой мы поговорим подробнее ниже.
Дисперсия в машинном обучении
В машинном обучении дисперсия используется для оценки ошибок модели. Ошибку предсказания модели можно разложить на три компонента:
Ошибка = Смещение2 + Дисперсия + Шум
Где:
- Смещение — насколько среднее предсказание модели отличается от истинных значений.
- Дисперсия — насколько сильно меняются предсказания модели при изменении обучающей выборки.
- Шум — случайные ошибки, которые невозможно устранить.
Если дисперсия модели высокая, это значит, что модель сильно зависит от обучающих данных, что ведет к переобучению. Если дисперсия низкая, модель может быть слишком простой и не улавливать зависимости в данных (недообучение).
Гипотетически, идеальная модель должна одновременно иметь и низкое смещение, и низкую дисперсию, но на практике это невозможно, поэтому приходится искать баланс между ними. И здесь на помощь приходят ансамблевые методы, в первую очередь Random Forest.
Random Forest: как дисперсия помогает уменьшить ошибки
Random Forest («случайный лес») — это алгоритм машинного обучения, который использует ансамбль решающих деревьев. Каждое дерево в «лесу» обучается на случайной подвыборке данных и случайном подмножестве признаков. Конечный результат получается путем усреднения предсказаний всех деревьев (для регрессии) или голосования большинства (для классификации).
Но как это связано с дисперсией? Давайте разберемся:
1️⃣ Уменьшение дисперсии через усреднение. Отдельное решающее дерево может иметь высокую дисперсию — оно чувствительно к шуму в данных. Но когда мы усредняем результаты многих деревьев, дисперсия ошибки уменьшается. Это прямое следствие статистического принципа: дисперсия среднего значения n независимых случайных величин с одинаковой дисперсией σ² равна σ²/n.
2️⃣ Декорреляция деревьев. Чтобы усреднение было эффективным, деревья должны как можно меньше коррелировать между собой. Random Forest достигает этого двумя способами:
- Бутстрэп — каждое дерево строится на случайной подвыборке данных.
- Случайный выбор признаков — для каждого разбиения выбирается случайное подмножество признаков.
3️⃣ Баланс смещения и дисперсии. Отдельные деревья в Random Forest обычно выращиваются до максимальной глубины, что делает их склонными к переобучению (высокая дисперсия, низкое смещение). Но благодаря усреднению общая модель имеет умеренную дисперсию при сохранении низкого смещения: если предсказания разных моделей f1(x), f2(x), ..., fn(x) не сильно коррелированы, то дисперсия их усредненного предсказания уменьшается по закону:
Практические аспекты настройки Random Forest
Понимание роли дисперсии помогает настраивать Random Forest оптимальным образом:
- Количество деревьев. Увеличение числа деревьев уменьшает дисперсию, но с определенного момента улучшение становится незначительным. Обычно используют от 100 до 500 деревьев.
- Максимальная глубина деревьев. Глубокие деревья имеют низкое смещение, но высокую дисперсию. Ограничение глубины может помочь при наличии шума в данных.
- Минимальное количество образцов в листе. Увеличение этого параметра может уменьшить дисперсию за счет некоторого увеличения смещения.
- Максимальное количество признаков для разбиения. По умолчанию для регрессии в scikit-learn используется
n_features/3, а для классификации —sqrt(n_features). Увеличение этого параметра может уменьшить дисперсию, но увеличит корреляцию между деревьями. - Бутстрэп. Включение/выключение бутстрэпа влияет на разнообразие деревьев и, следовательно, на дисперсию.
Пример реализации Random Forest на Python
Сейчас мы разберем, как построить и улучшить модель машинного обучения на основе Random Forest. Мы будем использовать синтетический датасет с информацией о телефонных маркетинговых кампаниях, проведенных сотрудниками банка. Модель должна будет предсказать, выполнит ли клиент целевое действие, т.е. согласится ли на предложение банка открыть срочный счет.
Модель будет построена с использованием питоновской библиотеки scikit-learn, и мы пройдем полный путь от загрузки данных до настройки гиперпараметров и визуализации результатов. Набор синтетических данных сгенерирован с помощью этого кода:
import pandas as pd
import numpy as np
np.random.seed(42)
num_samples = 1000
age = np.random.randint(18, 80, num_samples)
balance = np.random.randint(-2000, 50000, num_samples)
duration = np.random.randint(50, 5000, num_samples)
campaign = np.random.randint(1, 10, num_samples)
previous = np.random.randint(0, 10, num_samples)
y = (balance > 5000).astype(int)
y[duration > 2000] = 1
y[campaign > 5] = 0
y[age > 60] = np.random.choice([0, 1], p=[0.3, 0.7], size=sum(age > 60))
bank_data = pd.DataFrame({
'возраст': age,
'баланс': balance,
'длительность': duration,
'кампания': campaign,
'предыдущие_контакты': previous,
'просрочка': np.random.choice([0, 1], num_samples, p=[0.85, 0.15]),
'целевой_ответ': y
})
bank_data.to_csv('bank_data.csv', index=False)
🧰 Шаг 1: Импортируем нужные библиотеки
Здесь мы импортируем библиотеки для работы с данными, построения модели и ее оценки, а также для визуализации деревьев и важности признаков:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.tree import plot_tree
from scipy.stats import randint
📥 Шаг 2: Загружаем данные
Датасет загружается в переменную bank_data:
bank_data = pd.read_csv("bank_data.csv")
Мы используем синтетические данные, которые не нуждаются в предварительной очистке, нормализации и кодировании признаков. Для реальных данных такая обработка и кодирование меток обязательны (например, необходимо представить целевую переменную и наличие просрочки численно, в виде 0 или 1).
🧪 Шаг 3: Разделяем данные на признаки и целевую переменную
X содержит все признаки, кроме целевого столбца, а y — это целевая переменная, которую мы хотим предсказывать:
X = bank_data.drop("целевой_ответ", axis=1)
y = bank_data["целевой_ответ"]
✂️ Шаг 4: Разделяем данные на обучающую и тестовую выборки
Модель обучается на 80% данных и проверяется на оставшихся 20%:
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
🔢Шаг 5: Определяем пространство гиперпараметров
Мы задаем диапазоны значений для двух гиперпараметров:
- n_estimators — количество деревьев в лесу.
- max_depth — максимальная глубина одного дерева.
param_dist = {
"n_estimators": randint(50, 500),
"max_depth": randint(1, 20)
}
🌲 Шаг 6: Создаем модель и подбираем гиперпараметры
- RandomizedSearchCV случайным образом перебирает 5 комбинаций гиперпараметров
n_iter=5. - Используется кросс-валидация на 5 фолдах
cv=5. - Обучение идет параллельно по всем ядрам CPU
n_jobs=-1.
rf = RandomForestClassifier(random_state=42)
rand_search = RandomizedSearchCV(
rf,
param_distributions=param_dist,
n_iter=5,
cv=5,
random_state=42,
n_jobs=-1
)
rand_search.fit(X_train, y_train)
🏆 Шаг 7: Выбираем лучшую модель
После подбора сохраняем лучшую модель и выводим параметры, при которых она показала наилучшие результаты:
best_rf = rand_search.best_estimator_
print(f"Лучшие гиперпараметры: {rand_search.best_params_}")
Результат:
Лучшие гиперпараметры: {'max_depth': 8, 'n_estimators': 238}
🧮 Шаг 8: Оцениваем качество модели
Здесь мы вычисляем и выводим:
- Accuracy — общее количество правильных предсказаний.
- Precision — долю истинных положительных среди всех предсказанных положительных.
- Recall — долю правильно предсказанных положительных среди всех истинных положительных.
y_pred = best_rf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average="binary")
recall = recall_score(y_test, y_pred, average="binary")
print(f"Общая точность, Accuracy: {accuracy:.3f}")
print(f"Точность положительного класса, Precision: {precision:.3f}")
print(f"Полнота, Recall: {recall:.3f}")
Результат:
Общая точность, Accuracy: 0.880
Точность положительного класса, Precision: 0.868
Полнота, Recall: 0.952
📊 Шаг 9: Визуализируем матрицу ошибок
Матрица ошибок помогает визуально оценить, насколько хорошо модель различает классы. Она особенно полезна при несбалансированных классах:
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm)
disp.plot(cmap="Blues")
plt.title("Матрица ошибок")
plt.show()
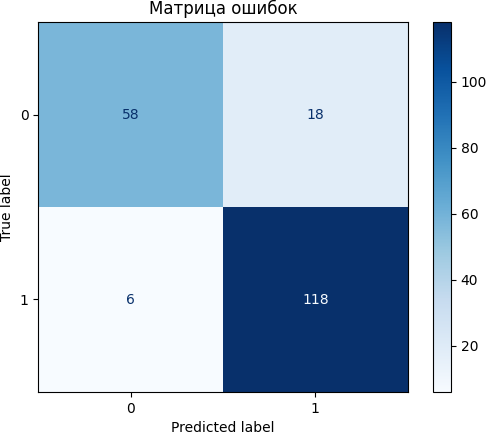
Матрица ошибок показывает, насколько хорошо модель классифицирует два класса (согласие или отказ клиентов от предложения открыть новый счет):
- True Negative (TN) = 58 – модель правильно предсказала класс 0.
- False Positive (FP) = 18 – модель ошибочно предсказала класс 1 вместо 0.
- False Negative (FN) = 6 – модель ошибочно предсказала класс 0 вместо 1.
- True Positive (TP) = 118 – модель правильно предсказала класс 1.
📈 Шаг 10: Визуализируем важность признаков
Эта визуализация позволяет понять, какие признаки сильнее всего повлияли на решения модели:
feature_importances = pd.Series(
best_rf.feature_importances_,
index=X_train.columns
).sort_values(ascending=False)
plt.figure(figsize=(10, 6))
feature_importances.plot.bar()
plt.title("Важность признаков")
plt.ylabel("Важность")
plt.tight_layout()
plt.show()
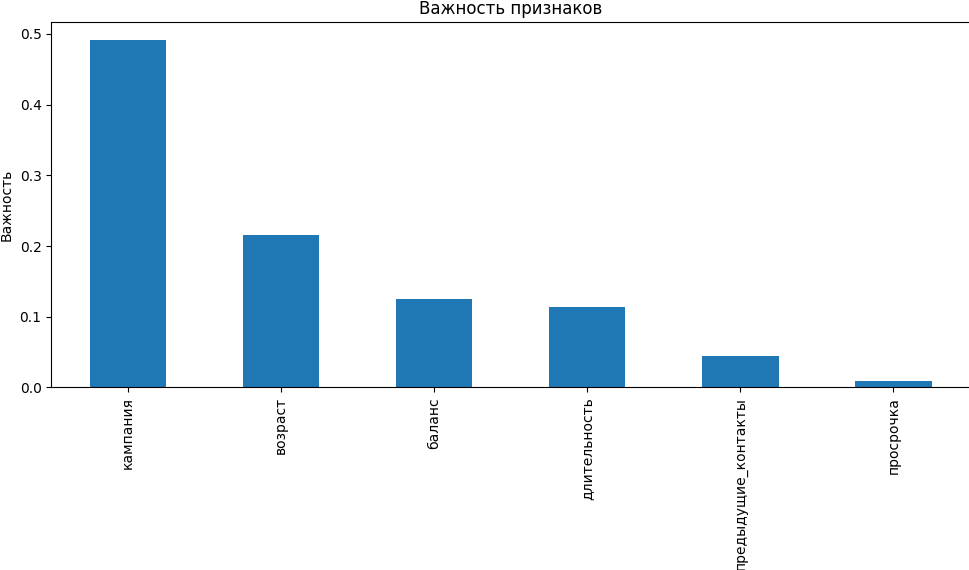
Рассмотрим, как эти признаки повлияли на решения модели:
1️⃣ Кампания
Это число контактов с клиентом во время текущей маркетинговой кампании. Высокая важность говорит о том, что частота контактов сильно влияет на результат — например, если клиенту звонили слишком часто, он, скорее всего, откажется от предложения.
2️⃣ Возраст
Важность этого признака означает, что разные возрастные группы по-разному реагируют на предложение. Например, молодежь менее охотно соглашается на банковские услуги, чем люди среднего возраста.
3️⃣ Баланс
Это сумма средств на счете клиента. Kлиенты с более высоким балансом с большей вероятностью соглашаются на предложение, так как имеют финансовую стабильность и без проблем могут перевести часть средств на срочный депозит.
4️⃣ Длительность
Это продолжительность последнего звонка (в секундах). Клиенты, разговор с которыми длился дольше, очевидно, более заинтересованы.
5️⃣ Предыдущие контакты
Это количество контактов с этим клиентом в предыдущих кампаниях. Низкая важность говорит о том, что прошлый опыт общения не сильно влияет на текущий ответ.
6️⃣ Просрочка
Этот признак показывает наличие просроченного кредита у клиента. Он имеет наименьшую важность, и это означает, что наличие просрочек почти не связано с вероятностью согласия.
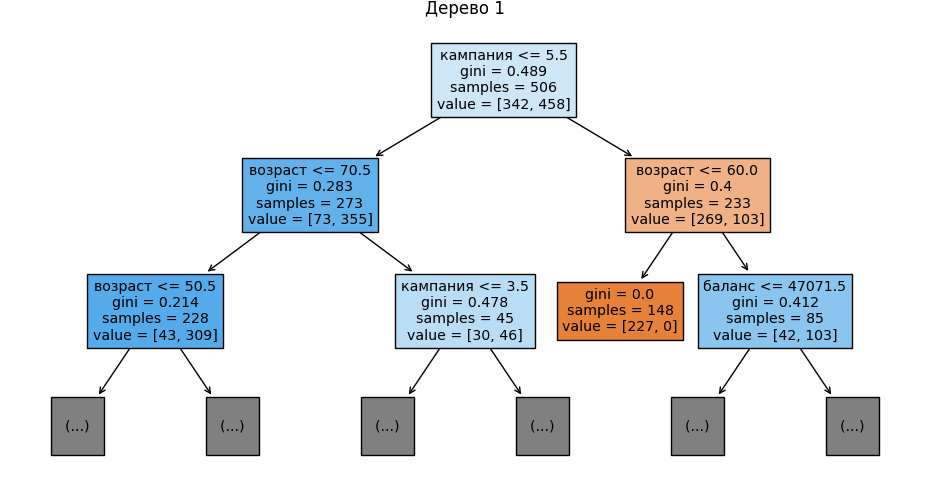
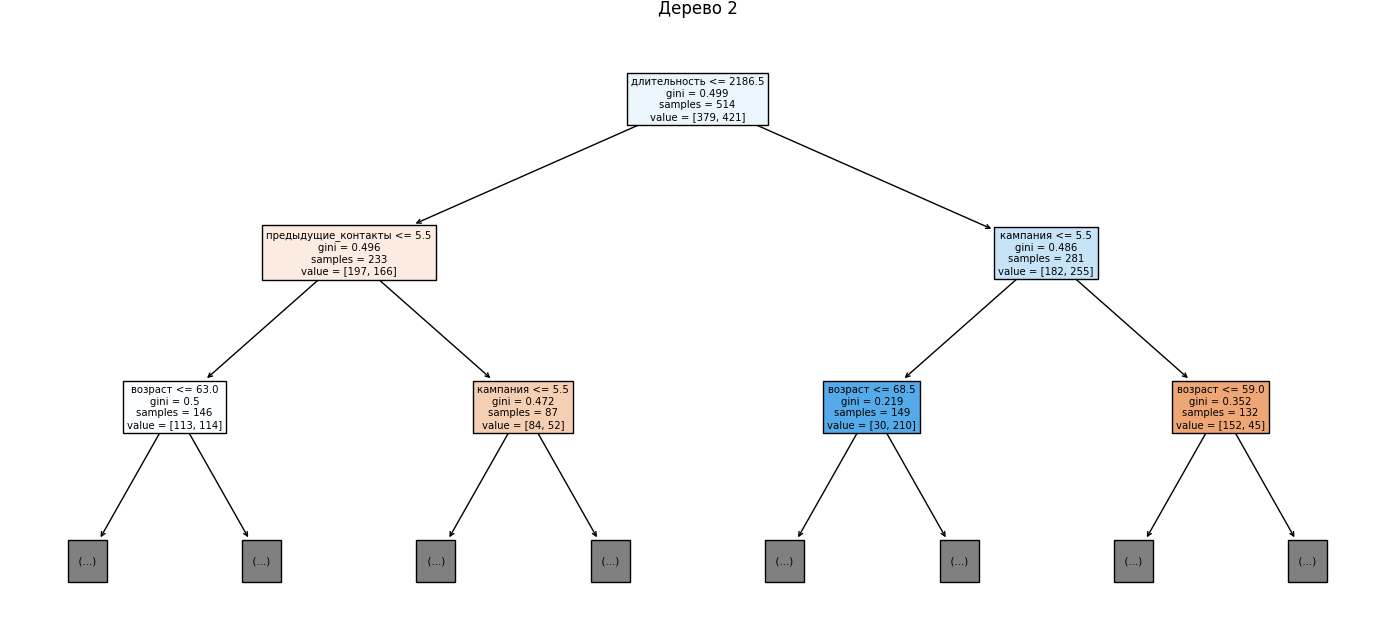
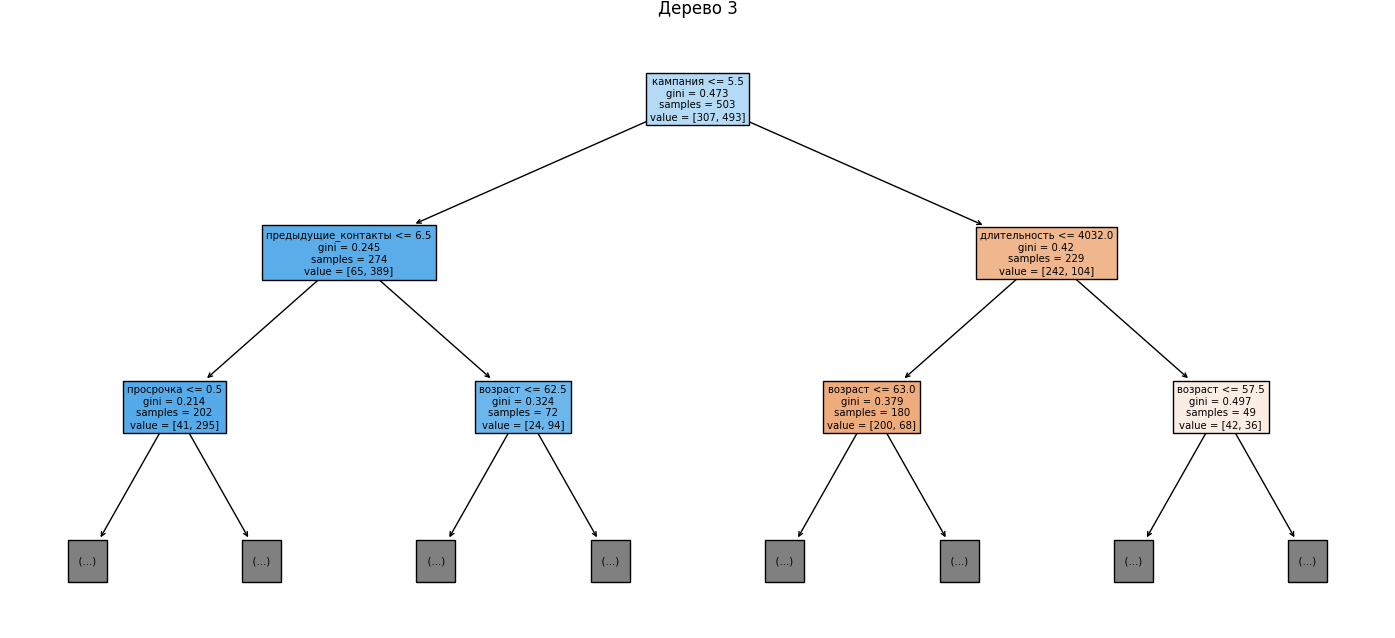
🌳 Шаг 11: Визуализируем первые 3 дерева
Для наглядности отображаем первые три дерева из случайного леса, ограничив глубину двумя уровнями. Это позволяет увидеть, по каким признакам идет деление на первых этапах:
for i in range(3):
plt.figure(figsize=(16, 6))
plot_tree(
best_rf.estimators_[i],
feature_names=X.columns,
filled=True,
max_depth=2
)
plt.title(f"Дерево {i + 1}")
plt.show()
Готовый код:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.tree import plot_tree
from scipy.stats import randint
bank_data = pd.read_csv("bank_data.csv")
X = bank_data.drop("целевой_ответ", axis=1)
y = bank_data["целевой_ответ"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Определение пространства поиска гиперпараметров
param_dist = {
"n_estimators": randint(50, 500),
"max_depth": randint(1, 20)
}
# Создание модели
rf = RandomForestClassifier(random_state=42)
# Поиск лучших гиперпараметров
rand_search = RandomizedSearchCV(
rf,
param_distributions=param_dist,
n_iter=5,
cv=5,
random_state=42,
n_jobs=-1
)
# Обучение RandomizedSearchCV
rand_search.fit(X_train, y_train)
# Лучшая модель
best_rf = rand_search.best_estimator_
print(f"Лучшие гиперпараметры: {rand_search.best_params_}")
# Оценка модели
y_pred = best_rf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average="binary")
recall = recall_score(y_test, y_pred, average="binary")
print(f"Общая точность, Accuracy: {accuracy:.3f}")
print(f"Точность положительного класса, Precision: {precision:.3f}")
print(f"Полнота (Recall): {recall:.3f}")
# Визуализация матрицы ошибок
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm)
disp.plot(cmap="Blues")
plt.title("Матрица ошибок")
plt.show()
# Визуализация важности признаков
feature_importances = pd.Series(best_rf.feature_importances_, index=X_train.columns).sort_values(ascending=False)
plt.figure(figsize=(10, 6))
feature_importances.plot.bar()
plt.title("Важность признаков")
plt.ylabel("Важность")
plt.tight_layout()
plt.show()
# Визуализация первых трех деревьев
for i in range(3):
plt.figure(figsize=(16, 6))
plot_tree(best_rf.estimators_[i], feature_names=X.columns, filled=True, max_depth=2)
plt.title(f"Дерево {i + 1}")
plt.show()
Насколько хорошо работает наша модель
Теперь разберем ключевые метрики и их значение:
- Общая точность Accuracy: 0.88 означает, что модель правильно классифицирует 88% всех случаев.
- Точность положительного класса Precision: 0.867 показывает, сколько из предсказанных положительных случаев (клиентов, согласившихся на услугу) действительно являются положительными. При этом около 13% предсказанных согласившихся на самом деле отказались. Чтобы менеджеры не тратили время на людей, которые не согласятся на открытие срочного вклада, можно поднять порог предсказания, — это уменьшит ложные срабатывания. Еще можно добавить новые признаки, чтобы улучшить классификацию.
- Полнота Recall: 0.951 показывает, что модель почти не пропускает тех, кто действительно согласится на услугу.
- Баланс между Precision и Recall. Precision = 86,7% и Recall = 95,1% говорят о том, что модель почти не пропускает потенциальных клиентов, но иногда ошибается и предсказывает согласие там, где его нет. Это неплохой баланс, так как лучше позвонить лишнему клиенту, чем пропустить заинтересованного.
Подведем итоги
Понимание связи между дисперсией и качеством моделей машинного обучения — необходимый навык для каждого специалиста в области Data Science, позволяющий создавать более эффективные и надежные решения для анализа данных и прогнозирования. Созданная нами модель наглядно демонстрирует, как можно достичь высокой точности в сочетании с устойчивостью к шуму: благодаря механизмам случайного выбора обучающих примеров и признаков, Random Forest успешно снижает дисперсию и создает надежные модели, способные хорошо обобщать закономерности в новых данных.
Математика для дата-сайентистов: разбираемся без лишней воды
Proglib Academy Преподаватели ВМК МГУ собрали все, что реально нужно знать по математике в Data Science — никакой лишней теории, только то, что спрашивают на собеседованиях и используют в работе.
Что внутри:
- Матан — разберемся, зачем он вообще нужен в машинном обучении
- Линейная алгебра — перестанете бояться матриц и научитесь ими пользоваться
- Комбинаторика — считаем сложные штуки просто
- Теорвер и статистика — без этого в данных как без рук
- Машинное обучение на практике — применяем все изученное
Почему стоит попробовать:
- Те же задачи, что дают на входе в ШАД Яндекса
- Научитесь не тупить перед большими датасетами
- Поймете, как работают алгоритмы, а не просто будете их вызывать
- Можно задавать вопросы людям, которые реально в теме





Комментарии