Условие задачи о беглеце
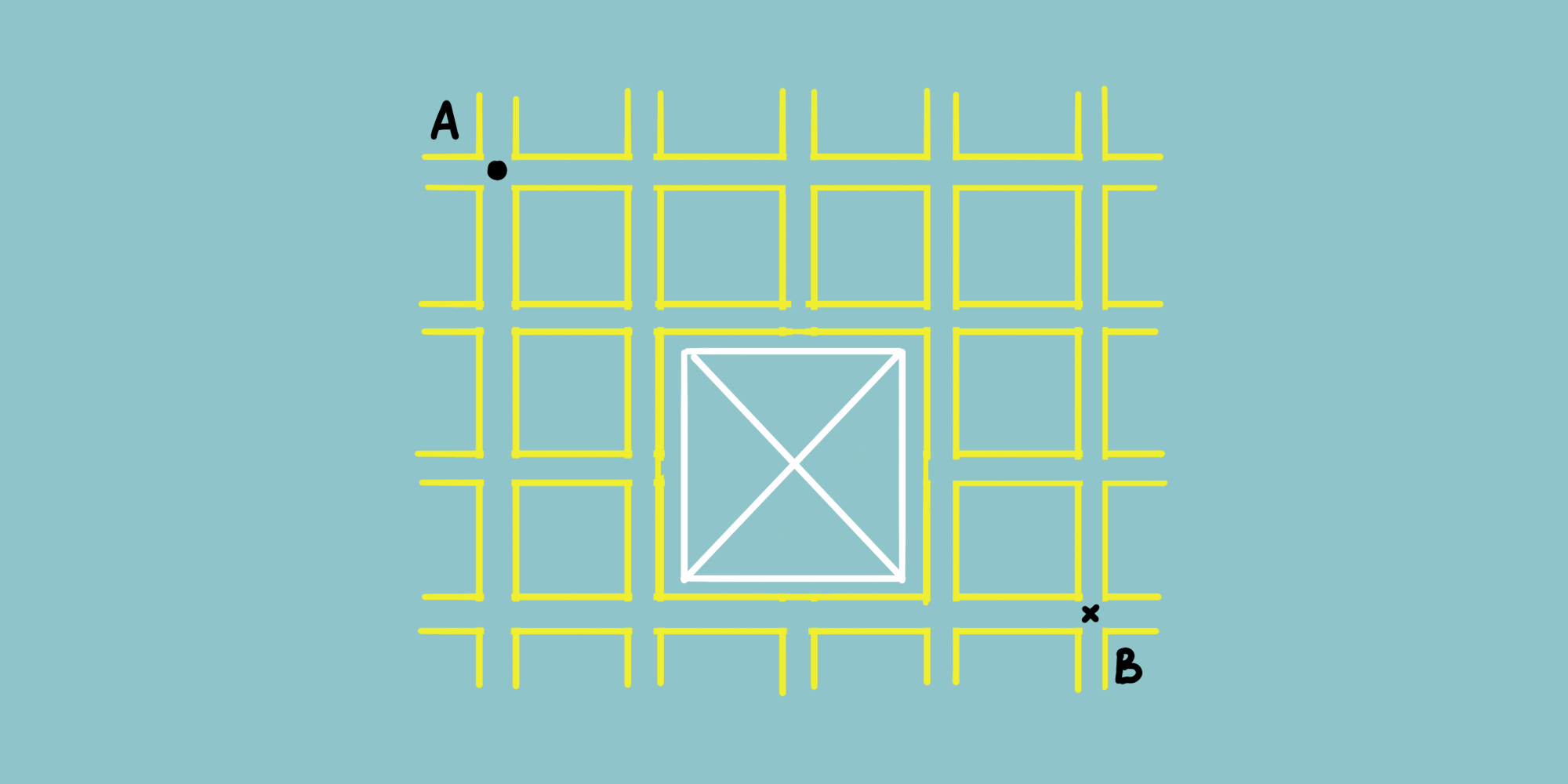
На рисунке приведён план одного из этажей тюрьмы. Найдите число различных кратчайших путей, которыми беглец может добраться по системе коридоров из точки A в точку B.
Решение – в следущей задаче.
Эта задача – десятый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую головоломку о шести шахматных конях.
Решение задачи о шести шахматных конях
Предварительное замечание: под «перемещением фигуры в соответствии с шахматными правилами» понимался исключительно способ движения фигуры коня и то, что две фигуры не могут встать на одно поле. Но не последовательное чередование ходов белых и чёрных. К счастью, большинство ответов читателей были приведены именно в таком предположении. Но, конечно, вы можете предложить своё решение с учётом дополнительных ограничений – так ещё интереснее.
Ответ: Минимальное количество ходов, необходимое для решения головоломки (с учётом указанной оговорки), составляет 16.
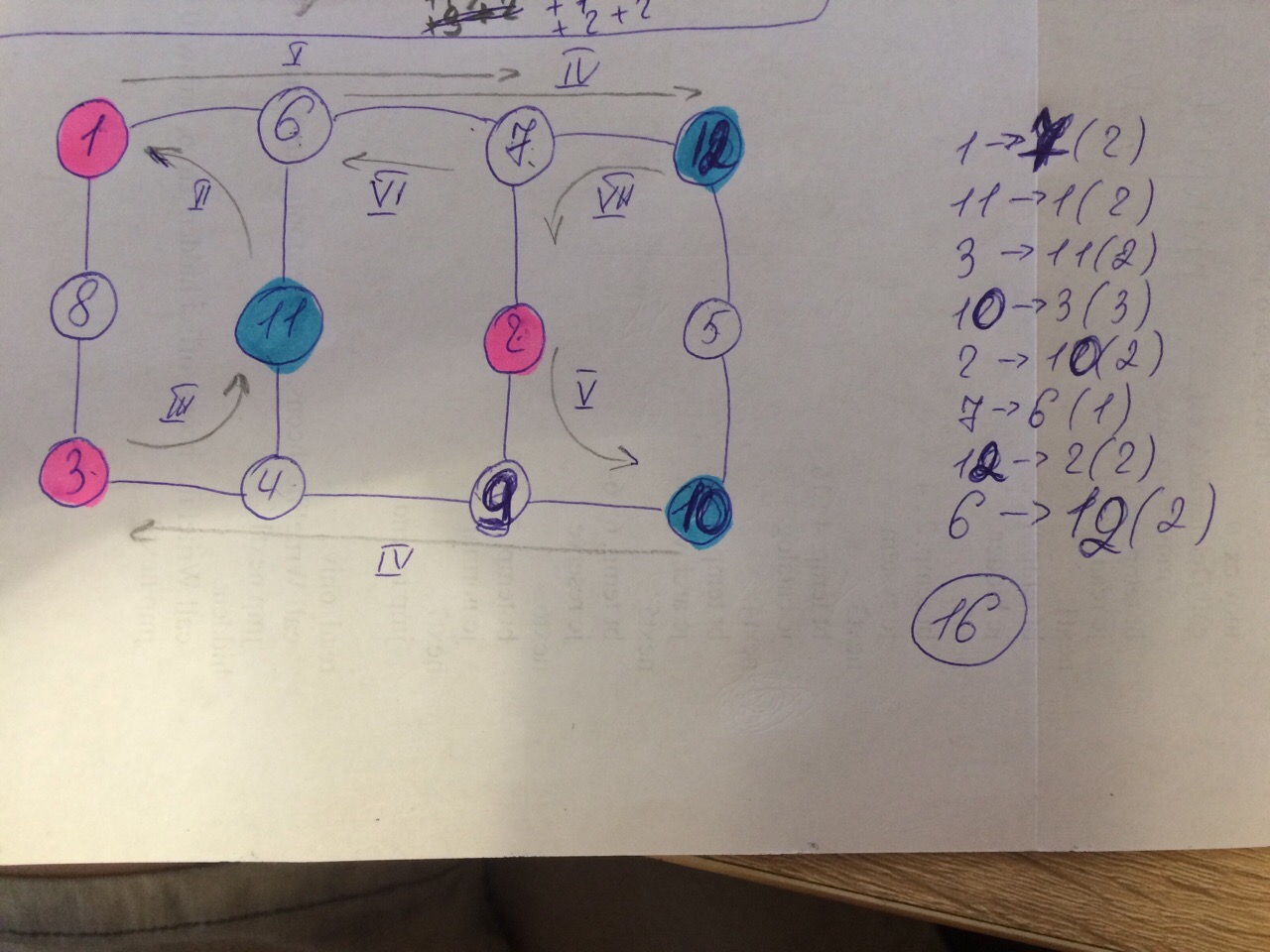
Решение. Начальное состояние удобно представить в виде графа, как на рисунке ниже. Цвет добавлен, чтобы было проще понять связи между полями. Линии соединяют те позиции, между которыми может двигаться фигура коня.
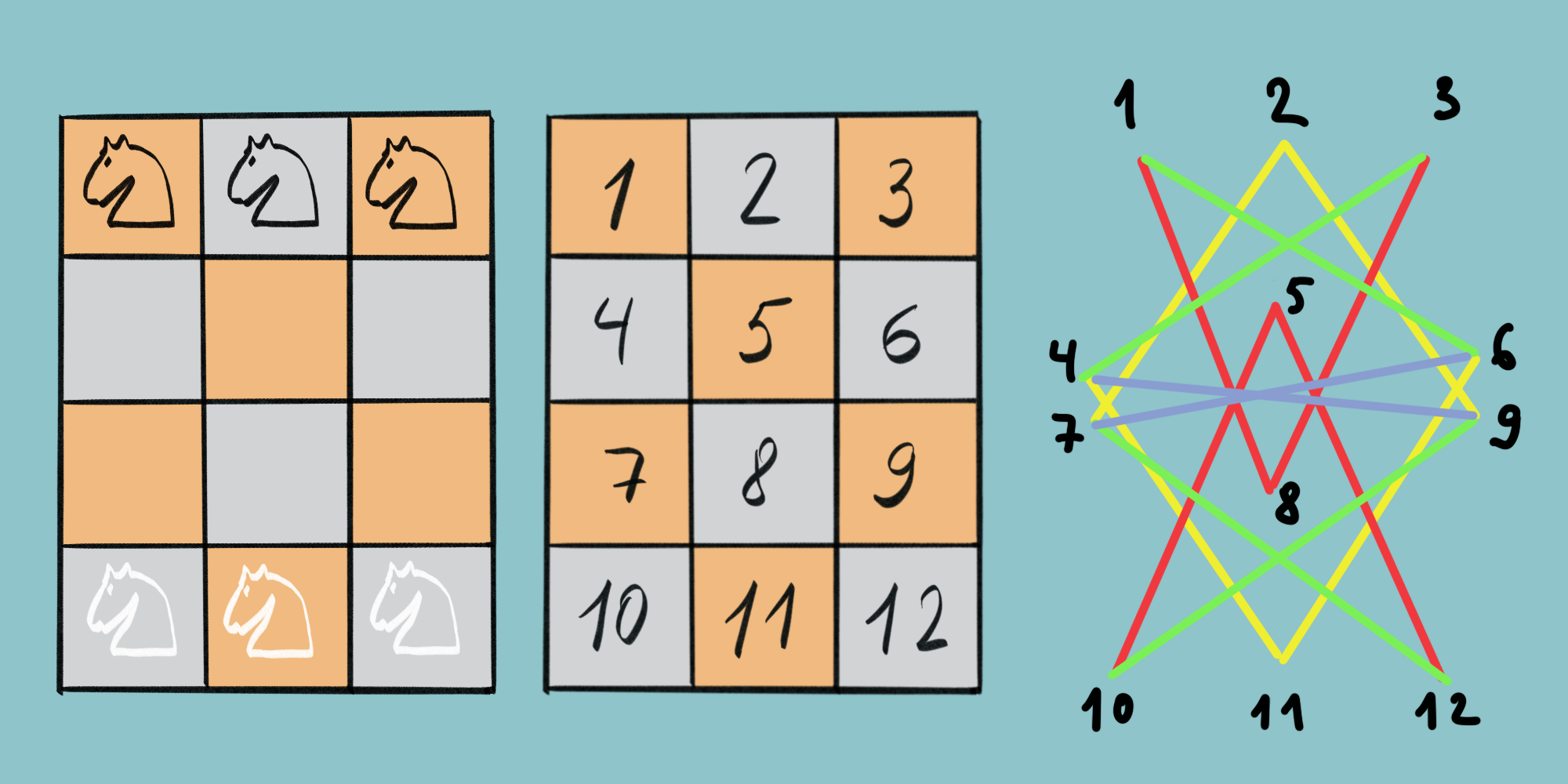
Приведённый граф далее можно распутать, как показано на следующем рисунке.
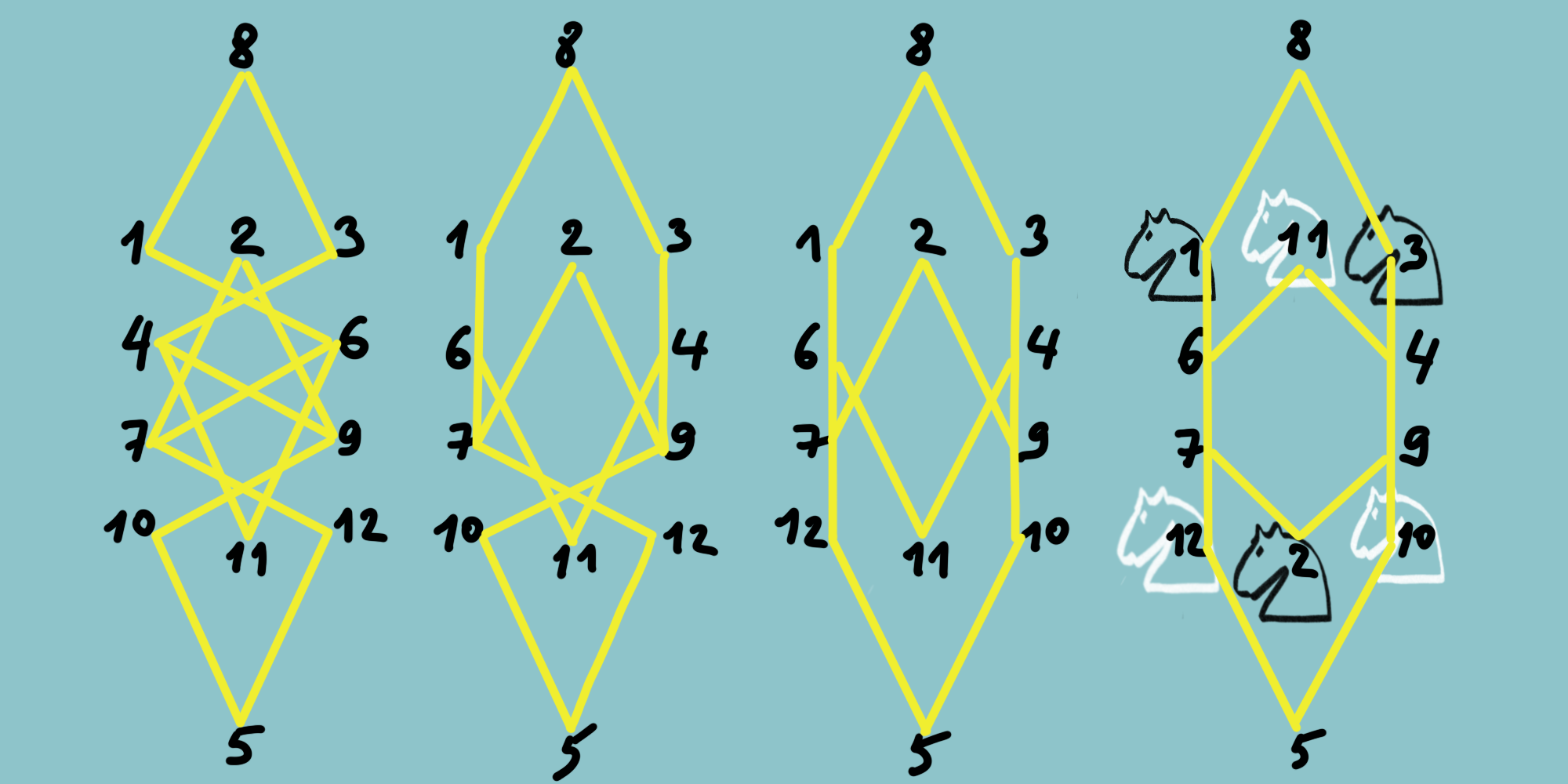
Распутываем граф. Узлы 8 и 5 в сравнении с исходной картинкой мы переместили соответственно вверх и вниз. Узлы 4 и 6 поменяли местами, чтобы получить второй рисунок. Затем обменяли узлы 10 и 12, получили третье представление. Наконец, то же сделали с узлами 11 и 2. Показали где исходно находятся белые и чёрные фигуры. Теперь у нас есть развёрнутое представление графа.
Ходы чёрных. Чтобы достичь цели головоломки, один из двух чёрных коней в начальных позициях 1 или 3 должен переместиться в 12 или 10. Пусть конь в позиции 1 перемещается в 12, что ближе к его исходной позиции, чем позиция 10. По кратчайшему пути потребуется 3 хода (1 – 6 – 7 – 12). Другим двум чёрным коням понадобятся в сумме как минимум 4 хода, чтобы добраться от позиций 2 и 3 к позициям 10 и 11 (например, 2 – 9 – 10 и 3 – 4 – 11).
А белые кони? Симметрия подразумевает одинаковую нижнюю границу из 7 ходов для белых коней. Таким образом, головоломка не может быть решена менее чем за 14 ходов. Но задачу нельзя решить ни за 14, ни за 15 ходов. Это связано с блокировками фигур противоположного цвета и можно доказать от противного.
Доказательство. Для удобства далее будем обозначать чёрных коней – Ч, белых коней – Б. Предположим, что существует последовательность ходов, которая решает головоломку менее, чем за 16 ходов. В такой последовательности Ч1 должен будет достичь поля 12 за 3 хода, потому что он не может сделать это за 4 хода. А если сделает за 5 или более ходов, общее их количество будет уже не менее (5 + 4) + 7 = 16.
Но прежде чем Ч1 сможет перейти с 6 на 7, должны произойти ходы
- Б(12 – 7 – 2), этому должно предшествовать
- Ч(2 – 9), этому предшествует
- Б(10 – 9 –4), этому предшествует
- Ч(3 – 4 – 11), этому предшествует
- Б(11 – 6).
Но такой ход блокирует Ч1, и таким образом, необходимое количество ходов превышает 15.
Но головоломка может быть решена за 16 ходов, например, в следующей последовательности:
- Ч(1 − 6 − 7)
- Б(11 − 6 − 1)
- Ч(3 − 4 − 11)
- Б(10 − 9 − 4 − 3)
- Ч(2 − 9 − 10)
- Ч(7 − 6)
- Б(12 − 7 − 2)
- Ч(6 − 7 − 12)
Соответствующее решение мы изобразили на рисунке.
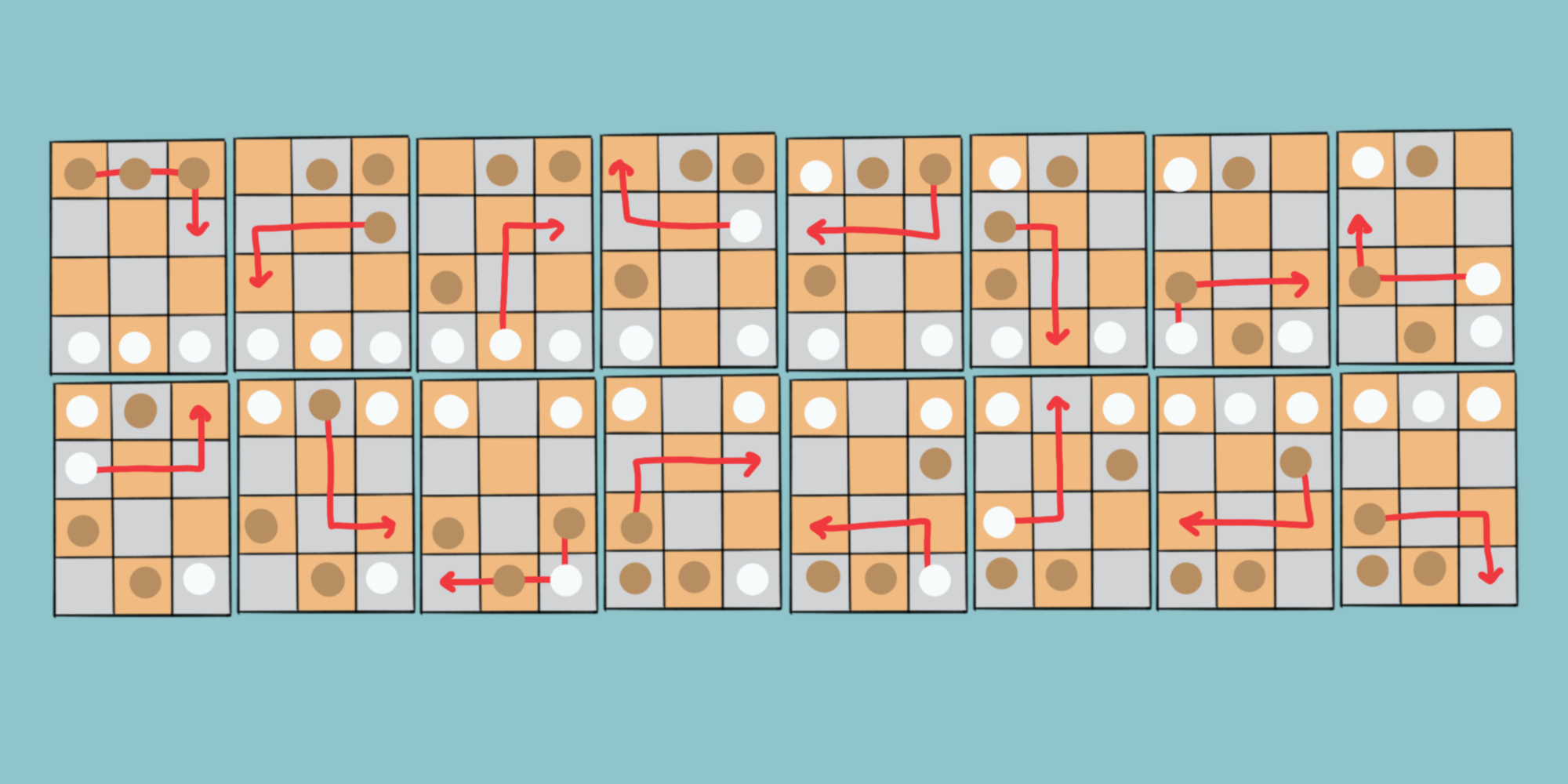
Как ответили читатели Библиотеки программиста? В первую очередь мы рассматриваем ответы на сайте. Читатель Sansss предложил решение (с учётом указанной выше оговорки) за 18 ходов, то есть чуть больше, чем получилось у нас:
За 18 ходов точно можно переместить фигуры. 12 – 7 7 – 6 1 – 8 6 – 1 2 – 7 7 – 12 10 – 9 9 – 2 3 – 4 4 – 9 9 – 10 8 – 3 3 – 4 4 – 9 11 – 4 4 – 3 9 – 4 4 – 11

Читатель Bodya.Net привёл решение с учётом более жёсткого ограничения на чередование ходов чёрных и белых. Распутанный граф вышел таким же, как у нас. Получилось 22 хода, правда не описана строгая последовательность движения чёрных и белых по отдельности.
Начертил граф, если соблюдать правила (чередовать ходы черных и белых), получается, что каждому стороне нужно 11 шагов. Т.е. 22 хода. Я просто по этому графу веду черные фигуры по верху, а белые по низу. 1 – 8 – 3 – 4 – 11 2 – 9 – 10 – 5 – 12 3 – 4 – 9 – 10 10 – 5 – 7 – 2 11 – 6 – 1- 8 – 3 12 – 7 – 6 – 1 Наверное есть более короткие пути, но я их не нашел.
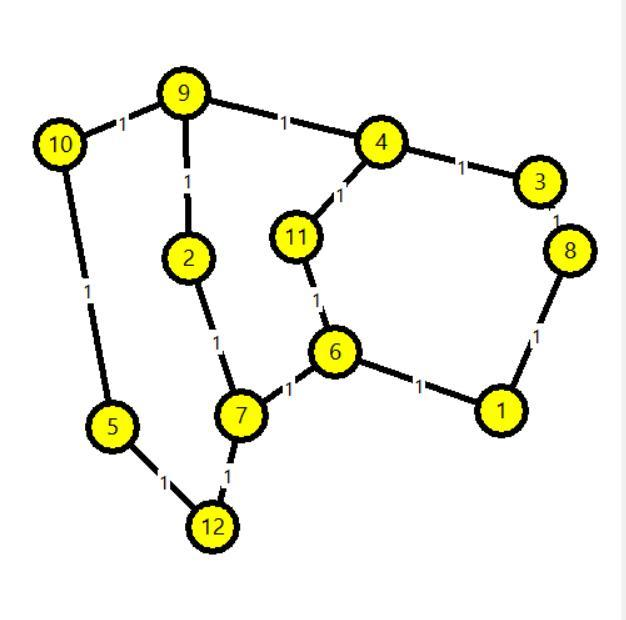
Для случая чередующихся ходов другие участники обсуждения в сообществе вк также указали 22 хода. Там же первым нашёл такой же путь, как мы, читатель Дима Алексеев:
16 ходов, стрелками с римскими цифрами обозначены направление и номер хода, справа от рисунка последовательность ходов, в скобках указано кол-во шагов
А Дмитрий Шелухин привёл доказательство о минимальном количестве ходов:
«Можно даже доказать, что 16 это минимальное количество ходов (Min):
1. Min>=14, это уже известно
2. Min !=14. С учетом симметрии, есть 2 разных потенциальных способа за 14 ходов решить задачу: когда центры идут в противоположные углы (1, 12) или когда они идут в углы с одной стороны (1, 10). В первом случае сразу находится блокировка (на пути 1-6-11), во втором получается циклическая зависимость (прежде чем сдвинуть коня из 11 нужно ... убрать коня из 11), т.е. тоже кони блокируют друг друга
3. Для того, чтобы переставить 3 коней с одной стороны на другую требуется всегда нечетное число ходов. Какой бы ни оказалась перестановка ((1, 2, 3) -> (12, 11, 10), например) сумма минимальных расстояний всегда будет нечетной. Т.к. в графе только четные циклы, то даже если расстояния будут неминимальными, их четность не изменится. Раз надо переставить 6 коней, то ответ всегда будет четным».


Комментарии