Условие задачи
Исчезая, Чеширский кот пообещал Алисе вернуться при выполнении одного условия 😼 . Нужно произнести палиндром WAS IT A CAT I SAW (англ. «Не кота ли я видела?») столько раз, сколькими способами тот может быть прочитан внутри ромба, изображённого на картинке. Это если Алиса думать не хочет. Или назвать само число, но только одно.
Начинать можно с любой буквы W и двигаться через соседние символы вверх, вниз, влево или вправо. Одну и ту же букву можно использовать в последовательности несколько раз.
Алиса просит вас помочь: какое число назвать?
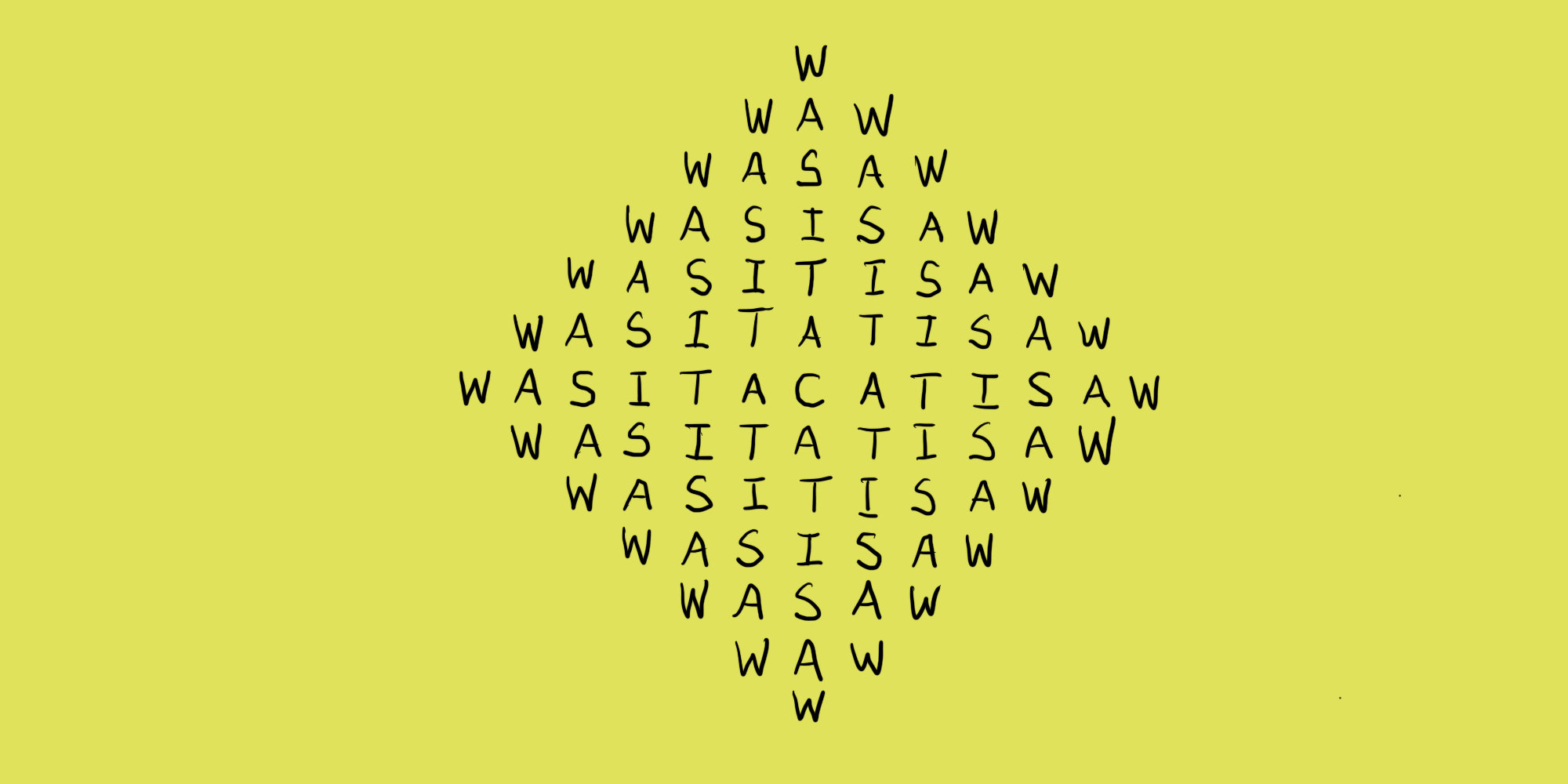
Решение – в следущей задаче.
Эта задача – одиннадцатый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую головоломку о беглеце.
Решение задачи о беглеце
Чтобы решить эту задачу, проще всего использовать метод динамического программирования. Недавно мы рассказывали о похожем, но более сложном классе задачи о рюкзаке.
Ответ: 17.
Решение: Подход заключается в том, чтобы найти количество кратчайших путей из А до каждого узла сетки, образованной коридорами, как на рисунке ниже. Начиная с присвоения 1 точке A числа в узлах могут быть найдены вычислением построчно и слева направо в каждой строке. Если перекресток имеет и левого, и верхнего соседа, число определяется как сумма их чисел; если пересечение имеет лишь один такой соседний узел, число приравнивается числу соседа.

Как ответили читатели Библиотеки программиста? Другое решение, основанное на комбинаторном подходе, привёл пользователь s.pro1990 :
Вначале рассмотрим ситуацию без запретной зоны. Получится сетка 4 на 5, по которой кратчайших путей будет 7!÷(3!4!)=35. В самом деле, каждый раз можно пройти вниз до следующей точки, либо вправо, в сумме мы должны пройти вниз 3 раза и вправо 4 раза. Количество вариантов это число сочетаний из 7 по 3, ну или из 7 по 4, в данном случае не важно. В запретную зону два входа, и два выхода из неё, и ими мы не можем воспользоваться. До каждого из входов 3 варианта пути, суммарно запретная зона перекрывает нам 3×2×2=12 путей [...] Да, ещё я не учёл, что от одного из выходов 2 варианта попасть в точку В. Итого теряется 3×2×2 путей через этот выход, плюс 3×2 через другой, суммарно 18. Остаётся 35-18=17.


Комментарии