Условие задачи о шести шахматных конях
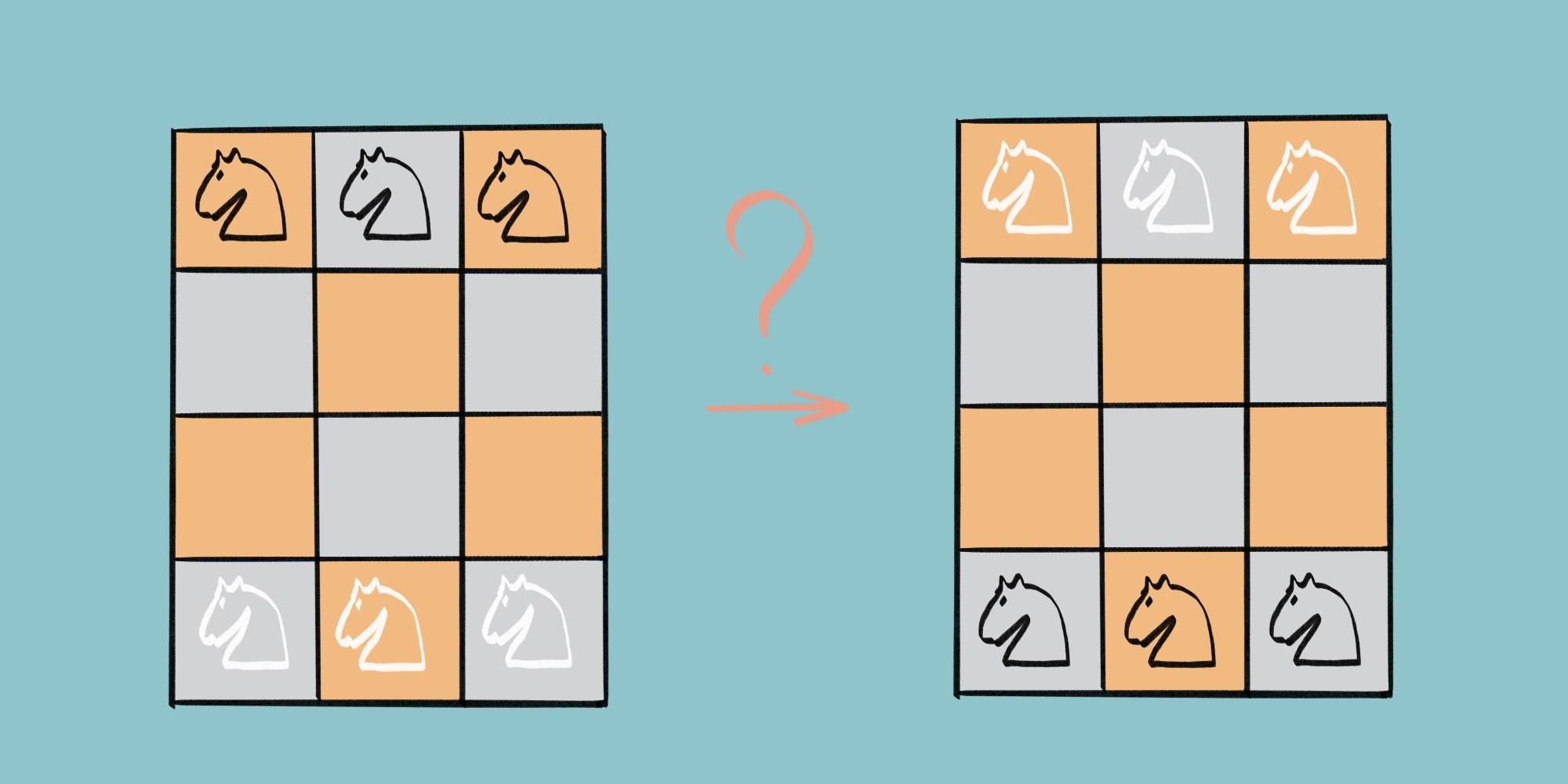
На шахматной доске 3 × 4 находится шесть фигур: три белых коня в нижнем ряду, и три чёрных коня в верхнем. Предложите алгоритм, при котором чёрные и белые фигуры обменяются положениями, как показано на рисунке, за минимальное количество ходов. Один ход соответствует одному перемещению фигуры в соответствии с шахматными правилами.
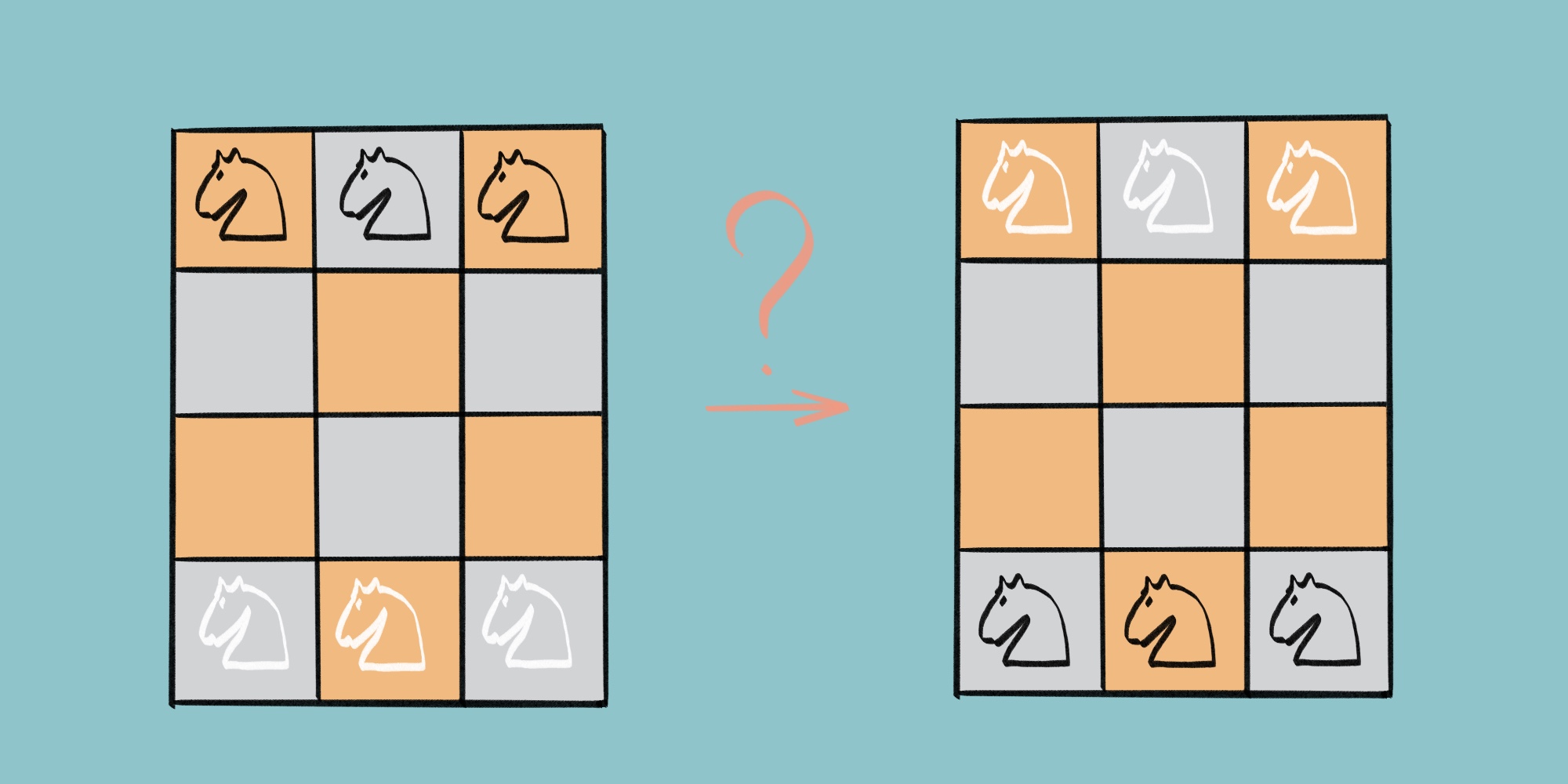
Для описания алгоритма используйте нумерацию полей как на рисунке ниже.
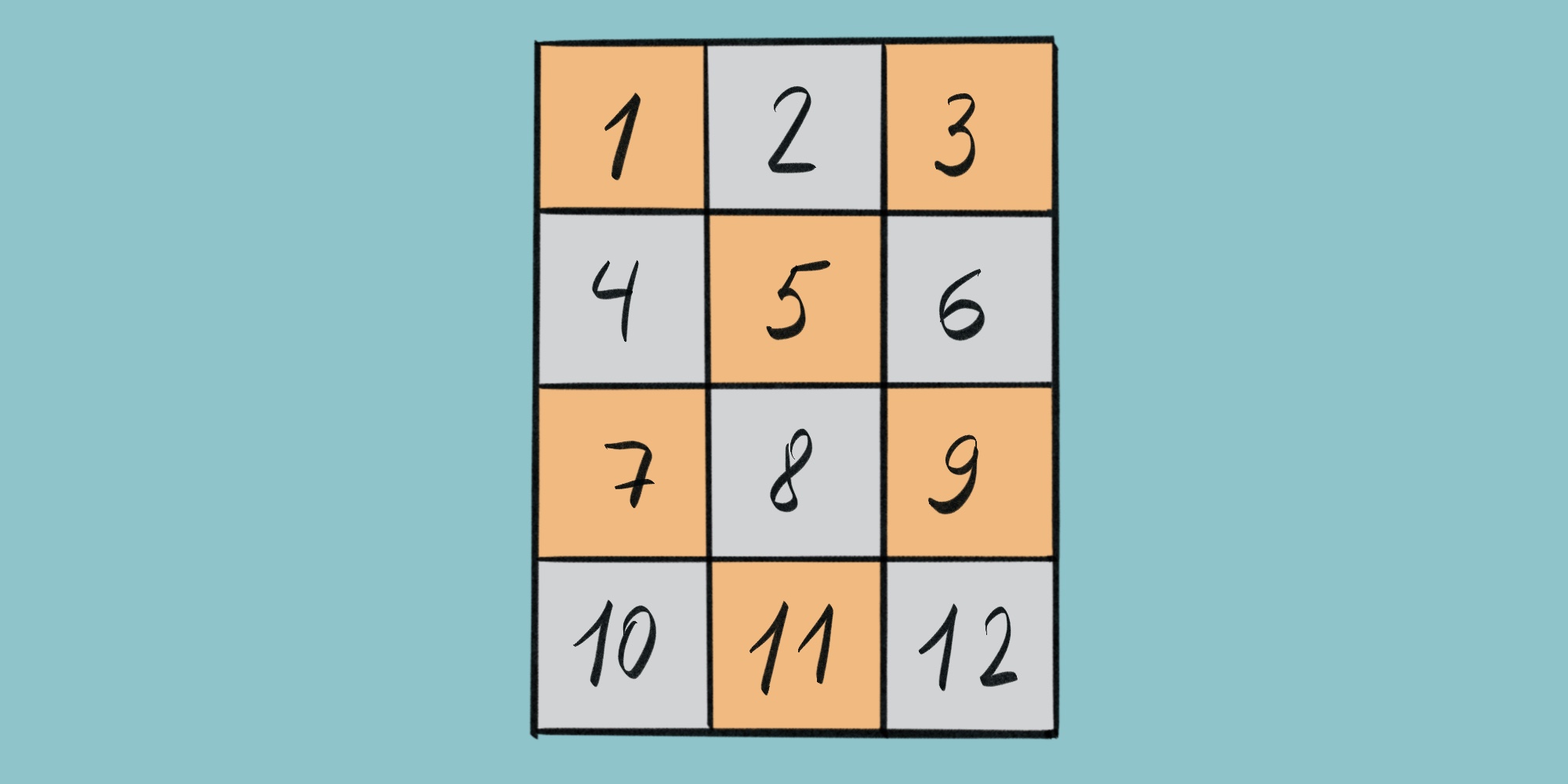
Решение – в следущей задаче.
Эта задача – девятый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую головоломку о вирусе в колонии бактерий.
Решение задачи о вирусе в колонии бактерий
Ответ: нет, колония обречена.
Решение. Легко проверить, что количество бактерий и вирусов будет меняться со временем по следующему закону:
| Время (минуты) | Кол-во вирусов | Кол-во бактерий |
| 0 | 1 | N |
| 1 | 2 | 2(N-1) |
| 2 | 22 | 2(2N-2-2) = 22(N-2) |
| 3 | 23 | 2(4N-8-4) = 23(N-3) |
| 4 | 24 | 24(N-4) |
| ... | ... | ... |
| t | 2t | 2t(N-t) |
Отсюда ясно, что при t = N количество бактерий обратится в ноль.
Как ответили читатели Библиотеки программиста? Первым правильный ответ на сайте, что колония бактерий не выживет, дал muradoz. Само решение тоже верное, но шло от конечной точки, и поэтому получилось немного более запутанным:
К моменту T бактерий было бы N*2^T без вирусов. Сколько из этого убили вирусы? За первую минуту была убита 1 бактерия, которая превратилась бы в 2^T. За вторую минуту 2 вируса убили 2 бактерии, которые бы стали к моменту времени Т числом 2^(T-1). То есть вирусы убили от потенциального числа к моменту Т сумму по к от 1 до T следующей штуки: число вирусов в момент к (то есть 2^k) на 2^(T-k). Эта сумма T*2^T. Колония проживет N минут.



Комментарии