🐍🤔 «Задумчивый» код: временная сложность операций со структурами данных в Python

Временная сложность алгоритма – это показатель, который описывает, как растет время выполнения алгоритма при увеличении количества входных данных. Знание временных сложностей помогает оценить, насколько хорошо будет работать алгоритм на больших объемах данных, и выбрать наиболее эффективный подход для решения задачи.

Представим, что у нас есть список из 10 элементов, и мы хотим найти определенный элемент в этом списке. Мы можем просто пройтись по списку с начала до конца и посмотреть, есть ли там нужный элемент. Для списка из 10 элементов это займет относительно немного времени.

Но что если список состоит из 100 элементов? Или из 1000? 1000000? Алгоритм, при котором мы просматриваем весь список, будет работать все медленнее и медленнее по мере роста размера списка. Временная сложность позволяет нам описать, насколько замедлится алгоритм при увеличении входных данных. Для нашего примера с поиском в списке временная сложность будет O(n), где n – размер списка. Это означает, что время выполнения алгоритма растет пропорционально размеру входных данных.

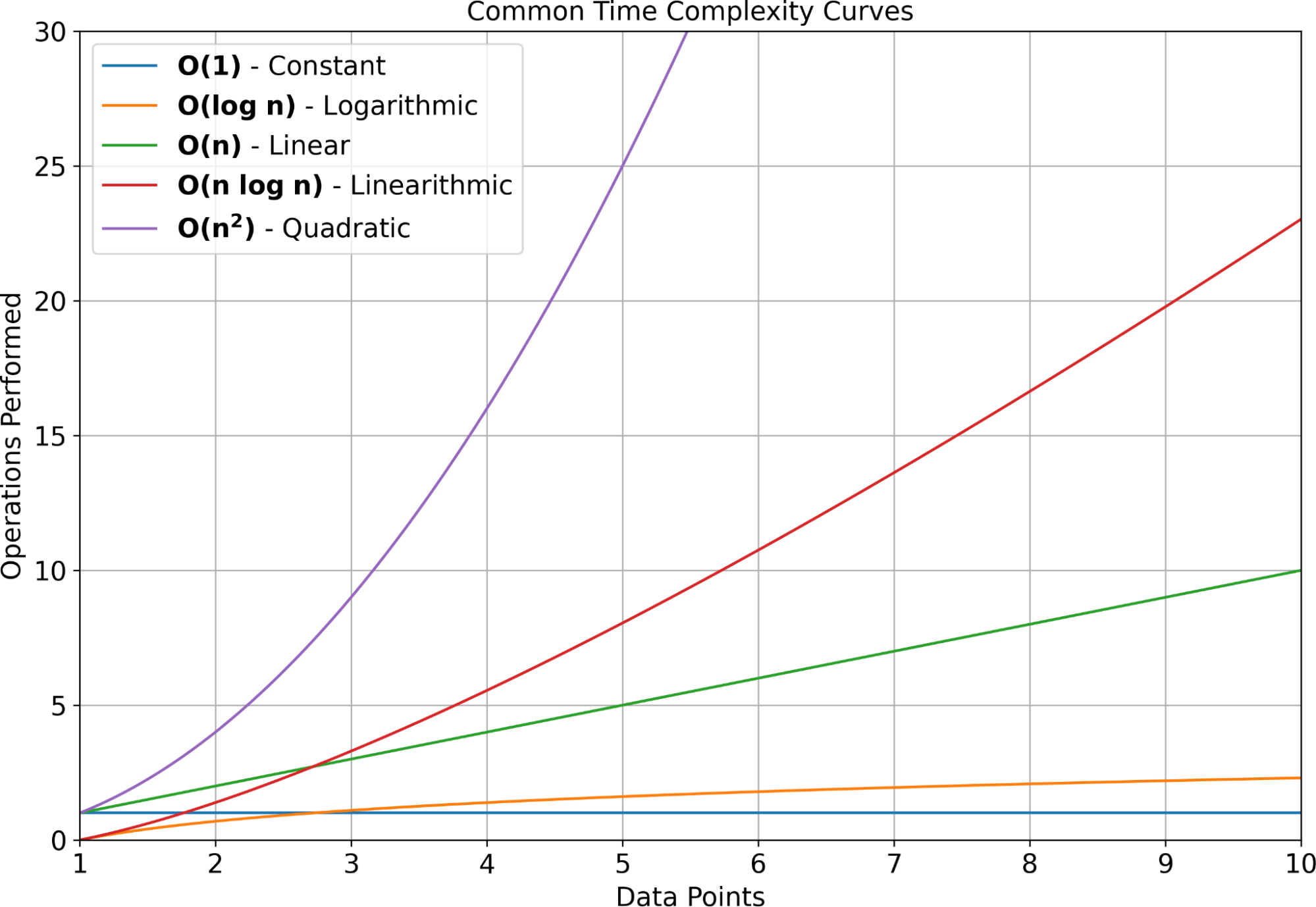
Вот основные виды временных сложностей:

1. O(1) – константное время. Время выполнения операции не зависит от объема входных данных. Пример: len(list) – получение длины списка выполняется за константное время, независимо от размера списка.
2. O(n) – линейное время. Время выполнения пропорционально размеру входных данных. Пример: поиск элемента в списке с помощью оператора in (item in some_list) требует линейного просмотра списка.
3. O(n^2) – квадратичное время. Очень неэффективные алгоритмы, где время растет квадратично относительно входных данных. Пример: вложенные циклы для обработки всех пар элементов в списке.
4. O(n log n) – логарифмическое время. Более эффективные алгоритмы, чем O(n^2), но медленнее, чем O(n). Пример: алгоритм сортировки sorted(list).
5. O(log n) – линейно-логарифмическое время. Очень эффективные алгоритмы, время работы которых растет логарифмически от размера входных данных. Пример: двоичный поиск в отсортированном списке.

Более медленные сложности: O(n^3), O(n^2 log n), O(2^n) и т.д. встречаются в повседневном программировании гораздо реже.

Трей Ханнер написал подробнейшую статью о временной сложности различных операций со структурами данных Python. Автор отмечает, что операции вставки и удаления в списках имеют разную сложность в зависимости от позиции – в конце списка они выполняются очень быстро, а в начале списка – очень медленно (потому что после операции надо сдвинуть вправо все элементы). Вот несколько примеров временной сложности основных операций из статьи:

Список (List)

• Доступ к элементу по индексу (sequence[index]) – O(1)
• Присваивание элемента по индексу (sequence[index] = value) – O(1)
• Добавление в конец списка (sequence.append(item)) – O(1)
• Удаление с конца списка (sequence.pop()) – O(1)
• Вставка в начало списка (sequence.insert(0, item)) – O(n)
• Удаление из начала списка (sequence.pop(0)) – O(n)
• Проверка на вхождение элемента (item in sequence) – O(n)
• Получение длины списка (len(sequence)) – O(1)

Двусторонняя очередь (Deque)

• Добавление в конец (queue.append(item)) – O(1)
• Удаление с конца (queue.pop()) – O(1)
• Добавление в начало (queue.appendleft(item)) – O(1)
• Удаление с начала (queue.popleft()) – O(1)
• Проверка на вхождение элемента (item in queue) – O(n)

Словарь (Dict)

• Доступ по ключу (mapping[key]) – O(1)
• Присваивание по ключу (mapping[key] = value) – O(1)
• Удаление по ключу (mapping.pop(key)) – O(1)
• Проверка наличия ключа (key in mapping) – O(1)
• Получение значения по ключу (mapping.get(key)) – O(1)
• Итерирование по паре ключ–значение (for k, v in mapping.items()) – O(n)

Множество (Set)

• Добавление элемента (my_set.add(item)) – O(1)
• Удаление элемента (my_set.remove(item)) – O(1)
• Проверка на вхождение элемента (item in my_set) – O(1)
• Итерирование по элементам множества (for item in my_set) – O(n)

Куча (Heap)

• Создание кучи из списка (heapq.heapify(sequence)) – O(n)
• Извлечение минимума (heapq.heappop(sequence)) – O(log n)
• Добавление элемента (heapq.heappush(sequence, item)) – O(log n)
• Бинарный поиск в отсортированном списке (bisect):
• Получение индекса для вставки (bisect.bisect(sorted_seq, item)) – O(log n)
• Вставка с сохранением сортировки (bisect.insort(sorted_seq, item)) – O(n)

На курсе «Алгоритмы и структуры данных» наши опытные преподаватели помогут вам распутать самые сложные алгоритмические узлы и покажут, насколько завораживающим может быть мир алгоритмов.

Программа курса

1. Введение. Производительность алгоритмов
2. Работа с числами
   
3. Массивы
   
4. Алгоритмы на массивах
   
5. Списки. Стек, очередь, дек
   
6. Очередь с приоритетом
   
7. Основы сортировки
   
8. Порядковые статистики
   
9. Деревья
   
10. Хеш-таблицы
    
11. Жадные алгоритмы. Динамическое программирование
    
12. Графы и рекурсия
    
13. Строки
    
14. Криптография
    
15. Длинные числа