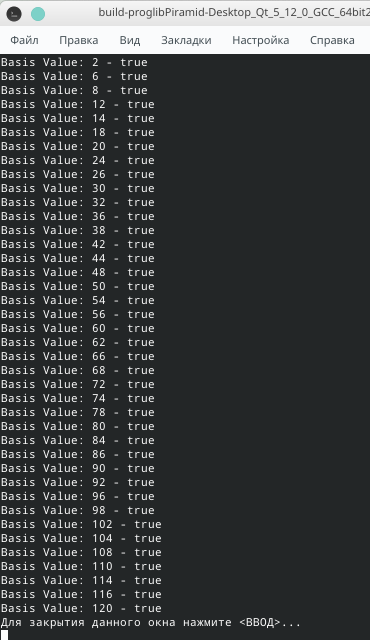
Как вариант N = 2 * k + (3 - (k // 2)). Где // результат деления с отбрасыванием целой части.
Неужели это верно для всех простых N которые соответствуют условию r=n(n+1)/2 mod 3, где остаток r должен быть равен 0? Исключение из правил числа 3 и 5...
Ну думаю решил. Для чётных выслеживается зависимость: r=((N^2)/2+N/2) mod 3 (Можно упростить до r=((N^2 + N)/2) mod 3). Если остаток r равен 0, то N будет верным основанием башни. Для нечетных могу ошибаться, но выслеживается простая зависимость: r=N^2 mod 3, где N=3 исключение.
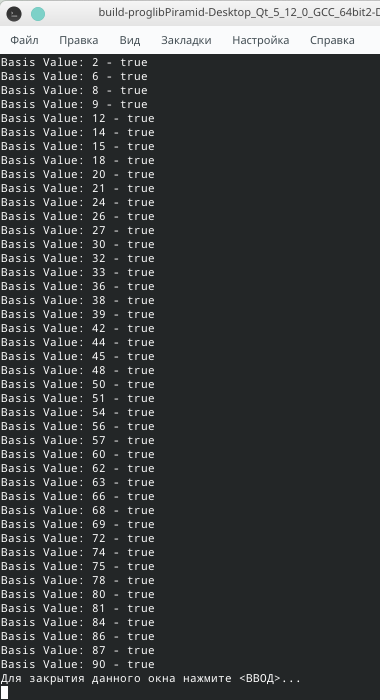
Хорошо, можно тогда уточнить условие? Лестница обязательно должна иметь последнюю верхнюю ступень или нет? Просто не совсем понятно как решение может быть для нечетных чисел...
https://pastebin.com/Qm3Ru08L . Вот, добавил комментарии. Старую ссылку удаляю. Критика приветствуется.
И да, нашел последовательность. count = m*(n+1)+n
Вот так выглядит, чисто вывод. Красивую визуалку не делал, но можно, если нужно.
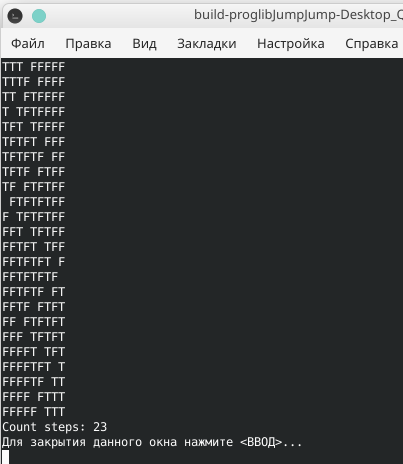
Как и сказал, решение не очень красивое. Решил, скажем, шаблонами. Т.е. При определенной комбинации из 5 символов, где в центре ' '(пробел)(Пример: TF FT или FT TF) определяется какая 'лягушка' и насколько 'прыгает'. Просто изначально ставил цель делать промежуточный вывод, а не просто подсчитать количество. Проще часть исходника кинуть).
Или при m=11 и n=33. Число шагов получается 407