Условие задачи
Вы – расхититель гробниц. Нужно пройти над пропастью по лестнице, охраняемой Сфинксом. Как водится, Сфинкс задает загадку. Решите задачу неверно – и лестница провалится в пропасть, когда вы по ней пойдете.
Условие задачи. Строительными блоками лестницы являются балки с квадратным сечением, соединенные по три таким образом, что срез имеет форму тримино (как у правой фигуры на рисунке). Для каких n можно составить лестницу из таких тройных блоков, если n – число квадратных балок в ее основании? На рисунке приведено поперечное сечение лестницы для n = 8.
Другими словами, какие лестничнообразные фигуры с основанием из n квадратов можно разрезать нацело на тримино?
Решение – в следущей задаче.
Эта задача – пятнадцатый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую – алгоритмическую задачу о прыгающих лягушках. Ответ и новая задача будут опубликованы в 14:00 в субботу.
Решение алгоритмической задачи о лягушках
Если вы не решали эту задачу, прежде чем читать приведенный ниже текст, прочитайте условие и попробуйте решить самостоятельно!
Решение. Движение лягушки сводится либо к прыжку через лягушку противоположного вида, либо к переходу лягушки на соседнюю пустую клетку. Таким образом, если мы найдем общее количество прыжков и переходов, мы узнаем общее количество ходов.
Прыжок – единственный способ, которым лягушки противоположного вида могут преодолеть друг друга. Мы сталкивались с этим ранее в предыдущих задачах: получается, что для того, чтобы преодолеть друг друга, им необходимо совершить n2 прыжков в случае n настоящих и n виртуальных лягушек.
Сдвиг. Рассмотрим далее ситуацию для лягушек одного вида. Мы знаем, что они не могут перепрыгивать друг через друга. Первая лягушка переместится на n + 1 клеток и окажется в ячейке n + 2, вторая лягушка передвинется на n + 1 клеток до ячейки n + 3, и т. д. Чтобы оказаться в нужной позиции, вместе все лягушки одного вида должны переместиться на n (n + 1) клеток. Аналогично должны сделать их виртуальные аналоги. То есть все эти реальные и виртуальные земноводные переместятся на 2 n (n + 1) клеток. Поскольку один прыжок охватывает две ячейки, и их n2, количество сдвигов должно составить 2n (n + 1) – 2n2 = 2n.
Алгоритм. Существует два симметричных алгоритма для решения головоломки: один начинается со сдвига крайней к пустой ячейки настоящей лягушки, другой – со сдвига виртуальной. Опишем первый. Алгоритм может быть получен методом грубой силы: его ходы определены однозначно, потому что альтернативные ходы приводят к очевидным тупиковым ситуациям. В частности, когда есть выбор между сдвигом и прыжком, должен быть сделан прыжок.
Ниже приведены алгоритмы для n = 2 и n = 3 соответственно. Настоящие лягушки обозначены T, виртуальные – F.
1 TT_FF
2 T_TFF
3 TFT_F
4 TFTF_
5 TF_FT
6 _FTFT
7 F_TFT
8 FFT_T
. FF_TT
1 TTT_FFF
2 TT_TFFF
3 TTFT_FF
4 TTFTF_F
5 TTF_FTF
6 T_FTFTF
7 _TFTFTF
8 FT_TFTF
9 FTFT_TF
10 FTFTFT_
11 FTFTF_T
12 FTF_FTT
13 F_FTFTT
14 FF_TFTT
15 FFFT_TT
. FFF_TTT
Головоломка может быть легко обобщена на случай с m и n лягушками разных видов. Общее количество необходимых ходов равно mn + m + n, из которых mn – количество прыжков, а m + n – число сдвигов.
Ответ: для 3 лягушек с каждой стороны достаточно 15 ходов.
Ответ на вопрос со звёздочккой: Для m и n лягушек достаточно mn + m + n ходов.
Как ответили читатели Библиотеки программиста? Сам ответ о числе переходов первым дал пользователь wil4, но без указания решения:
15 для n=3
Первым ответ с решением, но с чуть большим числом ходов дал пользователь mr.fantazylight:

В комментариях к решению задачи мы обсудили, откуда берутся два лишних хода.
Программное решение, находящее алгоритм для любого m и n, реализовал на С++ пользователь krotbsod. Вот пример для m = 3 и n = 5:
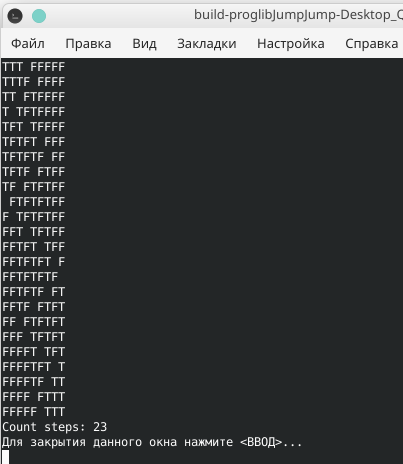
Автор решения krotbsod будет рад получить комментарии относительно кода: https://pastebin.com/Qm3Ru08L.
#include <iostream>
#include <cstring>
using namespace std;
//!!! P.S. Некоторые проверки в программе не выполняются, для упрощения восприятия
/**
* @brief Генерируем лягушек
* @param frogs Указатель на массив с лягушками [m + n + 1] размерности
* @param m T лягушек
* @param n F лягушек
**/
void generateFrogs(char *frogs, const int m , const int n) {
int count = m + n + 1;
memset(frogs, ' ', count);
for(int i = 0; i < m; i++) {
frogs[i] = 'T';
}
for(int i = m + 1; i < count; i++) {
frogs[i] = 'F';
}
}
/**
* @brief Заданные шаблоны поведения лягушек возле свободной ячейки
*/
struct Patterns{
public:
// T1 <-- Цифра - количество шагов
// ^
// |
// Символ - тип лягушки
/**
* @brief Задаем шаблоны в конструкторе структуры и записываем указатели в m_list
*/
Patterns() {
m_list[0] = "TF FT"; // T2
m_list[1] = "FT TF"; // F2
m_list[2] = "FF FT"; // F1
m_list[3] = "TT TF"; // F2
m_list[4] = "FF TF"; // F2
m_list[5] = "TT FT"; // T1
m_list[6] = "TF FF"; // T2
m_list[7] = "FT TT"; // T1
m_list[8] = "FT FF"; // F1
m_list[9] = "TF TT"; // T2
m_list[10] = "FT FT"; // F1 or T1
m_list[11] = "TF TF"; // lock
m_list[12] = "TT FF"; // F1 or T1
m_list[13] = "FF FF"; // F1;
m_list[14] = "TT TT"; // T1;
m_list[15] = "FF TT"; // done
}
/**
* @brief Возвращает указатель на заданный шаблон.
* Нужна лишь для итеративного поиска.
* @param num Номер шаблона в m_list
* @return Указатель на заданный шаблон
*/
const char *pattern(const int &num) {
// Проверку не стал делать, для упрощения восприятия
return m_list[num];
}
/**
* @brief Возвращает число шаблонов
* @return Число шаблонов
*/
int size() {
return m_size;
}
private:
static const int m_size = 16;
// Массив с указателями на массивы шаблонов
const char *m_list[m_size];
} frog_patterns;
/**
* @brief Получение текущего состояния (шаблона) в массиве с лягушками
* @param currentPattern Указатель на формируемый массив для записи в него шаблона
* @param frogs Указатель на массив с лягушками
* @param count Размер массива с лягушками
* @param iter Текущее положение пробела
*/
void getCurrentPattern(char *currentPattern, char *frogs, const int &count, const int &iter) {
//Задаем шаблон текущего положения для последующего сравнения с заданными шаблонами
memcpy(currentPattern, &frogs[iter - 2], 5); // dangerous !!! Опасно, выходим за рамки заданного массива. Но работает
// Задаем МНИМЫХ лягушек в текущий шаблон для последующего сравнения с заданными шаблонами.
// Когда символ пробела находится с краю, например: 'FF |' или '|T FF' (где | край массива)
// То приходим в несколько неодназначную ситуацию.
// Проще всего этого избежать добавив МНИМЫХ лягушек в шаблон для сравнения.
// Для конечных точек характеры следующие МНИМЫЕ лягушки: Для начального положения(крайнего левого предела) характерна мнимая F
// Для последнего положения(крайнего правого предела) характерна мнимая T
// P.S. МНИМЫЕ лягушки на то и мнимые, они ни как не дополняют исходный массив, они лишь заполняют шаблон для сравнения.
if(iter == 0) {
currentPattern[0] = 'F';
currentPattern[1] = 'F';
}
if(iter == 1) {
currentPattern[0] = 'F';
}
if(iter == (count - 1)) {
currentPattern[3] = 'T';
currentPattern[4] = 'T';
}
if(iter == (count - 2)) {
currentPattern[4] = 'T';
}
}
/**
* @brief Перемещение лягушки на место пустой ячейки
* @param frogs Указатель на массив с лягушками
* @param iter Текущее положение пробела
* @param type Тип лягушки
* @param step Шаг для перемещения лягушки
*/
void moveFrog(char *frogs, const int &iter, const char &type, const int &step) {
if(type == 'F') {
frogs[iter] = frogs[iter + step];
frogs[iter + step] = ' ';
}
if(type == 'T') {
frogs[iter] = frogs[iter - step];
frogs[iter - step] = ' ';
}
}
/**
* @brief Основной цикл сравнения состояний
* @param frogs Указатель на массив с лягушками
* @param m T лягушек
* @param n F лягушек
* @param iter Текущее положение пробела
* @return Возвращает 1, если перемещение всех лягушек завершено. В остальных случаях 0.
*/
int move(char *frogs, const int &m , const int &n, const int &iter) {
int count = m + n + 1;
char currentPattern[5];
memset(currentPattern, ' ', 5);
getCurrentPattern(currentPattern, frogs, count, iter);
// Проходим по всем заданным шаблонам
for(int i = 0; i < frog_patterns.size(); i++) {
// Сравниваем
int rescmp = memcmp(currentPattern, frog_patterns.pattern(i), 5);
if(rescmp == 0) {
// При совпадении перемещаем
switch (i) {
case 0:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 1:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 2:
moveFrog(frogs, iter, 'F', 1); // F1
break;
case 3:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 4:
moveFrog(frogs, iter, 'F', 2); // F2
break;
case 5:
moveFrog(frogs, iter, 'T', 1); // T1
break;
case 6:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 7:
moveFrog(frogs, iter, 'T', 1); // T1
break;
case 8:
moveFrog(frogs, iter, 'F', 1); // F1
break;
case 9:
moveFrog(frogs, iter, 'T', 2); // T2
break;
case 10:
moveFrog(frogs, iter, 'F', 1); // F1 or T1
break;
case 12:
if((m % 2) == 0) {
moveFrog(frogs, iter, 'T', 1);
} else {
moveFrog(frogs, iter, 'F', 1);
}
//moveFrog(frogs, iter, 'F', 1); // F1 or T1 //if m is even use T1
break;
case 13:
moveFrog(frogs, iter, 'F', 1);
break;
case 14:
moveFrog(frogs, iter, 'T', 1);
break;
case 15:
return 1;
break;
}
}
}
return 0;
}
/**
* @brief Запуск цикла алгоритма
* @param m T лягушек
* @param n F лягушек
*/
void jumpAlg(const int m , const int n) {
int count = m + n + 1;
char frogs[count + 1]; // +1 чтобы добавить символ \0 в конец, для корректного вывода через printf
frogs[count] = '\0'; // тут и добавим
generateFrogs(frogs, m, n); // Генерируем массив с лягушками
int counter = 0;
while(true) {
printf("%s\n", frogs);
int ret = 0;
for(int iter = 0; iter < count; iter++) {
// При нахождении пробела, входим в Основной цикл сравнения состояний
if(frogs[iter] == ' ') {
ret = move(frogs, m, n, iter);
break;
}
}
if(ret == 1) {
printf("Count steps: %d\n", counter);
break;
}
counter++;
}
}
int main()
{
//
// T, F
jumpAlg(3, 5);
return 0;
}
Спасибо, что присылаете в комментарии свои ответы и решения!




Комментарии