Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Полиномиальное хеширование
Хеширование строк позволяет эффективно отвечать на вопрос о равенстве строк, сравнивая их хеш-коды. Хеш-код – целое число, вычисляемое по символам строки. Если две строки равны, то их хеш-коды тоже равны.
Рассмотрим полиномиальное хеширование строк, при котором хеш-функция вычисляется как перевод из n-ичной системы в десятичную. Пусть дана строка s, основание BASE и кольцо вычетов по модулю MOD.
Тогда хеш-код строки вычисляется следующим образом:(s[0] * BASE0 + s[1] * BASE1 + ... + s[n – 1] * BASE(n-1)) % MOD
Или же наоборот: (s[0] * BASE(n-1) + s[1] * BASE(n-2) + .. + s[n – 1] * BASE0) % MOD
Выбор направления расстановки степеней не принципиален. Главное – использовать такое простое основание BASE, чтобы оно было взаимно простым с MOD, и его значение было больше количества символов в алфавите. MOD также должен быть простым, как правило, он равен 109 + 7 или 109 + 9.
Получение индекса символа s[i] в алфавите. В C++ обычно делают так: (int)s[i] – 'a' + 1. Но чтобы не загрязнять код, можно поступить проще, например, использовать приведение к signed char, который вернёт значение от 0 до 255. Важно помнить, что основание должно быть больше максимального значения возвращаемого кода, поэтому возьмём BASE = 2011 или 2017.
Чтобы иметь возможность получать хеш любой подстроки s[l..r] строки s за O(1), воспользуемся хеш-функцией на префиксах. Рассмотрим её подробнее. Пусть максимальная длина строки – 106. Заведём массив hash[SIZE], хранящий 64-битовые числа. Далее заполняем массив простейшей динамикой по вышеописанным формулам.
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 100100;
const int BASE = 2017;
const int MOD = 1000000009;
int64_t hash[SIZE];
void init_hash(const string &line, int64_t *h, int base, int mod)
{
h[0] = 0;
int n = line.length();
for (int i = 1; i <= n; ++i)
{
h[i] = h[i - 1] * base % mod + (signed char)line[i - 1] % mod;
}
}
Также понадобится массив степеней выбранного BASE. Заведём powers[SIZE], хранящий 64-битовые числа и заполним его по динамике: powers[i] = powers[i – 1] * BASE % MOD.
int64_t powers[SIZE];
void init_powers(int64_t *p, int base, int mod)
{
p[0] = 1;
for (int i = 1; i < SIZE; ++i)
{
p[i] = p[i - 1] * base % mod;
}
}
Рассмотрим получение хеша подстроки. Принцип такой же, как и при запросе суммы на диапазоне. От хеша с индексом r отнимаем хеш с индексом l, умноженный на BASE в степени разности r и l.
int64_t get_hash(int l, int r, int64_t *h, int64_t *p, int mod)
{
return (h[r] - h[l] * p[r - l] % mod + mod) % mod;
}
Вот и всё, можем пользоваться хешированием. Рассмотрим использование на простой задаче и проверим, что всё работает. Пусть нам даны две строки, a и b, q запросов, в которых даны границы подстрок: l1, r1, l2, r2 для первой и второй строки соответственно. Требуется ответить, равны ли подстроки.
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 100100;
const int BASE = 2017;
const int MOD = 1000000009;
int64_t ahash[SIZE];
int64_t bhash[SIZE];
int64_t powers[SIZE];
void init_powers(int64_t *p, int base, int mod)
{
p[0] = 1;
for (int i = 1; i < SIZE; ++i)
{
p[i] = p[i - 1] * base % mod;
}
}
void init_hash(const string &line, int64_t *h, int base, int mod)
{
h[0] = 0;
int n = line.length();
for (int i = 1; i <= n; ++i)
{
h[i] = h[i - 1] * base % mod + (signed char)line[i - 1] % mod;
}
}
int64_t get_hash(int l, int r, int64_t *h, int64_t *p, int mod)
{
return (h[r] - h[l] * p[r - l] % mod + mod) % mod;
}
int main()
{
string a, b;
cin >> a >> b;
init_powers(powers, BASE, MOD);
init_hash(a, ahash, BASE, MOD);
init_hash(b, bhash, BASE, MOD);
int q;
cin >> q;
while (q--)
{
int al, ar, bl, br;
cin >> al >> ar >> bl >> br;
--al; --bl;
if (get_hash(al, ar, ahash, powers, MOD) == get_hash(bl, br, bhash, powers, MOD))
{
cout << "YES\n";
}
else
{
cout << "NO\n";
}
}
return 0;
}
Теперь поговорим про один серьёзный недостаток полиномиального хеширования, а именно, коллизии. Коллизия – ситуация, когда строки по факту различны, но их хеши совпадают. В таком случае алгоритм заключает, что строки одинаковы, хотя на самом деле это не так.
Избавиться от коллизий при длине строк ~106 невозможно, потому что количество различных строк больше количества различных хеш-кодов. Вероятность коллизии можно свести к минимуму (почти к нулю), если написать ещё один хеш, т. е. написать первый хеш с основанием 2011 по модулю 109 + 7, а второй хеш – с основанием 2017 по модулю 109 + 9 и использовать оба хеша в сравнениях.
Алгоритм Кнута – Морриса – Пратта
Префикс-функция от строки s равна массиву P, где P[i] обозначает максимальную длину собственного (не совпадающего с полной строкой) префикса, равного собственному суффиксу. Говоря простым языком, мы идём по строке слева направо, добавляя s[i], и смотрим: есть ли префикс, совпадающий с суффиксом. Если да, то какова его максимальная длина.

"abacaba"В определённых случаях префиксы и суффиксы могут перекрываться, как, например, в строке "ABABABA".
Наивный алгоритм нахождения префикс-функции имеет сложность O(N3), что уже неприемлемо для строки длиной хотя бы 103.
Алгоритм Кнута – Морриса – Пратта (КМП) позволяет находить префикс-функцию от строки за линейное время, и имеет довольно лаконичную реализацию, по длине не превышающую наивный алгоритм.
Заметим важное свойство: P[i] <= P[i – 1] + 1. Префикс-функция от следующего элемента превосходит функцию от текущего не более чем на 1. Тогда в 0-индексации верно следующее свойство: s[i] = s[P[i – 1]] => P[i] = P[i – 1] + 1.
Рассмотрим случай, когда s[i] != s[P[i – 1]]: найдём такую длину j, что s[0..j-1] = s[i-j..i-1], но при этом j < P[i – 1]. Если s[i] = s[j], то P[i] = j + 1, тогда j = P[P[i – 1] – 1]. Иначе уменьшаем j по той же формуле: j = P[i – 1]. Пытаемся найти префикс, пока j != 0.
![s[14] != s[P[13]]; j = P[P[13] – 1] = 2; s[14] = s[2]; P[14] = j + 1 = 3](https://media.proglib.io/posts/2019/10/17/bb67e1aef2dfce45cff29f2b7b277186.jpg)
Теперь можем писать код. Будем использовать 1-индексацию, чтобы не путаться с лишними единицами:
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 100100;
int f[SIZE];
int main()
{
string line;
cin >> line;
f[0] = f[1] = 0;
for (int i = 1; i < line.length(); ++i)
{
int current = f[i];
while (current > 0 && line[current] != line[i])
{
current = f[current];
}
if (line[i] == line[current])
{
f[i + 1] = current + 1;
}
else
{
f[i + 1] = 0;
}
}
for (int i = 1; i <= line.length(); ++i)
{
cout << f[i] << " ";
}
return 0;
}
Префиксное дерево
Префиксное дерево (также бор, нагруженное дерево, англ. trie) – древовидная структура данных для хранения множества строк. Каждая строка представлена в виде цепочки символов, начинающейся в корне. Если у двух строк есть общий префикс, то у них будет общий корень и некоторое количество общих вершин. Построив префиксное дерево, можно эффективно отвечать на вопрос, содержится ли в множестве данных строк слово, которое нужно найти.
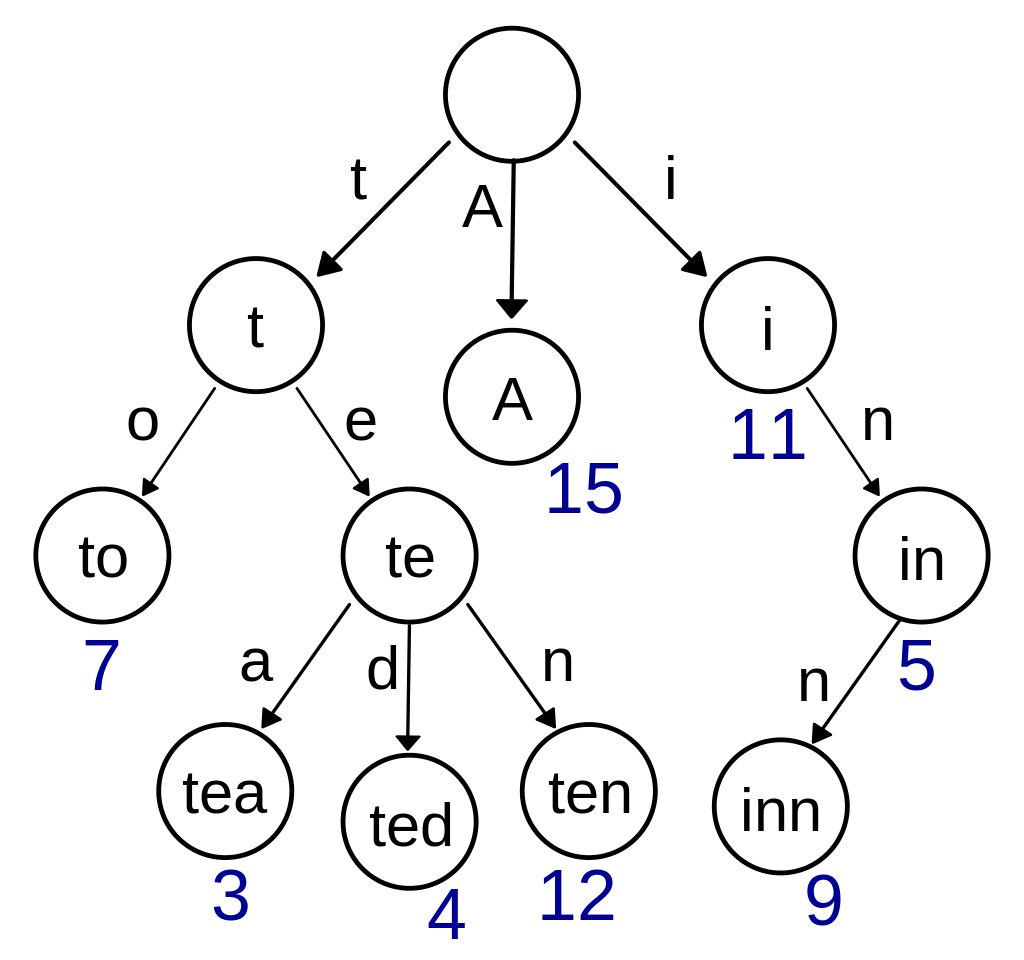
"to", 3 слова "tea", 4 слова "ted", 12 слов "ten", 9 слов "inn", 5 слов "in", 11 слов "i" и 15 слов "A"Принято считать, что бор – конечный детерминированный автомат, состояния которого – вершины подвешенного дерева. И правда – когда мы находимся в определённой вершине, т. е. в определённом состоянии, мы можем переместиться в другие по двум параметрам: текущей вершине v и нужному символу c. То есть, мы можем найти такую вершину v', которая обозначает самую длинную строку, состоящую из суффикса текущей вершины v и нужного символа c.
Будем писать бор с использованием структур таким образом, что каждой вершине будет соответствовать объект типа vertex, в котором будут храниться ссылки на следующие объекты (т. е. дочерние вершины) и количество строк, заканчивающихся в текущей вершине. Каждая вершина соответствует определённому символу. Поскольку бор – частный случай автомата, некоторые его вершины будут терминальными, а именно такие вершины, в которых количество заканчивающихся строк больше нуля. Для реализации нам понадобится динамическое выделение памяти.
#include <bits/stdc++.h>
using namespace std;
const int ALPHABET_SIZE = 26;
struct vertex
{
vertex* next[ALPHABET_SIZE]; // массив указателей на дочерние вершины
int strings_amount;
vertex(); // конструктор
};
vertex::vertex()
{
for (int i = 0; i < ALPHABET_SIZE; ++i) // изначально у текущей вершины не существует дочерних
{
next[i] = nullptr;
}
strings_amount = 0; // и не существует слов, оканчивающихся в ней
}
Напишем функцию добавления слова в бор. Корень дерева – root – пустая строка. Если в боре уже есть обрабатываемый символ, просто проходим по нему. Если такового нет – добавляем новую вершину.
vertex* root = new vertex();
void add_string(string &line)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i) // создаём все необходимые вершины, если они ещё не созданы
{
int symbol = line[i] - 'a';
if (current->next[symbol] == nullptr)
{
current->next[symbol] = new vertex();
}
current = current->next[symbol];
}
current->strings_amount++; // увеличиваем кол-во слов, заканчивающихся в последней вершине
}
Реализуем проверку на то, содержится ли слово в боре. Алгоритм схож с добавлением. Асимптотика такого поиска будет O(|S|).
bool has_a_string(string &line)
{
vertex* current = root; // начинаем идти от вершины
int n = line.length();
for (int i = 0; i < n; ++i) // идём по вершинам дерева в соответствии с символами в строке
{
current = current->next[line[i] - 'a'];
if (current == nullptr) // если такого символа нет в дереве, значит, проверяемого слова тоже нет в дереве, выходим
{
return false;
}
}
return current->strings_amount > 0;
}
Удаление можно реализовать «лениво», пройдясь до терминальной вершины и уменьшив количество слов, оканчивающихся в этой вершине.
void delete_string(string &line)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
current = current->next[line[i] - 'a'];
if (current == nullptr)
{
return;
}
}
current->strings_amount--;
}
Теперь напишем вывод всех слов, содержащихся в дереве. Для этого используем немного модифицированный DFS в сочетании с приёмом рекурсивного перебора.
string output = "";
void output_all_strings(vertex* current = root)
{
for (int i = 0; i < current->strings_amount; ++i)
{
cout << output << "\n";
}
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
if (current->next[i] != nullptr)
{
output.push_back('a' + i);
output_all_strings(current->next[i]);
output.pop_back();
}
}
}
Немного об асимптотике. Как было указано ранее, вставка элемента – O(|Si|), а получение всех ключей – O(k). Это делает бор более эффективной структурой данных по сравнению с обычным деревом, вставка у которого происходит за O(|S|log(k)), и с хеш-таблицей, получение всех ключей которой происходит за O(klog(k)). Но также важно помнить, что в определённых случаях префиксное дерево требует много памяти. Например, когда у всех слов, добавленных в бор, нет пересечений по префиксу, тогда структура будет использовать O(|S||Σ|) памяти, где |S| – сумма длин всех строк, а |Σ| – мощность алфавита.
Полный код:
#include <bits/stdc++.h>
using namespace std;
const int ALPHABET_SIZE = 26;
struct vertex
{
vertex* next[ALPHABET_SIZE];
int strings_amount;
vertex();
};
vertex::vertex()
{
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
next[i] = nullptr;
}
strings_amount = 0;
}
vertex* root = new vertex();
void add_string(string &line)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
int symbol = line[i] - 'a';
if (current->next[symbol] == nullptr)
{
current->next[symbol] = new vertex();
}
current = current->next[symbol];
}
current->strings_amount++;
}
void delete_string(string &line)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
current = current->next[line[i] - 'a'];
if (current == nullptr)
{
return;
}
}
current->strings_amount--;
}
bool has_a_string(string &line)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
current = current->next[line[i] - 'a'];
if (current == nullptr)
{
return false;
}
}
return current->strings_amount > 0;
}
string output = "";
void output_all_strings(vertex* current = root)
{
for (int i = 0; i < current->strings_amount; ++i)
{
cout << output << "\n";
}
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
if (current->next[i] != nullptr)
{
output.push_back('a' + i);
output_all_strings(current->next[i]);
output.pop_back();
}
}
}
int main()
{
int q;
cin >> q;
for (int req = 0; req < q; ++req)
{
char type;
cin >> type;
if (type == '1')
{
string word;
cin >> word;
add_string(word);
}
else if (type == '2')
{
string word;
cin >> word;
delete_string(word);
}
else if (type == '3')
{
string word;
cin >> word;
has_a_string(word) ? cout << "YES\n" : cout << "NO\n";
}
else if (type == '4')
{
cout << "\n";
output = "";
output_all_strings(root);
}
}
return 0;
}
Чтобы лучше понять, как работает префиксное дерево, можете «поиграться» с визуализацией работы структуры данных здесь.
Алгоритм Ахо – Корасик
Пусть дано множество неких строк/паттернов S = {s0, ... si, ... sn} и текст T. Необходимо найти все вхождения строк внутри текста.
Для решения необходимо построить автомат по бору (см. Алгоритм Ахо – Корасик). Мы уже написали функцию поиска строки в боре, которая решает похожую задачу. Но асимптотика такого решения O(n|si|), что неприемлемо.
Для решения поставленной задачи введём понятие суффиксной ссылки. Для начала обозначим, что [u] – строка, по которой мы пришли из корня в вершину u. Суффиксная ссылка вершины u p(u) – это указатель на такую вершину v, что [v] является суффиксом [u] максимальной длины.
Построение суффиксных ссылок
Во-первых, нам необходимо для каждой вершины хранить его предка, чтобы понимать, откуда и по какому символу мы пришли в неё.
Во-вторых, введём понятие перехода. Переход δ(v, c) – переход в боре из вершины v по символу c. В основе алгоритма лежит следующее равенство: p(u) = δ(p(u->parent), cu).
То есть, суффиксная ссылка текущей вершины – переход из вершины, в которую ведёт суффиксная ссылка предка текущей вершины, по символу текущей вершины. Грубо говоря, нужно пойти в предка, посмотреть, куда ведёт суффиксная ссылка (обозначим эту вершину за v'), перейти по ней, а затем попытаться перейти по символу. Если перехода из v' по символу c не существует, то справедливо следующее равенство: δ(v', c) = δ(p(v'), c) , т.е. от вершины, в которую вела суффиксная ссылка предка, нужно ещё раз пройти по суффиксной ссылке, и так вплоть до корня. Если из корня мы не можем перейти по символу c, то пропускаем его. Этот алгоритм справедлив, поскольку суффиксные ссылки всегда ведут в вершину дерева, которое меньше по глубине, следовательно, рано или поздно, мы сможем дойти до корня.
Реализация алгоритма
В каждой вершине помимо того, что мы хранили в обычном боре, будем хранить массив автоматных переходов go, суффиксную ссылку link , предка parent, последний символ parent_char, предыдущий суффикс prev для данной позиции, который является паттерном. Также будем хранить массив ind, который содержит индексы паттернов, оканчивающихся в этой вершине. Выглядит это всё так:
const int ALPHABET_SIZE = 26;
struct vertex
{
vertex* next[ALPHABET_SIZE];
vertex* go[ALPHABET_SIZE];
vertex* link = 0;
vertex* parent;
vertex* prev;
int parent_char;
vector<int> ind;
vertex();
vertex(int parent_char, vertex* parent);
};
vertex::vertex()
{
parent_char = 0;
parent = nullptr;
prev = nullptr;
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
next[i] = nullptr;
go[i] = nullptr;
}
}
vertex::vertex(int parent_char, vertex* parent)
{
this->parent_char = parent_char;
this->parent = parent;
prev = nullptr;
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
next[i] = nullptr;
go[i] = nullptr;
}
}
Добавление паттерна почти такое же, как и в обычном боре:
vertex* root = new vertex(-1, 0);
void add_string(string &line, int ind)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
int symbol = line[i] - 'a';
if (current->next[symbol] == nullptr)
{
current->next[symbol] = new vertex(symbol, current);
}
current = current->next[symbol];
}
current->ind.push_back(ind);
}
Поскольку мы утверждаем, что при использовании суффиксных ссылок, они ведут в меньшее по глубине дерево, суффиксные ссылки и автоматные переходы можно посчитать динамическим программированием. Подсчитывать динамики go и link будем «лениво»: введём для них две функции, которые будут мемоизировать результат выполнения.
vertex* go(vertex* current, int c);
vertex* link(vertex* current)
{
if (!current->link)
{
if (current == root || current->parent == root) // если длина строки < 2, то суффиксная ссылка - корень
{
current->link = root;
}
else
{
current->link = go(link(current->parent), current->parent_char); // в остальных случаях применяем формулу
}
}
return current->link;
}
vertex* go(vertex* current, int c)
{
if (!current->go[c])
{
if (current->next[c]) // если обычный переход есть, то автоматный должен вести туда же
{
current->go[c] = current->next[c];
}
else if (current == root) // если нет перехода из корня, делаем петлю
{
current->go[c] = root;
}
else
{
current->go[c] = go(link(current), c); // в остальных случаях применяем формулу
}
}
return current->go[c];
}
Напишем функцию получения суффикса prev, который является паттерном:
vertex* prev(vertex* current)
{
if (current == root)
{
return nullptr;
}
if (!current->prev)
{
if (link(current)->ind.size() != 0)
{
current->prev = link(current);
}
else
{
current->prev = prev(link(current));
}
}
return current->prev;
}
Теперь напишем main. Нам нужно ввести n паттернов, добавив их в бор, текст и для каждого паттерна вывести его границы в тексте. Заведём вектор векторов ans, в котором для каждого i-го паттерна будем хранить его правую границу каждого j-го вхождения в текст.
Далее необходимо пройти по тексту, для каждого символа сделать автоматный переход. Каждый паттерн, который оканчивается вершиной, в которую был совершён автоматный переход, добавляем в ans. Пока будет существовать суффикс, prev который будет являться паттерном, будем переходить в него. Затем выведем все вхождения. Код:
int main()
{
int n;
cin >> n;
vector<string> patterns;
for (int i = 0; i < n; i++)
{
string s;
cin >> s;
add_string(s, i);
patterns.push_back(s);
}
string text;
cin >> text;
vector<vector<int>> ans(n);
vertex* cur = root;
for (int i = 0; i < text.size(); i++)
{
cur = go(cur, text[i] - 'a');
vertex* cur_ans = cur;
while (cur_ans)
{
for (int ind: cur_ans->ind)
{
ans[ind].push_back(i + 1);
}
cur_ans = prev(cur_ans);
}
}
for (int i = 0; i < n; i++)
{
cout << patterns[i] << " : ";
int psize = patterns[i].size();
if (ans[i].size() == 0)
{
cout << "no matching";
}
else
{
for (int j: ans[i])
{
cout << j - psize + 1 << " - " << j << "; ";
}
}
cout << endl;
}
return 0;
}
Весь код:
#include <bits/stdc++.h>
using namespace std;
const int ALPHABET_SIZE = 26;
struct vertex
{
vertex* next[ALPHABET_SIZE];
vertex* go[ALPHABET_SIZE];
vertex* link = 0;
vertex* parent;
vertex* prev;
int parent_char;
vector<int> ind;
vertex();
vertex(int parent_char, vertex* parent);
};
vertex::vertex()
{
parent_char = 0;
parent = nullptr;
prev = nullptr;
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
next[i] = nullptr;
go[i] = nullptr;
}
}
vertex::vertex(int parent_char, vertex* parent)
{
this->parent_char = parent_char;
this->parent = parent;
prev = nullptr;
for (int i = 0; i < ALPHABET_SIZE; ++i)
{
next[i] = nullptr;
go[i] = nullptr;
}
}
vertex* root = new vertex(-1, 0);
void add_string(string &line, int ind)
{
vertex* current = root;
int n = line.length();
for (int i = 0; i < n; ++i)
{
int symbol = line[i] - 'a';
if (current->next[symbol] == nullptr)
{
current->next[symbol] = new vertex(symbol, current);
}
current = current->next[symbol];
}
current->ind.push_back(ind);
}
vertex* go(vertex* current, int c);
vertex* link(vertex* current)
{
if (!current->link)
{
if (current == root || current->parent == root)
{
current->link = root;
}
else
{
current->link = go(link(current->parent), current->parent_char);
}
}
return current->link;
}
vertex* go(vertex* current, int c)
{
if (!current->go[c])
{
if (current->next[c])
{
current->go[c] = current->next[c];
}
else if (current == root)
{
current->go[c] = root;
}
else
{
current->go[c] = go(link(current), c);
}
}
return current->go[c];
}
vertex* prev(vertex* current)
{
if (current == root)
{
return nullptr;
}
if (!current->prev)
{
if (link(current)->ind.size() != 0)
{
current->prev = link(current);
}
else
{
current->prev = prev(link(current));
}
}
return current->prev;
}
int main()
{
int n;
cin >> n;
vector<string> patterns;
for (int i = 0; i < n; i++)
{
string s;
cin >> s;
add_string(s, i);
patterns.push_back(s);
}
string text;
cin >> text;
vector<vector<int>> ans(n);
vertex* cur = root;
for (int i = 0; i < text.size(); i++)
{
cur = go(cur, text[i] - 'a');
vertex* cur_ans = cur;
while (cur_ans)
{
for (int ind: cur_ans->ind)
{
ans[ind].push_back(i + 1);
}
cur_ans = prev(cur_ans);
}
}
for (int i = 0; i < n; i++)
{
cout << patterns[i] << " : ";
int psize = patterns[i].size();
if (ans[i].size() == 0)
{
cout << "no matching";
}
else
{
for (int j: ans[i])
{
cout << j - psize + 1 << " - " << j << "; ";
}
}
cout << endl;
}
return 0;
}
Другие задачи на алгоритм Ахо – Корасик:
Эта статья написана читателем Библиотеки программиста – не стесняйтесь присылать свои публикации! 🐸 Если статья оказалась для вас трудной, посмотрите наш пост про книги по C++. Cреди перечисляемых есть книги с уклоном на алгоритмы. Больше статей по теме – по тегу Алгоритмы.



Комментарии