🅾️ Что такое «О» большое: объясняем на простых примерах

Что такое «О» большое

«О» большое (Big O notation) — это математическая нотация, которая позволяет оценить, как изменяется время выполнения алгоритма или объем используемой памяти в зависимости от размера входных данных. Есть еще «о» малое — эта нотация дает более строгую верхнюю границу для сложности алгоритма, но часто ее труднее вычислить, чем «О» большое. На практике «О» большое используется чаще, поскольку эта концепция проще для анализа и дает достаточно хорошую оценку сложности в большинстве случаев.

Зачем нужно «О» большое

Понимание этой нотации позволяет:

• Сравнивать эффективность различных алгоритмов для решения одной и той же задачи.
• Прогнозировать поведение алгоритма при увеличении размера входных данных.
  
• Оптимизировать код путем идентификации и улучшения сложных алгоритмов.
• Выбирать оптимальные структуры данных и алгоритмы при решении ресурсоемких задач.
  

Эффективность алгоритмов: временная и пространственная сложность

Обычно эффективность алгоритмов оценивается по двум критериям:

• Время выполнения. Временная сложность — это количество операций, которые должен выполнить алгоритм. Она показывает, как растет время выполнения алгоритма при увеличении входных данных.
• Объем используемой памяти. Пространственная сложность алгоритма измеряет объем памяти, которую он использует в зависимости от размера входных данных. На пространственную сложность влияют несколько факторов, включая количество переменных, тип и размер структуры данных, вызовы функций и способ выделения памяти.

Как «О» большое описывает эффективность алгоритмов

Итак, «О» большое — это способ оценить, как время выполнения алгоритма или требуемый объем памяти растут с увеличением размера входных данных.

Пример: предположим, что стоматолог тратит 30 минут на прием одного пациента. По мере увеличения очереди пациентов, время, необходимое для приема всех пациентов, будет расти линейно пропорционально количеству пациентов в очереди.

Учитывая это, мы можем охарактеризовать эффективность стоматолага как линейную. В нотации большого «О» эта эффективность выглядит как O(n), где n равно количеству пациентов, а время, необходимое стоматологу для завершения работы, растет линейно или пропорционально количеству пациентов:

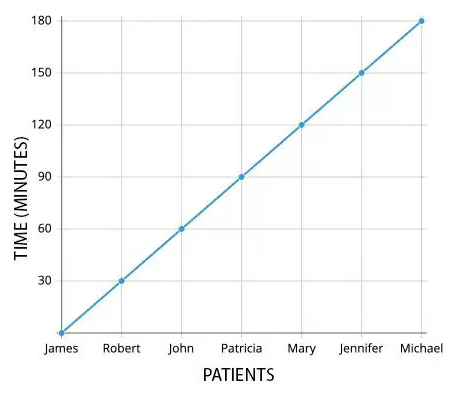
Эффективность стоматолога можно описать этой функцией:

        var time = 0;
const patients = ['James', 'Robert', 'John', 'Patricia', 'Mary', 'Jennifer', 'Michael'];

function calculateTime() {
  for(let i = 0; i < patients.length; i++){
    time += 30;
  }
  console.log("Total Time 👉 ", time);
}
    

Здесь функция calculateTime служит простым примером для иллюстрации концепции большого «О» и потому не выполняет вычисления, умножая пациентов на затраченное на них время. Временная сложность этой функции O(n), а сложность вывода в консоль O(1):

        function calculateTime() {
  for(let i = 0; i < patients.length; i++){ // 👉 O(n)
    time += 30; // 👉 O(1)
  }
  console.log("Total Time 👉 ", time); // 👉 O(1)
}
    

Разберемся, как именно можно определить сложность любого алгоритма.

Курс «Алгоритмы и структуры данных»

Курс «Алгоритмы и структуры данных» для тех, кто хочет научиться работать с алгоритмами, подготовиться к собеседованию в технологическую компанию или участвовать в сложных проектах.

После изучения вы:

• Узнаете о популярных алгоритмах и структурах данных
• Получите практический опыт решения сложных алгоритмических задач
  
• Сможете легко пройти техническое собеседование
  

До 5 мая 2024 включительно на курс действует скидка -40%.

Программа обучения

• Введение. Производительность алгоритмов
• Работа с числами
  
• Массивы
  
• Списки. Стек, очередь, дек
  
• Очередь с приоритетом
  
• Основы сортировки
  
• Порядковые статистики
  
• Деревья
  
• Хеш-таблицы
  
• Жадные алгоритмы. Динамическое программирование
  
• Графы и рекурсия
  
• Строки
  
• Криптография
  
• Длинные числа. Итоги
  

Основные правила вычисления большого «О»

Три главных правила вычисления большого «О» включают:

• Определение худшего случая.
  
• Исключение постоянных величин.
• Игнорирование всех процессов, которые выполняются быстрее (или затрачивают меньше памяти), чем самая медленная и тяжелая часть алгоритма.

Рассмотрим все эти правила подробнее.

Худший случай

При анализе алгоритмов выделяют три случая — лучший, средний и худший:

• Лучший случай показывает, как быстро алгоритм выполняется для определенного входного значения. В примере с функцией findJoey, которая ищет Joey в массиве друзей, лучший случай происходит, когда Joey находится в начале массива. В этом случае алгоритм выполнится всего один раз, поскольку сразу же найдет имя и прервет цикл с помощью оператора break. Таким образом, время выполнения функции в лучшем случае составляет O(1), что означает константное время выполнения.

        let friends = ['Joey', 'Rachel', 'Phoebe', 'Ross', 'Monica', 'Chandler'];

function findJoey(){
  for(let i = 0; i < friends.length; i++){
    if(friends[i] === 'Joey'){
      console.log("Found!");
      break;
    }
  }
} 
    

• Средний случай представляет собой прогноз о времени выполнения алгоритма, когда входные данные являются случайными. В функции findJoey, где Joey может находиться в любом месте массива, средний случай будет зависеть от того, где именно находится Joey. Если Joey находится в середине массива, алгоритм должен будет пройти половину массива, чтобы найти его, что приведет к времени выполнения O(n/2), где n — количество элементов в массиве.

        let friends = ['Rachel', 'Phoebe', 'Ross', 'Joey', 'Monica', 'Chandler'];

function findJoey(){
  for(let i = 0; i < friends.length; i++){
    if(friends[i] === 'Joey'){
      console.log("Found!");
      break;
    }
  }
} 
    

• Худший случай означает, как долго алгоритм может выполниться для предоставленного входного значения. В примере с функцией findJoey, где Joey находится в конце массива, алгоритму придется пройти через весь массив, чтобы найти имя. В этом случае время выполнения алгоритма составляет O(n), где n — количество элементов в массиве.

Исключение постоянных величин

При расчете сложности алгоритма нет необходимости учитывать константы. Для примера снова вернемся к функции findJoey, которая ищет Joey в массиве друзей:

        let friends = ['Rachel', 'Phoebe', 'Ross', 'Monica', 'Chandler', 'Joey'];

function findJoey(){
  for(let i = 0; i < friends.length; i++){ // O(n)
    console.log("Step 👉", i + 1); // O(1)

    if(friends[i] === 'Joey'){ // O(1)
      console.log("Found!"); // O(1) 
    }
  }
} 
    

Просуммируем сложность выполнения отдельных шагов:

        Сложность = O(n) + O(1) + O(1) + O(1)
           = O(n) + O(3)
           = O(n + 3)
    

После упрощения сложность равна O(n + 3). Однако, при расчете эффективности функции, время выполнения константных операций не имеет значения. Это связано с тем, что даже если массив будет очень большим, например, содержать 2 миллиона элементов, эти константные операции не повлияют на общую эффективность функции, так как основной объем работы все равно будет заключаться в итерации по массиву:

        Реальная сложность = O(n + 3)
                   = O(n)
    

Примечание: если функция состоит только из операций с константами, то ее сложность будет константной. Например, функция steps, которая выводит три уведомления, имеет реальную сложность O(3). Но по правилам большого «О» мы определяем ее сложность как O(1), так как предполагаем, что она всегда будет выполняться за одинаковое время:

        function steps(){
  console.log("Step 1"); // O(1)
  console.log("Step 2"); // O(1)
  console.log("Step 3"); // O(1)
}
    

Игнорирование всех недоминирующих процессов

С увеличением времени выполнения и/или объема потребления памяти эффективность алгоритмов снижается. В нотации большого «О» эта иерархия выглядит так:

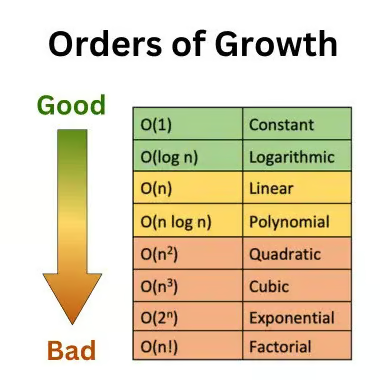
При оценке алгоритма его итоговой сложностью является сложность самого медленного шага. Поэтому при оценке этой функции мы считаем ее сложностью O(n), и игнорируем процессы О(1):

        let friends = ['Rachel', 'Phoebe', 'Ross', 'Monica', 'Chandler', 'Joey'];

function findJoey(){
  for(let i = 0; i < friends.length; i++){ // O(n)
    console.log("Step 👉", i + 1); // O(1)

    if(friends[i] === 'Joey'){ // O(1)
      console.log("Found!"); // O(1) 
    }
  }
} 
    

Основные классы сложности алгоритмов

Классов сложности алгоритмов много, здесь мы рассмотрим только самые основные:

• O(1) — константное время. Это означает, что время выполнения алгоритма остается постоянным, независимо от размера входных данных. Пример: доступ к элементу массива по индексу.
• O(log n) — логарифмическое время. Время выполнения алгоритма увеличивается логарифмически по отношению к размеру входных данных. Пример: бинарный поиск в отсортированном массиве.
  
• O(n) — линейное время. Время выполнения алгоритма прямо пропорционально размеру входных данных. Пример: итерация по массиву.
  
• O(n log n) — линейно-логарифмическое время. Время выполнения алгоритма растет растет пропорционально произведению размера входных данных на логарифм этого размера. Пример: сортировка слиянием.
  
• O(n^2) — квадратичное время. Время выполнения алгоритма растет как квадрат размера входных данных. Пример: вложенный цикл, где каждый элемент массива сравнивается с каждым другим элементом.
  
• O(2^n) — экспоненциальное время. Время выполнения алгоритма растет экспоненциально по отношению к размеру входных данных. Пример: рекурсивный алгоритм, который решает задачу путем разделения ее на подзадачи.
  
• O(n!) — факториальное время. Время выполнения алгоритма растет как факториал размера входных данных. Пример: задача коммивояжера, где необходимо найти самый короткий маршрут, проходящий через все города.
  
• O(m+n) и O(mn). В первом случае время выполнения алгоритма растет линейно по отношению к размеру входных данных, а во втором случае время выполнения будет квадратичным. Примеры: линейный поиск в двумерном массиве имеет сложность O(mn), а объединение двух отсортированных списков в общий отсортированный список выполняется за O(m + n).

Представить эффективности этих классов можно так:

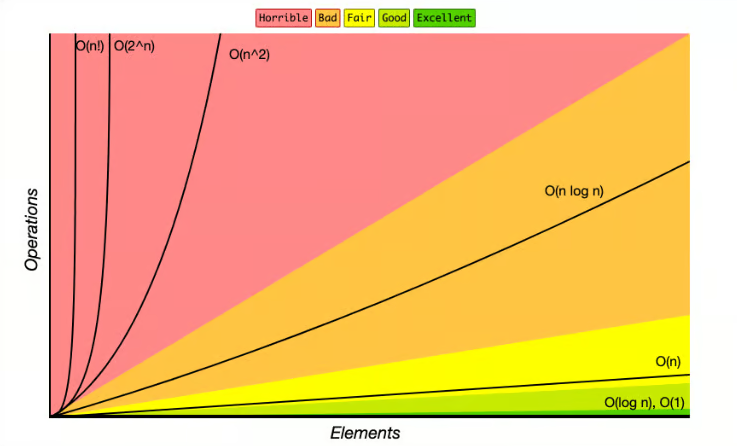
А теперь рассмотрим основные примеры временной и пространственной сложности подробнее.

Временная сложность

O(1) — константное время

Константное время выполнения означает, что время выполнения алгоритма не зависит от размера входных данных. Время выполнения остается постоянным, независимо от того, сколько элементов содержит массив или как много данных обрабатывает алгоритм. Это происходит потому, что алгоритм выполняет фиксированное количество операций, не зависящих от размера входных данных:

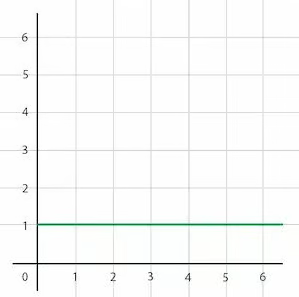
Примером константного времени выполнения может служить операция доступа к элементу массива по индексу. Например, если у вас есть массив friends и вы хотите вывести четвертый элемент массива, независимо от того, сколько элементов содержит массив, время выполнения этой операции останется постоянным — потому, что для доступа к элементу массива по индексу требуется выполнить только одну операцию, которая не зависит от размера массива:

        let friends = ['Rachel', 'Phoebe', 'Ross', 'Monica', 'Chandler', 'Joey'];

function printFourthIndex(){
  console.log(friends[3]); // O(1)
} 
    

O(log n) — логарифмическое время

Логарифмическое время выполнения означает, что время выполнения алгоритма увеличивается пропорционально логарифму размера входных данных, то есть очень медленно:

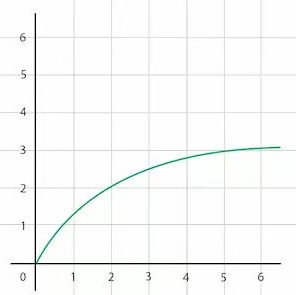
Примером алгоритма с логарифмическим временем выполнения может служить бинарный поиск. В бинарном поиске мы делим массив пополам на каждом шаге, пока не найдем искомый элемент. Таким образом, количество шагов, необходимых для поиска, растет логарифмически по отношению к размеру массива.

Вот простой пример функции на JavaScript, которая имеет логарифмическое время выполнения:

        // n = 8
function logNFunc(n){
  while(n > 1){ 
    n = Math.floor(n / 2); 
  }
}
    

Функция logNFunc работает так:

        n = 8

Итерация 1 = 8 / 2 = 4
Итерация 2 = 4 / 2 = 2
Итерация 3 = 2 / 2 = 1
    

То есть мы достигли 1 всего за 3 шага. Алгоритмы с логарифмическим временем выполнения очень эффективны: они могут обрабатывать большие объемы данных с относительно небольшим увеличением времени выполнения. На графике, приведенном выше, видно, что на больших числах кривая становится все более и более плоской, больше напоминая прямую константного времени.

O(n) — линейное время

Этот вариант мы уже рассматривали выше, в примере с пациентами стоматолога. Линейная временная сложность означает, что время выполнения алгоритма растет прямо пропорционально размеру входных данных — если размер входных данных увеличивается в 6 раз, время выполнения алгоритма также увеличится в 6 раз:

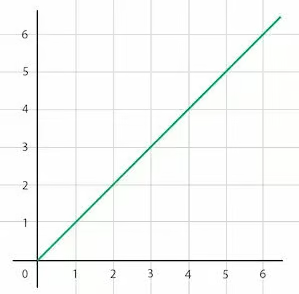
Примером алгоритма с линейной временной сложностью может служить простой цикл, который проходит через каждый элемент массива. Например, как в этой функции:

        function nFunc(n){
  for(let i = 0; i < n; i++){ 
    console.log("Step 👉", i + 1); 
  }
} 
    

Алгоритмы с линейной временной сложностью тоже считаются очень эффективными, хотя, как очевидно, при обработке очень больших объемов данных они уступают в эффективности алгоритмам с логарифмическим временем выполнения.

O(n log n) — линейно-логарифмическое время

Если объединить последние две временные сложности (логарифмическую и линейную), мы получаем линейно-логарифмическое время, которое иногда также называют псевдолинейным. Такое время выполнения часто встречается в алгоритмах, основанных на стратегии «разделяй и властвуй» — сортировка слиянием, быстрая сортировка и сортировка кучей.

Рассмотрим пример такого алгоритма:

        // n = 4
function nLogNFunc(n){
  let temp = n;
  while(n > 1){
    n = Math.floor(n/2);
    for(let i = 0; i < temp; i++){ 
      console.log("Step 👉", i + 1); 
    }
  }
} 
    

Сначала мы создаем переменную temp и присваиваем ей значение n, чтобы скопировать значение n в temp. Затем мы начинаем цикл while, в котором мы делим значение n пополам. На следующей строке у нас есть цикл for, который итерируется temp раз. Таким образом, временная сложность внешнего цикла равна O(log n), а внутреннего O(n):

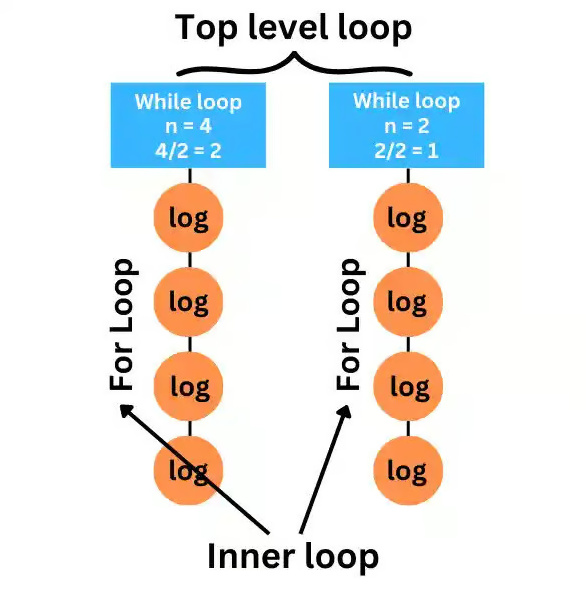
Итоговая сложность будет равна O(n log n):

        Итоговая сложность = O(n * log n);
                   = O(n log n);
    

Как видно по графику, при больших объемах данных логарифмическая часть функции растет довольно медленно, и в результате увеличение времени выполнения происходит почти линейно:

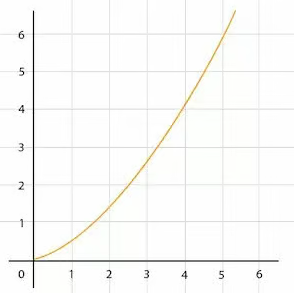
Линейно-логарифмическое время — последний класс сложности, который считается очень эффективным: все последующие типы алгоритмов работают гораздо медленнее.

O(n^2) — квадратичное время

Квадратичная временная сложность означает, что время выполнения алгоритма увеличивается пропорционально квадрату размера входных данных: если размер входных данных удваивается, время выполнения алгоритма увеличится в четыре раза. Примерами алгоритмов с квадратичной временной сложностью являются неэффективные алгоритмы сортировки — пузырьковая сортировка, сортировка вставками и сортировка выбором.

Рассмотрим на примере:

        // n = 4
function nSquaredNFunc(n){
 for(let j = 0; j < n; j++){
   for(let k = 0; k < n; k++){
     console.log(j, k);
   }
 }
} 
    

Эта функция принимает n в качестве аргумента. Внешний цикл будет выполнен n раз, где каждая итерация будет включать в себя выполнение внутреннего цикла. Внутренний цикл также будет выполнен n раз:

Эта матрица состоит из 4 строк и 4 столбцов, потому что n в нашем коде было равно 4. Подсчитаем количество шагов, необходимых для вывода матрицы 8х8:

        Временная сложность = n * n
                    = 8 * 8
                    = 64

    

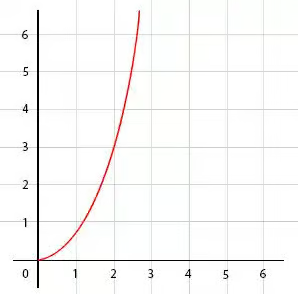
Как видно по графику, время выполнения функции растет гораздо быстрее, чем у алгоритма с линейно-логарифмической сложностью:

O(2^n) — экспоненциальное время

Экспоненциальная временная сложность означает, что время выполнения алгоритма увеличивается экспоненциально: даже небольшое увеличение размера входных данных приводит к значительному увеличению времени выполнения.

Рассмотрим функцию fib(n), которая вычисляет числа Фибоначчи с использованием рекурсии. В этой функции для каждого числа n вызываются две функции fib(n — 1) и fib(n — 2) :

        function fib(n){
  if(n === 0){
    return 0;
  }

  if(n === 1){
    return 1;
  }

  return fib(n - 1) + fib(n - 2)
}
    

Это приводит к тому, что количество вызовов функции удваивается на каждом уровне рекурсии. Например, на первом уровне функция вызывается два раза, на втором уровне — четыре раза, на третьем уровне — восемь раз и так далее:

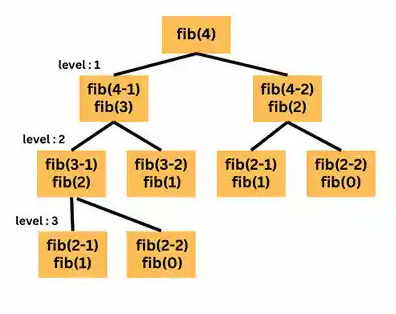
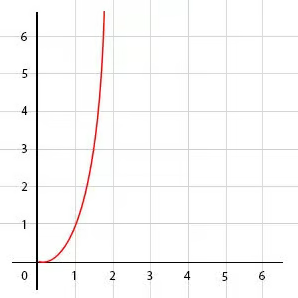
Временная сложность этой функции составляет O(2^n), поскольку количество вызовов функции удваивается на каждом уровне рекурсии, что делает функцию неэффективной для больших значений n. В целом, алгоритмы с экспоненциальной сложностью непригодны для работы с большими объемами данных:

O(n!) — факториальное время

Факториальное время подходит для решения реальных задач даже меньше, чем экспоненциальное, поскольку оно увеличивается гораздо быстрее.

Пример алгоритма с факториальной сложностью — функция, которая пытается найти все возможные перестановки набора элементов:

        function f(n){
  if(n === 0){
    return 0;
  }

  for(let i = 0; i < n; i++){
    f(n - 1);
  }
}
    

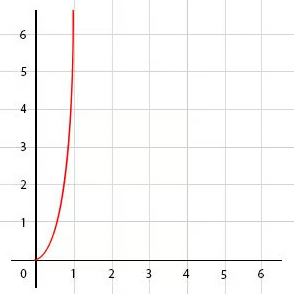
Количество таких перестановок растет факториально, что делает алгоритм совершенно непригодным для работы с большими объемами данных:

O(m+n) или O(mn)

Все рассмотренные выше примеры учитывали лишь один входной параметр. Но что, если таких параметров будет больше? В общем случае, если имеется алгоритм с несколькими входными параметрами, его сложность определяется как функция от этих параметров:

• Если операции выполняются последовательно для каждого входного параметра, сложность будет суммой их размеров, O(m + n).
• Если же операции вложены друг в друга (например, вложенные циклы), сложность будет произведением их размеров, O(mn).
  

О(m + n) означает, что время выполнения алгоритма зависит от суммы размеров входных данных m и n:

        function mn(m, n){
  for(let i = 0; i < m; i++){
    console.log("m => ", i);
  }

  for(let j = 0; j < n; j++){
    console.log("n => ", j);
  }
}
    

В этом примере первый цикл выполняется m раз, а второй — n раз. Следовательно, общее время выполнения функции пропорционально сумме m + n. Это означает, что сложность алгоритма является линейной относительно каждого из входных параметров и общая сложность равна O(m + n).

О(mn) означает, что время выполнения алгоритма зависит от произведения размеров входных данных m и n:

        function mn(m, n){
  for(let i = 0; i < m; i++){
    for(let j = 0; j < n; j++){
      console.log(i, j);
    }  
  }
}
    

Здесь внутренний цикл выполняется n раз для каждой итерации внешнего цикла, который выполняется m раз. Таким образом, общее количество операций, выполняемых функцией, равно m * n. Следовательно, сложность алгоритма является квадратичной относительно входных параметров и общая сложность равна O(mn).

Пространственная сложность

Эффективность алгоритмов определяется не только по времени выполнения, но и по объему использованной памяти (пространства в терминологии большого О).

O(1) — константное пространство

Константная пространственная сложность означает, что количество памяти, необходимое алгоритму, не зависит от размера входных данных. В этом примере используется только две переменных: n и result. Независимо от размера n, количество памяти, используемое этой функцией, остается постоянным:

        function constantSpace(n) {
    let result = n * n;
    console.log(result);
}
    

O(log n) — логарифмическое пространство

Пространственная сложность O(log n) означает, что количество памяти, необходимое алгоритму, растет логарифмически с увеличением размера входных данных. В этом примере используется бинарный поиск, и с каждой итерацией цикла размер данных уменьшается вдвое:

        function binarySearch(array, x) {
    let start = 0, end = array.length - 1;

    while (start <= end) {
        let mid = Math.floor((start + end) / 2);

        if (array[mid] === x) return true;

        else if (array[mid] < x) 
             start = mid + 1;
        else
             end = mid - 1;
    }

    return false;
}
    

O(n) — линейное пространство

Линейная пространственная сложность означает, что количество памяти, необходимое алгоритму, увеличивается пропорционально размеру входных данных:

        function linearSpace(n) {
    let array = [];
    for(let i = 0; i < n; i++) {
        array[i] = i;
    }
    console.log(array);
}
    

O(n^2) — квадратичное пространство

Алгоритмы с квадратичной пространственной сложностью используют объем памяти, который растет квадратично по мере увеличения размера входных данных. Пространственная сложность этого примера составляет O(n^2), поскольку в функции создается матрица, размер которой равен n^2:

        function quadraticSpace(n) {
    let matrix = [];
    for(let i = 0; i < n; i++) {
        matrix[i] = [];
        for(let j = 0; j < n; j++) {
            matrix[i][j] = i + j;
        }
    }
    console.log(matrix);
}
    

Подведем итоги

Концепция большого «О» может показаться сложной на первый взгляд, но разобраться в ней необходимо: наивный подход к решению задач зачастую приводит к чрезмерно высокой временной и/или пространственной сложности, что делает такие решения непрактичными для использования в реальных масштабных проектах. Но выход есть:

• Несмотря на то, что для всесторонней оценки алгоритма и выбора оптимального решения необходим формальный математический анализ, при решении умеренно сложных задач часто достаточно оценки «на глаз». Например, если код использует вложенные циклы, наверняка его сложность будет квадратичной, а с каждым дополнительным вложенным циклом сложность будет увеличиваться. Если же решение использует рекурсию с несколькими вызовами на каждом уровне, то, скорее всего, речь идет об экспоненциальной сложности.
• Информатика и математика располагают богатейшим наследием оптимальных алгоритмов — выдающиеся умы уже разработали максимально эффективные решения для широкого спектра задач. Изучение и понимание этих алгоритмов, а также принципов, лежащих в их основе, жизненно важно для любого профессионального разработчика.
  

Инвестируя время в понимание вычислительной сложности и изучение существующих оптимальных алгоритмов, разработчики приобретают способность создавать действительно производительные, масштабируемые и ресурсоэффективные системы, которые могут справляться с самыми сложными задачами в реальном мире.

При подготовке статьи использовалась публикация Big O Notation: A Simple Explanation With Examples.