📈 Для чего нужен математический анализ в машинном обучении

Математический анализ – основа всей высшей математики. Он необходим во многих разделах царицы наук: особенно это относится к производным и интегралам. К запуску авторского «Онлайн-курса по математике в Data Science Lite» мы начинаем публикацию серии статей об использовании математических методов в науке о данных. Сегодня рассмотрим несколько самых очевидных применений матанализа в машинном обучении, а затем перейдем к линейной алгебре и теории вероятностей.

Градиентный спуск

Знак производной показывает, возрастает исходная функция (производная положительна) или убывает (отрицательна). Если производная существует и равна нулю, то мы находимся в точке экстремума (минимума или максимума).

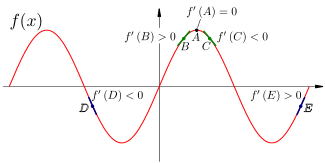
На этом свойстве производной основан самый популярный метод машинного обучения – градиентный спуск (и вообще практически все методы машинного обучения). Градиент функции нескольких переменных – это вектор ее частных производных по каждой из этих переменных:

В данном случае L – это функция потерь (Loss) нашей модели машинного обучения, а w₁,...w_n – внутренние параметры модели, которые должны изменяться в процессе ее обучения (веса). Функция потерь измеряет "качество" модели, она может быть очень разной в зависимости от задачи. Например, для модели, предсказывающей значение одной переменной, это может быть квадрат разности между истинным значением этой переменной и предсказанным.

Нам нужно найти глобальный минимум функции потерь в пространстве весов – то есть, такие значения весов, при которых модель будет оптимальной. Метод градиентного спуска на каждом шагу рассчитывает градиент в данной точке n-мерного пространства весов и переходит в следующую точку, двигаясь по направлению вектора градиента.

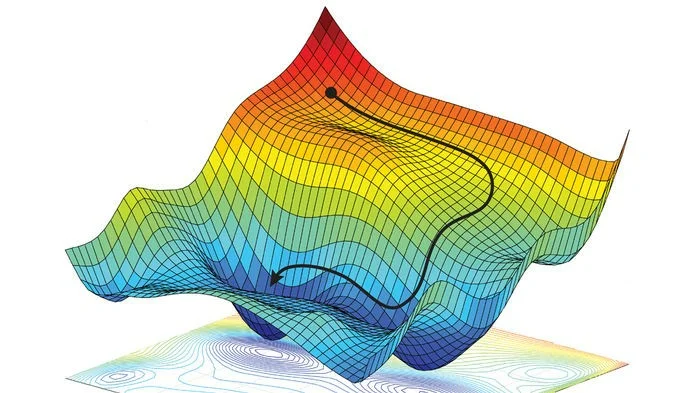
Идея метода градиентного спуска очень проста: «если идти все время вниз, то когда-нибудь достигнешь дна». Чтобы узнать, в каком направлении находится "низ", мы и считаем вектор градиента.

Цепное правило и back-propagation

Изучая математический анализ, вы познакомитесь с цепным правилом вычисления производной – это правило вычисления производной сложной функции:

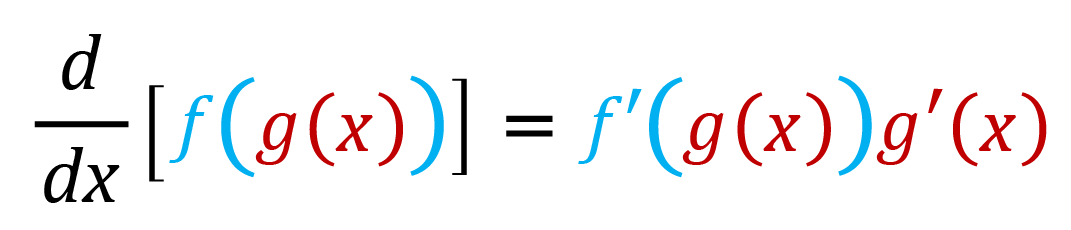
Поскольку все нейронные сети состоят из нескольких слоев, и входом каждого слоя сети, кроме первого, является выход предыдущего слоя, результат работы сети (прямого прохода) – это именно сложная функция, в которой функция активации нейронов каждого слоя выполняется над результатами функции активации предыдущего.

Для обучения нейронной сети нам нужно рассчитать градиент ее функции потерь, то есть набор производных этой функции по всем весам сети. Как видно на следующем рисунке, цепное правило позволяет представить производную по каждому весу в виде произведения более простых элементов (производных функции потерь и функций активации нейронов по их параметрам), которые мы уже можем рассчитать.

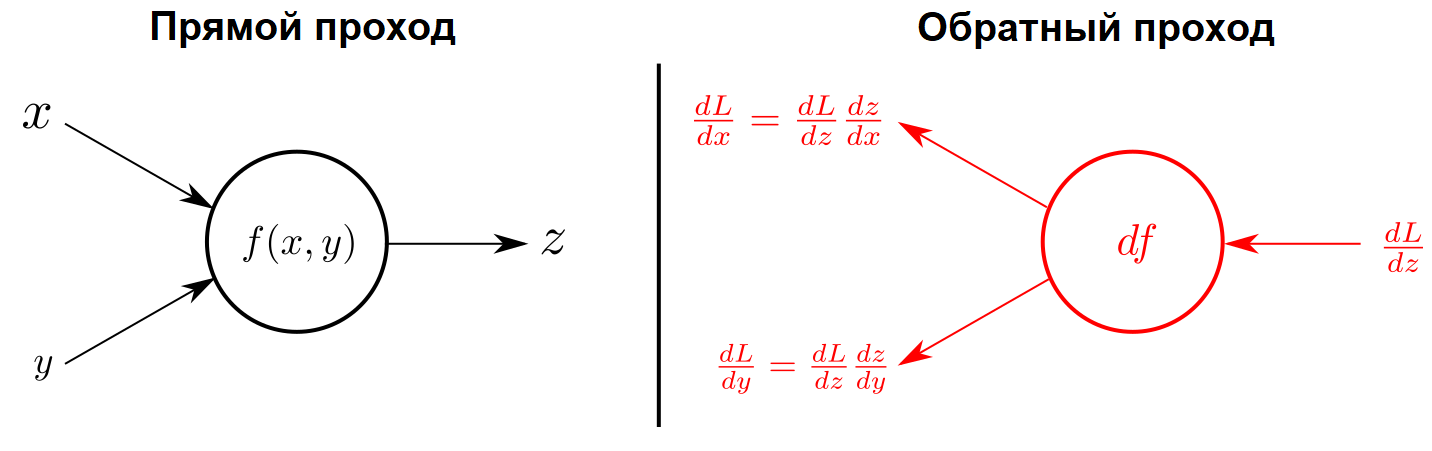
Такой метод расчета градиента называется обратным распространением ошибки, или просто обратным распространением (back-propagation). Именно этот метод дал старт широкому распространению всех видов нейронных сетей, которые изменили мир. История искусственных нейронных сетей началась еще в 1960-х, но лишь недавно появились вычислительные мощности, позволяющие реализовать обратное распространение.

Плотность распределения вероятности

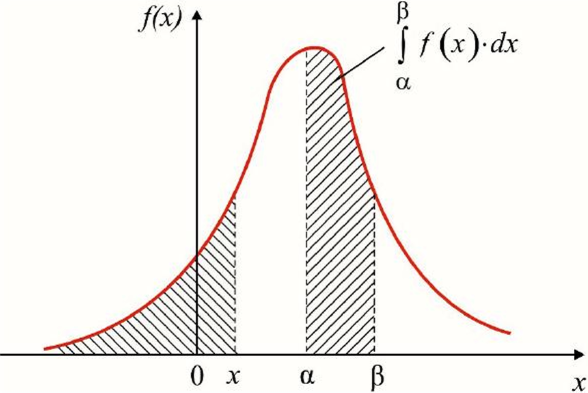
Одно из самых очевидных применений интегралов в машинном обучении – это интегрирование функции плотности распределения вероятности, занимающей центральное место в статистике. Вероятность того, что случайная величина находится в интервале между alpha и beta, равна определенному интегралу по функции плотности вероятности с этими пределами.

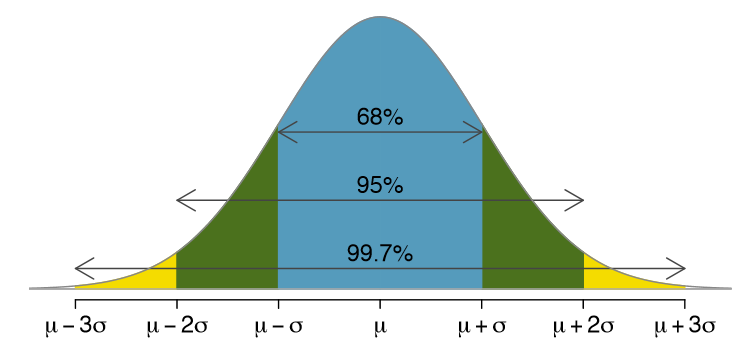
Именно из этой формулы следует знаменитое правило трех сигм – эмпирическое правило, согласно которому 68% значений нормально распределенной случайной величины находятся в пределах одного стандартного отклонения от среднего значения, 95% значений – в пределах двух отклонений, и 99.7% (почти все) – в пределах трех отклонений.

Заключение

Мы привели лишь несколько самых очевидных примеров применения математического анализа в машинном обучении. Менее очевидные встречаются буквально везде! Например, при выборе функции активации слоя нейронов надо учитывать опасность взрывных/исчезающих градиентов, то есть уметь анализировать поведение этой функции.

«Прикладное машинное обучение», в основном, это конструирование признаков.

Конструирование признаков (feature engineering) – это искусство создания нужных признаков на основе исследовательского анализа данных (exploratory data analysis, EDA). Например, анализ данных может показать квадратичную зависимость целевой переменной от некоторого признака – то есть, можно ввести признак, равный квадратному корню исходного, от которого целевая переменная будет зависеть линейно. Чтобы хотя бы заметить эту квадратичную зависимость, а тем более доказать ее, нужно очень хорошо знать математический анализ.

Поэтому самым правильным ответом на вопрос "для чего в машинном обучении нужен математический анализ", будет "для всего". Нет ни одной области машинного обучения (и науки о данных вообще), в которой он бы не применялся.

В следующих статьях мы рассмотрим самые популярные приложения линейной алгебры и теории вероятностей в машинном обучении и науке о данных.

Если вы хотите наработать необходимую для изучения Data Science математическую базу, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.