В предыдущей статье речь шла о математическом анализе. Продолжая серию публикаций к запуску авторского «Онлайн-курса по математике в Data Science Lite», поговорим о применении линейной алгебры в машинном обучении (завершит цикл статья о теории вероятностей и статистике – прим. ред.). За примерами далеко ходить не нужно: напротив, очень трудно найти такую сферу машинного обучения, в которой не используется линейная алгебра. Причем не только ее основные методы, вроде операций с векторами и матрицами, но и продвинутые вроде сингулярного разложения матрицы (Singular Value Decomposition, SVD), метода главных компонент (Principal Component Analysis, PCA) и метода опорных векторов (Support Vector Machines, SVM). Последний – один из основных алгоритмов машинного обучения.
Далеко не каждый курс линейной алгебры, даже на математических факультетах, рассматривает все ее приложения в машинном обучении. (То же самое можно сказать и о статистике, которая также является одной из основ Data Science и машинного обучения). Это обусловливает необходимость специальных курсов математики для Data Science.
Основы
Линейная алгебра работает с векторами и матрицами – а точнее, с их линейными комбинациями, также являющимися векторами и матрицами. Математически вектор можно представить набором действительных чисел:
Такой набор может представлять очень разные сущности: например, геометрический вектор в некоторой системе координат (при этом числа ai умножаются на векторы базиса), полином (числа ai умножаются на xi) и вообще любую линейную комбинацию каких-либо элементов. Матрица – это такой же набор действительных чисел, но организованный в виде прямоугольника. Матрицу тоже можно представить в виде длинного вектора, если поставить ее столбцы друг на друга.
Что в машинном обучении можно представить в виде векторов и матриц? Практически всё! Например, одна строка из набора данных – это вектор, каждый элемент которого представляет значение некоторого признака. Весь тренировочный набор данных (или, в случае нейронной сети, один batch из этого набора) – это матрица. Изображение, которое будет распознавать сверточная нейронная сеть – тоже матрица чисел, соответствующих отдельным пикселям. Градиент функции потерь – это вектор, и так далее.
Произведение векторов, умножение матрицы на вектор и произведение матриц – все это используется в машинном обучении. Например, модель линейной регрессии с вектором весов w и вектором признаков x можно записать в виде произведения векторов, если добавить в вектор признаков x[0] = 1:
Поскольку результат линейной регрессии – произведение векторов, произведение матрицы тренировочного набора данных на вектор весов дает вектор предсказаний модели. Если вычесть из него вектор истинных значений, получится вектор ошибок, который можно передать в функцию потерь.
В качестве примера перемножения матриц представим, что у нас есть набор изображений для обучения сверточной нейронной сети, и мы хотим дополнить этот набор поворотами этих изображений, чтобы сеть могла распознавать изображения независимо от их наклона. Поворот изображения – это частный случай умножения матрицы векторов координат на матрицу трансформации, которую также изучает линейная алгебра. Матрица трансформации для поворота координат на угол theta выглядит так:
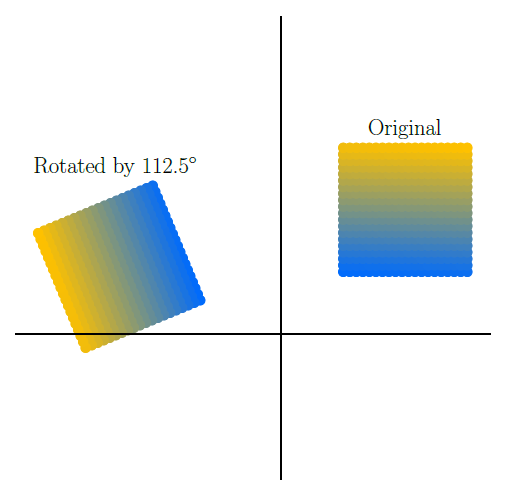
Измерения
Норма вектора – это термин линейной алгебры, определяющий длину вектора и расстояние между векторами (как длину разности между ними). Существуют нормы различных порядков, но обычно используются только первые два:
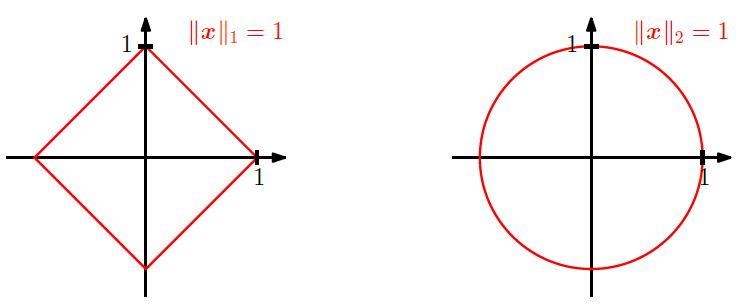
Норма L2(x-y) – это расстояние между векторами x и y. Обе нормы используются в машинном обучении для регуляризации функции потерь: лассо-регуляризация использует L1, регуляризация Тихонова – L2, а эластичная сеть – и ту, и другую.
Косинус угла между двумя векторами x и y линейная алгебра определяет так:
Эта формула – самый популярный метод оценки сходства двух векторов. Если косинус угла близок к единице, то угол между векторами минимален, то есть векторы направлены почти одинаково. Если он близок к минус единице, векторы направлены почти противоположно. Наконец, если косинус близок к нулю, то векторы перпендикулярны (ортогональны), то есть, совершенно не зависят друг от друга.
Измерение меры сходства используется в машинном обучении очень широко – например, рекомендательные системы часто измеряют сходство векторов пользователей по их предпочтениям, и на основании этого сходства принимается решение, что похожим пользователям можно рекомендовать продукты, которые уже понравились одному из них.
Разумеется, оценка сходства широко применяется и в моделях кластеризации – например, метод k-Nearest Neighbors размечает кластеры именно по степени сходства элементов друг с другом.
Сингулярное разложение матриц (SVD)
Квадратная матрица называется ортогональной, если все ее столбцы ортонормальны – норма каждого из них равна единице, и все они попарно ортогональны, то есть образуют ортонормальный базис. Ортогональные матрицы обладают следующими свойствами:
Сингулярное разложение матрицы вводится следующей теоремой линейной алгебры: любую невырожденную прямоугольную матрицу Am*n можно представить в виде произведения трех матриц Um*m, Em*n и Vn*n, где U и V – ортогональные матрицы, а E – прямоугольная матрица, в которой все элементы, кроме диагональных, равны нулю.
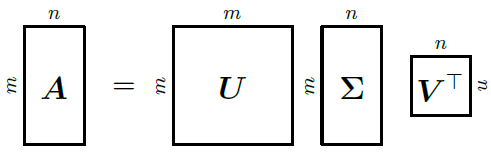
Сингулярное разложение широко используется в рекомендательных системах. Оно позволяет найти базисы пространства строк и пространства столбцов, то есть элементарные признаки обоих пространств. Например, если строки матрицы соответствуют читателям, столбцы – книгам, а сама матрица содержит оценки, которые пользователи поставили книгам, то сингулярное разложение матрицы выделит "типичных читателей" и "типичные книги". Каждого реального читателя и каждую реальную книгу можно представить линейной комбинацией "типичных", после чего будет достаточно легко рассчитать ожидаемую оценку любой книги любым читателем.
Методов, позволяющих современным компьютерам обрабатывать огромные разреженные матрицы пользовательских оценок за приемлемое время, очень мало, так что сингулярное разложение матриц применяется очень широко.
Метод главных компонент (PCA)
Метод главных компонент – один из основных методов сокращения размерности данных, используемых в машинном обучении. Сокращение размерности применяется как при анализе данных, чтобы найти наиболее важные переменные и сконструировать новые признаки на их основе, так и при моделировании, если количество признаков очень велико, и большинство из них слабо влияют на результат. Метод главных компонент находит такую проекцию данных на пространство меньшей размерности, которая максимально сохраняет дисперсию данных.
Продемонстрируем работу метода главных компонент на примере двухмерного набора данных, который мы будем проецировать на одномерное подпространство (линию). Метод состоит из нескольких шагов:
- Вычитаем среднее значение, чтобы набор данных имел среднее значение 0. Это сокращает риск возникновения числовых проблем.
- Стандартизируем. Делим элементы данных на стандартное отклонение sigmad по каждому измерению d. Теперь данные не имеют единиц измерения, а их дисперсия по каждой оси равна 1, что отмечено на рис. в) голубыми стрелками.
- Выполняем спектральное разложение матрицы ковариации. Вычисляем матрицу ковариации данных, ее собственные векторы и собственные значения. На рис. г) собственные векторы масштабированы соответствующими собственными значениями (голубые стрелки), и более длинный вектор соответствует подпространству главных компонент. Матрица ковариации данных изображена в виде эллипса.
- Проецируем данные в подпространство. Рисунок е) показывает итоговую проекцию, перенесенную в исходное пространство данных.
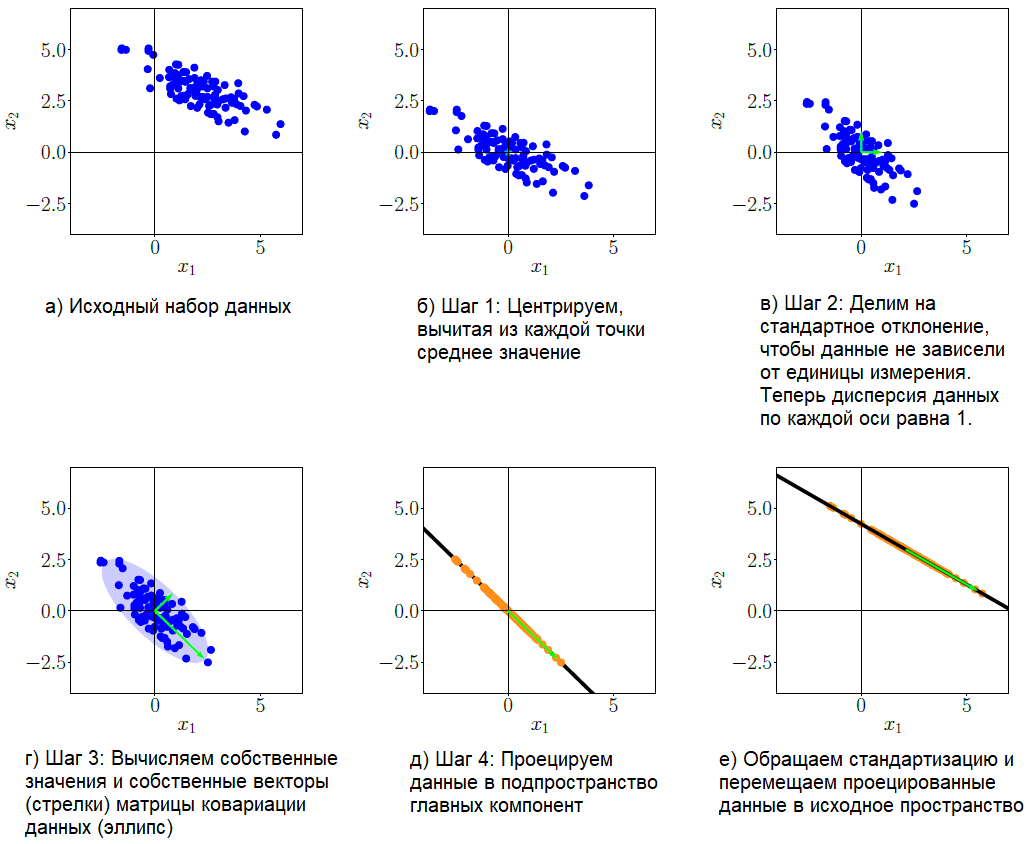
Из описания метода главных компонент видно, что в нем используются понятия не только линейной алгебры, но и статистики (среднее значение, дисперсия, отклонение, матрица ковариации). Тем не менее, основные операции выполняются методами линейной алгебры, ведь именно она описывает проекции из одного пространства в другое, собственные векторы и собственные значения, а также спектральное разложение матриц.
Метод опорных векторов (SVM)
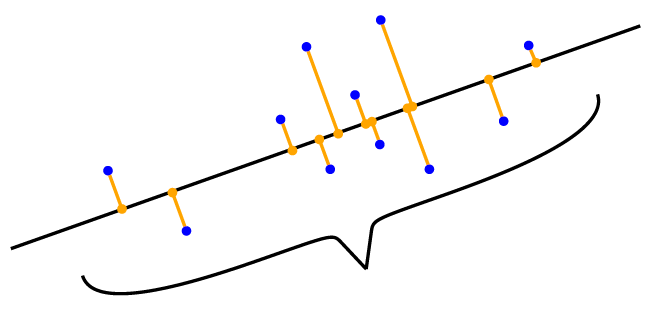
Один из основных методов построения моделей машинного обучения – это метод опорных векторов (Support Vector Machine). Этот метод основан на построении гиперплоскости, максимально разделяющей объекты разных классов – то есть, обеспечивающей максимальное расстояние между граничными точками. Мы не будем вдаваться в детали его реализации, поскольку они достаточно сложны и выходят за рамки нашей статьи. Метод очень подробно, с примерами кода и анимацией, описан в статье на Хабре, откуда взята следующая иллюстрация:
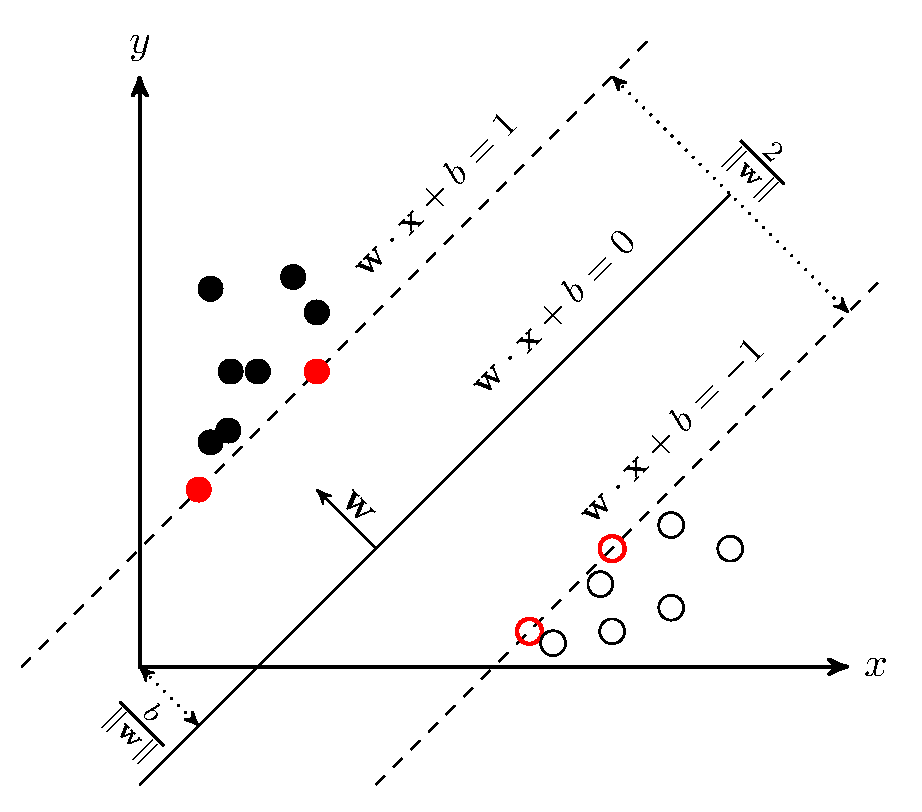
Метод опорных векторов широко используется для задач бинарной классификации, а также сегментации изображений и многих других задач. Существует множество различных вариаций этого метода, причем он позволяет задать спрямляющее ядро, при правильном выборе которого результирующая модель зачастую оказывается более точной, чем модели на основе нейронных сетей – однако это ядро невозможно подобрать автоматически, так что его выбор представляет собой искусство Data Scientist'а. Метод хорошо работает с данными небольшого объема и с данными, имеющими большое количество признаков.
Для нас главное – то, что векторы и гиперплоскости относятся к линейной алгебре, как и весь метод в целом, и для его успешного применения, а также для правильной интерпретации его результатов, хорошее знание линейной алгебры просто необходимо.
Заключение
Мы рассмотрели только самые важные и очевидные приложения линейной алгебры в машинном обучении, но из приведенных примеров понятно, насколько широко она применяется, и насколько глубоко требуется ее знать для уверенного понимания хотя бы основных методов. Разумеется, для реальной работы в области машинного обучения придется изучить намного больше, чем описано в этой статье (предыдущая публикация была посвящена приложениям математического анализа, а в следующей речь пойдет о теории вероятностей и статистике – прим. ред.).
Надеюсь, что вы по-настоящему любите математику, или, по крайней мере, она вас не пугает.
Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.




Комментарии