С одной стороны, роль теории вероятностей и статистики в машинном обучении сравнительно невелика: используются лишь базовые понятия, хотя и довольно широко. С другой стороны, разведочный анализ данных, их очистка, подготовка и конструирование новых признаков – это чистая статистика. А поскольку эти операции в прикладной науке о данных (Data Science) занимают 90-95% времени, самый важный раздел математики для Data Scientist'ов – именно статистика. Кстати, это отлично демонстрирует разницу между машинным обучением и наукой о данных.
"Вероятности" классификации
Практически все модели классификации, используемые в машинном обучении, на самом деле выдают не единственную метку класса (или его номер), а набор "вероятностей" принадлежности к каждому классу. Логистическая регрессия с бинарной классификацией – это та же линейная регрессия, результат которой пропускается через функцию сигмоиды, преобразующую весь диапазон действительных чисел к диапазону [0,1].
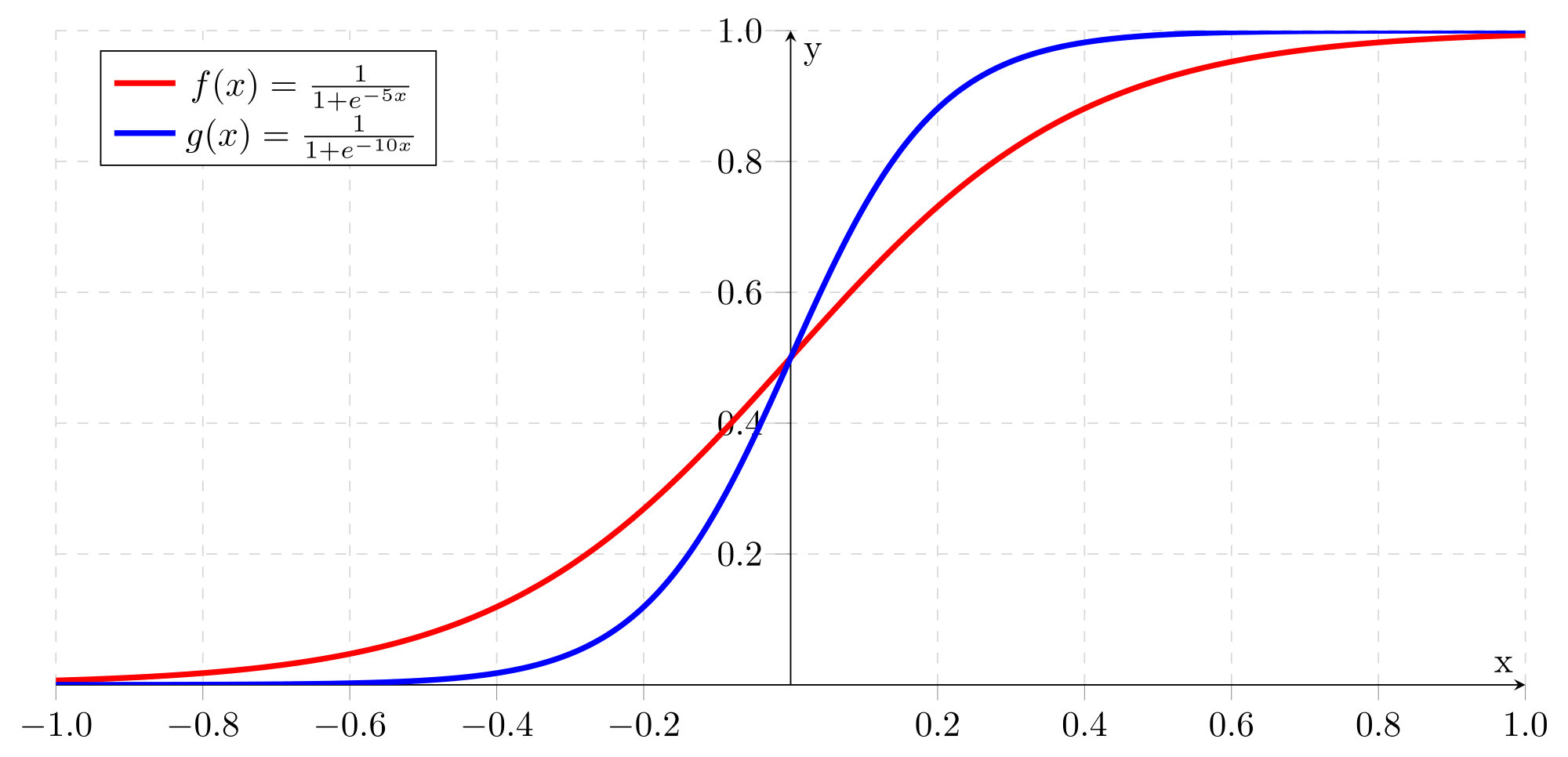
Число p, являющееся результатом сигмоиды, считается "вероятностью" принадлежности результата к одному из классов, а "вероятность" принадлежности к другому классу равна 1-p. Разумеется, это не настоящие вероятности – строго говоря, в данном случае вообще нет смысла говорить о вероятности, ведь результат классификации однозначен. Возможно, в данном случае было бы правильнее называть результат степенью уверенности: например, модель считает, что данный экземпляр принадлежит к классу 1 с уверенностью 74%. Тем не менее, принято называть этот показатель именно вероятностью.
Если классов больше двух, вместо сигмоиды используется Softmax – функция, преобразующая вектор вещественных чисел z размерности N в вектор неотрицательных чисел той же размерности, сумма которых равна 1 (sigma):
В результате мы получаем "вероятности" принадлежности к каждому классу, которые можно интерпретировать по-разному. Традиционно результатом классификации считается класс с максимальной "вероятностью", но ничто не мешает принять какие-то особые меры в тех случаях, когда модель "не уверена" в результате – например, если разница между двумя максимальными "вероятностями" невелика.
Если для классификации используется нейронная сеть, и классов больше двух, последним слоем этой сети практически всегда будет слой Softmax.
Все будет нормально
Нормальное распределение, или распределение Гаусса – это семейство функций плотности распределения вероятности с двумя параметрами: mu (среднее значение, оно же медиана и мода) и sigma (стандартное или среднеквадратическое отклонение). Иногда вместо sigma используется параметр sigma2 – дисперсия нормального распределения:
График функции плотности нормального распределения похож на колокол. Его центральная координата равна mu, а стандартное отклонение sigma определяет уровень "крутизны" графика: чем оно меньше, чем большая доля значений переменной будет находиться недалеко от центра.
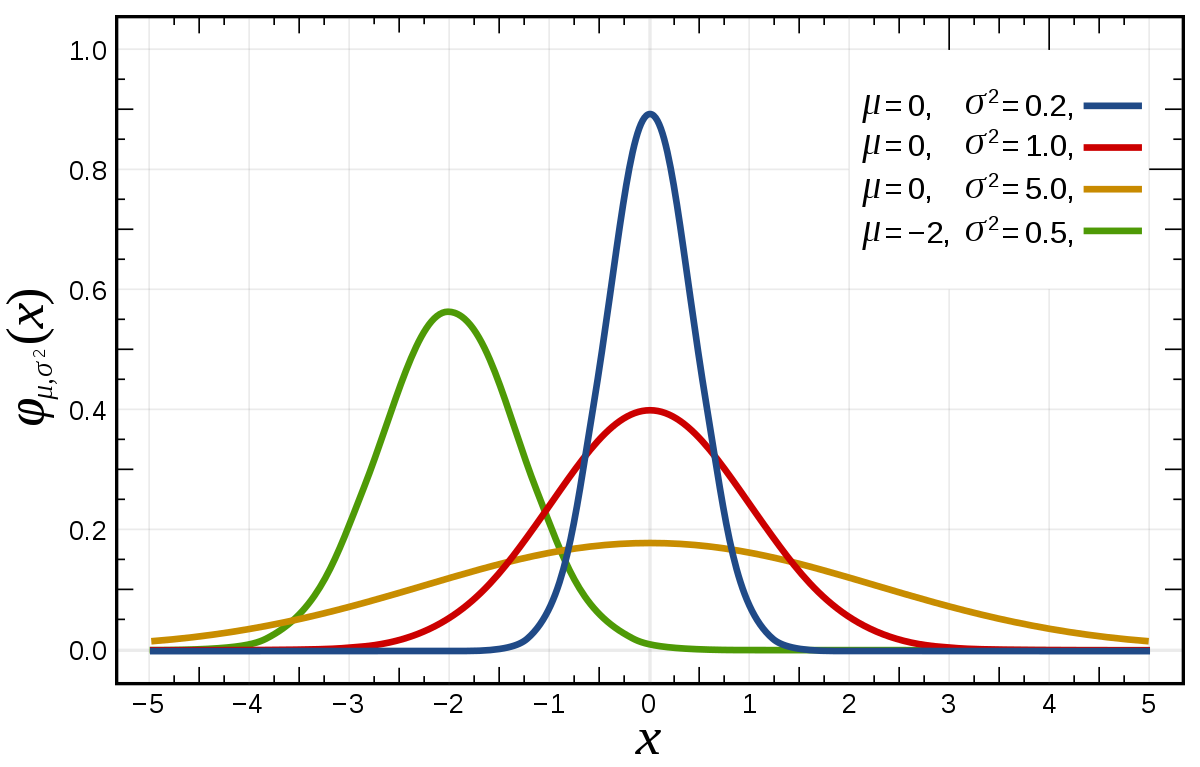
Центральная предельная теорема гласит, что сумма многих слабо зависимых друг от друга случайных величин имеет нормальное распределение – именно поэтому оно имеет огромное значение для статистики, которая обычно анализирует массовые явления. Например, если каждый человек, проходящий мимо кофейни, заходит выпить кофе с определенной вероятностью – то количество посетителей кафе будет иметь нормальное распределение.
Нормальное распределение настолько важно, что многие методы машинного обучения работают намного лучше, если данные нормально распределены (или даже вообще не работают в противном случае). Поэтому нормализация данных – очень часто выполняемая операция, а для нейронных сетей даже разработан слой пакетной нормализации (batch normalization).
Байесовские модели
Одно семейство методов машинного обучения полностью основано на теории вероятностей – байесовские модели. Теорема Байеса определяет вероятность события A, при условии события B, через обратную вероятность и вероятности A и B:
Вероятностные модели предполагают, что данные, на которых они обучаются, отражают реальное распределение вероятностей появления всех значений каждого признака. Если данных достаточно много, и все признаки распределены нормально, это предположение может быть почти верным. Например, в задаче классификации вероятность соответствия результата y для набора признаков x1, x2,..., xn одному из классов A предсказывается по обобщенной теореме Байеса:
Таким образом, для получения вероятности того, что результат y при значениях признаков x1, x2,..., xn примет значение А, нужно рассчитать три вероятности:
- P(y = A) – заведомо известная вероятность того, что у равна A.
- P(x1, x2,..., xn) – совместная вероятность того, что признаки примут такие значения (легко рассчитывается по набору данных или с помощью теоремы о полной вероятности).
- P(x1, x2,..., xn | у = A) – условная вероятность того, что признаки примут такие значения при данном значении результата (рассчитывается по набору данных либо с помощью цепного правила вероятностей).
Наиболее популярен наивный байесовский классификатор, который предполагает, что признаки совершенно не зависят друг от друга. Возможно, такое предположение и впрямь наивно, зато оно очень упрощает расчет условной вероятности.
Разведочный анализ данных
Разведочный анализ данных (exploratory data analysis, EDA) – это изучение данных для принятия решений по поводу их применения, очистки, преобразования и конструирования новых признаков. Как сказано выше, EDA – это чистая статистика, и основные цели его первого этапа – понять вид распределения признаков, основные параметры этого распределения, обнаружить выбросы и т.д.
В первую очередь для анализа данных обычно применяются гистограммы и "ящики с усами". Гистограмма просто разбивает весь диапазон данных на несколько отрезков, и для каждого отрезка выводит количество элементов набора данных, попадающих в этот отрезок. Легко заметить, что гистограмма отдаленно похожа на график функции плотности распределения вероятности, так что по ней очень легко определить, распределен ли признак нормально или имеет какое-то иное распределение. Обычно выводятся гистограммы сразу для нескольких признаков.
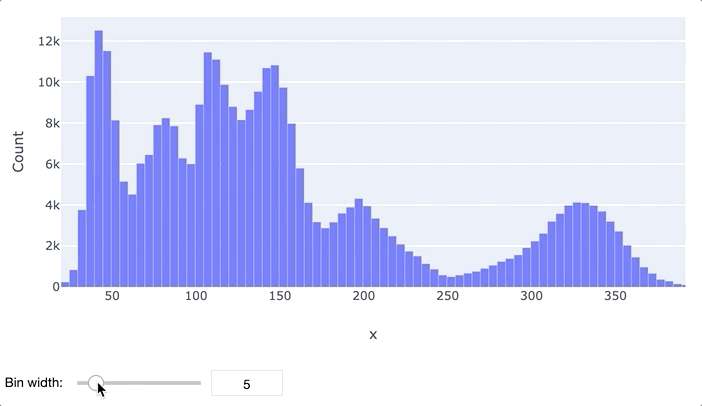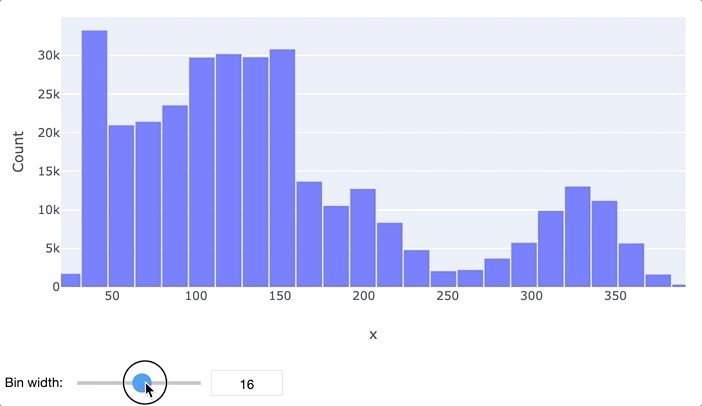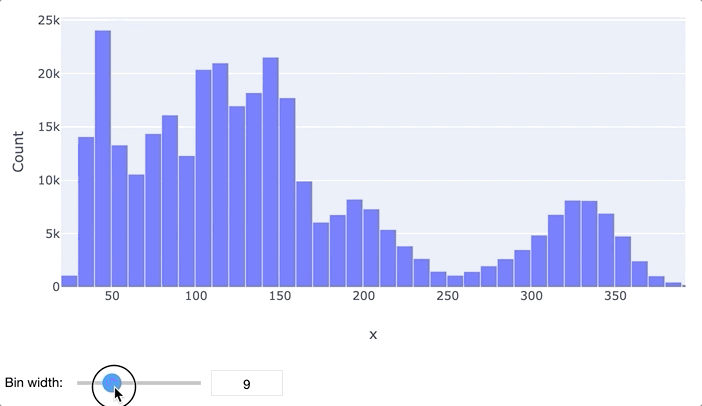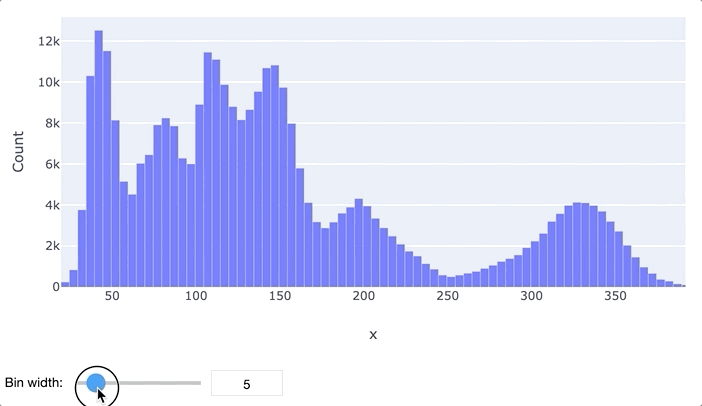
"Ящик с усами" не позволяет увидеть общую картину распределения, зато предоставляет ценную информацию о его параметрах, особенно квантилях. Квантиль – это такое значение признака, что заданный процент значений этого признака в наборе данных меньше этого квантиля. Например, квантиль 50% – это такое значение, что половина значений признака меньше, а вторая половина – больше него, этот квантиль называется медианой. Квантили 0%, 25%, 50%, 75% и 100% называются квартилями, поскольку они делят область определения признака на четыре части.
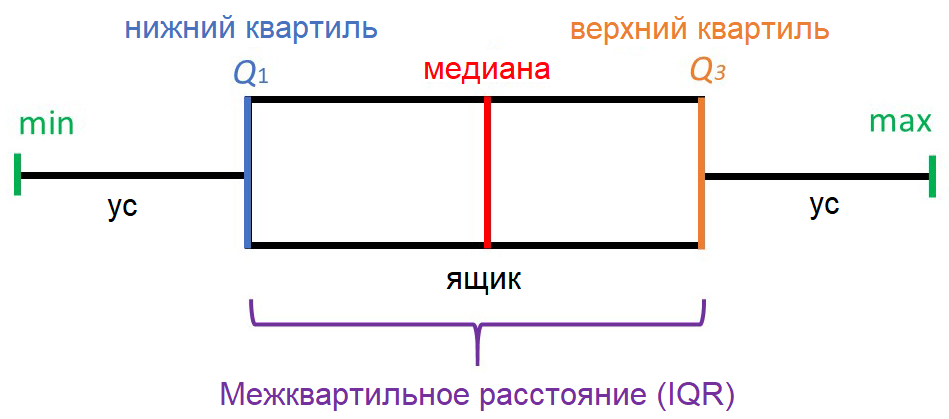
"Усы" выводятся без учета выбросов (outliers) – значений, больших Q3+1.5*IQR или меньших Q1-1.5*IQR. Принято считать, что выбросы скорее свидетельствуют об ошибках ввода данных, чем о реальных значениях признаков, и с ними надо что-то делать – например, удалить. На нашем рисунке выбросы не показаны, а в реальных "ящиках с усами" они выводятся в виде кружков за пределами "усов". Все понятия, о которых мы говорили, изучает статистика.
Анализ зависимостей между признаками
Для исследования возможных зависимостей между признаками используется множество методов, но самые простые из них – попарная диаграмма и матрица корреляции. Начнем с попарной диаграммы (pairplot). Выбираются несколько признаков, зависимости между которыми вы хотите исследовать, и получается комбинированная диаграмма, включающая небольшую диаграмму рассеяния (scatter plot) для каждой пары параметров. В диагональных клетках обычно выводятся графики или гистограммы соответствующих признаков.
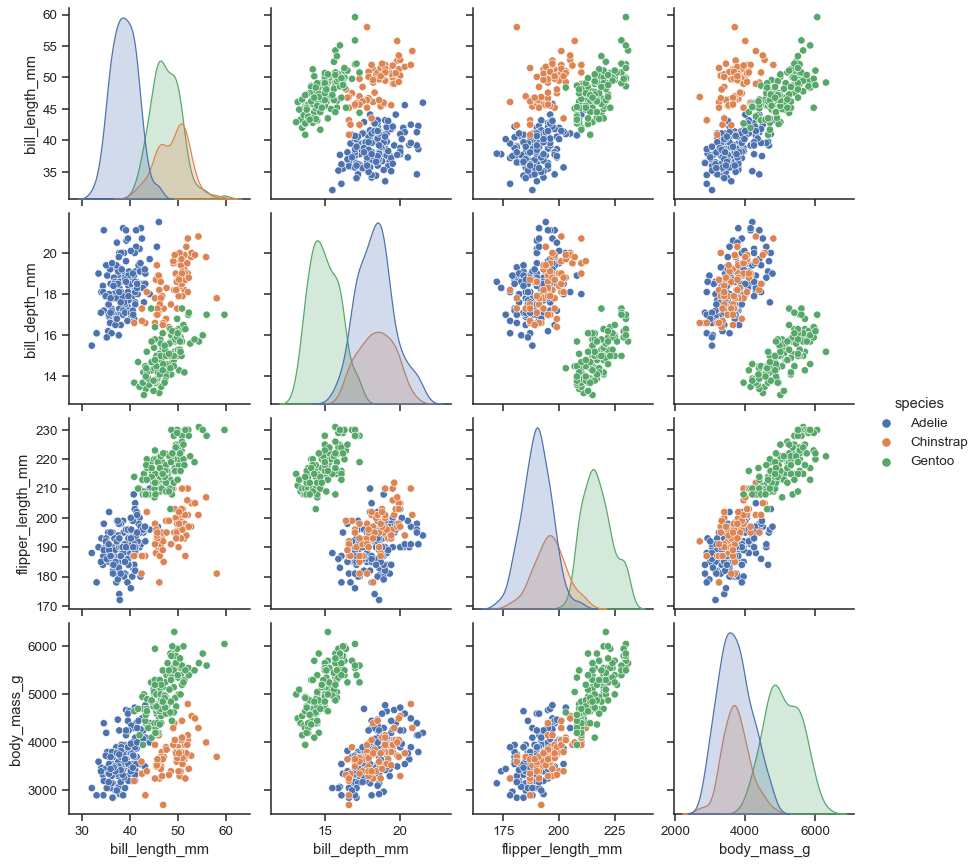
Коэффициент корреляции между двумя признаками x и y по набору данных, состоящему из n записей, считается следующим образом ("x с крышкой" и "y с крышкой" – средние значения x и y):
Коэффициент корреляции всегда находится в интервале [-1, 1], и его значение показывает, насколько велика линейная зависимость между признаками. Если его значение близко к 1, то зависимость очень сильна, если к -1, то признаки противоположны друг другу, а если к 0 – совершенно не зависят друг от друга. Для анализа многих признаков сразу обычно выводится матрица корреляции, в которой цвет каждого коэффициента соответствует его значению.
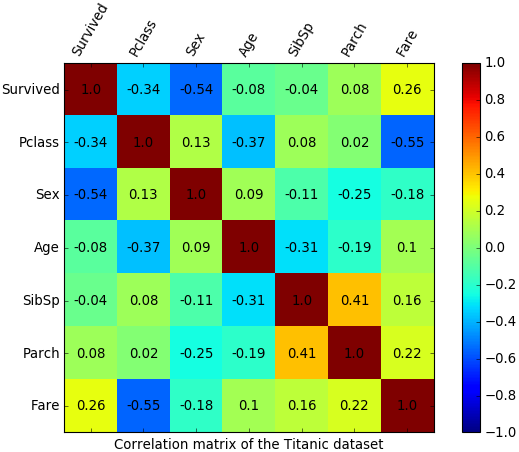
Например, из матрицы корреляции для набора данных о "Титанике" легко увидеть, что какая-то положительная корреляция есть только между количеством родителей и количеством детей на борту: люди плыли либо парами/в одиночку, либо целыми семьями. Отрицательная корреляция есть между пассажирским классом и ценой проезда (естественно, билеты низших по номеру классов стоили дороже) и между полом и признаком выжившего: мужчины уступали места в шлюпках дамам.
Заключение
Как мы уже говорили, статистика занимает особое место в науке о данных, поскольку все данные собираются и обрабатываются именно методами статистики. Более того, иногда вся работа Data Scientist'а, включая создание и усовершенствование моделей, проводится только для того, чтобы доказать или опровергнуть какую-нибудь статистическую гипотезу! А это значит, что каждый Data Scientist обязан знать статистику на профессиональном уровне – по крайней мере, именно такие требования к ним предъявляют на Западе. Помимо статистики придется освоить основы математического анализа и линейной алгебры, о которых шла речь в первых публикациях нашего небольшого цикла.
Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.




Комментарии