Динамическое программирование или подход «разделяй и властвуй»? В этой статье рассматриваем сходства и различия двух способов.
В качестве примеров будут рассмотрены алгоритмы бинарного поиска и вычисления минимальной дистанции редактирования (расстояние Левенштейна).
В чём вопрос
При изучении алгоритмов многие сталкиваются с трудностями в понимании идеи динамического программирования и отличий динамического подхода (dynamic programming, DP) от подхода «разделяй и властвуй» (divide-and-conquer, DC). Обычно при сравнении этих двух парадигм приводятся в пример соответствующие тому и другому подходу алгоритмы вычисления чисел Фибоначчи. Но пытаясь продемонстрировать обе парадигмы на одном и том же примере, мы можем упустить из виду важную деталь. Она заключается в том, что DP и DC нужны для разных типов задач.
Сходство DP и DC
Обе парадигмы похожи тем, что работают путем рекурсивного разбиения задачи на две или более подзадач того же или похожего типа. Разбиение продолжается, пока подзадачи не станут настолько простыми, чтобы их можно было решить напрямую, а затем их решения объединяются для получения ответа.
Динамическое программирование позволяет оптимизировать задачу «разделяй и властвуй». В то же время важно заметить, что подход динамического программирования не универсален: он может быть использован только в том случае, если задача удовлетворяет определенным ограничениям.
Ограничения на задачу для DP
Существует два ключевых ограничения, которые должны выполняться у задачи «разделяй и властвуй», чтобы для ее решения можно было использовать динамическое программирование:
- Оптимальная подструктура – оптимальное решение задачи может быть построено из оптимальных решений ее подзадач.
- Перекрывающиеся подзадачи – задача может быть разбита на подзадачи, которые повторно используются несколько раз, или рекурсивный алгоритм решения решает одну и ту же подзадачу снова и снова, не всегда создавая новые подзадачи.
Если эти два условия выполнены, задача может быть оптимизирована с использованием динамического программирования.
Как работает динамическое программирование
Динамическое программирование дополняет «разделяй и властвуй» с помощью техник, известных как мемоизация и табуляция. Смысл обеих заключаются в кэшировании решений перекрывающихся подзадач для того, чтобы повторно их использовать, не пересчитывая заново. Такой подход может существенно повысить производительность за счет использования большего количества памяти на кэш. Например, простая рекурсивная реализация функции Фибоначчи (функции, вычисляющей n-ное число Фибоначчи) имеет экспоненциальную временную сложность, а решение динамическим программированием справляется с задачей за линейное время.
Мемоизация (memoization, заполнение кэша сверху вниз) заключается в кэшировании и повторном использовании ранее вычисленных результатов. Так, memoized fib будет выглядеть следующим образом:
memFib(n) {
if (mem[n] is undefined)
if (n < 2) result = n
else result = memFib(n-2) + memFib(n-1)
mem[n] = result
return mem[n]
}
Табуляция (tabulation, заполнение кэша снизу-вверх) похожа на мемоизацию, но фокусируется на заполнении кэша. Вычисление значений в кэше выполняется итеративно. Так будет выглядеть соответствующая версия функции fib:
tabFib(n) {
mem[0] = 0
mem[1] = 1
for i = 2...n
mem[i] = mem[i-2] + mem[i-1]
return mem[n]
}
Больше о мемоизации и табуляции, а также их сравнительном анализе можно почитать здесь.
Основная идея, которую нужно усвоить, состоит в следующем: если задача «разделяй и властвуй» имеет перекрывающиеся подзадачи, становится возможной оптимизация программы путем кэширования вычисленных решений подзадач с помощью мемоизации или табуляции.
В чем же разница между DC и DP?
Поскольку мы уже разобрались, в чем состоят требования динамического программирования к задаче, и какие существуют методологии кэширования, попробуем объединить изученное в одну общую картину.
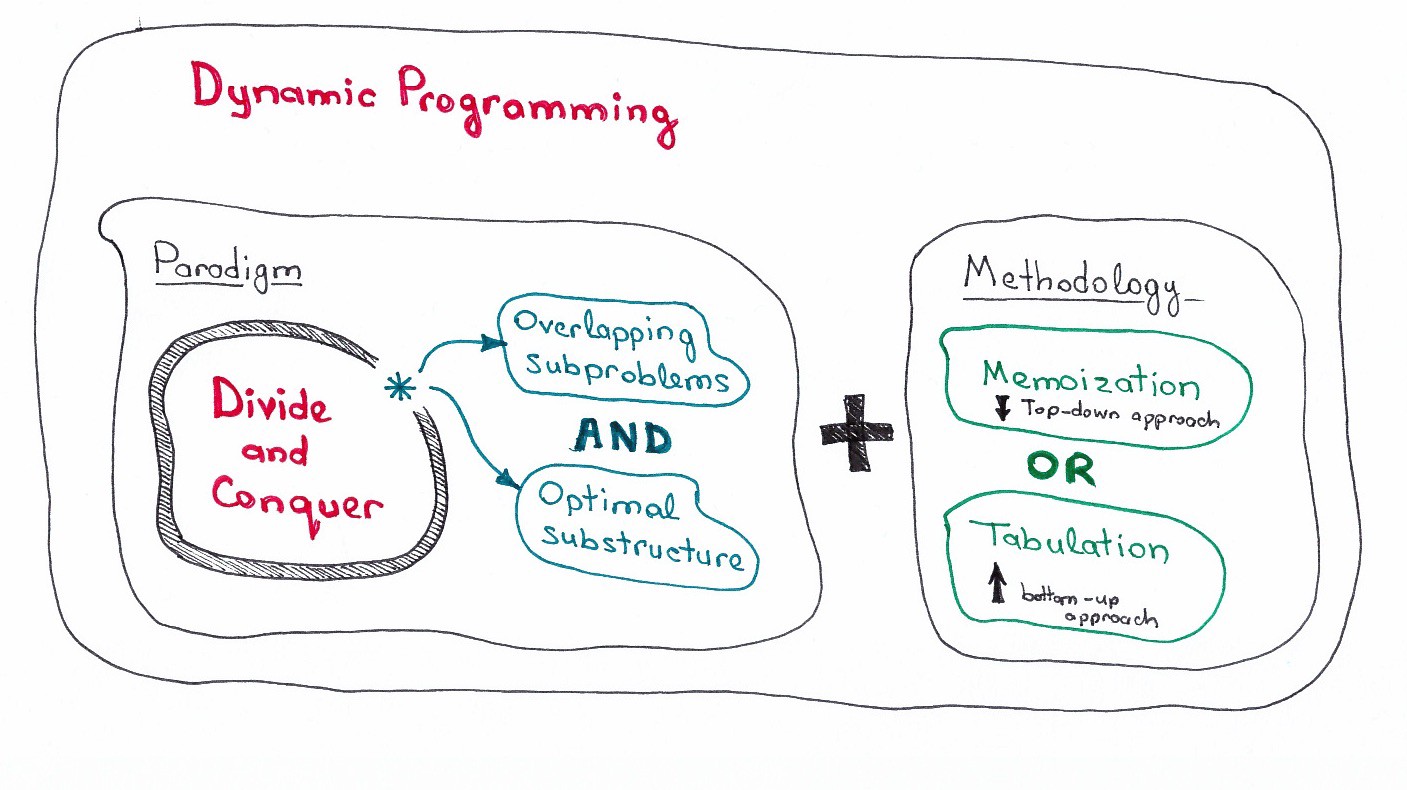
Давайте решим пару задач, используя обе парадигмы, чтобы немного прояснить иллюстрацию.
Пример DC-задачи: бинарный поиск
Алгоритм бинарного поиска представляет собой алгоритм, который находит индекс целевого значения в отсортированном массиве. Бинарный поиск сравнивает целевое значение с центральным элементом массива. Если они не равны, то искомый элемент может содержаться только в одной из половин массива. Такой вывод мы можем сделать из предположения о том, что массив отсортирован.
Если искомый элемент больше центрального, то мы продолжаем поиск в большей половине массива, а если меньше – то, соответственно, в меньшей. И так до тех пор, пока нецелевое значение не будет найдено. А если поиск заканчивается тем, что оставшаяся половина пуста, можно утверждать, что массив не содержит искомого элемента.
Пример
Ниже представлена визуализация работы алгоритма бинарного поиска, где целевым значением является 4.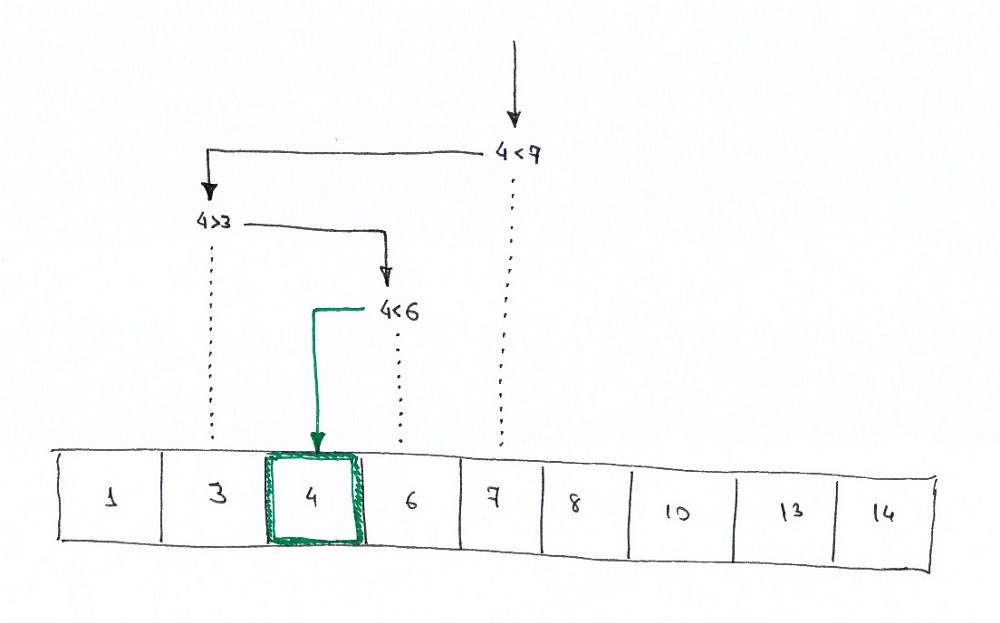
Нарисуем то же самое, но в виде дерева решений.
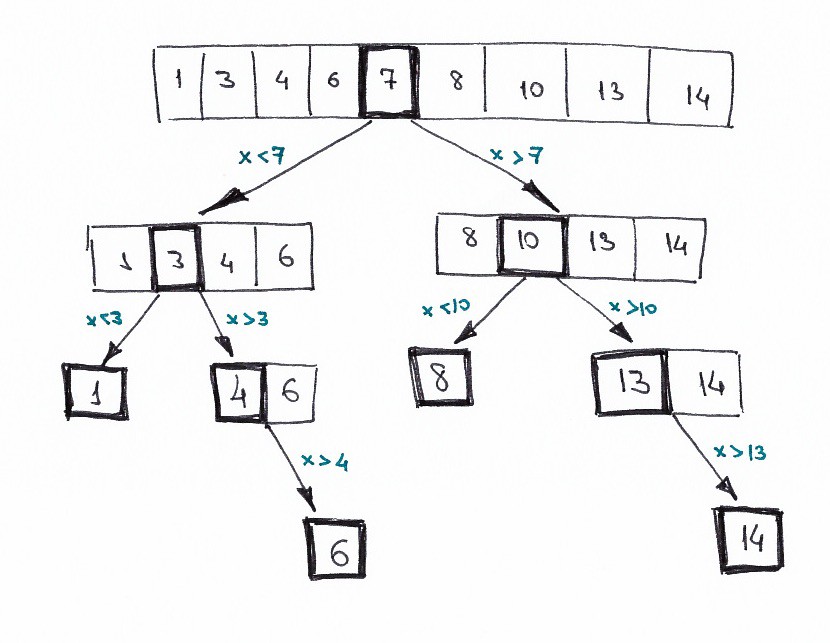
В логике бинарного поиска ясно прослеживается принцип «разделяй и властвуй». Мы итеративно делим исходный массив, каждый раз уменьшая область поиска и сводя задачу к тривиальной.
Можем ли мы задействовать динамическое программирование? Нет. Подзадачи, возникающие при дроблении массива, совершенно независимы. Они не перекрываются, а это одно из ограничений, которым должна соответствовать задача DP.
Если решая некоторую задачу, вы нарисуете дерево решений, и это действительно дерево, а не граф, значит, перекрывающихся задач нет, и динамическое программирование применить нельзя.
Немного кода
Здесь можно найти исходный код бинарного поиска с пояснениями и тестами.
function binarySearch(sortedArray, seekElement) {
let startIndex = 0;
let endIndex = sortedArray.length - 1;
while (startIndex <= endIndex) {
const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);
// Если мы нашли искомый элемент, просто возвращаем его индекс.
if (sortedArray[middleIndex] === seekElement)) {
return middleIndex;
}
// Решаем, какую половину исследовать дальше: левую или правую.
if (sortedArray[middleIndex] < seekElement)) {
// Выбираем правую половину.
startIndex = middleIndex + 1;
} else {
// Иначе, левую.
endIndex = middleIndex - 1;
}
}
return -1;
}
Пример DP-задачи: дистанция редактирования
Классической иллюстрацией задачи динамического программирования служит алгоритм нахождения числа Фибоначчи. Но мы возьмем немного более сложный алгоритм ради разнообразия. Это поможет лучше понять концепцию.
Минимальное расстояние редактирования (или расстояние Левенштейна) − это метрика для измерения разницы между двумя последовательностями символов.
Неформально расстояние Левенштейна между двумя словами определяется как минимальное количество односимвольных изменений (вставка, удаление или замена символа), необходимое для трансформации одного слова в другое.
Пример
Расстояние Левенштейна между словами «kitten» и «sitting» равно 3. Приведенная ниже последовательность односимвольных изменений меняет одно слово на другое, и, на самом деле, нет никакого способа сделать это за меньшее количество действий.
- kitten → sitten (замена «s» для «k»)
- sitten → sittin (подстановка «i» для «e»)
- sittin → sitting (вставка «g» в конце).
Приложения
Эта метрика имеет широкий спектр приложений: проверка орфографии, системы коррекции для оптического распознавания символов, поиск нечетких строк и программное обеспечение для перевода естественного языка.
Математическое определение
Математически расстояние Левенштейна между двумя строками a и b (длины |a| и |b| соответственно) задается функцией lev(|a|, |b|), определяемой следующим образом:
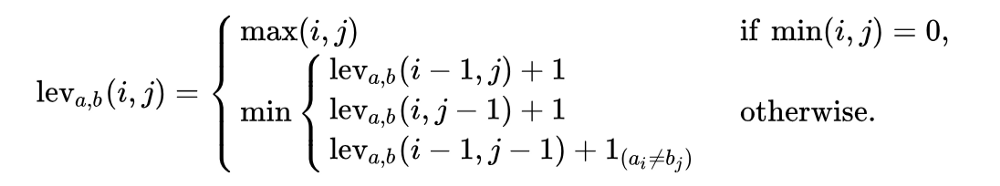
Обратите внимание, что первое выражение в min соответствует удалению (от a до b), второе − вставке, а третье − совпадению или несоответствию, в зависимости от того, являются ли соответствующие символы одинаковыми. Далее мы немного подробнее это разберем.
Пояснение
Давайте попробуем разобраться, о чем говорит данная формула. Рассмотрим простой пример: требуется найти минимальное расстояние редактирования между строками ME и MY. Интуитивно понятно, что минимальное расстояние редактирования здесь − 1 операция, и эта операция − «заменить E на Y». Но давайте попробуем формализовать интуитивные рассуждения и привести их к алгоритму, чтобы иметь возможность решать более сложные примеры, например, преобразование «Saturday» в «Sunday».
Чтобы применить формулу к преобразованию ME → MY, нам нужно знать минимальные расстояния редактирования преобразований ME → M, M → MY и M → M в предыдущем. Затем нам нужно будет выбрать минимальный и добавить +1 операцию для преобразования последних букв E → Y.
Заметен рекурсивный характер решения: минимальное расстояние редактирования трансформация вычисляется на основе трех ранее возможных преобразований. Это наталкивает на мысль о том, что алгоритм решения этой задачи следует принципу «разделяй и властвуй».
Давайте нарисуем следующую матрицу: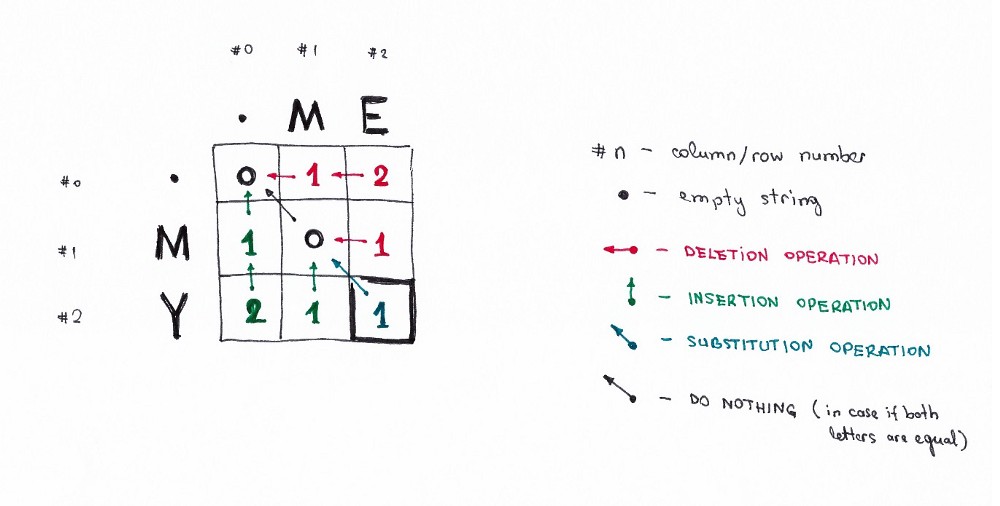
Что содержится в ячейках
(0,1): содержит красное число 1. Это означает, что нам нужна 1 операция, чтобы преобразовать M в пустую строку: <удалить M>.
(0,2): содержит красное число 2. Это означает, что нам нужно 2 операции для преобразования ME в пустую строку: <удалить E>, <удалить M>.
(1,0): содержит зеленое число 1. Нам нужна 1 операция для преобразования пустой строки в M, вставка: <вставить M>.
(2,0): содержит зеленое число 2. Это означает, что нам нужно 2 операции, чтобы преобразовать пустую строку в МY: <вставить Y>, <вставить M>.
(1,1): содержит число 0. Это означает, для преобразования M в M не требуется никаких операций.
(1,2): содержит красное число 1. Это означает, что нам нужна 1 операция для преобразования ME в M: <удалить E>.
И так далее.
Выглядит просто для такой маленькой матрицы. Но как вычислять все эти числа для больших матриц (скажем, 9x7, для Saturday → Sunday)?
Хорошая новость: согласно формуле, вам нужны только три соседние ячейки (i-1, j), (i-1, j-1) и (i, j-1) для вычисления числа для текущей ячейки (i, j). Все, что нам нужно сделать, − это найти минимум трех ячеек, а затем добавить +1 в случае, если у нас есть разные символы в строке i и столбце j.
Рекурсивный характер проблемы очевиден.
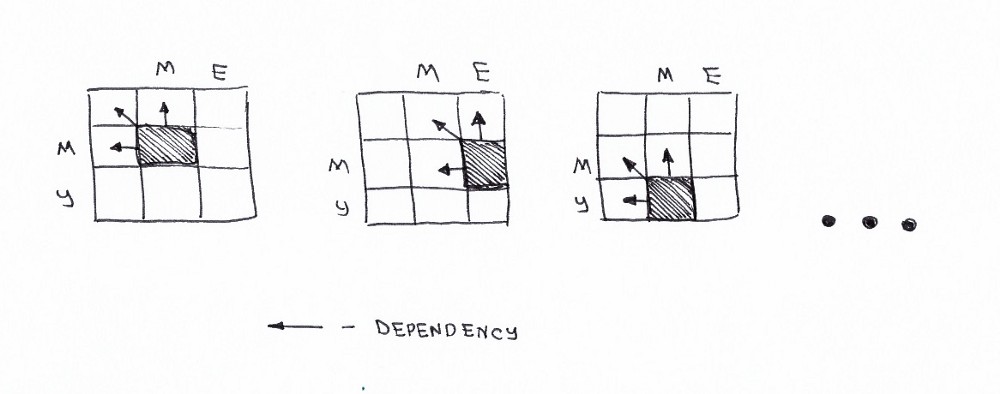
Здорово! Мы только что выяснили, что имеем дело с задачей «разделяй и властвуй». Но можем ли мы применить к ней подход динамического программирования? Удовлетворяет ли эта задача ограничениям, заключающимся в наличии перекрывающихся подзадач и оптимальной подструктуры? Да. Посмотрим на граф решений.
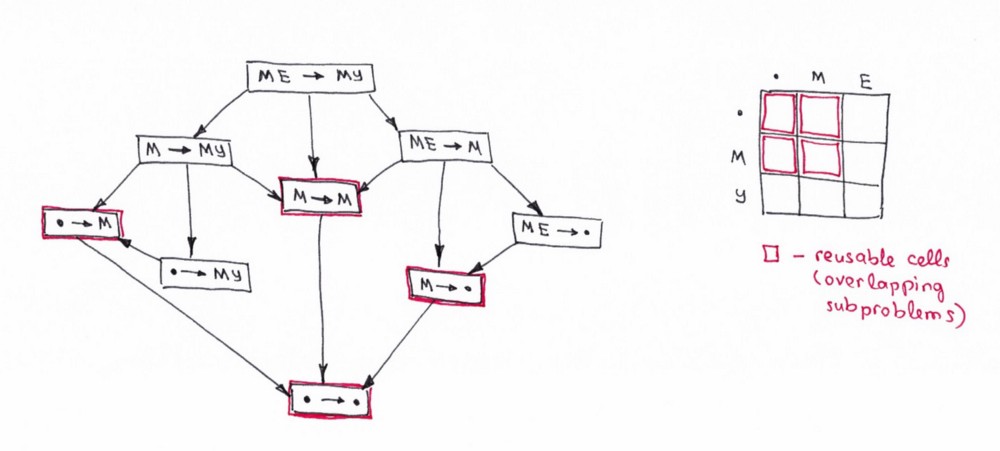
Прежде всего еще раз отметим, что это не дерево решений. Это граф. Заметны несколько перекрывающихся подзадач на изображении, отмеченных красным. Также нет способа уменьшить количество операций.
Отметим, что каждый номер ячейки в матрице вычисляется на основе предыдущих. Таким образом, здесь применяется методика табуляции (заполнение кеша снизу вверх). Вы увидите это в примере кода ниже.
Применяя эти принципы, мы можем решить более сложные случаи. Например, дистанция редактирования Saturday → Sunday.
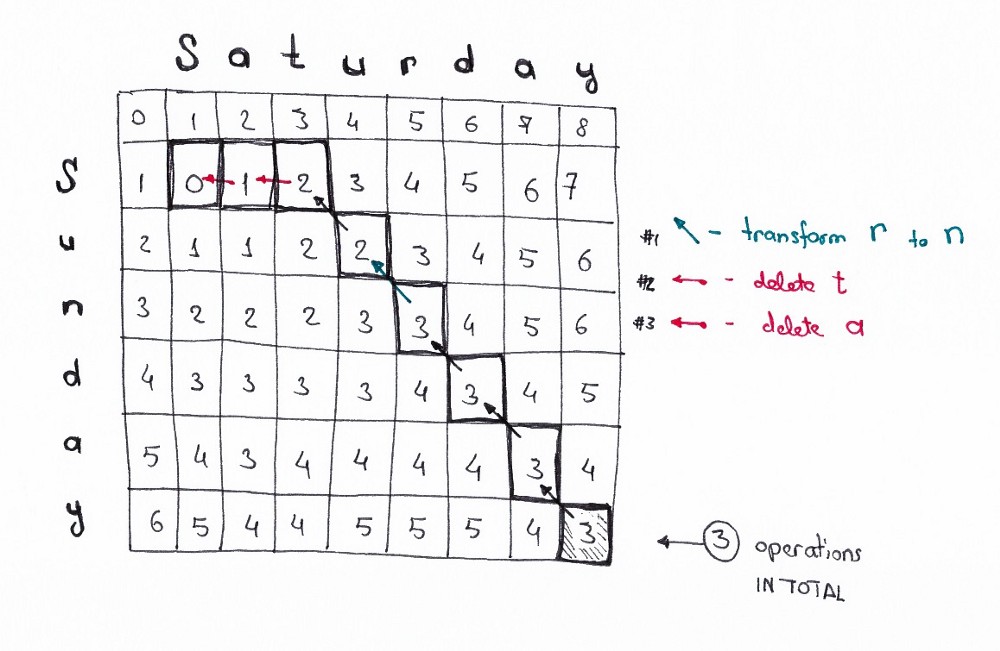
Исходный код
function levenshteinDistance(a, b) {
const distanceMatrix = Array(b.length + 1)
.fill(null)
.map(
() => Array(a.length + 1).fill(null)
);
for (let i = 0; i <= a.length; i += 1) {
distanceMatrix[0][i] = i;
}
for (let j = 0; j <= b.length; j += 1) {
distanceMatrix[j][0] = j;
}
for (let j = 1; j <= b.length; j += 1) {
for (let i = 1; i <= a.length; i += 1) {
const indicator = a[i - 1] === b[j - 1] ? 0 : 1;
distanceMatrix[j][i] = Math.min(
distanceMatrix[j][i - 1] + 1, // удаление
distanceMatrix[j - 1][i] + 1, // вставка
distanceMatrix[j - 1][i - 1] + indicator, // замена
);
}
}
return distanceMatrix[b.length][a.length];
}
Заключение
В этой статье мы сравнили два алгоритмических подхода: динамическое программирование и «разделяй и властвуй». Мы выяснили, что динамическое программирование основано на «разделяй и властвуй» и может применяться только в том случае, если проблема имеет перекрывающиеся подзадачи и оптимальную подструктуру (метрика Левенштейна послужила прекрасной тому иллюстрацией). Алгоритм решения задачи динамического программирования использует мемоизацию или табуляцию для хранения решений перекрывающихся подзадач для последующего использования.
Больше примеров задач «разделяй и властвуй» и динамического программирования с пояснениями, комментариями и примерами тестов можно найти в репозитории JavaScript Algorithms и Data Structures.
Веселого кодинга!
Несколько похожих материалов
- 6 парадигм программирования, которые изменят ваше мнение о коде
- Хороший код: писать так, чтобы потом не было мучительно больно
- Принципы функционального программирования: почему это важно
Источник: ITNEXT




Комментарии