В Python большинство методов, связанных с линейной алгеброй, реализованы в scipy.linalg, которая содержит инструменты для эффективного решения задач.
Из этой статьи вы узнаете, как:
- Применять концепции линейной алгебры для решения практических задач с помощью scipy.linalg
- Работать с векторами и матрицами, используя Python и NumPy
- Моделировать практические задачи с помощью линейных систем
- Решать линейные системы с помощью scipy.linalg
Как только вы познакомитесь с линейными системами, вы будете готовы к изучению матриц и метода наименьших квадратов в следующем уроке из этой серии. А пока читайте дальше, чтобы начать работу с scipy.linalg.
Бесплатный исходный код: щелкните здесь, чтобы загрузить бесплатный код и набор данных, которые вы будете использовать для работы с линейными системами и алгеброй в Python с помощью scipy.linalg.
Начинаем работу с scipy.linalg
SciPy — это библиотека Python с открытым исходным кодом, используемая для научных вычислений, включающая несколько модулей для решения общих задач в науке и технике, таких как линейная алгебра, оптимизация, интегрирование, интерполяция и обработка сигналов. Это часть стека SciPy, который включает несколько других пакетов для научных вычислений, таких как NumPy, Matplotlib, SymPy, IPython и pandas.
Линейная алгебра — это раздел математики, который занимается линейными уравнениями и их представлениями с помощью векторов и матриц, и является фундаментальным предметом в нескольких областях инженерии. Знание линейной алгебры – необходимое условие для более глубокого понимания машинного обучения.
scipy.linalg включает в себя несколько инструментов для работы с задачами линейной алгебры, а именно функции для выполнения матричных вычислений, таких как определители, инверсии, собственные значения, собственные векторы и разложение по сингулярным значениям.
В данной статье будут использованы некоторые функции из scipy.linalg для решения практических задач, связанных с линейными системами. Чтобы использовать scipy.linalg, вам необходимо установить и настроить библиотеку SciPy, что вы можете сделать с помощью дистрибутива Python Anaconda и conda, системы управления пакетами и средой.
Примечание. Чтобы узнать больше об Anaconda и conda, ознакомьтесь с разделом «Настройка Python для машинного обучения в Windows» .
Для начала создайте среду conda и активируйте ее:
$ conda create --name linalg
$ conda activate linalg
После того, как вы активируете среду conda, в командной строке отобразится ее имя, linalg. Затем вы можете установить необходимые пакеты внутри среды:
(linalg) $ conda install scipy jupyter
После выполнения этой команды системе потребуется некоторое время, чтобы определить зависимости и продолжить установку.
Примечание. Помимо использования SciPy, вы также будете использовать Jupyter Notebook для запуска кода в интерактивной среде. Это необязательно, но облегчает работу с числовыми и научными приложениями.
Чтобы освежить в памяти работу с Jupyter Notebook, ознакомьтесь с Jupyter Notebook: An Introduction.
Если вы предпочитаете использовать другой дистрибутив Python с менеджером пакетов pip, разверните и посмотрите раздел ниже, чтобы узнать, как настроить среду:
Сначала необходимо создать виртуальную среду, в которой вы будете устанавливать пакеты. Предполагая, что у вас установлен Python, вы можете создать и активировать виртуальную среду под названием linalg:
Windows:
PS> python -m venv linalg
PS> .\linalg\Scripts\Activate
Linux:
$ python -m venv linalg
$ source ./linalg/bin/activate
После активации виртуальной среды в подсказке появится ее название – linalg. Затем вы можете установить необходимые пакеты внутри среды с помощью pip:
(linalg) $ python -m pip install scipy jupyter
Системе потребуется некоторое время, чтобы разобраться с зависимостями и продолжить установку. После завершения команды вы будете готовы использовать scipy.linalg и Jupyter.
Прежде чем открывать Jupyter Notebook, вам необходимо зарегистрировать linalg-среду, чтобы вы могли создавать Notebooks (т. е. использовать в качестве ядра). Для этого в активированной среде linalg выполните следующую команду:
(linalg) $ python -m ipykernel install --user --name linalg
Теперь вы можете открыть Jupyter Notebook, выполнив следующую команду:
$ jupyter notebook
После того, как Jupyter загрузится в вашем браузере, создайте новый Notebook, нажав на New → linalg, как показано ниже:
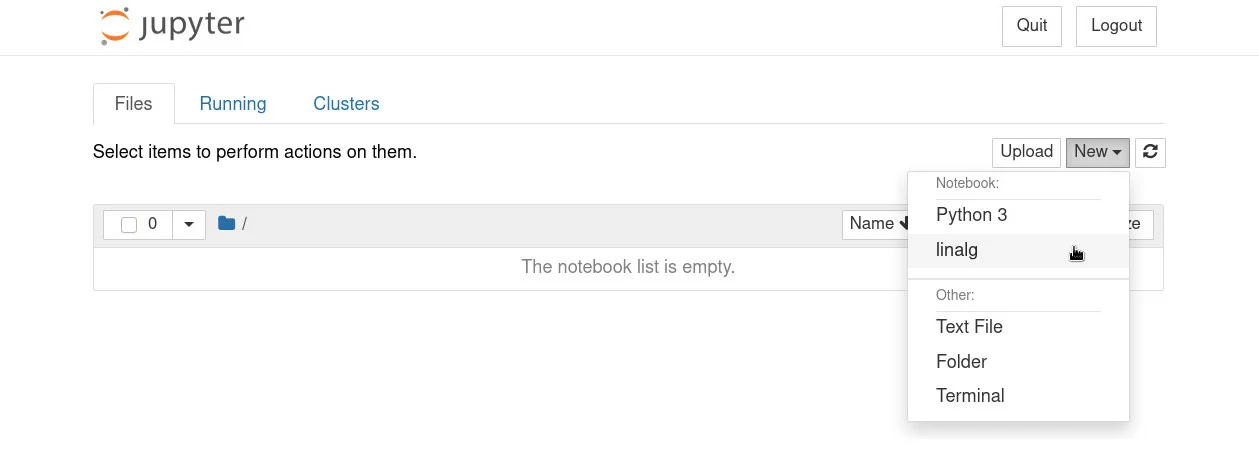
Внутри Notebook вы можете проверить успешность установки, импортировав пакет scipy:
In [1]: import scipy
Если вы не видите ошибки импорта, то все хорошо и можно продолжить.
Теперь, когда вы закончили настройку среды, разберем, как работать с векторами и матрицами в Python, что является основой для работы с приложениями линейной алгебры в scipy.linalg.
Работа с векторами и матрицами с помощью NumPy
Вектор — это математический объект, используемый для представления физических величин, которые имеют как величину, так и направление. Это фундаментальный инструмент для решения инженерных задач и задач машинного обучения. То же самое и с матрицами, которые используются для представления векторных преобразований, среди других приложений.
NumPy — это наиболее часто используемая библиотека для работы с матрицами и векторами в Python, которая используется вместе с scipy.linalg для работы с приложениями линейной алгебры. В этом разделе вы познакомитесь с основами его использования для создания матриц и векторов и выполнения над ними операций.
Чтобы начать работать с матрицами и векторами, первое, что вам нужно сделать в Jupyter Notebook, — это импортировать файлы numpy. Для этого вы можете использовать псевдоним np:
In [1]: import numpy as np
Для представления матриц и векторов NumPy использует специальный тип, называемый ndarray.
Для создания объекта ndarray вы можете использовать np.array(), который будет принимать на вход массивоподобный объект, такой как список или вложенный список.
В качестве примера, представьте, что вам нужно создать следующую матрицу:
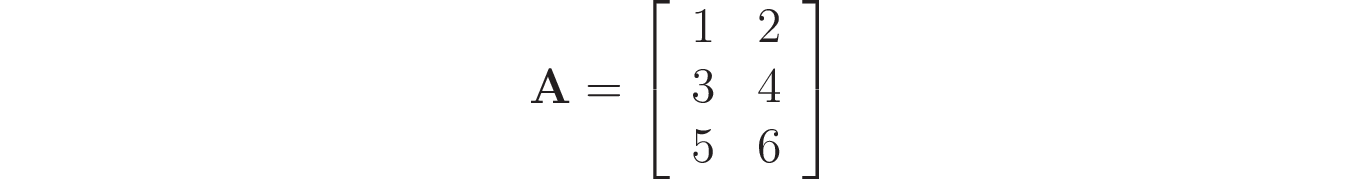
Чтобы создать ее с помощью NumPy, вы можете использовать np.array(), создавая вложенный список, содержащий элементы каждой строки матрицы:
In [2]: A = np.array([[1, 2], [3, 4], [5, 6]])
...: A
Out[2]:
array([[1, 2],
[3, 4],
[5, 6]])
Как вы могли заметить, NumPy обеспечивает визуальное представление матрицы, в котором вы можете идентифицировать ее столбцы и строки.
Стоит отметить, что элементы массива NumPy должны быть одного типа. Вы можете проверить тип массива NumPy, используя .dtype:
In [3]: A.dtype
Out[3]:
dtype('int64')
Поскольку все элементы A являются целыми числами, массив был создан с типом int64. Если один из элементов является числом с плавающей запятой, то массив будет создан с типом float64:
In [4]: A = np.array([[1.0, 2], [3, 4], [5, 6]])
...: A
Out[4]:
array([[1., 2.],
[3., 4.],
[5., 6.]])
In [5]: A.dtype
Out[5]:
dtype('float64')
Чтобы посмотреть размер ndarray-объекта, вы можете использовать .shape. Например, чтобы узнать размер A, вы можете использовать A.shape:
In [6]: A.shape
Out[6]:
(3, 2)
Как и ожидалось, размеры матрицы A равны 3×2, так как A содержит три строки и два столбца.
При работе с задачами, связанными с матрицами, вам часто придется использовать операцию транспонирования, которая меняет местами столбцы и строки матрицы.
Чтобы транспонировать вектор или матрицу, представленную ndarray-объектом, вы можете использовать .transpose()или .T. Например, вы можете выполнить транспонирование A с помощью A.T:
In [7]: A.T
Out[7]:
array([[1., 3., 5.],
[2., 4., 6.]])
При транспонировании столбцы A становятся строками A.T, а строки становятся столбцами.
Чтобы создать вектор, вы используете np.array(), создавая список с элементами вектора:
In [8]: v = np.array([1, 2, 3])
...: v
Out[8]:
array([1, 2, 3])
Чтобы проверить размеры вектора, вы можете использовать .shape, как и раньше:
In [9]: v.shape
Out[9]:
(3,)
Обратите внимание, что форма этого вектора (3,), а не (3, 1) или (1, 3). Это функция NumPy, которая актуальна, если вы привыкли работать с MATLAB. В NumPy можно создавать одномерные массивы, такие как v, что может вызвать проблемы при выполнении операций между матрицами и векторами. Например, операция транспонирования не влияет на одномерные массивы.
Всякий раз, когда вы передаете аргумент, подобный одномерному массиву np.array(), результирующий массив будет одномерным массивом. Чтобы создать двумерный массив, вы должны передать аргумент, подобный двумерному массиву, например, вложенный список:
In [10]: v = np.array([[1, 2, 3]])
...: v.shape
Out[10]:
(1, 3)
В приведенном выше примере размеры v равны 1× 3, что соответствует размерам двумерного вектора-строки. Чтобы создать вектор-столбец, вы можете использовать вложенный список:
In [11]: v = np.array([[1], [2], [3]])
...: v.shape
Out[11]:
(3, 1)
В этом случае размеры v равны 3× 1, что соответствует размерам двумерного вектора-столбца.
Использование вложенных списков для создания векторов может быть трудоемким, особенно для векторов-столбцов, которые вы, вероятно, будете использовать чаще всего. В качестве альтернативы вы можете создать одномерный вектор, передав плоский список в np.array, и использовать .reshape() для изменения размера объекта ndarray:
In [12]: v = np.array([1, 2, 3]).reshape(3, 1)
...: v.shape
Out[12]:
(3, 1)
В приведенном выше примере вы используете .reshape() для получения вектор-столбца вида (3, 1) из одномерного вектора вида (3,). Стоит отметить, что в случае использования .reshape() необходимо, чтобы количество элементов нового массива было совместимо с количеством элементов исходного массива. Другими словами, количество элементов в новом массиве должно быть равно количеству элементов в исходном массиве.
В этом примере вы также можете использовать .reshape() без явного определения количества строк массива:
In [13]: v = np.array([1, 2, 3]).reshape(-1, 1)
...: v.shape
Out[13]:
(3, 1)
Здесь , -1, который вы передаете в качестве аргумента в .reshape(),представляет количество строк, необходимых для того, чтобы новый массив имел только один столбец, как указано вторым аргументом. В этом случае, поскольку исходный массив состоит из трех элементов, количество строк в новом массиве будет равно 3.
На практике вам часто нужно создавать матрицы из нулей, единиц или случайных элементов. Для этого NumPy предоставляет некоторые удобные функции, которые вы увидите далее.
Использование вспомогательных функций для создания массивов
NumPy также предоставляет некоторые удобные функции для создания массивов. Например, чтобы создать массив, заполненный нулями, вы можете использовать np.zeros():
In [1]: import numpy as np
In [2]: np.zeros((3, 2))
Out[2]:
array([[0., 0.],
[0., 0.],
[0., 0.]])
В качестве первого аргумента np.zeros()должен быть кортеж, указывающий форму массива, который вы хотите создать, и возвращает массив типа float64.
Примечание. Чтобы указать тип создаваемого массива np.zeros(), вы можете задать аргумент для dtype. Например, np.zeros((3, 2), dtype=int) создает массив целых чисел.
Точно так же для создания массивов, заполненных единицами, вы можете использовать np.ones():
In [3]: np.ones((2, 3))
Out[3]:
array([[1., 1., 1.],
[1., 1., 1.]])
Стоит отметить, что np.ones() также возвращает массив типа float64.
Чтобы создать массивы со случайными элементами, вы можете использовать np.random.rand():
In [4]: np.random.rand(3, 2)
Out[4]:
array([[0.8206045 , 0.54470809],
[0.9490381 , 0.05677859],
[0.71148476, 0.4709059 ]])
np.random.rand() возвращает массив случайных чисел между 0 и 1, взятых из равномерного распределения. Обратите внимание, что, в отличие от np.zeros() и np.ones(), np.random.rand() не ожидает кортеж в качестве аргумента.
Точно так же, чтобы получить массив со случайными элементами, взятыми из нормального распределения с нулевым средним значением и единичной дисперсией, вы можете использовать np.random.randn():
In [5]: np.random.randn(3, 2)
Out[5]:
array([[-1.20019512, -1.78337814],
[-0.22135221, -0.38805899],
[ 0.17620202, -2.05176764]])
Теперь, когда вы прошли через создание массивов, вы увидите, как выполнять с ними операции.
Выполнение операций с массивами NumPy
Обычные операции Python с использованием операций сложения (+), вычитания (-), умножения (*), деления ( /) и возведения в степень (**) над массивами всегда выполняются поэлементно. Если один из операндов является скаляром, вы будете выполнять операцию между скаляром и каждым элементом массива.
Например, чтобы создать матрицу, заполненную элементами, равными 10, вы можете использовать np.ones() и умножить полученное значение на 10 с помощью оператора * :
In [1]: import numpy as np
In [2]: 10 * np.ones((2, 2))
Out[2]:
array([[10., 10.],
[10., 10.]])
Если оба операнда являются массивами одинакового вида, то операция будет выполняться между соответствующими элементами массивов:
In [3]: A = 10 * np.ones((2, 2))
...: B = np.array([[2, 2], [5, 5]])
...: A * B
Out[3]:
array([[20., 20.],
[50., 50.]])
Здесь вы умножаете каждый элемент матрицы A на соответствующий элемент матрицы B.
Чтобы выполнить умножение матриц в соответствии с правилами линейной алгебры, вы можете использовать оператор умножения матриц (@):
In [4]: A = np.array([[1, 2], [3, 4]])
...: v = np.array([[5], [6]])
...: A @ v
Out[4]:
array([[17],
[39]])
Здесь вы умножаете A-матрицу 2 × 2 на вектор 2 × 1 с именем v.
Вы можете получить тот же результат, используя np.dot(), хотя вместо него рекомендуется использовать @:
In [5]: A = np.array([[1, 2], [3, 4]])
...: v = np.array([[5], [6]])
...: np.dot(A, v)
Out[5]:
array([[17],
[39]])
Помимо основных операций для работы с матрицами и векторами, NumPy также предоставляет некоторые специальные функции для работы с линейной алгеброй в numpy.linalg. Однако scipy.linalg обладает еще некоторыми преимуществами, которые мы рассмотрим далее.
Сравнение scipy.linalg с numpy.linalg
NumPy включает в модуль numpy.linalg некоторые инструменты для работы с приложениями линейной алгебры . Однако, если вы не хотите добавлять SciPy в качестве зависимости в свой проект, обычно лучше использовать scipy.linalg по следующим причинам:
- Как поясняется в официальной документации, scipy.linalg содержит все функции в numpy.linalg плюс некоторые дополнительные расширенные функции, которые не включены в
numpy.linalg. scipy.linalgвсегда компилируется с поддержкой BLAS и LAPACK, которые представляют собой библиотеки, включающие методы для выполнения числовых операций оптимизированным способом. В случаеnumpy.linalgиспользование BLAS и LAPACK необязательно. Таким образом, в зависимости от того как вы устанавливаете NumPy, функцииscipy.linalgмогут работать быстрее, чем функции изnumpy.linalg.
Учитывая, что научные и технические приложения, как правило, не имеют ограничений в отношении зависимостей, рекомендуется установить SciPy и использовать scipy.linalg вместо numpy.linalg.
В следующем разделе мы будем использовать инструменты scipy.linalg для работы с линейными системами. Вы начнете с изучения основ на простом примере, а затем примените концепции к практической задаче.
Использование scipy.linalg.solve()для решения линейных систем
Линейные системы могут быть полезным инструментом для поиска решения нескольких прикладных и важных проблем, включая проблемы, связанные с движением транспортных средств, химическими уравнениями, электрическими цепями и полиномиальной интерполяцией.
В этом разделе вы узнаете, как использовать scipy.linalg.solve()для решения линейных систем. Но, прежде чем приступить к работе с кодом, важно понять основы.
Знакомство с линейными системами
Линейная система или, точнее, система линейных уравнений — это набор уравнений, линейно относящихся к набору переменных. Вот пример линейной системы, относящейся к переменным x ₁, x ₂ и x ₃:
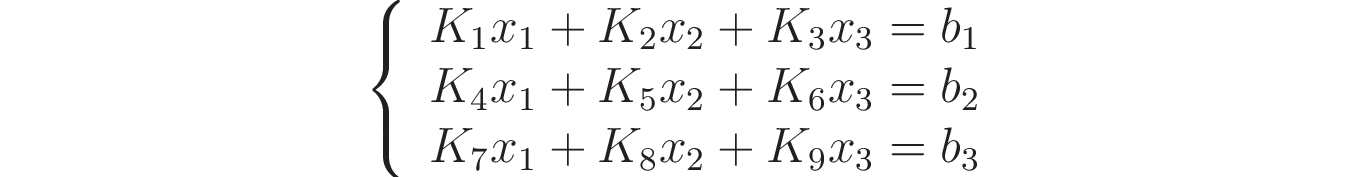
Здесь у вас есть три уравнения с тремя переменными. Чтобы система была линейной, значения K ₁, …, K ₉ и b ₁, b ₂, b ₃ должны быть константами.
Когда есть только два или три уравнения и две или три переменных, можно выполнить расчеты вручную, объединить уравнения и найти значения для переменных. Однако при наличии четырех и более переменных ручное решение линейной системы занимает значительное время, и возрастает риск совершения ошибок.
Прикладные приложения обычно включают большое количество переменных, что делает невозможным решение линейных систем вручную. К счастью, есть несколько инструментов, которые могут выполнять эту тяжелую работу, например scipy.linalg.solve().
Использование scipy.linalg.solve()
SciPy позволяет scipy.linalg.solve() быстро и надежно решать линейные системы. Чтобы понять, как это работает, рассмотрим следующую систему:
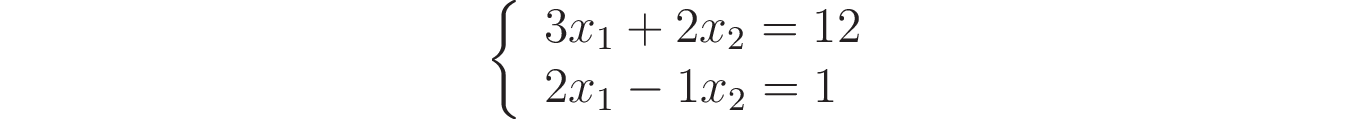
Чтобы использовать scipy.linalg.solve(), вам нужно сначала записать линейную систему в виде матричного произведения, как в следующем уравнении:
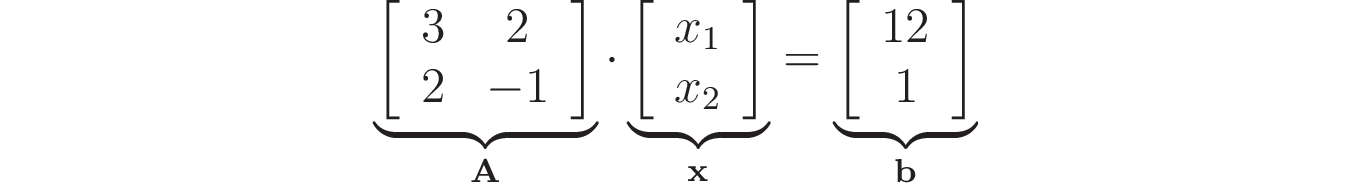
Обратите внимание, что вы получите исходные уравнения системы после вычисления матричного произведения. Ожидаемые входные данные scipy.linalg.solve() — это матрица A и вектор b, которые вы можете определить с помощью массивов NumPy. Таким образом, вы можете решить систему, используя следующий код:
In [1]: import numpy as np
...: from scipy import linalg
In [2]: A = np.array(
...: [
...: [3, 2],
...: [2, -1],
...: ]
...: )
In [3]: b = np.array([12, 1]).reshape((2, 1))
In [4]: x = linalg.solve(A, b)
...: x
Out[4]:
array([[2.],
[3.]])
Вот разбивка того, что происходит:
- Строки 1 и 2 импортируют NumPy как np, а также
linalgизscipy. - Строки с 4 по 9 создают матрицу коэффициентов в виде массива NumPy и называют ее
A. - В строке 11 создается вектор независимых терминов с использованием массива NumPy с именем
b. Чтобы сделать его вектор-столбцом с двумя линиями, вы используете.reshape((2, 1)). - Строки 13 и 14 призывают
linalg.solve()для решения линейной системы, характеризуемойAиb, с сохранением результата в результатx. Обратите внимание, что решениеsolve()возвращает компоненты с плавающей запятой, хотя все элементы исходных массивов являются целыми числами.
Если заменить x₁ = 2 и x₂ = 3 в исходных уравнениях, то можно убедиться, что это решение системы.
Теперь, когда вы ознакомились с основами использования scipy.linalg.solve(), пришло время попробовать практическое применение линейных систем.
Решение практической задачи: составление плана питания
Одна из проблем, которую вы обычно решаете с помощью линейных систем, — это когда вам нужно найти пропорции компонентов, необходимых для получения определенной смеси. Ниже вы собираетесь использовать эту идею для построения плана питания, смешивая разные продукты, чтобы получить сбалансированную диету.
Для этого предположим, что сбалансированная диета должна включать следующее:
- 170 единиц витамина А
- 180 единиц витамина В
- 140 единиц витамина С
- 180 единиц витамина D
- 350 единиц витамина Е
Ваша задача состоит в том, чтобы найти количество каждого отдельного продукта, чтобы получить указанное количество необходимых витаминов. В следующей таблице представлены результаты анализа одного грамма каждого продукта в пересчете на единицы каждого витамина:
| Продукт | Витамин A | Витамин B | Витамин C | Витамин D | Витамин E |
| #1 | 1 | 10 | 1 | 2 | 2 |
| #2 | 9 | 1 | 0 | 1 | 1 |
| #3 | 2 | 2 | 5 | 1 | 2 |
| #4 | 1 | 1 | 1 | 2 | 13 |
| #5 | 1 | 1 | 1 | 9 | 2 |
Обозначая продукт 1 как x ₁ и т. д. и учитывая, что вы собираетесь смешать x ₁ единиц продукта 1, x ₂ единиц продукта 2 и т. д., вы можете написать выражение для количества витамина А, которое вы получите в рационе. Учитывая, что сбалансированная диета должна включать 170 единиц витамина А, вы можете использовать данные из столбца Витамин А, чтобы написать следующее уравнение:

Повторяя ту же процедуру для витаминов B, C, D и E, вы получите следующую линейную систему:
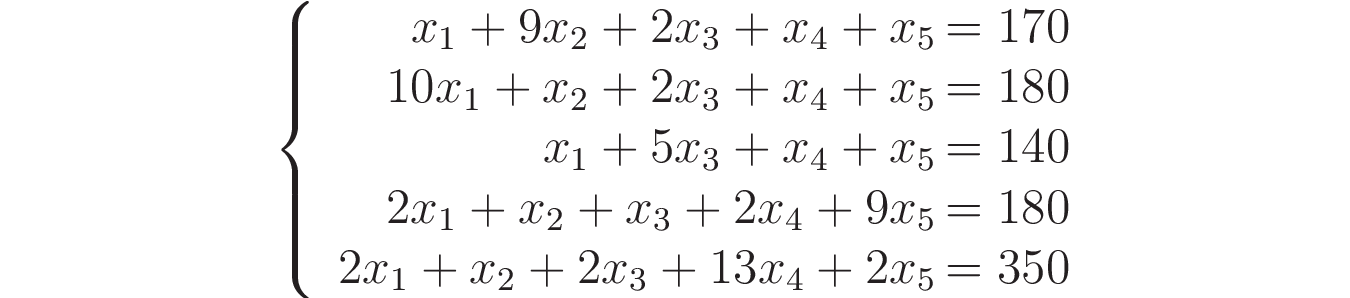
Чтобы использовать scipy.linalg.solve(), вы должны получить матрицу коэффициентов A и вектор независимых членов b, которые задаются следующим образом:

Теперь вы можете использовать scipy.linalg.solve(), чтобы узнать величины x ₁, …, x ₅:
In [1]: import numpy as np
...: from scipy import linalg
In [2]: A = np.array(
...: [
...: [1, 9, 2, 1, 1],
...: [10, 1, 2, 1, 1],
...: [1, 0, 5, 1, 1],
...: [2, 1, 1, 2, 9],
...: [2, 1, 2, 13, 2],
...: ]
...: )
In [3]: b = np.array([170, 180, 140, 180, 350]).reshape((5, 1))
In [4]: x = linalg.solve(A, b)
...: x
Out[4]:
array([[10.],
[10.],
[20.],
[20.],
[10.]])
Это указывает на то, что сбалансированный рацион должен включать 10 единиц пищи 1, 10 единиц пищи 2, 20 единиц пищи 3, 20 единиц пищи 4 и 10 единицы пищи 5.
Заключение
Поздравляем! Вы узнали, как применить некоторые концепции линейной алгебры и как применить scipy.linalg для решения задач, связанных с линейными системами. Вы убедились, что векторы и матрицы полезны для представления данных и что, используя концепции линейной алгебры, вы можете моделировать решения практических проблем и эффективно их решать.
Из этой статьи вы узнали, как:
- Применять концепции линейной алгебры для решения практических задач с помощью scipy.linalg
- Работать с векторами и матрицами, используя Python и NumPy
- Моделировать практические задачи с помощью линейных систем
- Решать линейные системы с помощью scipy.linalg



Комментарии