Эпоха автоматизации, машинного обучения и анализа данных естественным образом касается и синтеза материалов. Химия по своей природе включает в себя широкий спектр случайных процессов, однако химики почти не исследуют стохастичность на макроуровне из-за сложности сбора данных.
В недавно опубликованной работе в журнале Matter исследователи из Университета Глазго задались вопросом: можно ли систематически изучить процесс кристаллизации с использованием автономной роботизированной платформы?
Учёные проконтролировали кристаллизацию сотен параллельных реакций с помощью веб-камеры и обнаружили, что особенности роста кристаллов на полученных изображениях можно использовать для генерации истинно случайных чисел.
Было устанолено, что информационная энтропия различна для разных типов химических реакций, а способность шифрования с помощью генерируемых случайных чисел не хуже, чем у наиболее часто используемого генератора псевдослучайных чисел.
Общая идея эксперимента
Случайные числа широко используются во многих приложениях, таких как криптография и научное моделирование, где важное значение имеет их непредсказуемость. Источник случайности определяет, будет ли наблюдаться корреляция между генерируемыми числами.
В отличие от компьютерных методов нахождения случайных чисел (генераторов псевдослучайных чисел), химические процессы имеет гораздо более сложные источники энтропии. При проведении реакции существует практически бесконечное число энергетически эквивалентных способов объединения молекул реагентов, что приводит к высокой неопределённости. Точный путь, по которому идёт реакция, никогда не повторяется. Общий результат – одно состояние из бесчисленного ряда возможных.
Таким образом, энтропия химической системы может служить хорошим пулом для генерации случайных чисел. Одной из систем с большим энтропийным пулом является система образования соединений с последующей кристаллизацией.
Чтобы проверить эту идею, исследователи разработали полностью автоматизированную систему, которая запускала химическую реакцию, выращивала кристаллы и анализировала результат, используя в качестве детектора веб-камеру.
Платформа была спроектирована таким образом, чтобы преобразовывать данные о выросших кристаллах в двоичные последовательности, как это показано на схеме ниже.
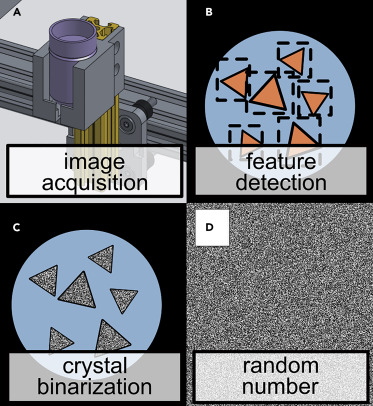
- A – захват изображение
- B – детектирование особенностей
- C – бинаризация кристаллов
- D – получение случайных чисел
Как проводился эксперимент
Процесс кристаллизации запускался параллельно во множестве ячеек с помощью роботизированной платформы на основе станка с ЧПУ. Исходные растворы реагентов располагались рядом с платформой и переносились с помощью системы насосов и трубок в матрицу 10 × 10 миниатюрных реакторов, где и происходила кристаллизация.

Кристаллизацию в каждом реакторе регистрировали с интервалом 10 минут мобильной камерой с разрешением 1280 × 800. Для анализа изображения и определения местоположения кристаллов в реакторах использовался алгоритм детектирования и сегментации Mask R-CNN. Этот же алгоритм используется для аналогичных задач в Data Science.
Исходные реагенты были выбраны так, чтобы обеспечить рост различимых кристаллов в масштабе времени от нескольких минут до нескольких часов. Расположение, размер, форма, ориентация и цвет растущих кристалликов использовались в качестве источника информационной энтропии для рассматриваемой системы.
Учёные провели реакции, которые включали химические процессы различной сложности:
- Только кристаллизацию.
- Образование химических кластеров с последующей кристаллизацией.
- Взаимодействие химических комплексов с малыми молекулами с последующим образованием кластеров и кристаллизацией.
Исследователи предположили, что увеличение числа химических процессов повышает количество возможных микросостояний, а, значит, вырастет информационная энтропия системы.
Трём вышеперечисленным пунктам соответствуют три реакции:
- Перекристаллизация неорганической соли медного купороса.
- Синтез и кристаллизация полиоксометаллатной соли вольфрама.
- Синтез и кристаллизация координационного кластера кобальта.
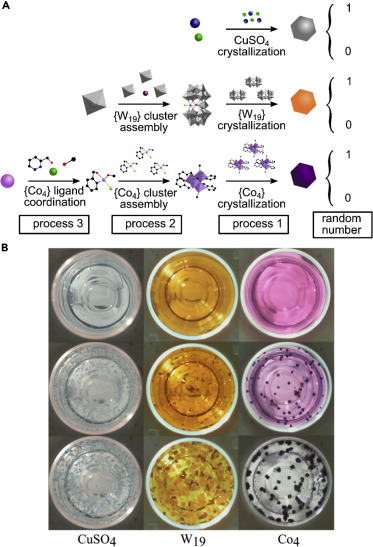
Химическая структура и снимки процессов в различные моменты времени показаны на рисунке выше. Эксперименты проводились полностью автоматизированным способом. Кристаллическая природа соединений была подтверждена методом дифракции рентгеновских лучей.
Затем была сгенерирована двоичная последовательность. Каждый кристалл определял последовательность из 5 байт, задававшихся размером, ориентацией и цветом кристалла. Эти последовательности объединялись у смежных кристаллов для генерации длинной двоичной последовательности. Та разделялась на секции по 64 байта, к каждой из которых применялся алгоритм sha512. Полученные последовательности вновь объединялись для формирования конечной строки.
Оценка случайности производилась методами, описанными в специальной публикации Национального института стандартов и технологий (NIST) 800-22a.15. На рисунке ниже приведены результаты прохождения тестов и гистограммы распределения p-уровня значимости в случае первой реакции. Все тесты подтвердили, что генерируемые последовательности имеют случайную природу (обратите внимание на величину pass rate).

Также было подтверждено, что информационная энтропия имеет различное распределение для трёх указанных реакций.
Наконец, поскольку среди применений случайных чисел важное значение имеет вопрос шифрования данных, было проведено сравнение «химической» генерации случайных чисел с часто используемым генератором псевдослучайных чисел – вихрем Мерсенна (англ. Mersenne Twister, MT)
Поскольку выход вихря Мерсенна определяется на основе внутреннего состояния, знание состояния позволяет спрогнозировать будущий результат. В то же время в случае генератора истинно случайных чисел внутреннее состояние невозможно определить из-за энтропии физического процесса.
Чтобы показать возможность применения подхода, исследователи зашифровали ASCII-строку "crystal!", используя последовательности чисел, созданные химическим генератором случайных чисел и вихрем Мерсенна.
Затем они сравнили среднее время, необходимое для нахождения правильного ключа и расшифровки сообщения. В обоих случаях использовалась дешифровка методом «грубой силы». В случае вихря Мерсенна знание предыдущих успешных ключей позволило определить состояние генератора и, спрогнозировать весь будущий вывод, что, очевидно, свело время дешифровки к нулю.
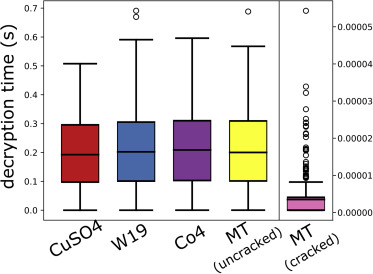
Бокс-плоты для расшифровки 5 тысяч 8-битных ключей, представлены на рисунке выше и показывают, что среднее время дешифровки ключей одинаково для последовательностей, сгенерированных с помощью роста кристаллов и полученных вихрем Мерсенна. Однако сама физическая природа генерации чисел не позволяет «взломать» систему.
Хотя скорость генерации битов описанным способом значительно ниже, чем в других методах (до ~ 25 кБ/с), исследователи считают, что разработанный подход позволяет повысить криптографическую безопасность выходных данных.
Понятно, что в практическом смысле такой подход – это пока скорее забавный казус, а не улучшение качества шифрования. Но и от него есть польза: измерение информационной энтропии реакций – полезное средство для оценки сложности сходных химических систем.



Комментарии