Условие задачи
Рассмотрим карточную игру для одного человека. У игрока 13 карт одной масти. Каждой карте присвоено числовое значение. Туз, валет, дама, король соответствуют 1, 11, 12 и 13. Перед началом игры карты перемешиваются. Далее циклически повторяется следующая операция.
Поднимается верхняя карта колоды. Если это туз, игра останавливается. В противном случае (если N != 1), N карт, включая поднятую, снимаются с колоды и вновь кладутся сверху, но в обратном порядке.
Пример шага игры:
5 7 10 K 8 Т 3 Д В 4 9 2 6 ⇒ 8 K 10 7 5 Т 3 Д В 4 9 2 6
Вопрос: Всегда ли игра останавливается после конечного числа итераций для любого начального состояния колоды? Объясните свой ответ.
Решение – в следущей задаче.
Эта задача – двенадцатый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую загадку Чеширского Кота.
Решение загадки Чеширского Кота
Ответ: 63504.
Решение. Нужно учесть симметрию ромба и начать с подсчёта количества способов написания подстроки CAT I SAW. Любая такая строка начинается в центре буквы С и содержится в одном из четырёх треугольников, разделенных диагоналями ромба. Один из этих треугольников показан ниже на рисунке.
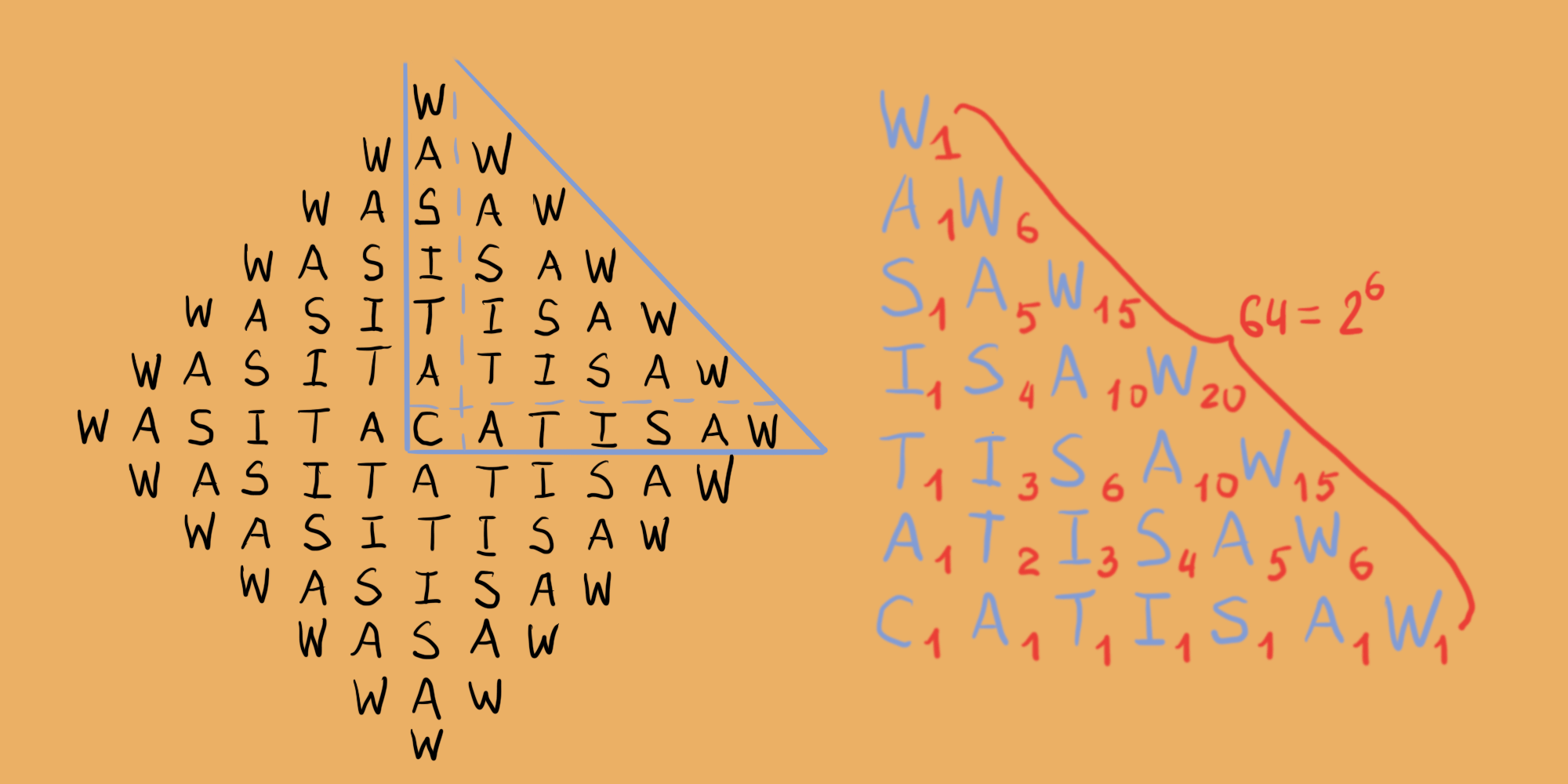
Количество строк CAT I SAW в треугольнике можно найти с помощью стандартного метода динамического программирования. Мы использовали его в одной из предыдущих задач.
Чтобы найти все пути, нужно двигаться от катетов треугольника к гипотенузе. Можно видеть, что эти числа образуют треугольник Паскаля. Сумма чисел на гипотенузе треугольника (границе ромба) равна 26. Тогда общее количество строк CAT I SAW для всего ромба находится по формуле 4·26 – 4. Четвёрку нужно вычесть, чтобы компенсировать избыточный подсчёт строк вдоль диагоналей ромба.
Это означает, что общее количество способов прочтения палиндрома WAS IT A CAT I SAW составляет (4·26 – 4)2 = 63504.
Как ответили читатели Библиотеки программиста? Слегка другим путём (без учёта симметрии), но к тому же результат пришёл пользователь randomadman:
Не лучшим образом, в лоб, но решение. Для произнесения нам необходимо добраться от периферии к центру за буквой С и вернуться обратно. Ответом будет произведение количества путей до центра(А) и количества путей от центра(В). .Палиндром предполагает симметрию, а следовательно обратных путей будет столько же. А=В Нам нужно посчитать количество путей от периферии к центру. Обозначим финиш за единицу и графически подсчитаем количество путей из каждой точки на периферии. Результатом первого этапа будет сумма этих значений. получим 252. Ответ 252х252= 63504.
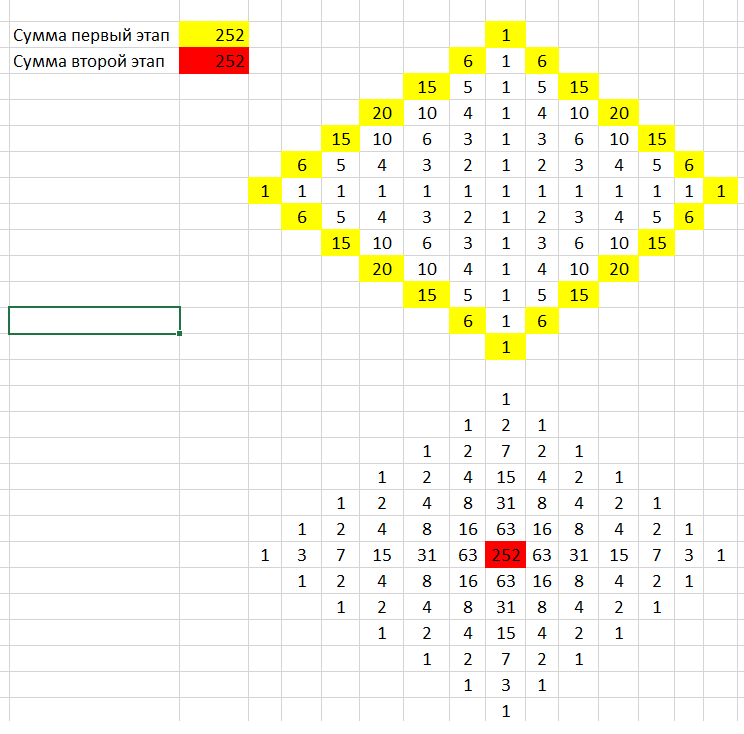
На поясняющем рисунке можно видеть тот же треугольник, что получился в нашем решении.




Комментарии