Семь гномиков

В Slack-канале чудесного сообщества Open Data Science есть раздел #gnomiki (назван по этой головоломке). Канал посвящен задачам, заданным на собеседованиях в IT-компании или тем, которые могли бы задать сами участники.

Ниже мы привели в порядке возрастания сложности семь задач-гномиков, не требующих длительного описания решения. В спойлерах – ответы, данные пользователями сообщества. Но не подглядывайте, постарайтесь сначала найти решение самостоятельно.

1. Простая задача про два числа

Начнем с очень простой задачи. Есть два числа, десятичные представления которых ни в одном разряде не содержат нуля. Но при перемножении два числа дают миллион. Что это за числа?

2. Автомат по розливу чая и кофе

Автомат по розливу чая и кофе имеет три кнопки: «чай», «кофе», «чай или кофе». Первые две наливают то, что написано, третья каждый раз случайным образом делает выбор и наливает либо чай, либо кофе. Бирки с кнопок отвалились и их приклеили наугад так, что ни одна из бирок не попала на своё место. Сколько нажатий потребуется, чтобы однозначно определить где какая кнопка?

3. Периметр фигуры

Определите периметр фигуры, если все её углы прямые.

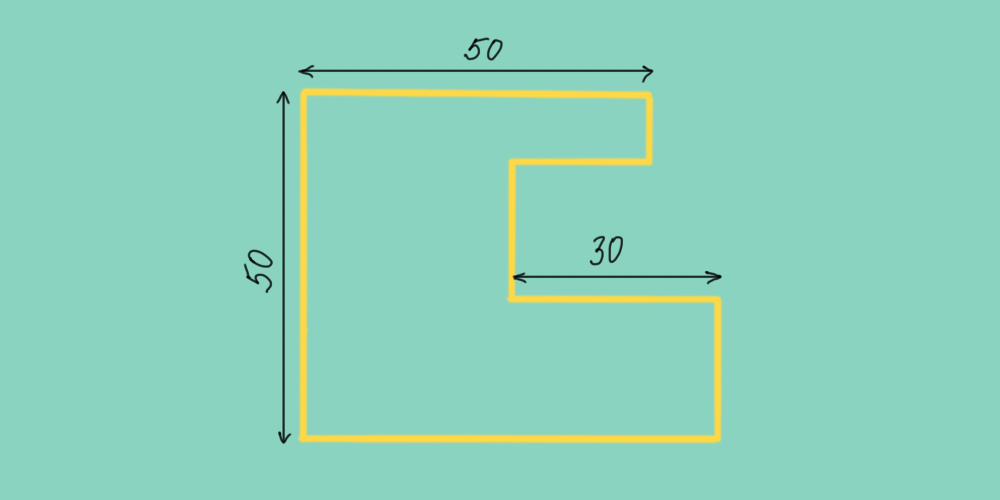
4. Вероятность найти деньги

Есть четыре коробки, человек говорит: «В одной из коробок с вероятностью 50% есть деньги». Открыли 3 коробки – пусто. Какова вероятность, что деньги в четвертой?»

5. Волшебный некрошащийся пирог

Вам принесли волшебный некрошащийся пирог, покрытый сверху шоколадом. Вы вырезали из пирога кусок в x радиан, перевернули и вставили обратно. Кусок удивительным образом сросся с пирогом. Потом вырезали следующий кусок в x радиан, так что начало нового куска совпадает с концом предыдущего, и так далее. При каких x рано или поздно весь шоколад опять окажется сверху?

6. Матожидание и макаронные кольца

В кастрюле варятся N длинных макаронин. Повар не глядя берет два свободных конца, связывает их и повторяет этот процесс до тех пор, пока не кончатся макаронины со свободными концами. Найти мат ожидание количества макаронных колец (кольцо может состоять не из одной макаронины).

7. Кажется, дождь собирается

Вы собираетесь на работу, вероятность, что идет дождь P. Если дождь идет, то вы берете зонтик. Вечером вы возвращаетесь с работы, вероятность дождя опять P. Если идет дождь и зонтик оказался на работе, то вы его берёте с собой. Сколько поездок в среднем можно совершить прежде, чем промокнешь?

Сериал головоломок. Итоги первого сезона

Этим постом мы также завершаем первый сезон сериала головоломок. Поддерживать его было трудно, но интересно. Нам особенно было радостно, когда наши читатели находили решения, и описывали их на сайте или в соцсетях. Вот все 15 серий, в каждой есть условие, к каждой дано решение в следующем номере. К последней задаче ответ дан в конце этого поста.

1. Двойные фамилии
2. Спрятанное решение
3. Остров хамелеонов
4. Номер Тьюринга
5. Время великих учёных
6. Прогуливающиеся джентльмены
7. Часы с одинаковыми стрелками
8. Вирус в колонии бактерий
9. Шесть шахматных коней
10. Задача о беглеце
11. Чеширский кот и число палиндромов
12. Карточная головоломка Конвея
13. Задача о необычном замке
14. Алгоритмическая головоломка о лягушках
15. Задача Сфинкса о разрезании лестниц

Пишите в комментариях, понравились ли вам эти сложные задачи на логику и алгоритмы. Лайкните этот пост, если вам понравился формат и вы ждёте продолжения сериала.

Решение задачи о разрезании лестниц

Если вы не решали эту задачу, прежде чем читать приведенный ниже текст, прочитайте условие и попробуйте решить самостоятельно!

Ответ. Первым очевидным решением является уже «разрезанный вариант», состоящий из самой фигуры тримино, то есть n = 2. Все остальные ответы можно выразить так: разрезание возможно для любого n, которое можно представить в виде n = 3k или n = 3k+2, где k > 1.

Решение и алгоритм разрезания «лестниц». Очевидно, что разрезание на тримино в первую очередь возможно только, если сама лестничная фигура делится без остатка на 3. Общее число квадратов в фигуре определяется как сумма арифметической прогрессии, то есть:

Если n = 3k, а k – четное (k = 2m), то

Тогда число квадратов делится на 3.

В случае если n = 3k и k – нечетное ( k = 2m + 1)

То есть вновь суммарное число квадратов делится на 3.

Аналогично можно показать, что для n = 3k + 1 деление всех квадратов на 3 без остатка невозможно, а для n = 3k + 2 вновь работает и для четных, и для нечетных k.

Как мы указали в подсказке к задаче хорошей идеей будет попытаться решить задачу для n, равных 3, 5, 6, 9, а далее – обобщить результаты.

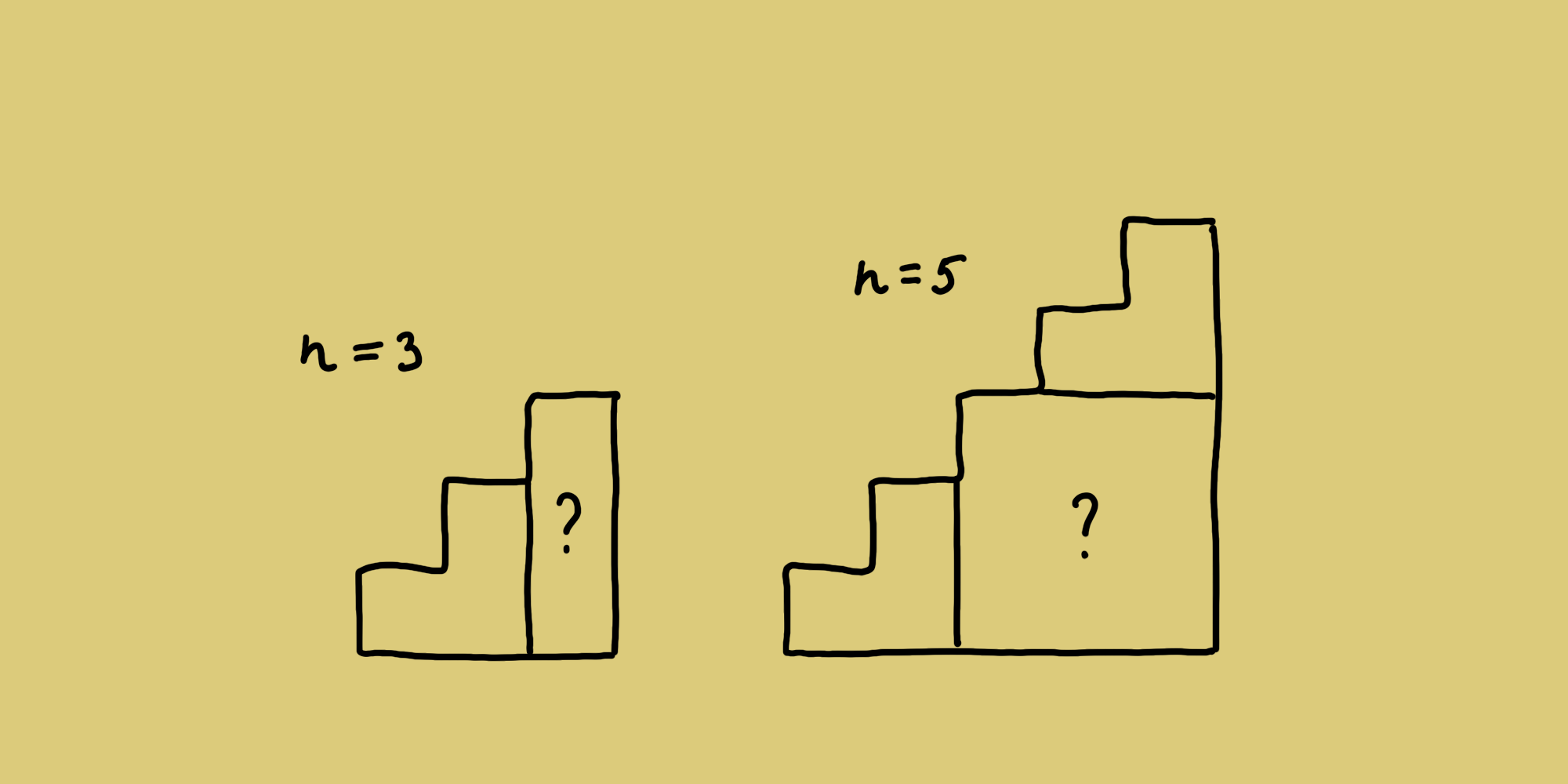
Следующие рисунки демонстрируют невозможность разрезать «лестницы» для n = 3 и n = 5.

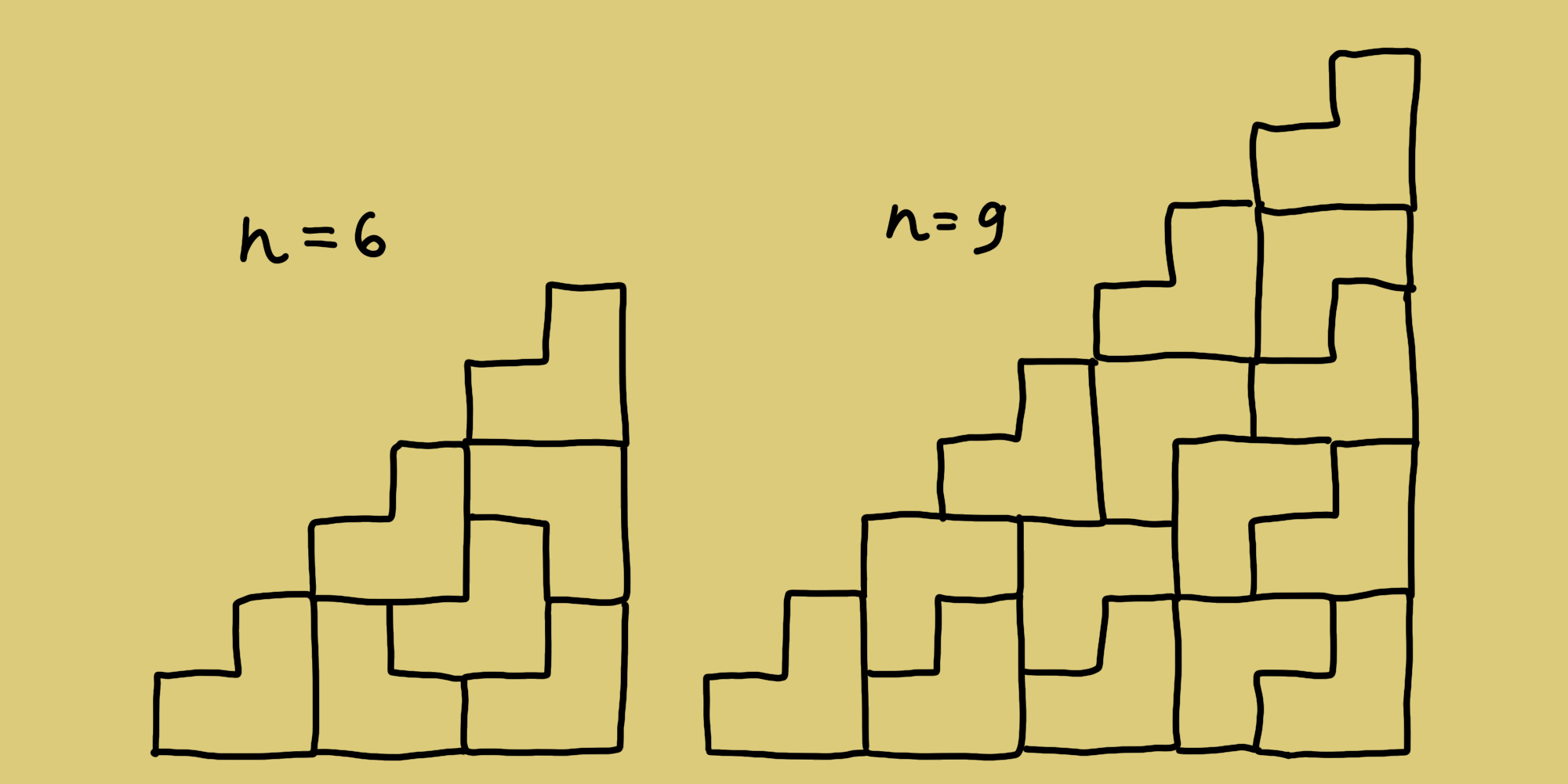
Теперь покажем, что любая лестница, для которой n = 3k и k > 1, может быть выложена плиткой из тримино по рекурсивному алгоритму. Возьмем первые примеры c k = 2 (n = 6) и k = 3 (n = 9).

Если n = 3k и k – четное целое число большее или равное 2 (т. е. n = 6m = 6 + 6(m – 1), где m > 1), лестница может быть разрезана на три составляющие:

• лестницу для n = 6, способ разрезания для которой показан выше,
• лестницу для n = 6 (m-1), которую можно замостить рекурсивно с помощью этого описания,
• прямоугольник размером 6 × 6 (m – 1), который разбивается на прямоугольники 3 × 2, каждый из которых представляет собой две сцепленных фигурки тримино.

Если n = 3k и k – нечетное целое число:

• лестницу для n = 9,
• лестницу для n = 6(m-1),
• прямоугольник размером 9 × 6(m – 1).

Оба случая представлены ниже на рисунке.

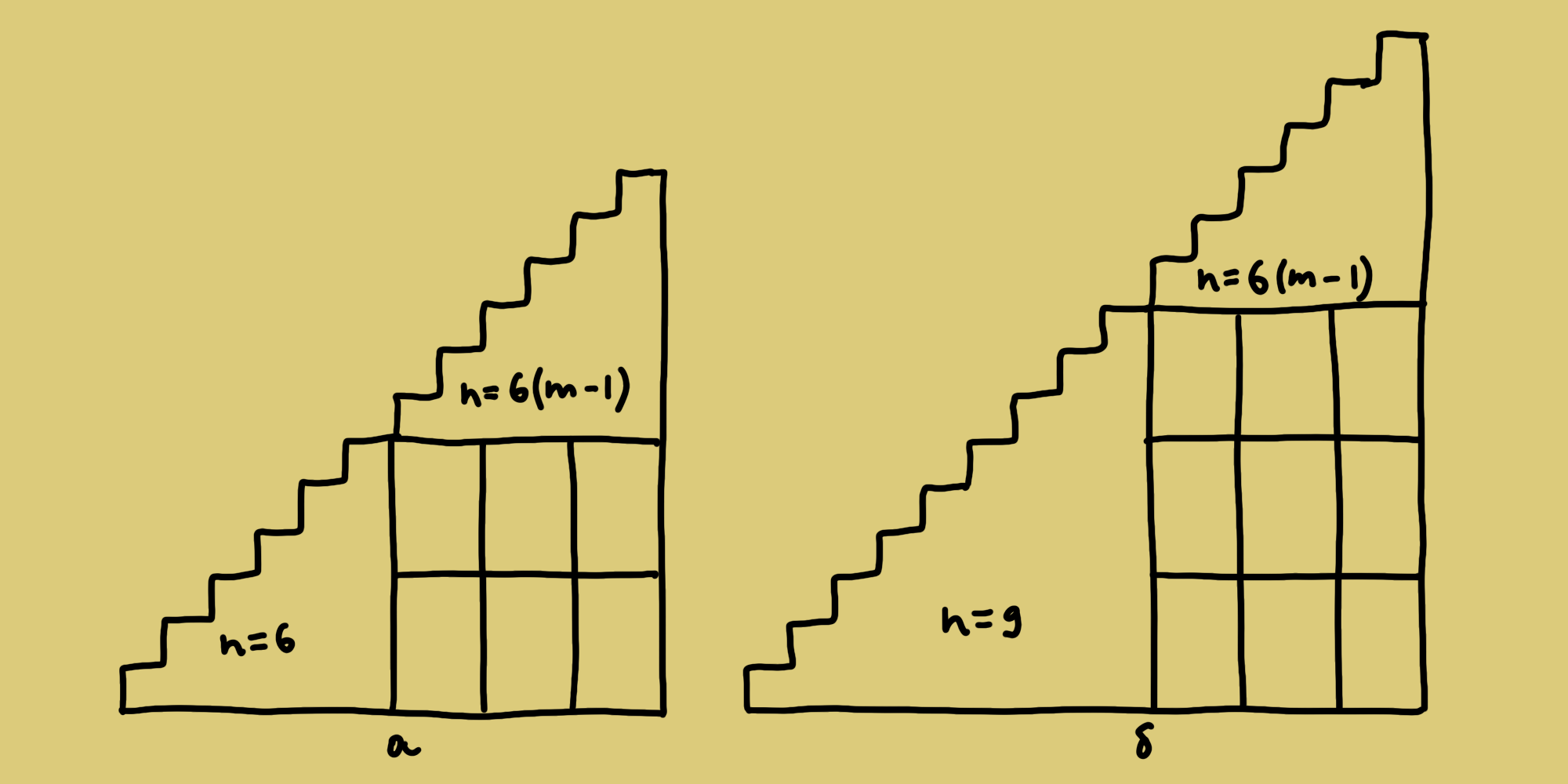
Наконец, если n = 3k + 2, k> 1, лестницу можно выложить из трех составляющих (см. рисунок):

• самой фигурки триминой, занимающей n = 2,
• прямоугольника 2 × 3k,
• фигуры лестницы, которая соответствует уже рассмотренному случаю 3k.

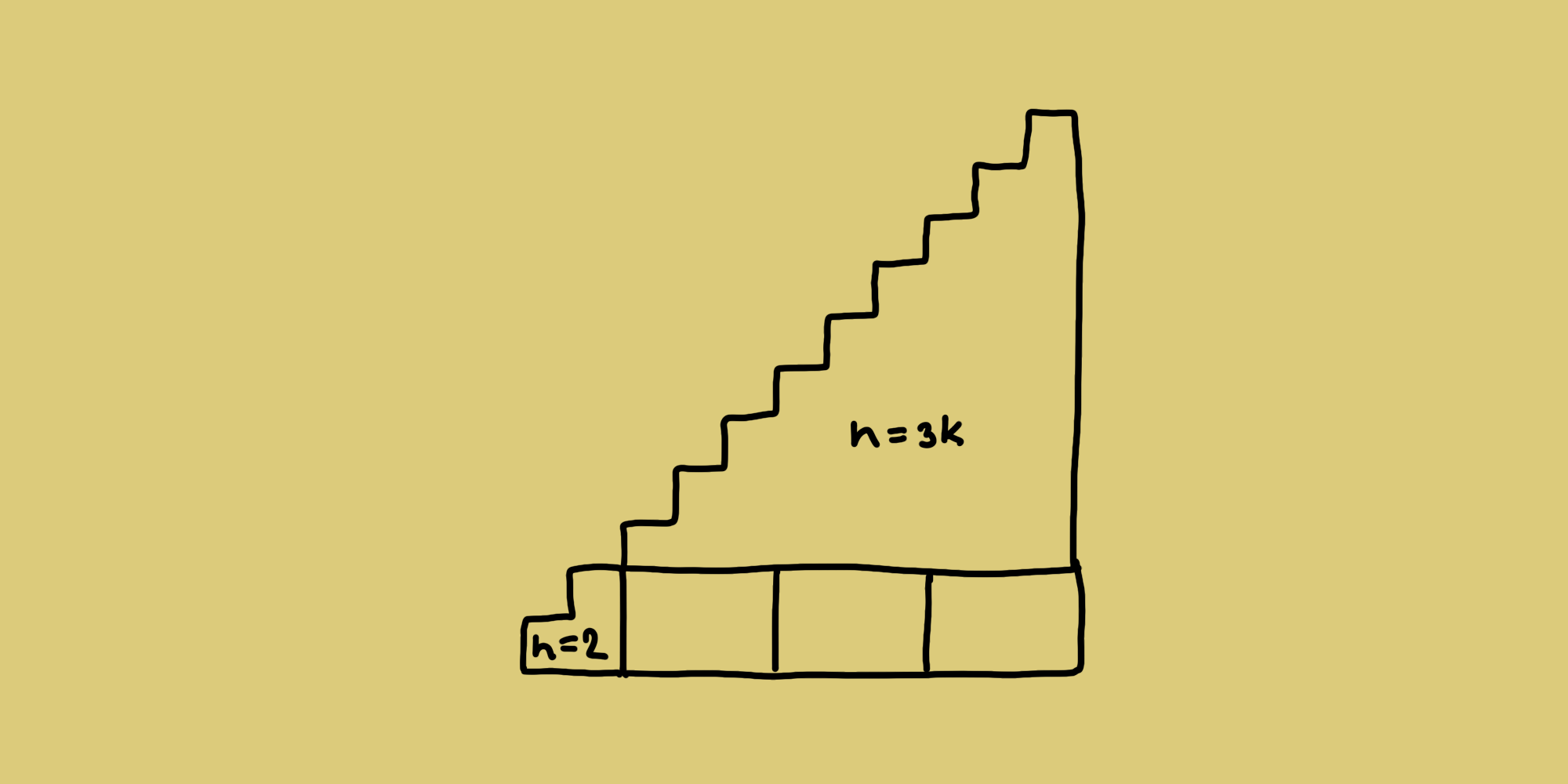
Таким образом, мы рассмотрели все варианты разрезания лестниц для любых n, подчиняющихся описанному в ответе условию.

Как решали задачу читатели Библиотеки программиста? Самым сложным для решающих задачу оказалось описать способ построения ряда. Сами решения были найдены. Правильную последовательность n привел пользователь krotbsod:

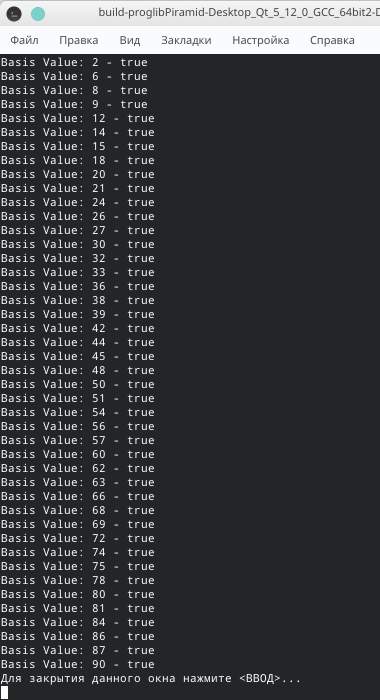
Примеры замощения для n = {2, 6, 8} привел пользователь riabininos:

Алгоритм описал пользователь kinshik:

Для начала представим все n в таблице с 6ю колонками, записав их последовательно. В первой строке 1,2,3,4,5,6. Во второй 7,8,9,10,11,12. И т.д. Для n=1 число клеток не делится на 3. Методом индукции можно убедиться, что, если для n число клеток пирамиды не делится на 3, то и для (n+3) число клеток не будет делиться на 3. Действительно, если к пирамиде для n добавить 3 ряда в основание, то число клеток всей пирамиды увеличится на число, делящееся на 3. В итоге результат не будет делится на 3. Из этого правила вытекает, что n в 1м и 4м столбцах не имеют решений. Легко убедиться, что нет решений для чисел 3 и 5, но есть решения для 2, 6, 9 и 11. Можно убедиться, что если есть решение для некоторого n, то есть решение для (n+6). Действительно, добавим к пирамиде для n в основание 6 рядов. Добавку можно разделить на 2 фигуры: пирамиду для 6 слева (которая имеет решение) и прямоугольник 6m. Очевидно, что эта вторая фигура хорошо делится на прямоугольники 2x3, которые имеют решение. Таблицу чисел, для которых могут быть найдены решения можно представить в виде: х 2 х х х 6 х 8 9 х 11 12 х 14 15 х 17 18 х 20 22 х 23 24 И т.д. Итого ответ: n=a+b*6, где a={2,6,9,11}, b={0,1,2,3,...}