pip install manim
    

        from manim import * 

class PointMovingOnShapes(Scene):
    def construct(self):
        square = Square(color=BLUE) # Cоздаем квадрат заданного цвета
        square.flip(RIGHT)
        square.rotate(-3 * TAU / 8) # Поворачиваем квадрат на -3/8 * 2*PI 

        # Проигрываем анимацию
        self.play(GrowFromCenter(square))
    

        $ manim -p -ql start.py PointMovingOnShapes
    

        $ manim -p -ql -i start.py PointMovingOnShapes
    

        from manim import * 

class PointMovingOnShapes(Scene):
    def construct(self):
        
        # Создаем квадрат
        square = Square(color=BLUE)
        square.flip(RIGHT)
        square.rotate(-3 * TAU / 8)
        
        # Создаем окружность
        circle = Circle()
        circle.set_fill(PINK, opacity=0.5) # устанавливаем цвет и прозрачность
      
        # Создаем анимации
        self.play(GrowFromCenter(square))
        self.play(Transform(square, circle))  # превращаем квадрат в круг
       
        self.wait() # ждем, чтобы картинка не сразу исчезала
    

        from manim import * 

config.background_color = DARK_GRAY
    

        class MovingFrame(Scene):
     def construct(self):
        # Пишем формулу
        equation = MathTex("2x^2-5x+2", "=", "(x-2)(2x-1)")

        # Создаем анимацию
        self.play(Write(equation))

        # Добавляем рамку
        framebox1 = SurroundingRectangle(equation[0], buff=.1)
        framebox2 = SurroundingRectangle(equation[2], buff=.1)

        # Создаем анимации
        self.play(Create(framebox1))  # создаем рамку

        self.wait()
        # replace frame 1 with frame 2
        self.play(ReplacementTransform(framebox1, framebox2))
    
        self.wait()
    

        class MathematicalEquation(Scene):
    def construct(self):
    
        # Пишем уравнения
        equation1 = MathTex("2x^2-5x+2")
        eq_sign_1 = MathTex("=")
        equation2 = MathTex("2x^2-4x-x+2")
        eq_sign_2 = MathTex("=")
        equation3 = MathTex("(x-2)(2x-1)")

        # Размещаем каждое уравнение и знак по своим местам
        equation1.next_to(eq_sign_1, LEFT)
        equation2.next_to(eq_sign_1, RIGHT)
        
        eq_sign_2.shift(DOWN)
        equation3.shift(DOWN)
        
        # ДВыравнеиваем уравнения по знаку равенства
        eq_sign_2.align_to(eq_sign_1, LEFT)
        equation3.align_to(equation2, LEFT)

        # Группируем уравнения
        eq_group = VGroup(equation1, eq_sign_1, equation2, eq_sign_2, equation3)

        # Создаем анимацию
        self.play(Write(eq_group))
        
        self.wait()
    

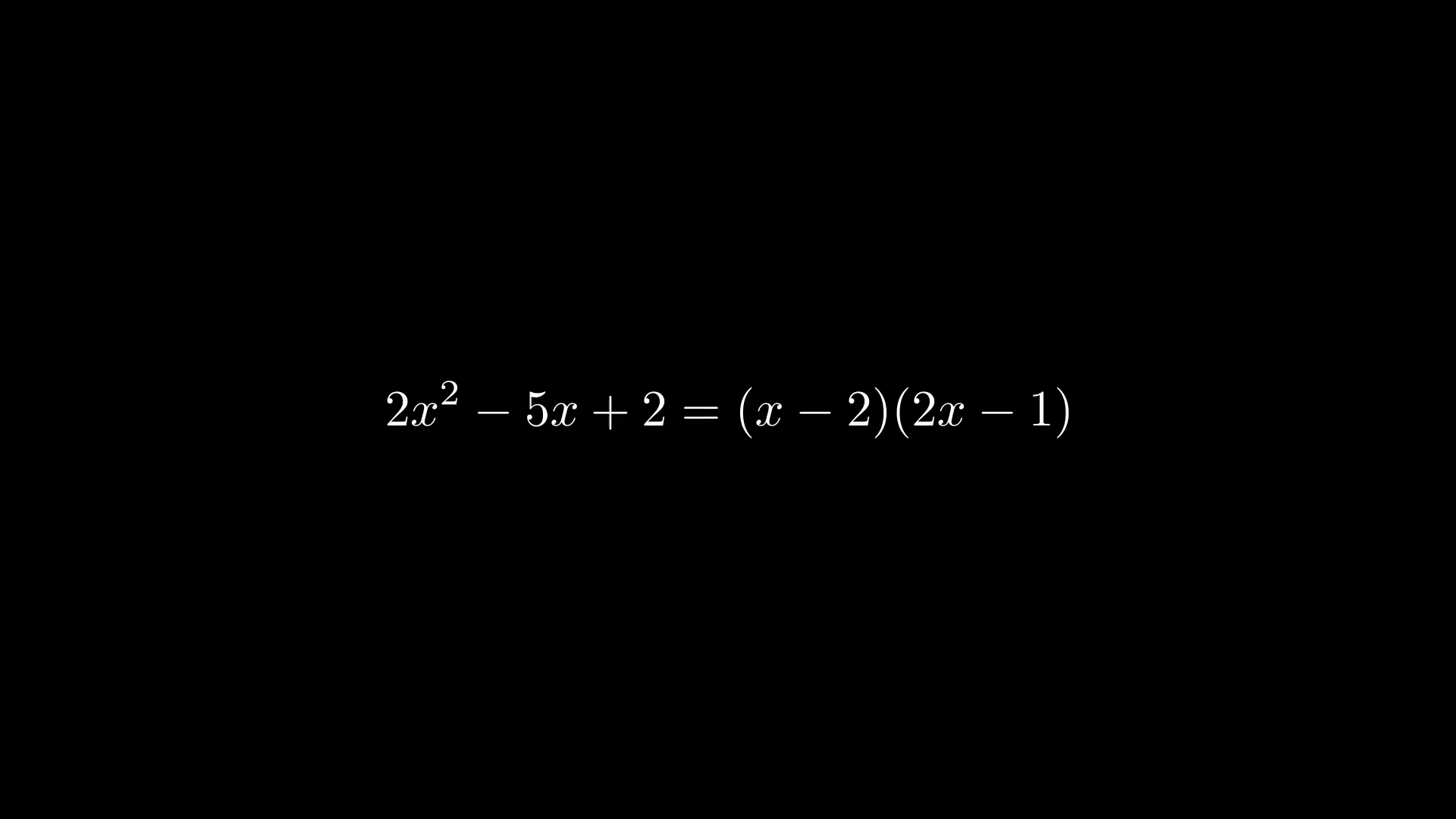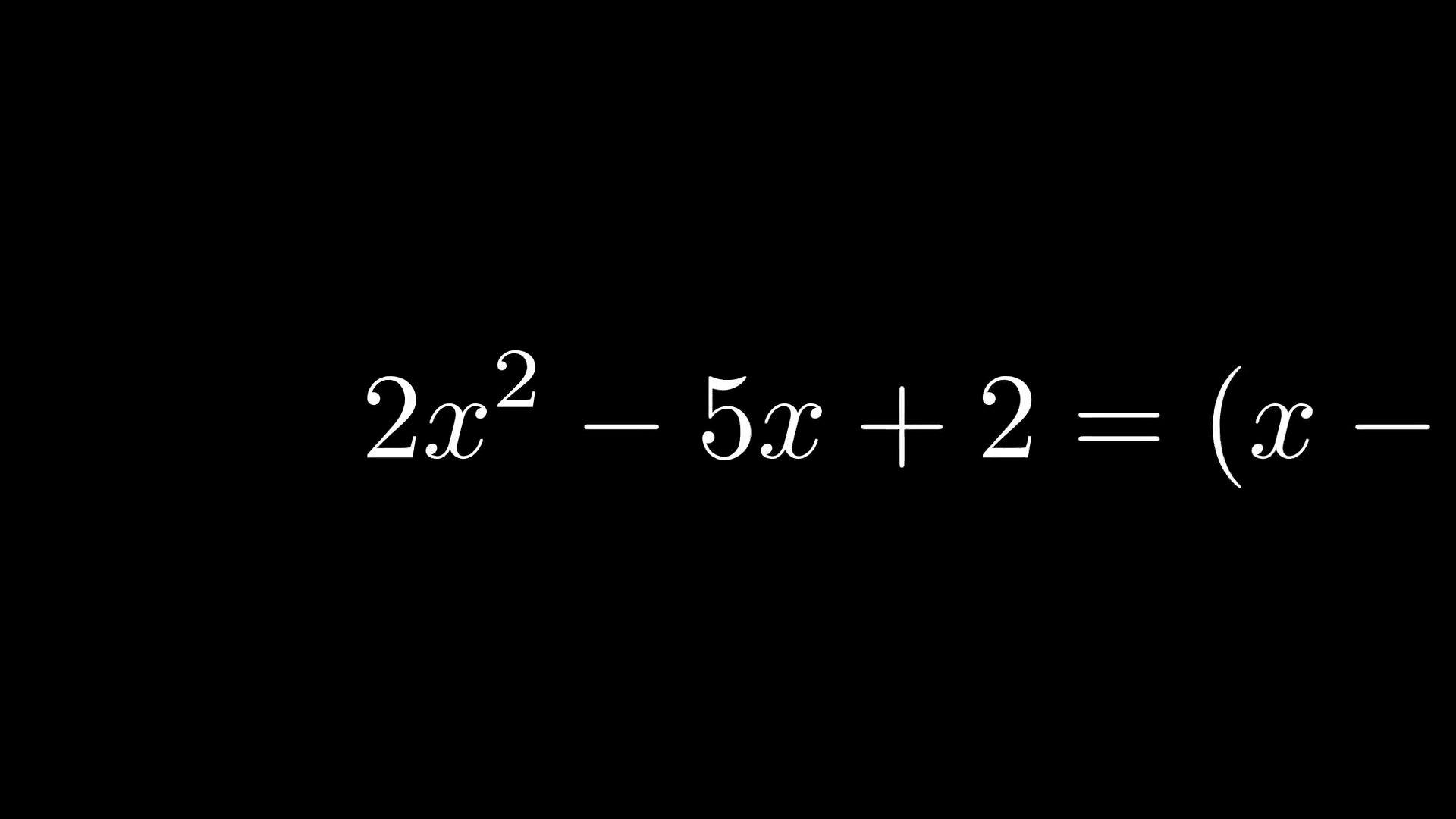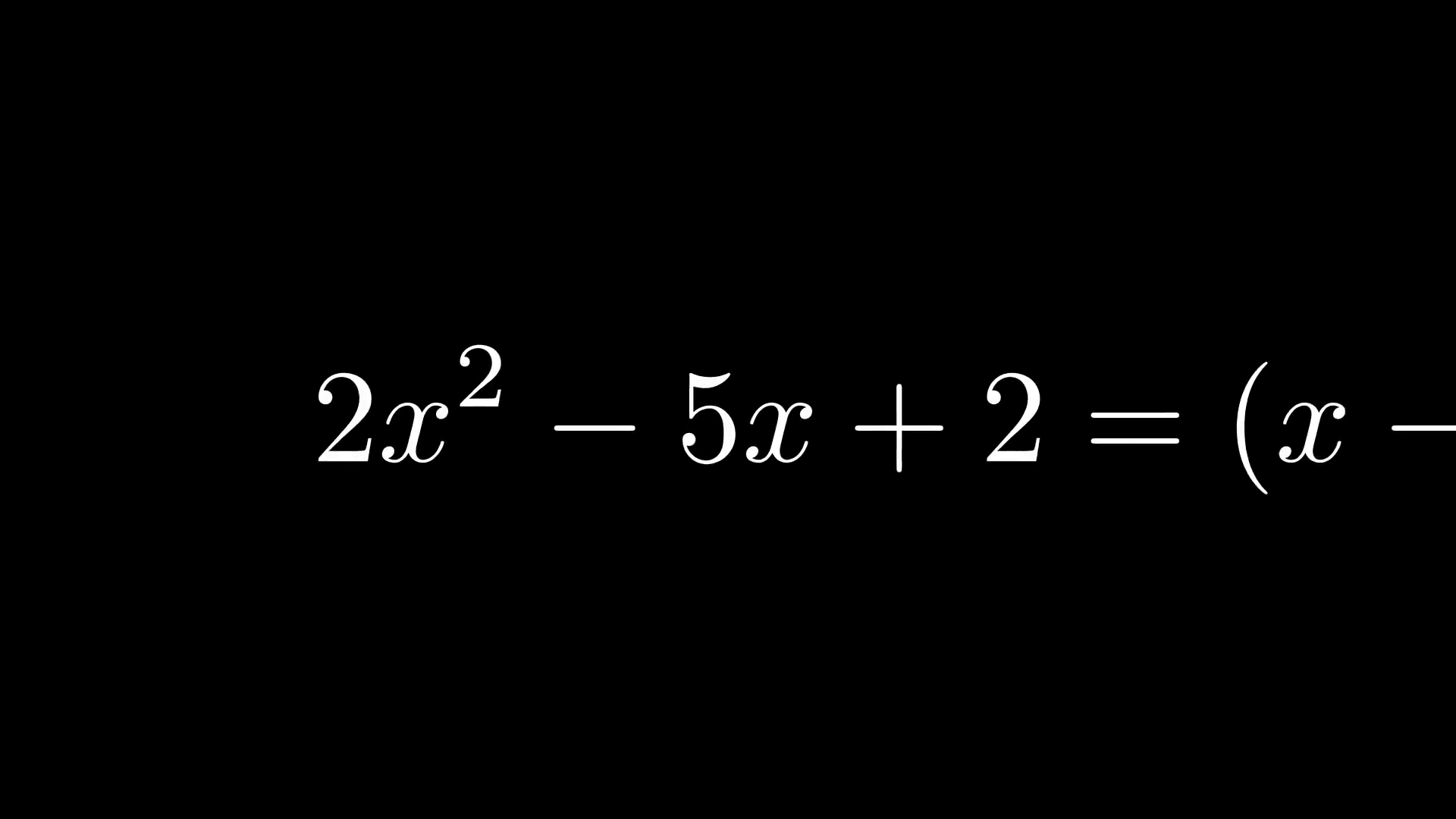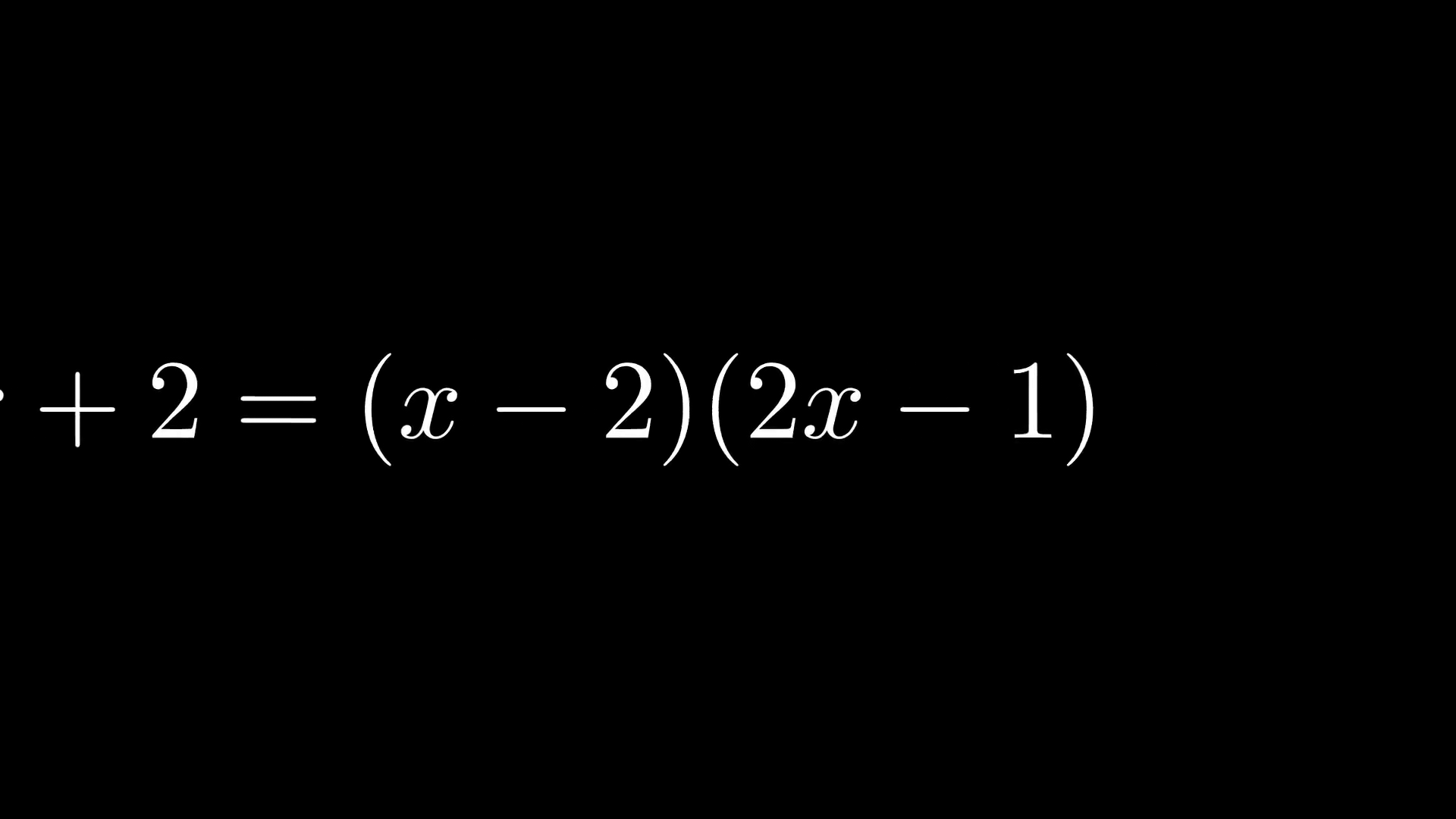
        class MovingAndZoomingCamera(MovingCameraScene):
    def construct(self):
        # Пишем уравнения
        equation = MathTex("2x^2-5x+2", "=", "(x-2)(2x-1)")

        self.add(equation)
        self.play(self.camera.frame.animate.move_to(equation[0]).set(width=equation[0].width*2))
        self.wait(0.3)
        self.play(self.camera.frame.animate.move_to(equation[2]).set(width=equation[2].width*2))

    

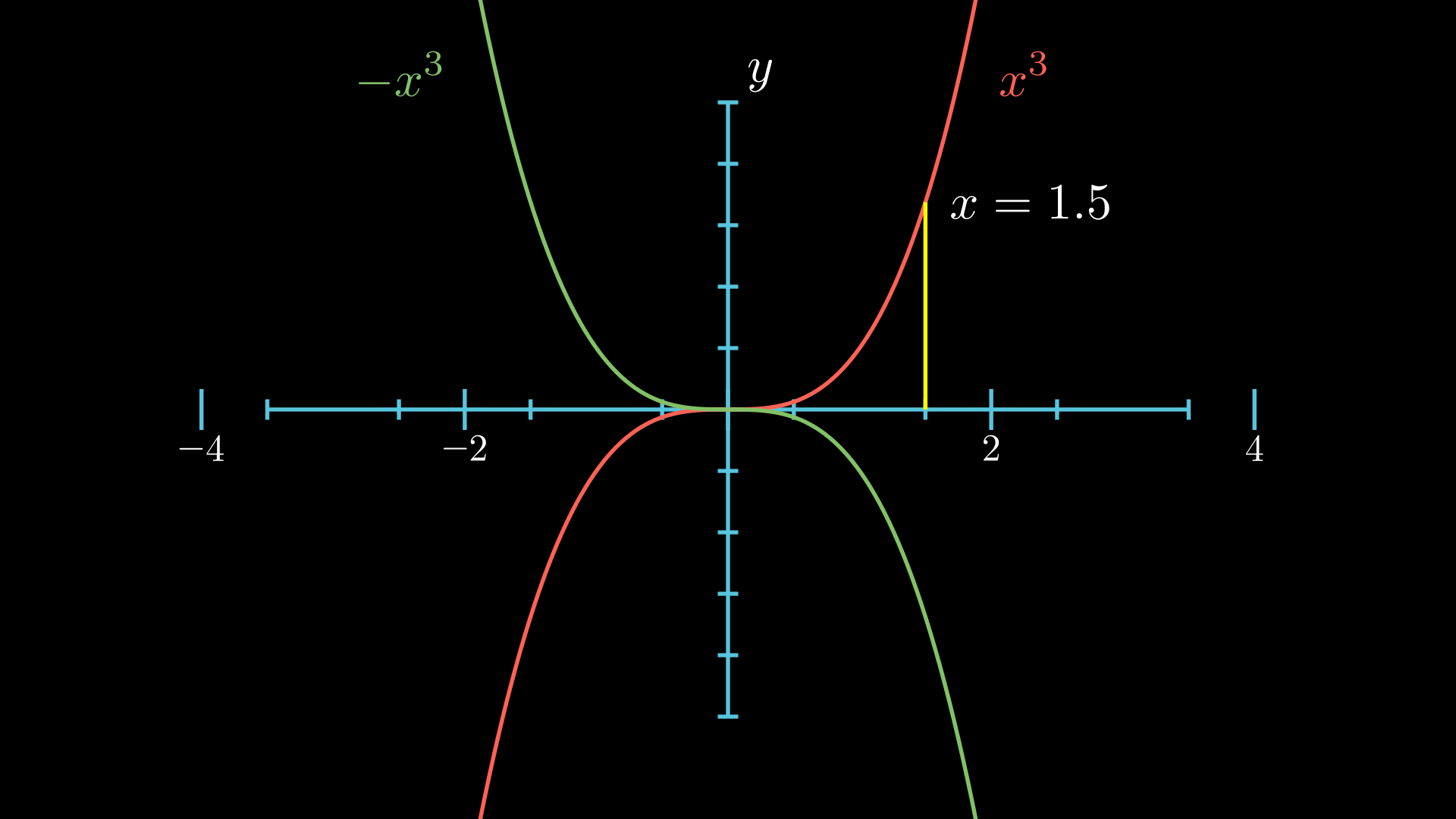
        class Graph(GraphScene):
    def __init__(self, **kwargs):
        GraphScene.__init__(
            self,
            x_min=-3.5,
            x_max=3.5,
            y_min=-5,
            y_max=5,
            graph_origin=ORIGIN,
            axes_color=BLUE,
            x_labeled_nums=range(-4, 4, 2), # x tickers
            y_labeled_nums=range(-5, 5, 2), # y tickers
            **kwargs
        )
    
    def construct(self):
        self.setup_axes(animate=False)

        # Рисуем графики
        func_graph_cube = self.get_graph(lambda x: x**3, RED)
        func_graph_ncube = self.get_graph(lambda x: -x**3, GREEN)

        # Создаем метки
        graph_lab = self.get_graph_label(func_graph_cube, label="x^3")
        graph_lab2 = self.get_graph_label(func_graph_ncube, label="-x^3", x_val=-3)

        # Добавляем вертикальную линию
        vert_line = self.get_vertical_line_to_graph(1.5, func_graph_cube, color=YELLOW)
        label_coord = self.input_to_graph_point(1.5, func_graph_cube)
        text = MathTex(r"x=1.5")
        text.next_to(label_coord)
       
        self.add(func_graph_cube, func_graph_ncube, graph_lab, graph_lab2, vert_line, text)
        self.wait()
    

        manim -p -qh -s more.py Graph
    

        def construct(self):
        self.setup_axes(animate=True)
        ################### Остальной код такой же ################### 
    

        manim -p -qh more.py Graph
    

        
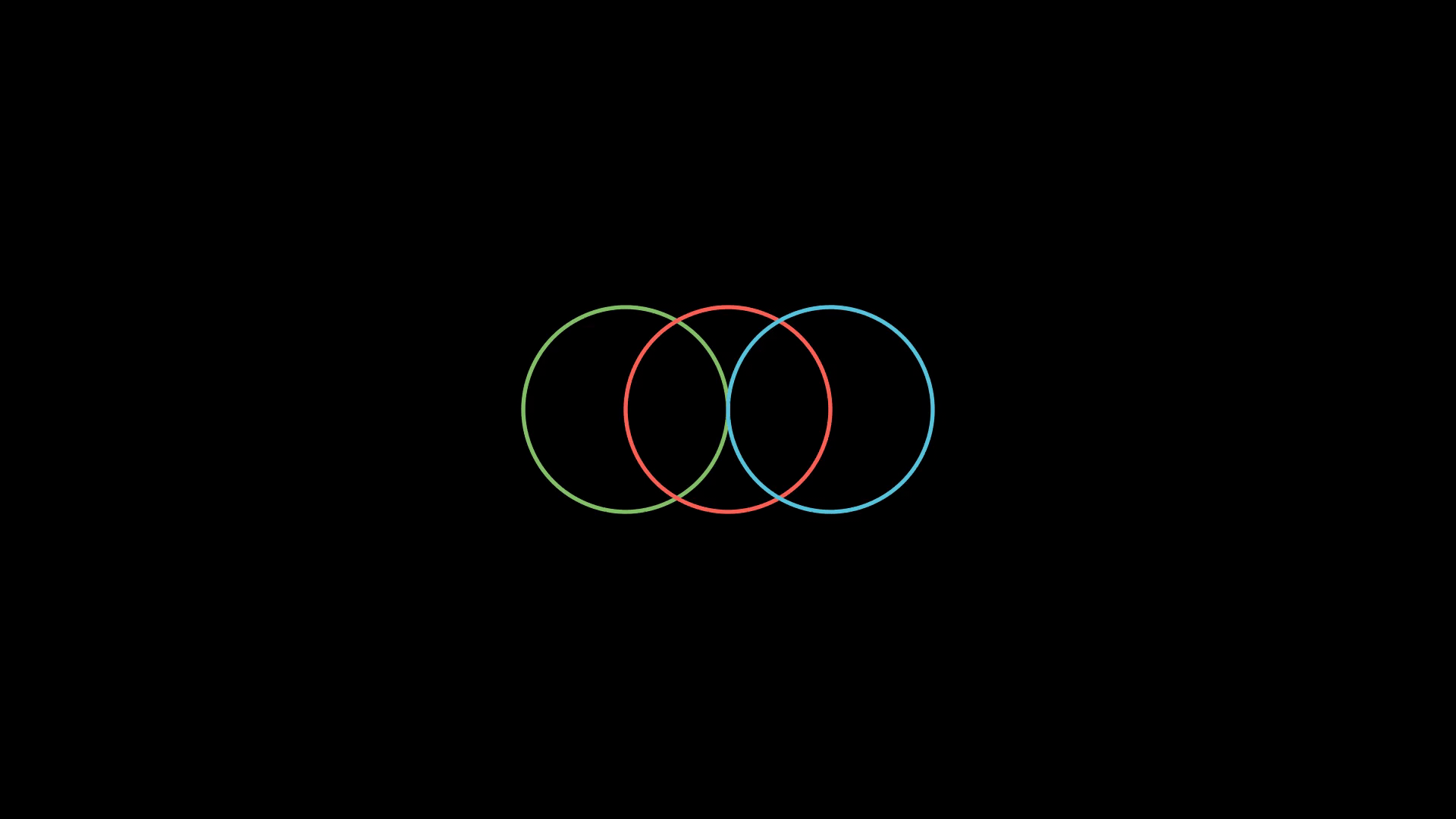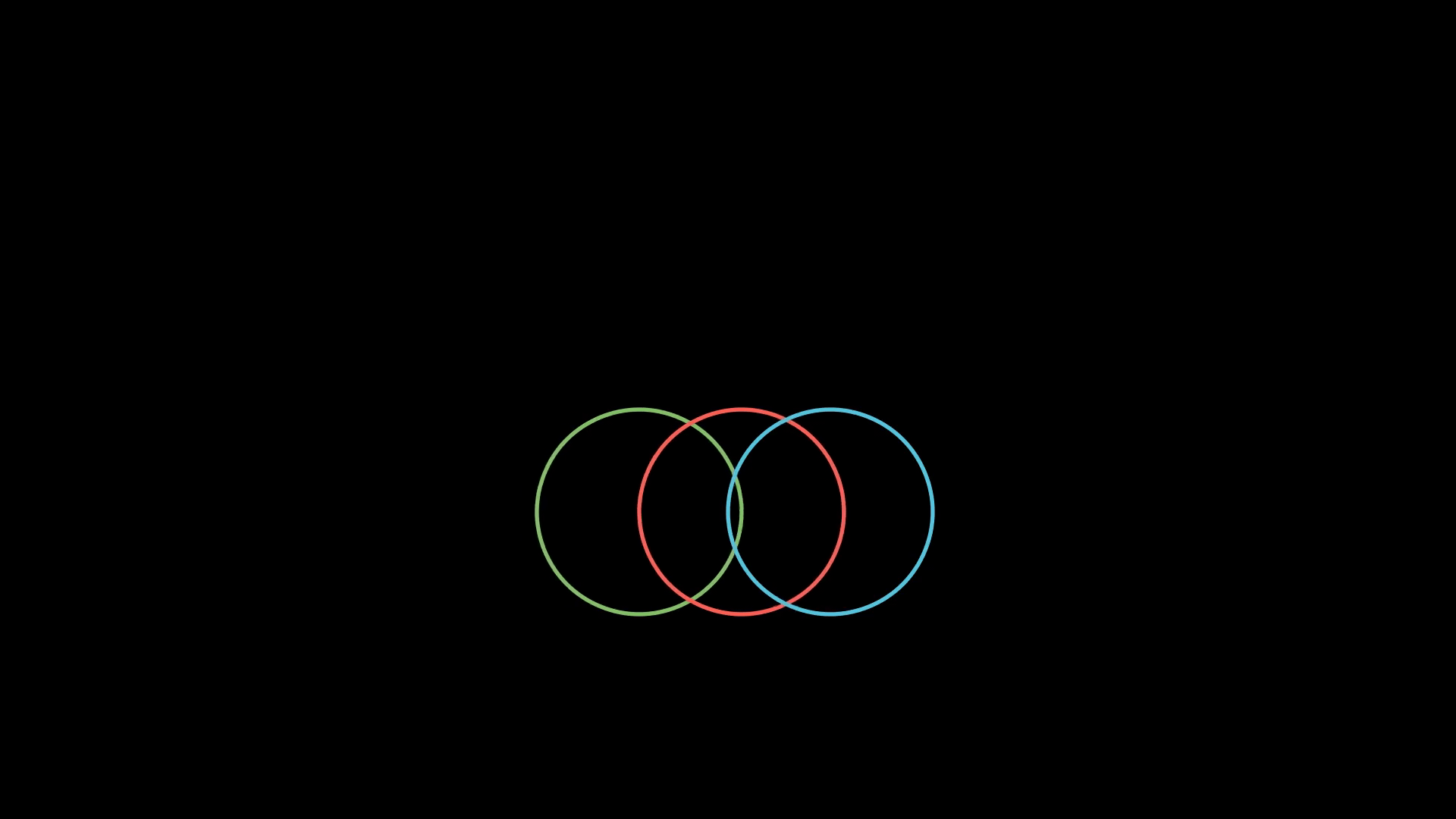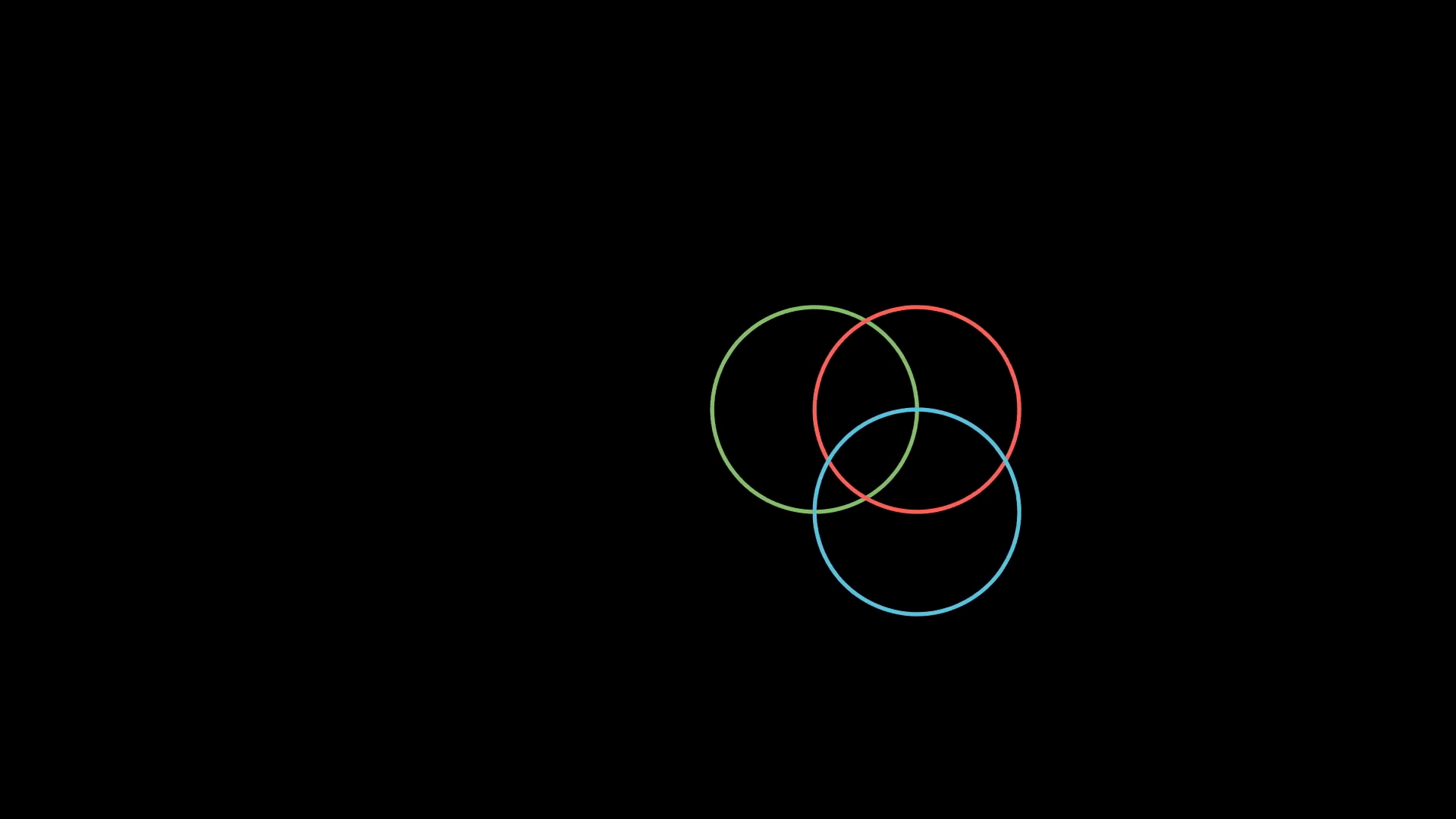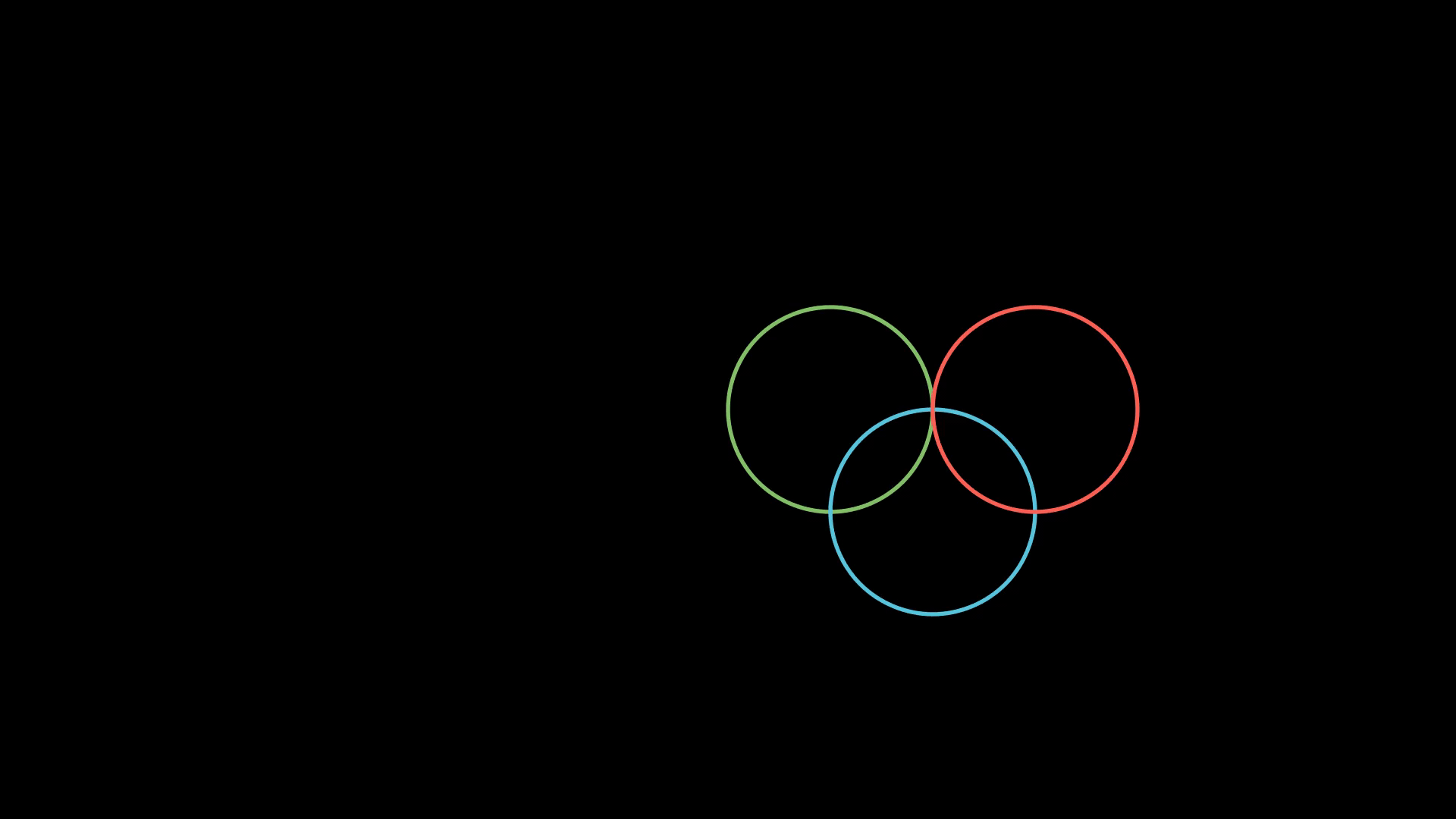
class GroupCircles(Scene):
    def construct(self):

        # Создаем круги
        circle_green = Circle(color=GREEN)
        circle_blue = Circle(color=BLUE)
        circle_red = Circle(color=RED)
        
        # Устанавливаем начальные позиции
        circle_green.shift(LEFT)
        circle_blue.shift(RIGHT)
        
        # Добавляем две группы
        gr = VGroup(circle_green, circle_red)
        gr2 = VGroup(circle_blue)
        self.add(gr, gr2) # добавляем группы на сцену
        self.wait()

        self.play((gr + gr2).animate.shift(DOWN)) # сдвигаем обе группы вниз
        
        self.play(gr.animate.shift(RIGHT)) # смещаем одну группу отдельно
        self.play(gr.animate.shift(UP))

        self.play((gr + gr2).animate.shift(RIGHT)) # сдвигаем две группы вправо
        self.play(circle_red.animate.shift(RIGHT))
        self.wait()
    

        class TracedPathExample(Scene):
    def construct(self):
        # Создаем окружность и точку
        circ = Circle(color=BLUE).shift(4*LEFT)
        dot = Dot(color=BLUE).move_to(circ.get_start())

        # Группируем точку и окружность
        rolling_circle = VGroup(circ, dot)
        trace = TracedPath(circ.get_start)

        rolling_circle.add_updater(lambda m: m.rotate(-0.3))  # Вращаем окружность

        self.add(trace, rolling_circle) # add trace and rolling circle to the scene

        # Сдвигаем окружность на 8 смещений вправо
        self.play(rolling_circle.animate.shift(8*RIGHT), run_time=4, rate_func=linear)