Прыг-прыг. Алгоритмическая головоломка о лягушках

Условие задачи

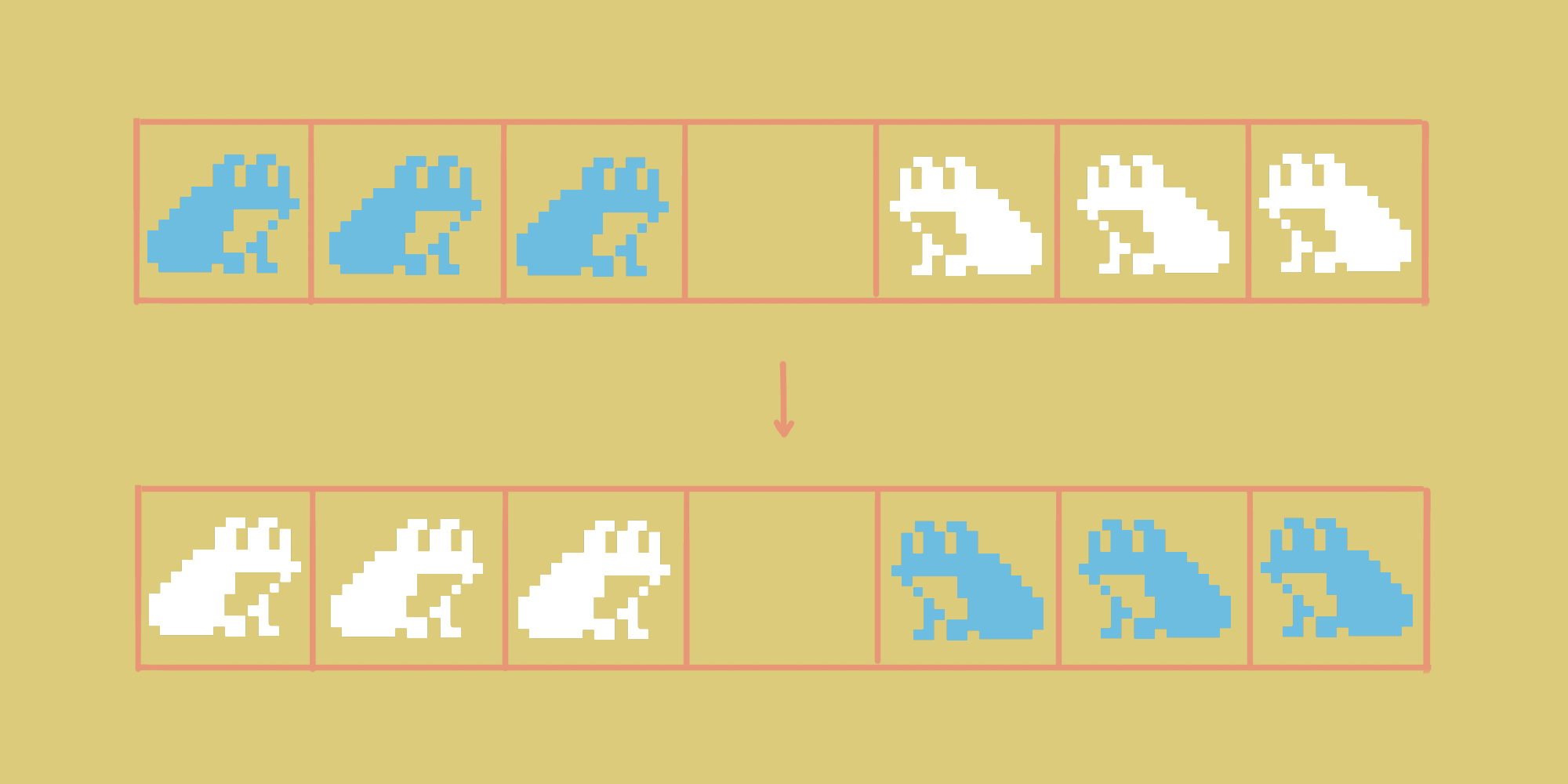
Как вы могли заметить по логотипу, Библиотеке программиста нравятся лягушки 🐸. Как настоящие (T), так и игрушечные (F). Однажды мы наблюдали такую сценку. На одномерной доске с 2n + 1 ячейками в первых n ячейках разместились n истинных лягушек в n первых ячейках и n лягушек-игрушек в последних n ячейках. По одной лягушке в ячейке, и ещё одна ячейка, разделяющая семейства. На рисунке показан случай для n = 3.

В рамках хода лягушка прыгает на пустую клетку. Напрямик или перепрыгнув через представителя противоположного семейства. Через своих сородичей лягушки одного типа не прыгают, это считается неуважительным. Трушные лягушки двигаются только вправо, фейковые – влево. Каждый тип может делать более одного хода подряд. В результате перепрыгиваний они хотят обменяться местами, как на картинке.

Вопрос: сколько ходов потребуется для 3 T и 3 F? Предложите алгоритм решения задачи.

Вопрос со звёздочкой 🌟: сколько ходов нужно для m T и n F, если m и n не равны?

Программное решение✨: попробуйте реализовать визуализацию решения для общего случая (из вопроса со звёздочкой) на любимом языке программирования. Напишите функцию, которая принимает на вход числа m и n, а возвращает число ходов, а также последовательность строк, содержащих T, F и пробел для пустой ячейки. Каждая строка соответствует одном ходу.

Решение – в следущей задаче.

Эта задача – четырнадцатый эпизод нашего сериала головоломок. После описания задачи идёт ответ на предыдущую – задачу о взломе банковского замка.

Решение задачи о взломе банковского замка

Ответ: 85.

Решение. Решим задачу в общем случае, то есть для любого числа n. Пронумеруем переключатели слева направо от 1 до n и обозначим состояния переключателя «включено» и «выключено» соответственно как 1 и 0. Чтобы помочь себе в решении общего случая головоломки, начнём с решения четырёх самых простых примеров.

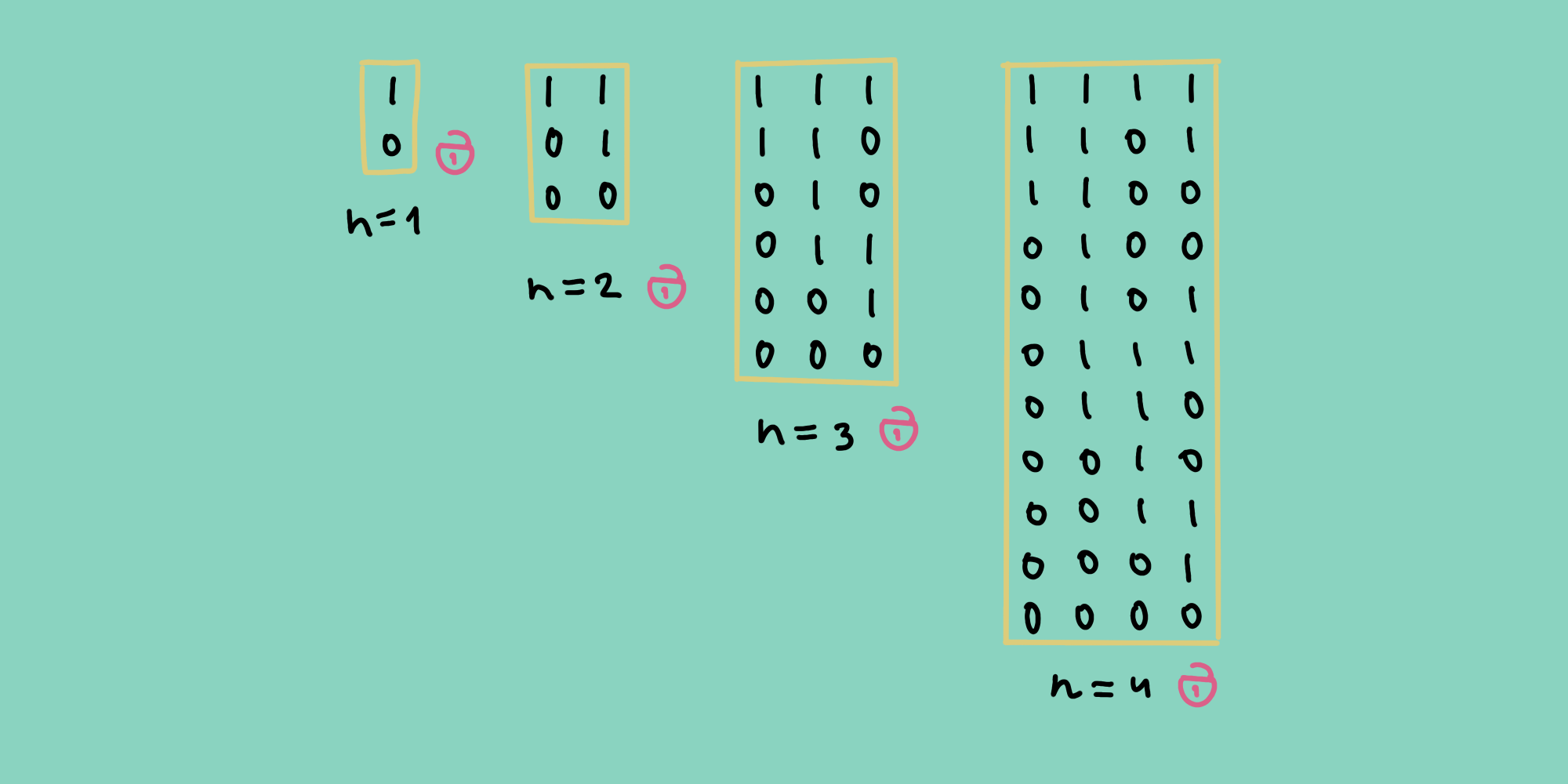
Теперь рассмотрим общий пример головоломки, когда исходная строка состоит из n единиц:

111, ... , 1.

Прежде чем мы сможем выключить самый левый переключатель, переключатели должны находиться в состоянии

110, ... , 0.

Следовательно, для начала нам нужно отключить последние n – 2 переключателей и сделать это за минимальное количество ходов. Другими словами, мы должны сначала решить ту же проблему, что и для последних n – 2 переключателей. Это может быть сделано рекурсивно с использованием решений для случаев n = 1 и n = 2.

После этого мы сможем переключить первый переключатель, чтобы получить

010, ... , 0.

Теперь, прежде чем мы сможем переключить второй переключатель, нам придётся пройти через такое состояние, при котором все переключатели, следующи за ним будут «вкл». Перевести все переключатели с третьего по последний на «вкл» можно, поменяв последовательность ходов, сделанных ранее, на обратную, чтобы переключить последние n – 2 переключателей из положения «вкл» в положение «выкл». Это даст нам

011, ... , 1.

Обозначим M(n) количеством переключений, сделанных алгоритмом. Получится следующее рекуррентное выражение:

или сокращённо:

Это выражение действует для n ≥ 3 , при этом известно, что M(1) = 1 , M(2) = 2. Решение рекуррентного уравнения по стандартной методике для линейных неоднородных рекуррентных уравнений второго порядка с постоянными коэффициентами даёт следующий необычный результат:

Для чётных n данная формула сводится к

Для нечётных:

Действительно: если n = 7, то M(n) = 85.

Как ответили читатели Библиотеки программиста? Алгоритмические ответы с указанием рекуррентных соотношений дали читатели lasangqwerty и maximzombi:

f(n) = f(n-1) + 2*f(n-2) + 1, f(7) = 85

Посчитаем ответ для случая с 1 и 2 тумблерами: f(1)=1 f(2) = 2 Пусть тумблеров n штук. Чтобы выключить самый левый, нужно, чтобы (n-1)-ый тумблер слева остался вкл, а остальные выкл. Чтобы выключить n-2 левых, нужно f(n-2) переключений. Также нужно переключить сам левый тумблер (т.е. еще одно переключение). Итого этими действиями мы привели тумблеры к виду: 0100...00, где 1 – вкл, 0 – выкл Чтобы выключить (n-1)-й тумблей, нужно включить все тумблеры правее него(т.е. нужно включить только (n-2)-й тумблер, но для его включения нужно включить (n-3)-й тумблей и т.д.). Чтобы включить все тумблеры правее (n-1)-го, необходимо также f(n-2) действий. Теперь тумблеры имеют вид 0111...11 Осталось перевести все тумблеры левее самого левого в режим выкл., на что понадобится f(n-1) действий. Итого получаем рекуррентную формулу: f(1)=1, f(2)=2, f(n)=f(n-2) * 2 + f(n-1) + 1 => f(7) = 85

Читатель wil4 привёл саму последовательность переключений:

1111111 1111110 1111010 1111011 1111001 1111000 1101000 1101001 1101011 1101010 1101110 1101111 1101101 1101100 1100100 1100101 1100111 1100110 1100010 1100011 1100001 1100000 0100000 0100001 0100011 0100010 0100110 0100111 0100101 0100100 0101100 0101101 0101111 0101110 0101010 0101011 0101001 0101000 0111000 0111001 0111011 0111010 0111110 0111111 0111101 0111100 0110100 0110101 0110111 0110110 0110010 0110011 0110001 0110000 0010000 0010001 0010011 0010010 0010110 0010111 0010101 0010100 0011100 0011101 0011111 0011110 0011010 0011011 0011001 0011000 0001000 0001001 0001011 0001010 0001110 0001111 0001101 0001100 0000100 0000101 0000111 0000110 0000010 0000011 0000001 0000000

Также задача подробно обсуждалась в нашем сообществе вк, там вы можете увидеть много различных подходов, в том числе ручной перебор и программные решения. Первым точное решение привёл Сергей Семёнов.

85, рекуррентно, для включения четного тумблера надо повторить все предыдущие переключения, для нечетного еще одно, a(2n) = 2*a(2n-1), a(2n+1) = 2*a(2n)+1